What is the end of numbers
Number System - Definition, Types, Conversion, Examples, Facts
What Are Numbers?
A number is an arithmetic value used to represent quantity. Hence, a number is a mathematical concept used to count, measure, and label. Thus, numbers form the basis of mathematics.
For example, this is 1 butterfly and these are 4 butterflies.
Related Games
History of Numbers
The inscriptions found at archaeological sites show that early humans used various symbols to show numbers. For example, ancient farmers, traders, and merchants used tally marks to show quantities. In tally marks, a standing line is drawn for each count and the fifth count is shown by striking off the four lines. This, however, was a tedious way and it was not feasible to show quantities.
Different ways of writing numbers were brought to use with the development of early civilizations. They used different symbols to show larger quantities. But even with these systems, it was not easy to show large quantities.
Around the seventh century, a decimal (or base ten) positional method, was perfected in India. This method used ten unique symbols to represent any number or quantity. These symbols are 0, 1, 2, 3, 4, 5 6, 7, 8, and 9.
This system was spread across Europe by the Arab merchants, scholars, and conquerors.
This system is called the Hindu–Arabic numeral system, and it remains the most common system for representing numbers to date.
Related Worksheets
Numbers in Everyday Life
Numbers are used everywhere around us. Your birthday has numbers that tell the day, month, and year you were born.
Numbers are used to keep track of time. We use clocks that show us time. We plan our day and events according to time.
Numbers are involved in buying and selling too. To count money and the units of an item, we use numbers.
Numbers are used for measurement. Temperature, weight, length, capacity, speed, distance, area, volume, and so on are measured using numbers.
Numbers play an important role in our body too. We have 2 eyes, 2 ears, 1 nose, 2 hands, 2 legs, and an adult body has 206 bones.
Our houses have numbers, bank accounts have numbers, and so do our cars, buses, trains, and flights.
Number Representation
- Digits 0-9
A number system is a writing system for denoting numbers using digits or symbols in a logical manner.
We use the digits from 0 to 9 to form all other numbers.
With the help of these digits, we can create infinite numbers.
For example, 121; 34,987; 2,987,633; 459,227,904; …
This number system using 10 digits is called the Decimal Number System.
- Alphabetical Form of Number
Number words are the alphabetical form of numbers. As the name suggests, these are numbers written in words.
For example:
1 One
2 Two
15 Fifteen
33 Thirty-three
- Symbolically, Using Numerals
Numerical symbols are numerals, such as Hindu-Arabic numerals (for example: 112, 415, 999) or Roman numerals (I, II, V, VIII).
Cardinal Numbers and Ordinal Numbers
Cardinal numbers are counting numbers. The numbers that we use for counting are called cardinal numbers.
Cardinal numbers tell us how many things, items, or objects are there.
Example: 1, 2, 3, 10, 158
Ordinal numbers give us the exact position of a thing, item, or an object in the list. Ordinal numbers tell the position of an object rather than its quantity.
Example: 1st, 2nd, 3rd, 9th, 150th
Types of Numbers
Apart from the above, there exist other numbers, namely even and odd numbers, prime numbers, and composite numbers. These can be defined as follows:
Fraction and Decimal Numbers:
Solved Examples on Numbers
Example 1: Classify the given set of numbers as fractions or decimals.
7/12; 0.0008; 1.52; 100/10; 4 1/2; 7555.0
Solution:
Example 2: Write the numerator and denominator of given rational numbers.
- 17/21 (b) 4/5 (c) 25/22
Solution:
Example 3: Write the numbers in words.
- 548
- 1,660
Solution:
- Five hundred and forty-eight.
- One thousand six hundred and sixty.
Practice Problems
1
How many odd numbers are there between 64 and 90?
11
12
13
14
Correct answer is: 13
65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89
2
Sum of the numbers of primes between 10 to 20 and 30 to 40 is
5
6
7
8
Correct answer is: 6
Prime numbers between 10 to 20 are 11, 13, 17 and 19 So, there are 4 prime numbers between 10 to 20. Prime numbers between 30 to 40 are 31 and 37 So, there are 2 prime numbers between 30 to 40.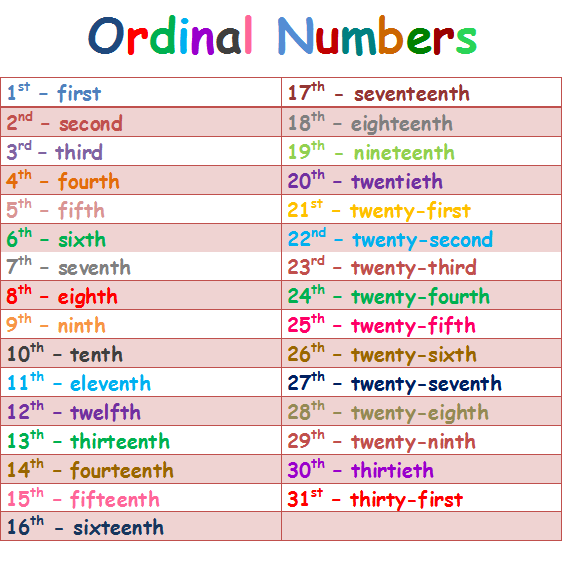
Sum = 4 + 2 = 6
3
Four thousand eight hundred and eight in numeral form is written as:
4,880
4,808
4,800
48,008
Correct answer is: 4,808
4,000 + 800 + 8 = 4,808
4
What type of number is –5?
Natural number
Whole number
Integer
Correct answer is: Integer
–5 is a negative number, so it’s an integer.
Frequently Asked Questions
How do you find if a number is odd or even?
If a number is divisible by 2 with no remainder, then it is an even number. If a number is divided by 2 and leaves the remainder 1, then it is an odd number.
Is zero an even number?
When zero is divided by 2, the quotient is 0 and remainder is also 0. So, zero is an even number.
Can rational numbers be negative?
Yes, rational numbers are classified as positive, zero, or negative rational numbers.
Do fractions count as whole numbers?
Whole numbers do not include fractions or decimals.
Last digits are changed to zeros when you type long numbers in cells of Excel - Office
Twitter LinkedIn Facebook Email
- Article
- 2 minutes to read
-
- Applies to:
- Excel 2013, Excel 2010, Microsoft Office Excel 2007, Microsoft Office Excel 2003
Symptoms
When you type a number that contains more than 15 digits in a cell in Microsoft Excel, Excel changes any digits past the fifteenth place to zeros.
For example, you type a credit card ID number in the following format:
####-####-####-####
In this situation, Excel changes the last digit to a zero.
Cause
Excel follows the IEEE 754 specification for how to store and calculate floating-point numbers. Excel therefore stores only 15 significant digits in a number and changes digits after the fifteenth place to zeros
Workaround
Add a quotation mark
To prevents digits from being changed to zero, type a single quotation mark before you enter the number.
To do this, select a blank cell, type a single quotation mark ('), and then enter the number. All digits are displayed in the cell.
Format the cells
To avoid having to type a quotation mark in every affected cell, you can format the cells as text before you enter any data.
Select all the affected cells, and then press Ctrl+1 to open the Format Cells dialog box.
On the Number tab, select Text from the Category list, and then select OK.
This behavior occurs only if the cell is formatted as Number, and the number that is entered exceeds 15 digits. For cells that are formatted as text, you can type up to 32,767 characters. Excel displays up to 1,024 characters on the worksheet.
Because custom number formats are designed to work primarily with numbers, you cannot create a custom number format that stores more than 15 digits. For example, you cannot use the following format to store a 16-character credit card ID as a number:
####-####-####-####
However, if you type the number in the cell that is formatted as text, all the characters remain as you type them because Excel stores the number as text and not as a number.
Still need help? Go to Microsoft Community.
Signs of divisibility of numbers by 2, 3, 5, 9, 10
Let's help you understand and fall in love with mathematics
Start learning
126.
9K
The sign of divisibility is an algorithm that helps you quickly determine whether a number is a multiple of a predetermined number. Let's consider algorithms for numbers from 1 to 10.
The concept of divisibility
Signs of divisibility of numbers are features of numbers that allow you to determine whether a number is a multiple of a divisor or not.
Divisibility properties:
-
All whole numbers are divisible by one.
-
Each non-zero integer is divisible by a natural number equal to the modulus of the given integer.
-
All natural numbers are zero divisors.
-
If the integer a is divisible by the natural number b and the absolute value of a is less than b , then a is equal to zero.
-
If the integer is a is different from zero and is divisible by the natural number b , then the absolute value of a is not less than b .
-
The only divisor of the unit is the unit itself.
-
For the integer a to be divisible by the natural number b , it is necessary and sufficient that the modulus of the number a is divisible by b .
-
If natural numbers are divisible by each other without a remainder, then they are equal.
Divisibility properties can be used to solve problems and prove theorems.
Even numbers are numbers that are divisible by two: 0, 2, 4, 6, 8, 10, 12, etc.
Zero is also an even number.
Odd numbers are numbers that are not divisible by two: 1, 3, 5, 7, 9, 11, 13, etc.
Solve math homework for 5.
the most difficult topic.
Signs of divisibility
Consider the criteria for divisibility by 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. is divisible by 2 if its last digit is even.
Example: 2164 is divisible by 2 because the last digit (6) is even.
Signs of divisibility by 3
Only those numbers whose sum of digits is divisible by 3 are divisible by 3.
Example: the number 81 300 is divisible by 3, since the sum of its digits is 8 + 1 + 3 + 0 + 0 = 12 divisible by 3.
Conditions for divisibility by 4
A number is divisible by 4 if its last two digits are zeros or form a number that is divisible by 4.
Examples:
-
The number 37,100 is divisible by 4 because it ends in two zeros ;
-
7524 is divisible by 4 because the last two digits (24) are divisible by 4.
Conditions for divisibility by 5
Numbers that end in 0 or 5 are divisible by 5.
Example: 450 is divisible by 5 because the last digit is 0.
Signs of divisibility by 6
A number is divisible by 6 if it is divisible by 2 and 3 at the same time.
861 is not divisible by 6 because it is divisible by 3 but not by 2.
Signs of divisibility by 7
Divisibility by the number 7 can be checked as follows:
-
Multiply the last digit of the number by two.
-
Subtract the resulting product from the remaining number (without the last digit).
-
The resulting difference must be a multiple of 7.
Example: the number 343 is divisible by 7, since 34 − (2 3) = 28, and 28 is divisible by 7.
form a number that is divisible by 8.
Example:
-
the number 11,000 is divisible by 8 because it ends in three zeros;
-
12128 is divisible by 8 because the last three digits form the number (128) which is divisible by 8.
Signs of divisibility by 9
Only those numbers whose sum of digits is divisible by 9 are divisible by 9.
Example: the number 2637 is divisible by 9, since the sum of its digits 2 + 6 + 3 + 7 = 18 is divisible by 9
Conditions for divisibility by 10
Divisible by 10 are those numbers that end in zero or several zeros.
Example:
-
980 is divisible by 10;
-
462 is not divisible by 10 - last digit is 2.
Mathematics courses will help you improve your grades, prepare for tests, VLOOKUP and exams.
Math cheat sheets for parents
All math formulas at hand
Lidiya Kazantseva
Skysmart author
Previous article
411.2K
0003
To the next article
105.5K
2 Simple and composite numbers
Get a training plan that will help to understand and love mathematics
in an introductory lesson with methodologist
-
We will identify knowledge gaps and give tips on training
-
Let's tell you how the classes are going
-
Let's choose the course
Signs of divisibility by 11,12,13,14,15.
Examples of problem solving. - Alpha school
- Articles
- Divisibility criteria (Part 2)
Divisibility by \(11\)
A number is divisible by \(11\) if the difference between all digits in odd places and digits in even places is divisible by \(11\).
Task 1 . Check divisibility of numbers by \(11\): \(2547039\), \(13165648\) .
Solution. Let's find the sum of digits in even and odd places of the number \(2547039\).
- \((9+0+4+2)-(3+7+5)=15-15=0-\) divided by 11.
- \((8+6+6+3)-(4+5+1+1)=23-11=12-\) is not divisible by 11
Sign of divisibility by \(12\)
A number is divisible by 12 if it is a multiple of \(3\) and \(4.
\)
Problem 2 . Check the divisibility of numbers by \(12\): \(9012\) and \(23988\).
- \(9012\)is divisible by \(3:\) \(9+0+1+2=\frac{12}{3}=4\) and the last two digits are divisible by \( 4:\frac{12}{4}=3\).
- \(23988\) sum of digits is divisible by \(3:2+3+9+8+8=\frac{30}{3}=10\) and the last two digits are divisible by \(4:\frac{88 }{4}=22.\). Output: numbers \(9012\) and \(23988\) are divisible by 12.
Sign of divisibility by \(13\)
A number is divisible by \(13\) if the number of its tens is multiplied by \(4\) and added to the remaining digits, a multiple of \(13\).
Task 3 . Check the divisibility of numbers by \(13\): \(845\) and \(676\).
- \(84+(4*5)=104 -\) is divisible by \(13\).
- \(67+(4*6)=67+24=91-\) is divisible by 13.
Answer: the numbers \(845,676\) are divisible by 13.
Divisibility by \(14\)
A number is divisible by \(14\) if and only if it is divisible by \(2\) and \(7\).
Let's consider the number \(994:\) the record of the number ends with an even digit, hence the test of divisibility by \(2\) is fulfilled.
Check divisibility by \(7:\) \(99-2*4=99-8=91.\)
Repeat the steps: \(9-2*1=7-\) is divisible by \(7\ ). \(994\) is divisible by \(14\).
Sign of divisibility by \(15\)
A number is divisible by \(15\) if it is divisible by \(3\) and \(5\).
Consider the number \(6375.\) The number \(6375\) is divisible by \(3\) since the sum of its digits is a multiple of \(3\). Also, this number is divisible by \(5\), because the last place is five. The number \(6375\) is divisible by \(15\).
Sign of divisibility by \(17\)
A number is divisible by \(17\) if the number of its tens is multiplied by \(12\) and added to the remaining digits, a multiple of \(17\).
Task 4 . Determine if the number \(29053\) is a multiple of seventeen.
Solution.
\(2905+36=2941\)→\(294+12=306\)→\(30+72=102\)→\(10+24=34\).
\(29053\) is divisible by \(17\).
Sign of divisibility by \(19\)
A number is divisible by \(19\) if twice its tens are added to the remaining digits, a multiple of \(19.\)
Example: \(646\) is divisible by \(19\), because \(64+( 6*2)=76\) is divisible by \(19\).
Sign of divisibility by \(23\)
A number is divisible by \(23\) if three times its hundreds are added to the remaining digits, a multiple of \(23\).
Example: \(28842-288+(3*42)=414\). Repeat the steps: \(4+(3*14)=46\), \(46\) is divided by \(23\), hence \(28842\) is a multiple of \(23\).
Sign of divisibility by \(25\)
A number is divisible by \(25\) if its last two digits are divisible by \(25\), that is, if its last digits end in \(00,25,50\) or \(75\) or if the number is a multiple of \( 5\).
Sign up for a free trial lesson here and figure out what you don't understand.
More lessons and assignments in mathematics with the teachers of our online school "Alpha". Sign up for a trial lesson now!
Sign up for a free knowledge test!
By clicking the "Sign up" button, I accept the terms of the User Agreement and Privacy Policy
Our teachers
Raisa Stepanovna Verenich
Math tutor
Experience (years)
Education:
Odessa National Mechnikov University
Conducted classes:
Form of study:
Remote (Skype)
Yuri Alekseevich Alekseenko
Math tutor
Experience (years)
Education:
Kuban State University
Conducted classes:
Form of study:
Remote (Skype)
Svetlana Alekseevna Sazonova
Math tutor
Experience (years)
Education:
Ryazan State Pedagogical University.
S.A. Yesenina
Conducted classes:
Form of study:
Remote (Skype)
Items
- Mathematics
- Physics Tutor
- Chemistry Tutor
- Russian language tutor
- English tutor
- social studies tutor
- Russian history tutor
- biology tutor
- Geography Tutor
- Computer science tutor
Specializations
- Preparation for the OGE in mathematics
- Geometry tutor
- Preparing for the Unified State Examination in Mathematics (profile level)
- English tutor for adults
- English speaking tutor
- VLOOKUP in mathematics
- Tutor for preparing for the exam in social studies
- Tutor for preparing for the OGE in social studies
- Informatics tutor to prepare for the OGE
- Informatics tutor to prepare for the exam
Similar articles
- Sine, cosine and tangent value 30°, 45° and 60°
- How easy it is to multiply by 0.
