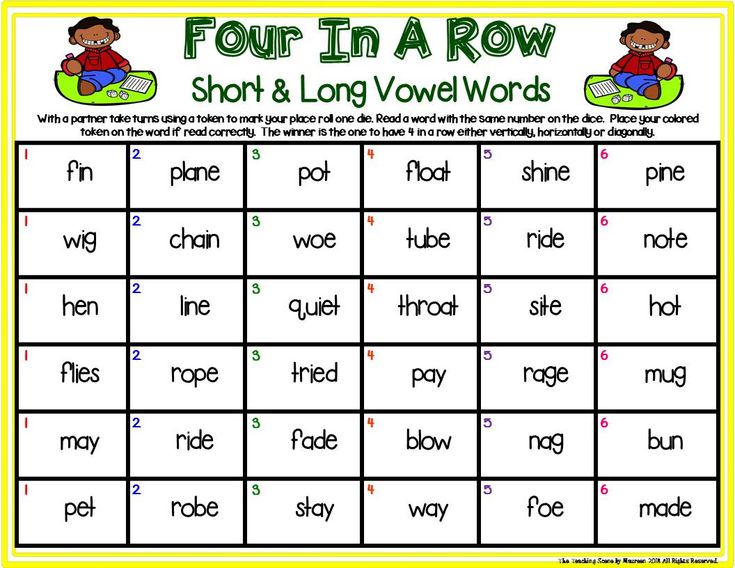
Number sense strategies
8 Strategies to Teach Number Sense to Pre-K and Elementary School Kids
Even as toddlers, the littlest of learners are learning to use their mathematical minds. The word “more” is one of the first words kids learn at the dinner table, and they are quick to learn that they want the most candy or the biggest slice of pie at dessert. Kids are constantly evaluating their world and comparing objects by quantity, size, shape, and more!
Since kids have this natural capacity to make sense of their world through mathematical concepts, it’s important to take those primitive skills to the next level by helping them make connections between their everyday observations and a more solid understanding of numbers. That’s why it’s so important to support your child’s development of number sense. But how can a parent begin teaching number sense to ensure such a concrete understanding of math concepts?
If you’re wondering how to teach number sense to your child, try the following strategies to support your little learner’s early math skills:
Storytime-advertising-container
Adsense-container
Noticing Everyday Math
Nothing is more important than engaging with your child and talking about the math you and your child experience daily. Talk about prices, budget, and quantity at the grocery store, and show your child how you use math to manage money. Practice fractions while cooking and baking, and take note of the shapes found in road signs and outdoors. Talking about the math found in everyday life sets a purpose for using and performing math processes. If kids know why math is so important in real life, they will be excited to find reasons to use it!
It’s All About the Process
Oftentimes, we get caught up with finding an answer to a math problem that we pay little attention to the process we take to solve it. Sometimes we impatiently want to find the answer quickly and move on to the next task. Instead, teach your child that the most important part of solving a problem is the way they solve it. To do this, encourage your child to look check their work and find mistakes they might have made.
Strategies for Preschool and Kindergarten Kids
Verbalizing Math Concepts
When a child describes their work and explains the process they took to solve a problem or make an observation, they are more likely to internalize what they’ve learned.
This simply means kids will remember more when they talk about it. When working with your child on a homework assignment, encourage your child to tell you how they plan to solve the problem. During completion, have your child tell you about it each step of the way. In doing so, your child will develop number sense as they internalize and understand the process they took to solve the problem.
Dot Cards
Subtilizing is the skill that refers to instantly and visually recognizing a group of objects and knowing the number just by looking. This is an important mental math skill that aids in solving problems, as well as understanding numbers. Using dot cards can help your child build this critical skill by gaining more practice recognizing groups of dots on the card.
Using Manipulatives
Learning numbers for kids can be a tough task. To make numbers make sense on paper, it’s helpful to use manipulatives that kids can use to make sense of quantity. A quick Google search for “math manipulatives” will lead you to online vendors who sell place value blocks, counters, magnet manipulatives, and more.
Manipulatives give your child a concrete way to represent numbers. In a pinch, you can even visually show your child simple addition and subtraction using Skittles or M&M’s to demonstrate the concepts for deeper understanding of math.
Check out our collection of fun math videos to satiate your kid's thirst for early number sense concepts.
Strategies for Elementary School Kids
Number Lines
There’s more than one way to solve math problems, and kids should learn different strategies to increase their number sense. For instance, using a number line can help kids make the connection between addition and subtraction or practice place value. Kids can even learn subtraction by using addition by flipping the problem around. Teaching kids multiple ways to solve problems strengthens number sense by understanding the processes they take to solve problems.
Mental Math
When kids skip count by 2’s, 5’s, or 10’s, kids are using mental math to add.
We can continue this process by asking kids to add less or more, and teaching strategies like splitting and jumping. These strategies focus on different ways to break down math problems to make difficult problems easy to solve mentally. Teaching these strategies give your child one more tool to help them understand numbers inside and out.
Make Estimations and Predictions
Place a favorite candy in a small container, and ask your child to estimate how many candies are in the bowl. Kids can solidify their number sense by making estimations and predictions based on observations. Moreover, your child will make the connection between quantity and numbers, sharpening their number sense.
Like many adults, for some kids, math can be a source of frustration and anxiety. But solving tricky math problems doesn’t need to be so difficult if only a child understands numbers and math processes. That’s why strengthening your child’s number sense makes a world of difference. When your child has a solid understanding of numbers and how they work, your little learner will have a foundation for future math success!
What All Teachers Ought To Know
Math tips and strategies for building number sense to 20 in Kindergarten and first grade: An extensive list of number sense activities and resources are included: books, materials, math manipulatives, and FREE activities!
The math tips and strategies you need for building number sense to 20 are right here.
You will have everything you need to quickly implement and bring a wealth of number sense activities, games, and centers into your classroom or home.
Building Number Sense to 20
The activities, books, resource suggestions (including a FREE one) cover a ton of number sense concepts and are perfect for Kindergarten and first grade. Plus, find valuable number sense materials and manipulative suggestions, as well as freebies you can access today! Warning: It’s LONG but filled with so much you won’t want to miss anything!
Why is Building Number Sense Important?
Children need opportunities to learn and experience numbers. Learning to count, identify numbers, and understand quantity are a few of the essential concepts. Repeated experiences build understanding and fluency with numbers. These experiences help expand knowledge and learn new ideas. A strong number sense is vital for future understanding of more complex math topics.
The activities below are ones that have been used successfully.
Use them as they are described or adapt them to your own needs. Be flexible. Have conversations about numbers and encourage questions. When there is an opportunity to order, count, match, or describe with a child, go for it! They benefit from seeing numbers in natural, fluid ways.
Make time for fun and engaging number activities daily and watch fluency develop.
Number Sense Concepts & Activities
Build Number Sense Through Counting
It is crucial to count with children every day. Repeated oral counting helps them hear what numbers sound like and to learn their order. Using math manipulatives, like counting chips, can help build a connection to verbal counting and counting objects. This one-to-one counting is an important skill that needs to be practiced often.
Activities
- Count out loud as a class starting at one and building to higher and higher numbers.
- Sit with a partner or in a circle and take turns counting by 1’s.
- As counting develops, teach number patterns and counting by 2’s, 5’s, and 10’s.
- Use a number chart to see what numbers look like visually. Point to each number as it is said.
- Encourage kids to practice one-to-one counting with small objects. Have small groups of objects set up in a center for them to count.
- Provide number cards (like those seen below) for kids to represent with counting chips.
Build Number Sense by Matching Numbers to Quantities
Provide materials for kids to count and connect with objects and numbers. This encourages children to see that numbers are more than words. Teach children that numbers have many representations, such as dots, fingers, counters, numerals, objects, ten frames, etc.
Activities
- Match two different types of objects together, such as five counting bears and a domino that shows five dots.
- Use links to create a number chain for a number.
- Work up to showing quantity with more than two types of objects (as seen in the photo).
- Have many different items available for activities, such as dice, dominoes, number magnets, bears, counting chips, cubes, and number cards.
- Match number cards from a card deck or game of Uno with dots on dominoes. Find every number combination on the dominoes.
- Complete number puzzles that have a different number representation on each piece. They help kids see that numbers can be modeled in many ways. These number puzzles to 20 are available as a FREE download further on.
- Encourage one-to-one counting with clip cards. Kids count groups of objects and clip the numeral that matches to the correct quantity.
- Ten frames are great for organizing numbers so that they can be easily counted. Matching numeral cards with ten frame representations is simple, yet effective at connecting quantity with numbers.
Build Number Sense with Number of the Day
When kids see numbers in many ways at once in a repeatedly, their number sense develops. Pick a number of the day starting at one and dissect it during your math block.
Activities
- Learn about a specific number for each day that you have been at school. Teach and dissect that number during calendar time. Represent that number on a number line, count to that number, show that number with straws or cubes, etc.
- Use a number of the day poster or anchor chart to break numbers down. Create your number of the day poster with the FREE poster templates.
- Encourage kids to participate and show their understanding on paper or mini whiteboards. Ask a question, such as “How do we show 5 with tally marks?” and allow them time to try on their own. This makes an excellent fluency building warm-up to math lessons.
- Read more tips on starting a number of the day routine in your classroom.
Build Number Sense by Ordering Numbers
Provide opportunities for kids to put numbers in order. While they put numbers or objects with numbers on them into the correct order, they are counting and building number sense.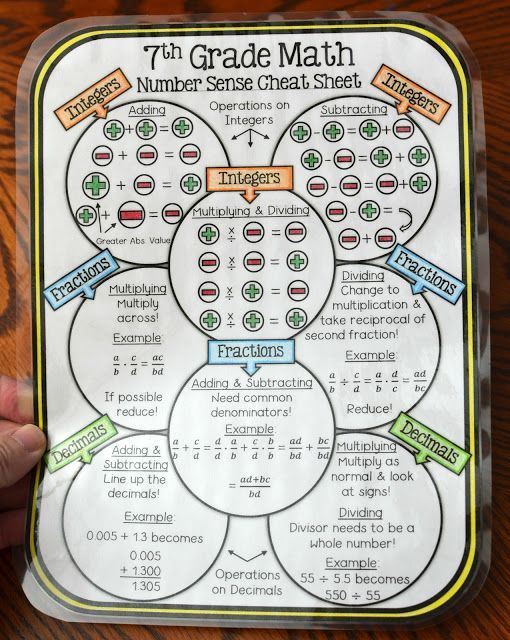
Activities
- Provide opportunities with using a number line and number chart that puts numbers in order for us.
- Give sets of numbers to order correctly by finding them on the number line.
- Cover different numbers on a number chart with sticky notes and ask kids for the missing numbers.
- Build Lego stacks by putting the pieces together in an order written on the blocks.
- Work together with a partner to order number cards from 0 to 20. Create a number caterpillar like the one seen below.
- Number puzzles are a fun way to order numbers. Put the strips in the right order to reveal a picture.
- Puzzles are simple and easy to create. Take an old puzzle and write numbers on the back of each piece.
- Grab a piece of paper and write numbers in rows. Cut out pieces randomly and trade with a partner. Put the puzzle back together again for practice.
- Complete a number order maze starting at 0.
This activity can be reused when put into a pocket protector.
Build Number Sense with Place Value Activities
Teaching kids about place value should begin with teaching them to see ten in many ways. Move on to illustrating numbers with base ten blocks.
Activities
- Practice making groups of ten things. Group straws, beans, counters, or any small objects.
- Teach counting by 10’s to count groups. Extend to teaching groups first and then singles.
- Make groups of ten to get to the 100th day.
- Show and examine a tens block and ones block. Discuss that a tens block has ten ones put together.
- Use base ten blocks to represent numbers. Do plenty of examples where kids must use and count blocks. Use a chart to help count the blocks.
- Say “Show (or draw) me 14 with place value blocks!”
- Represent the number of tens and ones on place value mats (seen below). Ask questions like “How many ones are there?” or “How many groups of ten?”.
Make sure they understand what each number within the number stands for (i.e., the 1 in 18 is a ten and not a one).
- Represent a number in different ways: expanded form, standard form, word form, numeral, etc. Worksheets like the one below, can help build this connection.
Reading and Writing Numerals
Kids are constantly surrounded by numbers in their environment. They quickly learn to recognize the individual numerals 0 to 9 through different experiences. Continue to encourage this familiarity by having numbers on the wall. Posters, number lines, and calendars are helpful tools.
Activities
- Build numbers with playdough in a math center. Even something as simple as this playdough numbers activity here.
- Print numbers from 0 to 9 daily in different ways – in booklets, on whiteboards during math lessons, etc.
- Draw numbers on paper and give students do-a-dot markers or bingo dabbers to dot numbers.
- Use a Boogie Board (seen below) or whiteboard to practice numbers over and over quickly.
- Trace numbers frequently and repeatedly to build coordination and correct form. The mini-book below encourages this, as well as locating numbers.
- Encourage the correct formation of numbers by teaching it explicitly. The posters (seen below) are helpful tools to use and post on the wall.
- Catchy number poems help students visualize and remember number formation. Use your whole body to make actions or draw in the air.
Reading and Writing Number Words
Teach kids how to read number words as they learn to read. Teach each number word one at a time and how to spell them phonetically (when applicable).
Activities
- Have number posters with both the numeral and number word on it.
- Include number words on spelling lists so that kids learn to read and spell number words.
- Use a number of the day routine to teach and focus on one word each day.
- Match numbers word cards with numeral cards (seen below).
- Play memory with a partner with number words and numeral cards. Look for pairs (twelve and 12).
- Build recognizing and speed with mental math flash cards. Flashcards to kids, and they race to call out what they see (tally, numerals, number words, etc.).
Build Number Sense by Counting On and Back
Teach the strategy of counting on and back from a number to prepare kids for addition and subtraction.
Activities
- Give students a number and a group of small objects to count on. Ask, “How many more do I have?” given 7 to start and a group of 9 counters to count on with.
- Play games with small objects and decks of cards where counting on is needed.
- Play a group counting game called ‘Around the World.’ Say a number, and each person counts on and says the next number as you go around the circle.
- Use small objects to count on or back from a number given (cubes, counters, dice, etc.).
- Put numbers in backward order.
Take the ordering activities seen above and reverse them.
Build Number Sense through Estimating
Provide lots of opportunities for kids to guess how many things they see in their day to day lives. Ask prompting questions to encourage this thinking. Make sure kids know that they are estimating and that these are just guesses. Stress that estimates do not need to be exact but that they should be thoughtful. With more practice, estimations should become closer to the actual number of objects.
Activities
- Fill clear or open containers with different sized objects for kids to guess. Keep them simple and work up in difficulty and size of objects. Smaller objects and bigger containers are usually harder.
- Create an Estimation Station,” where containers are set up with objects inside. Kids can take a close look and make estimates.
- As a whole group activity, grab a pile of objects to show quickly. Cover them and have kids make guesses.
- Play ‘Show & Hide’ with a partner. Use a cup and put some small counting bears inside. Quickly show a partner, and then hide them. They make an estimate, and then you count together to check.
Build Number Sense by Comparing Numbers
As familiarity with numbers grow, so does an ability to compare numbers with each other. Provide opportunities to compare numbers daily. Ask questions about which number is bigger, smaller, or the same.
Activities
- Use a chart or number line to compare numbers.
- Use small objects to make comparing easier. Say “Show 11 and 15 with cubes”. Ask, “Which number is smaller?”.
- Teach the symbols < > and = and what they each mean. Use the alligator strategy (The alligator likes to eat the bigger number) to remember the signs and what they mean.
- Create number towers. Kids use cubes to form towers to represent numbers. Compare two towers to see which is the tallest and, therefore, the bigger number.
The alligator eats the bigger tower. - Compare numbers with math tools and indicate the correct symbol on clip cards (seen below). As kids become fluent, they should recognize the correct symbol without support.
The activities seen in this post can be found in the following resources found on Teachers Pay Teachers.
Numbers to 5 for Kindergarten
Numbers to 10 for Kindergarten
Numbers 11-20 for Kindergarten
Mindful Math Kindergarten Curriculum
Numbers to 10 for First Grade
Numbers to 20 for First Grade
Mindful Math First Grade Curriculum
Free Number Sense Puzzles to 20
Prep this fun set of number puzzles for your classroom centers and help kids build their number sense!
Grab 20 FREE number puzzles with different representations on each piece by clicking the image below.
Number Sense Books
I Spy Numbers by Jean Marzollo
1,2,3 Peas by Keith Baker
ChickaChicka 1,2,3 by Bill Martin Jr.
Splash! by Ann Jonas (counting)
The Very Hungry Caterpillar by Eric Carle (counting)
How Do Dinosaurs Count to 10? by Jane Yolen
Number Everywhere by Elliot Kaufman
10 Black Dots by Donald Crews
How Many Bugs in a Box? by David Carter
How Many Snails? by Paul Giganti, Jr.
Ten Sly Piranhas by William Wise
None the Number by Oliver Jeffers
Zero the Hero by Joan Holub
More or Less by Stuart Murphy
Tally O’Mally by Stuart Murphy
Place Value by David Adler
What’s the Place Value by Shirley Duke
Quack and Count by Keith Baker
Betcha! by Stuart J. Murphy
Number Sense Materials
Try the Mindful Math Comprehensive Program
Read about the Mindful Math program and how it can change your math block in positive ways! This comprehensive math curriculum is available for Kindergarten, first grade, and second grade.
Learn More about Teaching Number Sense
Building Number Sense free email series
Number of the Day Activities
5 Tips for Building Math Fluency
PIN
FREE Number Sense Email Series
Sign up for the building number sense email series filled with effective strategies, must try activities, and FREE resources to build routines in your classroom.
Everything you need to help kids grow their number sense and have fun at the same time!
First Name
Personal Email Address
We use this field to detect spam bots. If you fill this in, you will be marked as a spammer.
I'd like to receive the free email course.
This form collects information I will use to send weekly emails with strategies, promotions, and resources. Unsubscribe at any time. Powered by ConvertKitLabouchere system: how to win by strategy?
Contents
- 1 How to play the Labouchere system?
- 2 Principles of Labusher Strategy
- 3 Example system
- 4 Return Labuster system (regressive system) and its example
- 5 Difference between Labusher and Martingale Strategies
- 6 Advantages
- 7 Disadvantages of the system
- 8 Examples of markets with CF from CF 2.
00 - 9 Common mistakes when playing the Labouchere strategy
The Labouchere system is a strategy in which the player determines the desired profit, breaks it into parts and then bets according to a certain principle. This principle is based on the "number series". This series is simply parts of the desired profit written in a series.
For example, the desired profit is 1000 rubles, we divide it into 5 parts: 200 rubles, 300 rubles, 200 rubles. and 300 r. Next, we write these numbers in a row: 200-300-200-300. This is the number line.
The Labouchere system is also known as the Split Martingale, the American progression and the Cancellation system. nine0003
The point of the Labouchere strategy is that you can make a profit if the percentage of your winning bets is even lower than 50 (more specifically, up to 33%).
In other words, if you win 1 out of 3 bets, the strategy remains profitable. In addition to betting, the Labouchere system is used in casinos, roulette and blackjack.
The creation of the Labouchere strategy is attributed to Henry Labouchere, who lived in the 19th century. Initially, it was used to play roulette, but later it began to be used in other areas of gambling. nine0003
This system only works with even odds markets - bets where either one selection or a second selection with 50/50 odds will play, and there is no third. It's like tossing a coin - it will either come up heads or tails. Examples of such bets: will the number “3” be in the final score, team 1 will score the 1st goal, will the total be even or odd, will the 2nd period be more productive than the 1st, etc.).
what is the Labouchere strategy
How to play the Labouchere system?
Let's explain the method of operation of the Labouchere system as clearly as possible: so, we have a number series. This series is simply the sum of the desired profit, divided into several parts. For example, the amount of our desired profit is 1,000 rubles, and we break it into 5 different parts: 100-300-100-400-100.
You can break into any number of parts - if you want to play aggressively, then break into 3-4 parts, if you want to play more carefully - break into 7-8 parts. nine0003
For the first bet, add up the extreme numbers (the very first and the very last) - and put them on CF from 2 (this is a prerequisite for the Labouchere system). That is, in our number series 100-300-100-400-100, we take the extreme numbers (100 and 100), add them up (it turns out 200) - this is the amount of your bet.
If you lose, enter the amount of this bet (100 + 100 = 200) on the far right. It turns out that our number series 100-300-100-400-100 will now look like this: 100-300-100-400-100-200. In simple words, the amount of the bet in the previous step was added to the right on the edge. nine0003
Then everything is simple: again we take the sum of the most extreme numbers (the very first number and the very last), add them up and set them. We lost - we add this amount to the right, we won - we cross out the extreme numbers.
Then again put the sum of the extreme digits.
Recall that the ultimate goal is to cross out all the numbers from the number series.
The Labouchere system in sports betting
After reading our annotated example, you will definitely have no questions left. nine0003
Principles of Labouchere's strategy
- The player's task is to cross out all the numbers from the number row.
- The entire amount in the number row - a maximum of 10% of the total bank. The total bank is the entire amount that you have allocated to your game.
- The digits of the number series are not necessarily equal. For example, you divide the amount of 1000 rubles into parts. You do not have to divide it into 10 parts of 100 rubles. or into 5 parts of 200 rubles. - you can divide into such parts as you see fit. For example, 300-200-400-100 or 500-400-100 etc. nine0006
- The optimal number of digits in the number row is 5. However, if you want to play aggressively, write only 3 digits in the number row.
If you are aiming for a long game, write 7 or more numbers on the number line. - If you have one number left in the number row, then you simply put it further.
- To protect your bank, you can enter several zeros in the numerical sequence. The more zeros in the number row, the more secure your bank is.
- Most often, the amount of the desired profit is divided into 7-8 parts. nine0006
Labouchere strategy in betting how to win
An example of a system
So, our total bank is 10,000 rubles. According to the principles of the Labouchere system, we take a maximum of 10% of this amount.
Thus, we have 1,000 rubles, which we divide, for example, into 5 parts: 100-300-100-400-100. We have a number line.
How to play further, our table with detailed explanations will show. Note that the CF of each event will be 2. Recall that the condition “CF from 2” is mandatory, otherwise the Labouchere system will not bring profit. nine0003
| Number series | How much we bet | Rate status | How much money is left after betting on odds 2 | Explanation |
| 100-300-100-400-100 | 100 + 100 = 200 | Lost | Minus 200 rubles. | Just take the extreme numbers - the left extreme and the right extreme (that is, the very first number and the very last). We stack them. We bet this amount (100+100=200). Since the bet did not work for us, we add this amount to the number row on the right. We always do this when we lose. nine0092 |
| 100-300-100-400-100-200 | 100 + 200 = 300 | Lost | Minus 500 rubles. | We have already added the loss amount on the right. Now the extreme numbers are taken again for the bet - in this case, 100 rubles. and 200 r. The bet did not play again, so again we add the amount of the lost bet to the right from the edge. |
| 100-300-100-400-100-200-300 | 100 + 300 = 400 | Won | Plus 300 rubles | nine0091 Again we put the sum of the most extreme numbers: 100 + 300 = 500 rubles.|
| 300-100-400-100-200 | 300 + 200 = 500 | Won | Plus 1300 rub. | Once again, we take the extreme numbers for the bet, add them up (300 + 200 = 500 rubles) - and put this amount. The rate has gone, so before the next rate, we again remove the extreme numbers. Recall that if the bet didn't work, we would have to record the lost amount on the right. nine0003 |
| 100-400-100 | 100 + 100 = 200 | Won | Plus 1700 rub. | The rate has gone, so we again remove the left extreme digit and the right extreme digit. We have one digit left - 400. In such cases, we simply put this one digit. |
And, already when these numbers were removed, for the bet we again take the sum of the extreme numbers. Labouchere strategy concept and examples
Reverse Labouchere system (regressive system) and its example you amounts. Therefore, the principle of the inverse Labouchere system is mirrored in relation to the classical version: if we win, then we write the amount in a number row from the far right, if we lose, then we cross out the extreme numbers.
nine0003 The required percentage of winning bets in the reverse Labouchere strategy is higher than in the classical one - it is 60.
So, our total bank this time is 15,000 rubles. We take 10% of this amount - 1,500 rubles. (we don't want to lose her anymore). We break it into 5 parts: 500-200-300-400-100.
| Number series | How much we bet | Rate status | How much money is left after betting on odds 2 | Explanation |
| 500-200-300-400-100 | 500 + 100 = 600 rubles | Lost | Minus 600 rubles. | As in the case of the classic Labouchere, we take the sum of the extreme numbers for the bet: 500 + 100 = 600 rubles. Our bet lost. Now we cross out the extreme numbers. This is the meaning of the reverse Labouchere system - since we cross out the numbers when we lose, we will not be able to lose more than a certain amount. |
| 200-300-400 | 200 + 400 = 600 | Won | Plus 600 rubles | Again we take the sum of the extreme numbers for the bet: 200 + 400 = 600 rubles. The bet has won. And now we add the amount of the bet to the right from the edge. |
| 200-300-400-600 | 200 + 600 = 800 | Lost | Minus 200 rubles. | Bet amount: 200 + 600 = 800 rubles. The bet lost. We cross out the extreme numbers - and then we put the sum of the new extreme numbers that we got after deleting. nine0003 |
| 300-400 | 300+400 = 700 | Lost | Minus 500 rubles. | Put the sum of the extreme numbers. The bet lost. The number row is over, because after the current bet we crossed out the remaining 2 numbers. |
The difference between the Labouchere and Martingale strategies
The Labouchere system is often confused with the Martingale system. The difference lies in the fact that the Martingale system is aimed at wagering with one bet, while the Labouchere system is aimed at wagering with several consecutive bets.
nine0003
Therefore, the Labouchere system is considered more reliable.
Benefits
We have counted 4 significant pluses for the Labouchere system.
- Risk management (for example, if your sequence is long, then your winnings will be higher. The reverse is also true - to reduce risks, you can make a series of 3-4 numbers).
- You don't need to win every bet to stay in the black. In simple terms, you can lose more bets than you win and still be in the black. nine0006
- The Labouchere system takes into account the individual style of the bettor, since the player himself determines how much he is going to earn and, accordingly, enter into the number series.
- Along with the Martingale, the Labouchere system is considered one of the best in betting.
Lack of the system
We have found a significant disadvantage of the Labouchere system.
- There is no guarantee that you won't have a long losing streak that could leave you with a loss.
Therefore, the system is not recommended for players with a small bank. nine0006
Examples of markets with CF from 2.00
CF from 2 is a prerequisite for the Labouchere system. Otherwise, markets with CF 2, which have only two outcomes, are called markets of equal chances. A classic example is a bet on the victory of one athlete in a match where he is opposed by an opponent of equal strength. There can be no draw. Chances should be 50/50.
Labouchere's strategy what is it and how to understand it
Below are other examples of such markets.
In football, such markets are Total Under or Over 3, Handicap (-1) or Handicap (+1), will there be a “2” in the final score, will the 1st goal be scored before the 25th minute, will goal after 80 minutes, etc. nine0003
In hockey, these markets are Total Under or Over 5, team 1 or 2 will score the 1st goal, will the 2nd period be better than the 1st, one of the teams will win by 2 or more goals, both teams will score by 30th minute, etc.
In tennis, such markets are Total even or odd, will the score be 1:1 after the first 2 sets, player 1 or 2 will win 1st point, player 1 or 2 will serve first in the game, Total of the most ineffective set is over or less than 8.5, etc.
Frequent mistakes when playing according to the Labouchere strategy
Error 1: the player has a long losing streak and continues to play.
Why is this a mistake: if suddenly 15-20 digits appear in your number series, then you simply cannot win back. In this case, it is recommended to start a new number series.
Error 2: the player bets on CF below 2.
Why this is a mistake: the basic meaning of the entire Labouchere system is to play on CF from 2. Otherwise, the system simply will not make a profit. nine0003
Error 3: The player enters too many digits in the number line.
Why this is a mistake: the more numbers, the longer the game. There are frequent cases when bettors enter 15-20 numbers, and the number line grows after each bet.
That is why the recommended maximum number of digits in a number line is 7-10.
What is the Labouchere system?
Is it allowed to use the Labouchere strategy in betting shops?
Is Labouchere's strategy suitable for beginners?
What are the main principles of the Labouchere system in sports betting?
Why is the Labouchere strategy not profitable for me?
How to play the Labouchere system?
1.3.1. Solution of matrix games in pure strategies
1.3.1. Solution of matrix games in pure strategies
The goal of the participants in any matrix game is to choose the most profitable strategies that provide player A with the maximum gain and player B with the minimum loss.
Definition. The pure strategy Ai of player A is called optimal if, when using it, the gain of player A does not decrease, no matter what strategies player B uses. The pure strategy Bj is called optimal for player B, when using which the loss of player B does not increase, no matter what strategies he uses player A.
When searching for optimal strategies, they rely on the fundamental principle of game theory - the principle of caution, according to which each player, considering his partner in the game as a very reasonable opponent, chooses his strategies, taking into account the fact that the opponent will never miss a single opportunity to use any of his mistakes in his own interests. Therefore, players must be extremely careful when choosing their own pure strategy.
Suppose player A has to make his choice. Analyzing the payoff matrix (aij)i=1,m j=1,n, for each pure strategy Ai, he first finds the minimum value of the expected payoff:
,
And then select the largest of all
And choose the corresponding pure strategy Ai. This will be the most preferable strategy of player A under the given conditions. It is called maximin, since it corresponds to the value
(1)
Definition. The number determined by this formula is called the lower net price of the game (maximin).
It shows what is the minimum payoff that player A can get by correctly applying his pure strategies for any actions of player B.
Player B, with his optimal behavior, should strive, if possible, to minimize the payoff of player A at the expense of his strategies. Therefore, for player B, the number
is found. J -th pure strategy, then player B finds his strategy for which player A gets the minimum payoff, i.e. finds the number
(2)
Definition. The number , determined by formula (2), is called the net upper cost of the game (minimax) and shows what minimum loss player B can guarantee himself due to his strategies (which, accordingly, determines the maximum gain of player A when player B chooses the right strategies). nine0003
In other words, by applying his pure strategies, player A can secure a payoff no less than , and player B, by applying his pure strategies, can prevent player A from winning more than .
Definition. If in a game with matrix A a=b, then we say that this game has a saddle point in pure strategies and a net price of the game v ==
which the equality = is achieved.
This concept has the following meaning: if one of the players adheres to the strategy corresponding to the saddle point, then the other player cannot do better than to also adhere to the strategy corresponding to the saddle point. Mathematically, this can be written in another way:
Example 2 (see Example 1 from paragraph 1.2) Analyzing the payoff matrix of the game, you can find the lower net price of the game - minus 2. Thus, for player A, the maximin strategy will be A2 - writing the numbers 1 and 2. The upper net price of the game is equal to two, and the minimax strategy for player B is B2 - writing the same numerical combination. So for reasonable reasons this game is doomed to a draw.
Example 3
Analysis of the payoff matrix H shows that <, i.e. this matrix does not have a saddle point. If player A chooses his pure maximin strategy I = 2, then player B, choosing his minimax J = 2, will lose only 20. In this case, it is profitable for player A to choose strategy i = 1, i.
e., deviate from his pure maximin strategy and win 30. Then it will be profitable for player B to choose strategy j = 1, i.e., to deviate from his pure minimax strategy and lose 10. In turn, player A must choose his 2nd strategy to win 40, and player B will respond by choosing the 2nd strategy etc.
Theorem 1. In a matrix game, the lower net value of the game does not exceed the upper net value of the game, i.e. . nine0003
Proof. A-priory ; . Combining these ratios, we get . From here or . This inequality is valid for any combinations of i and j. It will also be true for those i and j for which the maximum and minimum values and are realized. Q.E.D.
Investigation in matrix games begins with finding its saddle point in pure strategies. If a matrix game has a saddle point in pure strategies, then finding this saddle point ends the study of the game. If the game does not have a saddle point in pure strategies, then one can find the lower and upper pure prices of this game, which indicate that player A should not hope to win more than the upper price of the game, and can be sure of receiving a payoff no less than the lower one.
