Numbers recognition activities
10 Number Recognition Games
Number recognition is a key skill to learn during the early years, and there are many ways in which you can encourage this in your early years setting. We’ve already explored activities to support the development of numeracy skills in general; in this article we’ll concentrate specifically on helping children to learn their numbers.
When planning number recognition activities, there are a few points to keep in mind:
- Make sure you have plenty of relevant resources available (e.g. number beads, blocks, stickers, cutters, stamps etc.), as well as visual cues (e.g. posters on the walls).
- As well as using numerals it’s also helpful to look at other representations of numbers with the children, including words and tallies.
- Try to make number activities fun in order to nurture a positive approach to maths.
1. Number bubble game
Draw lots of chalk circles on the ground outside, with a number inside each (1 to 5 or 1 to 10, depending on how much space you have), distributing them evenly so that you end up with several 1s in circles, several 2s in circles, and so on (make sure you have enough for each child playing the game). Call out a number and each child has to find a circle (bubble) with that number and stand in it. Make it more fun by blowing bubbles over the children in between each round.
Take a small group of children out for a walk around the neighbourhood – or perhaps combine it with a visit to the local park – hunting for numbers along the way. There should be plenty of opportunities for number spotting, for example on front doors, gates, buses, cars, posters etc. Get the children to call them out when they see them.
A number hunt is a great way for children to practice number recognition outside your setting
3. Giant dot-to-dotMake your own giant dot-to-dot in the playground, by chalking numbers on the ground that the children have to connect in the right order to make a shape or picture. For younger children stick to simple shapes using fewer numbers; for older children you can make it a bit more difficult.
Sign Up to Receive this 20-Part Activity Email Series
4.
Conker countGo to the park and collect some conkers. Back at the nursery, draw the numbers 1 to 10 on the ground in a row with chalk, using both numerals and words, and get the children to line up the right number of conkers underneath each one. (Obviously outside conker season there are plenty of other objects you could use for this activity, eg petals, leaves or items from inside.)
5. Dice tallyTake a sheet of card and make a grid of six squares, labelling them 1 to 6 using both numerals and words. Roll a die and keep a tally in the squares of how many times each number comes up. Children could do this individually, each with their own separate grids, or in pairs or small groups using the same grid but their own dice. You could turn it into more of a game by adding a competitive element.
Recognising and tallying the numbers rolled on dice is another good skill to develop
6. Musical number tiles
This is a musical variation of the bubble game.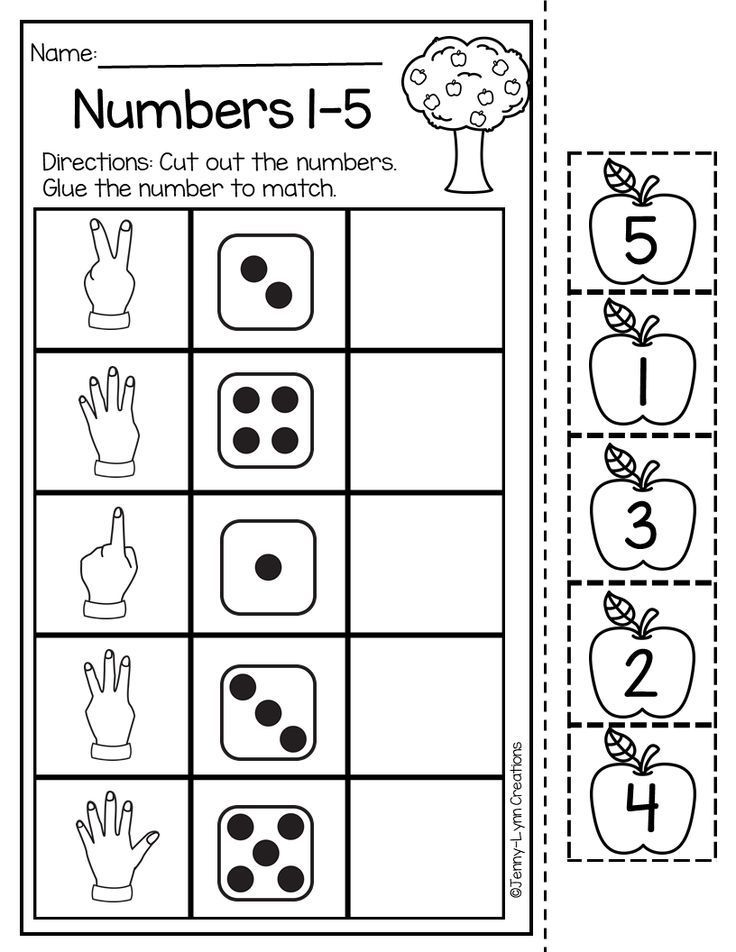
Lay out some foam number tiles on the floor, making sure you have plenty for all of the children playing (if you don’t have foam tiles, make your own using some card but tape them down so that they don’t slip). Play some music and get the children to dance around; when the music stops, call out a number and they have to jump onto a corresponding tile.
Using some number shape cutters, make some sets of number biscuits with the children and then use squeezy icing to stick the right number of decorations onto each biscuit (e.g. eight raisins on the number 8, three raspberries on the number 3 etc).
Help the children make biscuits with different numbers of decorations, counting them out as you put them on
8. Beanbag toss
Here are a couple of ideas for throwing games to help with number recognition. One is to get a set of buckets and label them 1 to 5 (or 1 to 10), then the children have to try and throw the right number of beanbags into each; another is to use a target mat and the children have to try and land the right number of beanbags in each numbered segment.
For this activity you’ll need ten paper plates, some coloured pens and some coloured beads. Write the numbers 1 to 10 on the plates, using a different colour for each number. Get the children to put the right number of beads onto each plate; this works particularly well using coloured beads that correspond with the colours used to write the numbers, as it gives the children a strong visual cue.
10. Number craftsThere are lots of ways in which you can incorporate number recognition into craft activities. One idea is to draw some outlines of ladybirds on a piece of paper, then number them and get the children to add the right number of spots to each. A couple of variations on this include drawing birds and sticking on tail feathers, or drawing monsters and sticking on googly eyes.
One option for a number craft is sticking the correct amount of spots on a ladybird
Related Itemscognitive developmentnumbersnumeracy
23 SIMPLE Number Recognition Activities
Let’s talk about some SIMPLE ways you can teach your children about the numbers.
I always appreciate it when things are easy to set up, teach, and implement to my kids! I am a working mom, so I try to plan fun and simple activities, so my kids can learn!
Number recognition and counting in numerical order are essential skills that all of our kids need to know! It’s one of the first skills preschool work on to get them ready for kindergarten!
So, let’s dive into my 23 SIMPLE Number Recognition Activities For Kids to help you learn how to teach numbers to your kids!
Activity #1: DIY Number Cards
Do you order from Amazon a lot?
I know I do! Don’t recycle those boxes just yet! You can use them for some activities.
How to do this activity:
1. Materials you need- medium/large-sized cardboard box, sharpie, clothespins, and stickers/mini erasers.
2. Cut the cardboard box into a square shape, big enough to write a few numbers on it, and place the stickers or mini-erasers.
3. On the bottom part of the square, write 3 different numbers in sharpie and give your child a clothespin!
4. Put a specific amount of stickers or mini erasers on the large part of the square and have your child place the clothespin the correct amount number of corresponding items.
5. Got an older child? Instead of writing numbers, write tally marks or dots, so they have to use higher-level thinking skills to answer the questions.
Activity #2: Swat the Number
Wait, your kids can actually hit something, and it’s okay?
Yes! They will be so excited. Swat the number is an activity where your kids can use fly swatters to smack the correct number.
How to do this activity:
1. Materials you need- fly swatters and numbers 0-20.
View/ Check Amazon's Price
2. Set out the numbers on the floor and ask your kids to find a specific number and swat it with the fly swatter!
3.
Another way to play is to have the kids swat a number and tell you what number they hit.
Simple as that!
Activity #3: Stamping Numbers
You can use letter stamps in several different ways. I have used them on paper, and I also have used it in Play-Doh.
How to do this activity:
1. Materials you need- art tray, Melissa and Doug alphabet+number stamps, Play-Doh and paper
View/Check Amazon's Price
2. Flatten out Play-Doh on a tray and stamp numbers on the Doh! You can put numbers in number order, practice teen numbers, and even practice some math facts since there are math symbols included in this pack.
3. Another way to talk about number recognition is to stamp numbers on the play-doh and ask your child to find specific numbers!
Activity #4: 1:1 Correspondence
The best thing about 1:1 correspondence is that you can use any object that you have lying around the house to do activity!
I do like to have a specific theme, but you don’t have to do that.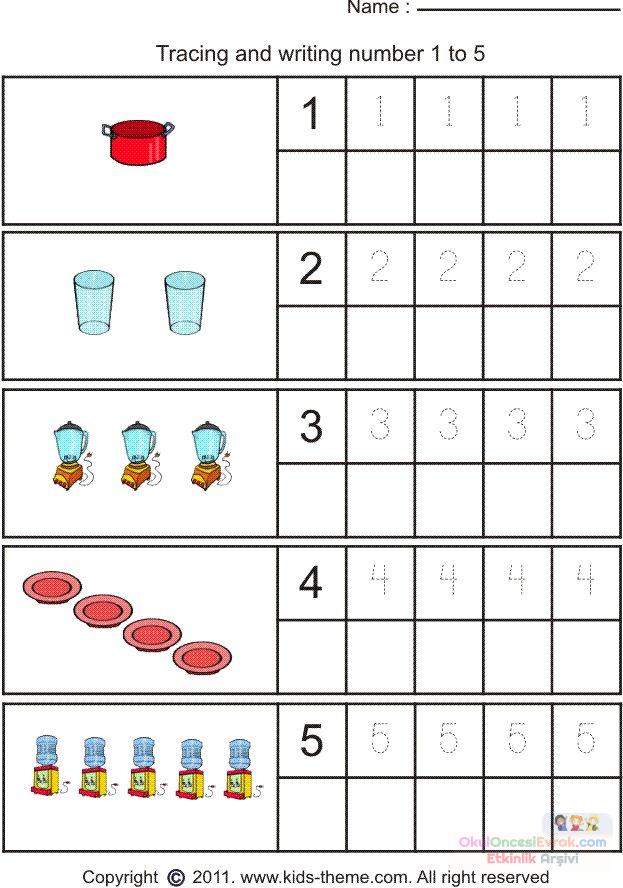
All 1:1 correspondence means is that you have a number out for your child to see, and they have to match the amount of objects to the number.
How to do this activity:
1. Materials you need- an object that you want to use as the manipulative (eggs, cars, bows, pom-poms, etc.), a marker, stamper, or moveable numbers like magnetic numbers.
2. Place or write the number down on a sheet of paper or the floor, depending on what you are using!
3. Have your child count out for each number how many objects they need to place next to each number, as you see above.
4. For younger kids, start with numbers 1-5. For older kids, you can do as many as you’d like!
Activity #5: Number Search
Bringing in some number play while doing a sensory activity? OH YA! Your kids will love it.
Many sensory bin fillers can be used for number searches, but this is the one that worked well for us!
In this bin, are colored chic peas! I made them green and red to go along with an apple tree theme from the book Chicka Chicka 1, 2, 3.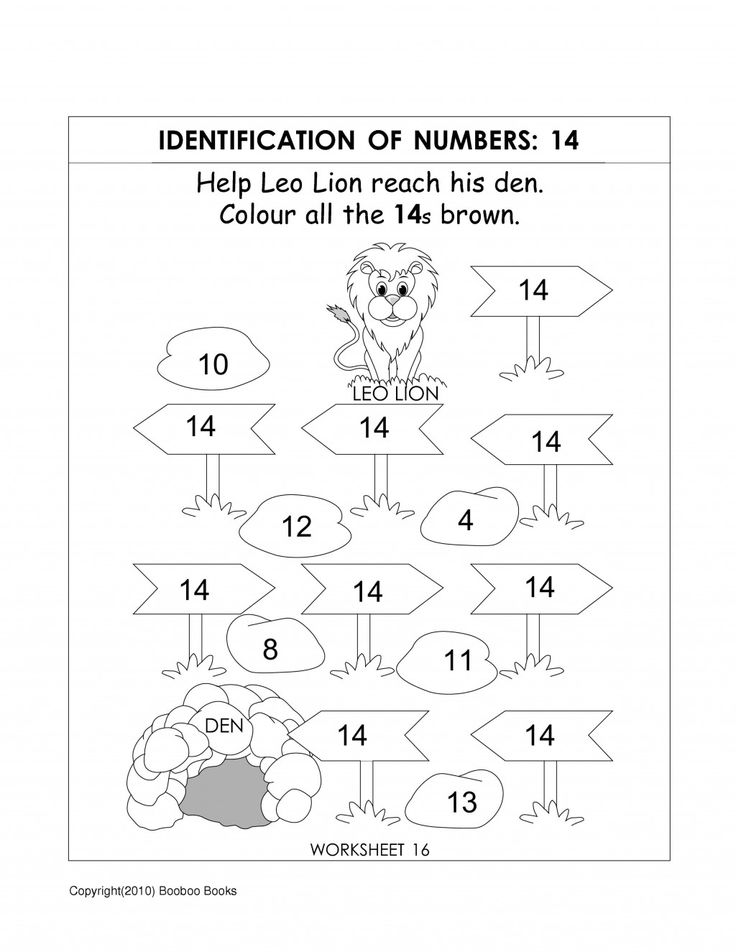
How to do this activity:
1. Materials you need- tray, 2 bags of chic peas, liquid watercolors, FREE APPLE NUMBERS WORKSHEET, and numbers.
View/Check Amazon's Price
2. In a ziplock bag, dump a bag of chickpeas and squirt a bunch of liquid watercolor into the bag.
3. Zip it up and shake, shake, shake! Make sure to cover as much of the chickpeas in the color as you can.
4. Repeat this step if you want to do another color in a separate bag.
5. Line a baking sheet with parchment paper and dump the colored peas out to dry. Let them dry for at least a half-hour before play. The liquid watercolors dry pretty quickly!
6. Once dry, dump them into a medium-sized container and hide numbers throughout the chic peas.
7. Download my Apple Numbers for the kids to match up numbers when they find them!
Don’t have the book? You don’t have to go out and buy it, have your little one listen to it online!
RELATED: THE BEST 22 SENSORY BIN IDEAS FOR KIDS
Activity #6: Geoboard Number Building
Does anyone remember using these boards when you were younger? I remember teachers busting these out every now and then for us to use!
You can create numbers, letters, make sight words with multiple boards, or just have fun and create whatever design you want!
Plus, this is a fine motor activity, so it works on increasing those little muscles to be able to do critical everyday tasks like zipping up their coats or buttoning their shirts.
How to do this activity:
1. Materials you need- geoboards (they come with the rubber bands)
View/ Check Amazon's Price
2.
Encourage your child to try to make specific numbers; some will be easier than others due to the curves. However, you can still create those numbers; they just will look more box-like.
3. If your child can’t do it on their own, you can create the number and work on number recognition skills by asking what number it is.
4. For older kids, you can even create addition and subtraction problems using these boards!
Activity #7: Number Line
Kids LOVE sticky notes. I know, right? Sometimes, it’s the simplest things.
While I was setting this activity up, my oldest was making letters to all of us on sticky notes and hiding them! I’m telling you, they love these things.
How to do this activity:
1. Materials you need- post-it and sharpie
View/Check Amazon's Price
2. On the post-its, write as many numbers as you want to practice with your kids.
My recommendation would be to first start by writing numbers 1-10. For older kids, you can write 1-20.
3. Place the post-it’s on the wall in a mixed-up order. Have your child place them in numerical order on a different wall, so they don’t get confused by all the different sticky notes!
4. For older children, make this more challenging by placing some numbers on the wall and ask them to find the missing numbers and fill them in!
Activity #8: Egg Carton Counting
It’s actually near Easter time while I’m writing this, but this activity can be done at any time!
My kids are obsessed with plastic eggs. They love putting things inside them, even when it’s not Easter time, especially if candy is involved.
How to do this activity:
1. Materials you need- egg carton, plastic eggs and candy (jelly beans/M&M’s)
2. Write the numbers on the plastic egg with a sharpie- if you use a dry erase marker, it will come off when your child touches it!
3.
You can write the numbers on the bottom of the carton as well so they can match it up or you don’t have to! Have your child match up the number egg to the place it should go in the egg carton in numerical order.
4. To extend this activity, you can have your child place the correct amount of candies to match the number in the egg! They will enjoy this part; sometimes we need to bring in a little something extra, don’t we?
Activity #9: Tactile Sticks
The possibilities are endless here! I love doing holiday-themed things, and my favorite one that I have done recently is my Halloween themed tactile sticks.
These sticks can be done with googly eyes, small pom poms, glitter glue dots, or even small hair ties!
View/ Check Amazons Price
How to do this activity:
1. Materials you need- popsicle sticks, glue, and whatever object of your choice listed above!
2.
On each popsicle stick, write a number 1-10.
3. Have your little one say what number is on the stick, then count out how many pieces of supplies that they need to glue on each stick. This works on number recognition and numerical counting.
4. Remember, a little dot does a lot 🙂 So, a small amount of glue for each object is perfect!
Activity #10: Bath Number Puzzle
Bath crayons are the BEST!
It’s a way for the kids to draw on the walls of your house and not ruin anything! If I could insert an emoji here, the double high five’s would be right here!
For most kids, bath time is a lot of fun, but sometimes kids don’t like it. This could be a way to help excite your kids at bath time while learning.
How to do this activity:
1. Materials you need- bath crayons and bath foam numbers
View/Check Amazons Price
2.
With a bath crayon, trace the numbers you want to teach/ review on the bath wall.
3. Have your child say the number if they can before they match up the foam number or just attempt to match the correct number with the shape that’s on the wall!
4. With an older child, have them trace the numbers to get some handwriting practice! Or, you can even write a few numbers on the wall and have them find the missing numbers to challenge them.
Activity #11: LEGO Block Count
Your kids will be so excited to count when LEGO blocks are involved! The best thing about this activity is that it can be toddlers and for early elementary-aged students!
How to do this activity:
1. Materials you need- LEGO blocks and a dry erase marker
View/Check Amazons Price
2. With toddlers, I would write numbers 1-10 on the blocks and have them stack them in order.
For preschoolers, you can do 1-20.
3. To challenge early elementary students, you can practice skip counting by 2’s, 5’s, or 10’s!
Activity #12: Pipe Cleaner Count
I started doing some fine motor activities with my son, he’s 2, and he just fell in LOVE with doing these sorts of activities.
I swear this kid is going to be some sort of engineer or something. Your kids will enjoy this learning challenge.
How to do this activity:
1. Materials you need- pipe cleaners, beads, paper, marker, and a flat surface like an art tray!
(Picture of tray)
2. On small pieces of paper, write how many numbers that you can fit on your flat surface that you want your child to practice.
3. Tape down a pipe cleaner underneath each number and have a bowl of beads ready for your child.
(Choking hazard: make sure your child is old enough to do this activity so that they won’t put the beads into their mouth).
4. Have your child string the amount of beads associated with the number above the pipe cleaner. Little ones will need help counting out the correct number, but they can try to string the beads on their own!
5. Have the older kids try to do this on their own without assistance! You can even have them make a specific pattern with colors to make this a bit more challenging for them.
Activity #13: Do-A-Dot Number Painting
Do-A-Dots are one of our favorite supplies around here!
If you haven’t used them, you are missing out! It’s a way to paint with your kids that they won’t get messy.
GRAB YOU FREE Do-A-Dot Numbers 1-10 WORKSHEET HERE!
How to do this activity:
1. Materials you need- My Do-A-Dot Numbers 1-10 FREE Worksheet and Do-A-Dot painters
View/Check Amazons Price
2.
Download and print my number printable and ask your child to name the specific number that you are focusing on. If they don’t know it, that’s okay! Tell them the number and have them try to use the painters to fill in the dot.
3. The numbers around the dot are there to help your child differentiate between numbers. They should focus on painting the number in the circles that go along with the big number on the page.
Activity #14: Pom Pom Number Matching
It’s always nice to have an activity that you know you can pull off using what you have at home!
It always makes things more complicated if you have to order something or run out to the store. I always tend to put those activities on the back burner, which sometimes means I even forget about them.
This is a fine motor activity that builds up small muscles in your children’s hands so they can do daily activities like write their name, tie their shoes, and zip their jackets!
How to do this activity:
1.
Materials you need- cupcake tin, 12 cupcake holders, a marker, pom-poms, and kid-friendly tweezers.
View/ Check Amazon's Price
2. On the bottom of 12 cupcake liners, write the numbers 1-12 and place them inside the circles in numerical order.
3. In a bowl, place the pom-poms in and show your child how to use the kid-friendly tweezers. Have them pick up a pom-pom and place it in the first liner. Explain that depending on what number is on the bottom of the liner, that’s how many they should put in.
Activity #15: Sensory Bag Game
If you have read some of my other content, you know how much I enjoy a good sensory activity.
This sensory game is so much fun, plus it’s a great way to work on number recognition!
How to do this activity:
1. Materials you need- 2 bottles of hair gel, a large ziplock bag, sharpie, food coloring, and plastic coin.
2. On the bag, write whatever numbers you want to practice with your kids (1-10, 11-20, 100’s, 1,000’s).
3. In the ziplock bag, squirt both hair gels packs inside, drop several drops of food coloring in, place the coin in, and zip the bag shut.
4. Massage the bag, so the food coloring and hair gel get all over the bag!
5. Ask your child to find a specific number. They should move to the coin through the bag over to that number! Repeat this until you have gone through all the numbers!
Activity #16: Giant Number Matching Game
I did this game with the alphabet, and it was such a hit I decided to try it with numbers!
This is such an easy set-up, and I always have paper plates on hand, which makes things easier since it’s already at home!
How to do this activity:
1. Materials you need- paper plates and marker
2.
On paper plates, write which numbers you want to work on with your kids. Make sure you write 2 of the same number since it’s a match game.
3. Spread them out all around the ground, making sure that the pairs aren’t right next to each other!
4. Have your kids flip one plate over, look at the number, they should say it then flip another plate over to see the number. If it’s a match, they can leave both plates flipped over. If it wasn’t a match, they need to turn it back to its original side and try again.
5. Play until all the plates are flipped over, and all the matches are found!
Activity #17: Tray Number Writing
Did someone say sprinkles!?
Any child will be engaged in an activity where sprinkles are involved. We used confetti sprinkles, which is great because they are a little larger.
This is an excellent pre-writing activity! Especially if your little one struggles with handwriting with a pencil, this is a great alternative to get some practice in to give them confidence!
How to do this activity:
1.
Materials you need- MY FREE TRACIBLE NUMBER CARDS DOWNLOAD HERE, a flat tray, sprinkles, and a paintbrush
2. On a tray, dump out the container of sprinkles. Then, place the tracing card of your choice on the front of the tray.
3. Before your child attempts to write the number with their paintbrush, they can use their finger to trace the number, so they get the hang of the shape of the number.
4. Then they can use the paintbrush to copy the number shape on the sprinkles!
RELATED: 15 FUN HANDWRITING ACTIVITIES FOR PRESCHOOLERS
Activity #18: Ice Cream Counting Sensory Bin
This is one of my FAVORITE sensory bins that I have ever done.
The ice cream bin can be used as an educational bin because you can ask your child to put a specific amount of cotton balls+ sprinkles into a bowl.
How to do this activity:
1.
Materials you need- medium-sized container, cotton balls, small colored pom-poms, ice cream bowls/plastic cones, and scoops! We also have ice cream set from Melissa and Doug, that’s where I got the little menu and the 4 scoops that you see in front of the bin.
View/Check Price
2. In the medium-sized bin, cover the entire tray in cotton balls! Add in some of the small pom poms to be the sprinkles for the ice cream! Add in all of the other little things like the bowls and scoops.
3. Help your child learn with this bin by asking them to put a certain number of cotton balls and sprinkles into the bowls, work on addition skills by getting two bowls out to add small amounts together and work on color recognition by asking for specific colors of sprinkles!
4. Have an older child at home? Challenge them by doing my FREE ICE CREAM ADDITION WORKSHEET!
Kids can work on adding small numbers together to see how many scoops of ice cream need to end up on the last cone! You can even make the worksheet come to life by adding in colored pom-poms to the bin instead of cotton balls!
Activity #19: Puzzle Work
The reason why my children were able to learn their numbers was because of our daily practice with the Melissa and Doug number puzzle.
Seriously, all it takes is 5 minutes each day, and you will see considerable improvements in their number recognition.
View/ Check Amazon's Price
Being able to manipulate the number and have a place for it to go helps your child remember the number better than doing other activities, in my opinion.
How to do this activity:
1. Materials you need- Number puzzle (I recommend the one above because it has numbers 1-20, it can be used for longer and is only a few more bucks than 0-10).
2. Focus on one or two numbers a day; once they have mastered those, you can move on to another few.
3. I would recommend starting with numbers 1-10 and moving onto the teens when they comprehend the first 10.
4. Every day for at least 5 minutes, practice the dew numbers that you are focusing on. Ask them several times to point to the numbers you are saying and place it in the spot where it should go.
5. Tip: If your child gets distracted with all the other pieces, hide them so they aren’t a distraction, and they can focus on the few they need to learn.
RELATED: HOW TO TEACH YOU TODDLER NUMBERS (9 SIMPLE STRATEGIES)
Activity #20: Cupcake Play-Doh Counting
Play-Doh cupcakes?! This is sure to excite your kiddos in wanting to play with numbers.
How to do this activity:
1. Materials you need- Play-Doh, silicone cupcake holders, magnetic/ play numbers, + candles
View/Check Amazon's Price
2. Have your child roll up as many Play-Doh balls as you have silicone holders out for. I used 6 just because that’s what fit on my tray, but feel free to use more or less!
3. You can also work on color matching by using the corresponding color Doh with the holders!
4.
In numerical order, place numbers by the silicone holders, and your little one can start placing the corresponding number of candles in the Play-Doh.
Activity #21: Egg Matching Activity
Yes, there are several plastic egg activities on this list, they can be used for so many educational activities, it’s fantastic!
This is a subitizing activity, so if you have older ones, this is GREAT for them.
FACT: Everything always looks more enticing when it’s placed in a sensory bin :).
How to do this activity:
1. Materials you need- medium-sized container, Easter grass, and plastic eggs
View/Check Amazon's Price
2. In the container, put the Easter grass inside.
3. On the plastic Easter eggs, write a number on the top half and on the bottom half write either tally marks or dots that correspond to the number you wrote on the top half.
4. I would suggest doing numbers that your child knows since this is a subitizing activity and is a bit more challenging.
5. Break the eggs apart and hide them throughout the Easter grass in the bin.
6. Have your child try to connect the right egg pieces together! Help them if they are having a hard time with this by showing them how to count using tally marks or dots!
Activity #22: Dot Sticker Numbers
Dot stickers are one of my MUST-HAVE supplies to have on hand at home.
Why? Because they are so versatile! I have an endless amount of activity that they can be used for, which is nice.
Anyone’s mind go to garage sale stickers when they see these? My family always had garage sales growing up, and that’s all I can think of when we use these stickers!
How to do this activity:
1. Materials you need- butcher paper, dot stickers, painter’s tape, and a marker
View/ Check Amazons Price
2.
On a piece of butcher paper, write the numbers that you want, so it covers most of the paper.
3. Have your children peel off the stickers if they can and place them on the lines of the letters. Try to encourage them to put the stickers on the lines of the letter right next to each other.
4. Make sure to talk about each number as you get to it, and when the stickers are all placed on, you can repeat the numbers.
5. Challenge older children by having them count how many stickers that it took for them to cover up each number!
This is an excellent fine motor activity as well!
RELATED: My 10 FAVORITE Learning Supplies For Kid’s Activities
Activity #23: Number Hopscotch
Active learning is my favorite kind of learning!
I am a physical education teacher, and it just makes me so happy to see my kids working on some gross motor or locomotor activities while learning.
This activity can be used as a hopscotch game or a throwing game! Win, win, right?
How to do this activity:
1. Materials you need- painter’s tape and bean bags
View/ Check Amazons Price
2. With painter’s tape, make a hopscotch set-up as you see above. I wrote the numbers 1-10 in each of the squares, but you can also practice even numbers, odd numbers, or larger numbers!
3. You can have your kids play with the hopscotch course, and they can say the numbers that they land on when they get to them!
4. Make this into a learning game by getting out some beanbags and work on some throwing! Have your kids try to throw a beanbag and have it land on one of the numbers. Have them say the number it lands on!
5. Got older ones? Work on addition by having them throw two beanbags and add the numbers that they landed on together!
Final Thoughts and Conclusions
Teaching your kids at home can be simple with these 23 number activities! Making learning fun makes it more memorable for your kids, which will help them understand the content better.
These activities are great for toddlers, preschoolers, and can even be modified to challenge early elementary students! Make sure to read through my post thoroughly to see how you can challenge each age level!
I’d love to hear about some activities that you do at home or school with your kids! Please leave a comment below to share them with our community!
Happy Learning!
Development of numerical literacy of children in preschool institutions
Arthur J. Baroody, PhD
College of Education, University of Illinois at Urbana-Champaign, USA
(English). Translation: June 2015
Introduction
There has been a long discussion about how best to help children learn how to perform addition and subtraction with elementary numbers (for example, 3+4=7 and 9+5=14; 7–3=4 and 14– 9=5) (see Baroody & Dowker 1 , especially chapters 2, 3, 6 and 7).
However, scientists agree that children need to achieve a certain level of fluency in elementary calculations 2 . Such fluency implies the efficient (fast and accurate) calculation of the sum and difference in examples, as well as the correct and flexible application of this knowledge. Over the past 40 years, it has become obvious that everyday (informal) mathematical knowledge of children is the basis for learning (formal) mathematics at school 3,4,5 . For example, studies show that developing children's sense of numbers contributes to fact fluency 6,7,8,9 . The purpose of this article is to summarize the data on how the development of ordinary number sense before the first grade of school provides the basis for the formal skill of fluency in elementary calculus, which is key in the primary grades.
Key Questions
- When should parents and preschool teachers begin to (a) help develop a child's sense of numbers and (b) directly develop children's fluency in elementary calculus?
- What age prerequisites should children have initially in order to quickly and effectively achieve fluency in elementary calculations?
- What role does language play in the development of this basic knowledge?
- How can parents and preschool teachers best encourage the development of a sense of number and fluency in elementary calculus?
Recent Research Results
Question 1.
Helping children develop their sense of numbers - the basis of fluency in elementary calculations - can and should begin as early as preschool age. Recent research shows that children begin to develop a sense of number very early. In fact, toddlers as young as 18 months and almost all children as young as two years of age already have the initial inclinations required for fluency in elementary calculus (see review by Baroody, Lai & Mix 3 ).
The effectiveness of efforts aimed at increasing fluency in elementary calculations depends on whether the child is ready for learning in terms of age, and on the pace of learning offered to him. As recent studies show, significant individual differences in number sense appear as early as 2-3 years of age and often increase with age 3.10 , as a result of which there are no strict prescriptions for when to begin the systematic development of fluency in calculations. Of course, for many children, due to the peculiarities of their development, this teaching of even the simplest calculations (n + 0 and n + 1) should begin no earlier than the last year of kindergarten or the first grade of school 11 .
For children who are predicted to have a high probability of academic failure, problems with elementary numbers most likely do not make sense to offer up to the first or second grade of school 12 . Questions 2 and 3 13 ). More specifically, language provides the foundation for two basic components of early childhood number sense, namely the notion of the cardinal number of the set (the total number of elements in the set) and the capacity for verbal number recognition, VNR, sometimes called "verbal subitization", which is noted at the top of Figure 1 . TCG means accurately and quickly determining the number of elements in small sets and naming them with the appropriate numeral. The use of the words "one", "two", "three" in combination with the demonstration of relevant and irrelevant examples can help children 2-3 years old develop an accurate and reliable "intuitive understanding" of numbers one, two, three - understanding when something is one, something two, something three.
- By seeing pictures of ●●, ∆∆, and o o (relevant examples of pairs) and hearing them denoted by the numeral "two", children can understand that the appearance of the elements of a set is not important (shape and color do not affect the quantity). Also, as a result, they may have the designation "two" for the intuitive idea of the multiplicity of (there are more than one).
- By seeing pictures of ●, ●●●, ∆, ∆∆∆, , and (irrelevant examples of pairs) indicated by the words “not two” or another numeral, children can determine the boundaries of the concept two .
A key recommendation for such tasks is that the basic understanding of the cardinal number of a set is not innate and does not develop automatically during ontogeny (cf. Dehaene 15 ) 14.16 . Parents and preschool educators play an important role in this process as they provide the experience and feedback needed to form the concept of number. Therefore, they should use everyday situations to indicate small sets and encourage children to do the same (for example, “How many feet do you have?” - “So you need two shoes, not one” or “You can take one cookie, but not two ").
Some children start going to kindergarten before they have learned to distinguish all the "intuitive" numbers. Such children are at serious risk of being among the underachievers in school and need intensive remedial classes. When diagnosing the abilities of kindergarten students, it should be checked whether children can quickly distinguish sets of one, two and three items and distinguish them from somewhat larger sets of four and five items.
As shown in Figure 1 , the interrelated development of the cardinal concepts of intuitive numbers and the ability to verbally recognize numbers can provide the foundation for a wide range of numerical, counting, and arithmetic concepts and skills. These skills can provide the basis for meaningful verbal counting. Recognizing "intuitive" numbers can help children see visually that the group labeled "two" includes more items than the group labeled "one" and that the group "three" includes more items than the group "two". This basic understanding of ordinal numbers will in turn help children understand that the order of numbers is important when counting ( the principle of ownership of the number series ), and that the sequence of numbers (“one, two, three ...”) reflects the increase in the number of elements in the set. Once the child masters the sequence of counting words, he develops the ability to start counting from any number and (correctly) call the next number in the sequence ( skill of determining the next number ) without starting again from one.
The ability to automatically name the next number in a counting sequence can be the basis for realizing that adding one to any number creates a larger number and, further, for mastering this operation when rearranging the terms in the examples n + 1 / 1 + n. When one is added to a number, the sum is the next number in the counting sequence (for example, the sum for 7+1 is the next number after seven, or eight). This reasoning strategy will help children calculate sums in similar combinations if they know the counting sequence, including even multi-digit numbers such as 28+1, 128+1 or 1000128+1.
Over time, this reasoning strategy becomes automatic; can be effectively applied without thought (becomes a component of the playback/retrieval system). In other words, it becomes the basis for fluency in solving n+1 / 1+n combinations.
TCG and an understanding of the order of counting that it includes can form the basis for a meaningful counting of objects 17 . Children who can distinguish between "one", "two", and "three" learn to count objects more easily with the help of adults than children who cannot distinguish between these numbers. They also have a better understanding of the purpose of counting (one way to determine the total number of items) and the reasons for certain actions in the counting process (for example, someone repeats the last word in a count to emphasize that this is the total number of items). Meaningful counting of objects is needed to develop counting strategies (using objects or numbers) in order to determine sums and differences. Once these strategies are established, attention shifts to the exploration of orders and relationships; these mathematical patterns, in turn, serve as the basis for reasoning strategies (that is, how the child will solve an unfamiliar example using the examples and relationships known to him).
Once these reasoning strategies become automatic, they can serve as one strategy for efficiently retrieving responses from memory.
TCG allows the child to see the combination "one+one" as "two", "one+one+one" as "three" and vice versa (for example, "three" as "one+one+one"). Thus, the child constructs an understanding of combination and decomposition (the whole can be made up of several parts or broken into parts in different ways). If a child constantly sees before him examples of the combination and decomposition of "two" and "three", this will lead to the development of fluency in calculations of elementary sums and differences ("one plus one equals two", "two plus one equals three" and "two minus one equals one"). Decomposing "four" and "five" into parts with feedback (for example, a child calls a group of four objects "two plus two", and another person confirms: "Yes, two plus two is four") can lead to fluency in elementary calculations. sums up to five and using the "next number rule" in n+1/1+n combinations (as discussed earlier).
The concept of cardinality, CCG, and the concepts of addition and decomposition into components provide the basis for the formation of the concepts of addition and subtraction. For example, adding one object to a group of two objects, the child clearly sees that the original group is transformed into a larger group and already consists of three objects. Such competencies, in turn, serve as the basis for the formation of a concrete-abstract understanding of the following arithmetic concepts 18 :
- The concept of subtraction to zero (subtractive negation). For example, children realize that if two blocks are removed from two available blocks, then nothing remains. This realization can develop into a generalization that if you subtract it from any number, then nothing remains.
- The concept of quantity immutability (additive and subtractive identity). For example, when children understand that if two dice are subtracted from zero, then two dice remain, they can develop a generalization that subtracting zero from any number will leave that number unchanged.
Both concepts serve as the basis for the development of fluency in elementary calculations of examples of type n – n = 0 and type n – 0 = n.
A poorly developed sense of numbers can interfere with the achievement of fluency in elementary calculations and the achievement of success in mathematics. For example, Mazzocco & Thompson 19 found that the performance of preschoolers on four types of items from the Test of Early Mathematics Ability – Second Edition; learning mathematics in the second and third grades. These tasks include the following: meaningful object counting (with the knowledge that the last number is the number of objects), the concept of cardinality, comparing single-digit numbers (for example, “Which is greater - four or five?”), addition of single-digit numbers in the mind and reading the corresponding numbers. It should be noted that the ability to verbally recognize "intuitive" numbers is one of the foundations for the first three skills mentioned above and a significant factor in mastering the fourth.
Question 4. In order to stimulate the formation of a sense of number in general and fluency in elementary calculations in particular, it is necessary to create opportunities for children to explore patterns and relationships. For example, a child who has learned in a meaningful way "pairs / doublings" "5 + 5 = 10", "6 + 6 = 12", etc. (for example, the child understands that all such sums are even, or divisible by two), can use this knowledge to calculate unknown sums of the “pair+1” type: for example, 5+6 (i.e. 5+(5+ 1) or (5+5)+1) or 7+6.
In order to be appropriate for a child's developmental stage, learning opportunities must be purposeful, meaningful and problem-oriented 20 .
- Education should be focused and interesting for children. This can be achieved by incorporating learning moments into a structured game (for example, playing a dice game can help children learn to recognize numbers from one to six). Music and drawing can serve as natural aids to bring attention to patterns, numbers, and shapes (eg, maintaining a two- or three-clap rhythm; drawing a number of balloons).
Parents and educators can use numerous daily situations to teach (for example, "How many feet do you have? ... So, how many socks do you need to get out of the drawer?"). Children's questions can be an important source of purposeful learning. - Learning should be meaningful for children and gradually build on (and connect with) what they already know. For adults working with 2-year-olds, a significant goal is to teach children to recognize the number "two". You should not be too hasty in teaching children about subsequent numbers, such as the number "four", as this may reduce their motivation (the child may become inattentive or aggressive, give answers inappropriately, or otherwise withdraw from the activity).
- Teaching should be, as far as possible, problem-oriented or thought-provoking. Instead of just giving children some information, parents and educators should give children the opportunity to think about a problem or problem, make assumptions (thoughtful guesses), develop their strategy, or deduce their answer.
Cases of Alice 21 and Lucas 22 illustrate some of the aspects described above:
- Case of Alice. By the age of two and a half, Alice was already able to confidently distinguish one, two or three objects. Therefore, her parents wanted to expand the range of the girl's knowledge to the number "four", which at that time was beyond her capabilities. Instead of just saying the number "four" when describing groups of four, they asked Alice questions about such groups. The girl often answered, having previously divided the unfamiliar group into two acquaintances. Then her parents completed her answer: "Two plus two equals four." When Alice was shown a picture of four puppies at 30 months of age, she placed two fingers of her left hand on two puppies and said, "Two." Without removing her left hand, she placed two fingers of her right hand on the other two puppies and said, "Two." She then used the statement she learned from her parents that "two plus two equals four" to indicate the cardinal number of puppies in the painting.
- Case of Lucas. In the context of a computer math game, Lucas was presented with the example 6+6. He determined the amount using the account. Then he was shown an example of 7 + 7. He smiled and quickly replied, "Thirteen." When the computer announced the correct answer, the number 14, Lucas looked puzzled. After a couple of tasks, he got an example of 8 + 8, and Lucas explained: “I was going to answer 15, because 7 + 7 was 14. But before that, 6 + 6 was 12, and I thought that 7 + 7 is probably 13, but was 14. So I'm going to answer that 8+8 is 16."
Future Directions
Much remains to be learned about the development of math skills in preschoolers. Does Verbal Number Recognition at Age Two Affect Kindergarten Readiness and Math Performance in School? If so, can an intervention based on relevant and irrelevant examples help children at risk of achievement to catch up with their peers? What other well-formed concepts or skills can predict kindergarten readiness or school math performance in two- to three-year-olds? How effective are the programs currently being developed for early mathematical development?
Conclusions
Contrary to the opinion of many preschool teachers, teaching mathematics to children at the age of two makes sense 23,24,25,26 .
As shown in Figure 1, this training should begin with the development of children's understanding of "intuitive" cardinal numbers, as well as the skill of recognizing and labeling groups of one to three objects with the corresponding numerals. As shown in Figure 1, this knowledge of numbers is key to the subsequent development of numeracy, and children with math difficulties may often lack it 27 . Early learning does not mean that preschoolers will be bombarded with a huge amount of information and forced to practice with flashcards and memorize arithmetic examples. In order to develop children's sense of numbers and fluency in elementary calculations, help children identify relationships and patterns, and encourage them to invent their own reasoning strategies.
Figure 1. Learning trajectories for some key numerical, counting and arithmetic concepts and skills
The studies described were supported by a grant from the National Science Foundation (BCS-0111829), the Spencer Foundation (mega-grant 200400033), the National Institutes of Health (1 R01 HD051538-01), and the Institute of Education and Science (R305K050082) .
The views expressed in this manuscript solely reflect those of the author and do not necessarily reflect the position, policy, or endorsement of the aforementioned institutions.
Literature
- Baroody AJ, Dowker A. The development of arithmetic concepts and skills: Constructing adaptive expertise. In: Schoenfeld A, ed. Studies in mathematics thinking and learning series . Mahwah, NJ: Lawrence Erlbaum Associates; 2003.
- Kilpatrick J, Swafford J, Findell B, eds. Adding it up: Helping children learn mathematic s. Washington, DC: National Academy Press; 2001.
- Baroody AJ, Lai ML, Mix KS. The development of number and operation sense in early childhood. In: Saracho O, Spodek B, eds. Handbook of research on the education of young children . Mahwah, NJ: Erlbaum; 2006: 187-221.
- Clements D, Sarama J, DiBiase AM, eds. Engaging young children in mathematics: Standards for early childhood mathematics education .
Mahwah, NJ: Lawrence Erlbaum Associates; 2004: 149-172. - Ginsburg HP, Klein A, Starkey P. The development of children’s mathematical knowledge: Connecting research with practice. In: Sigel IE, Renninger KA, eds. Child psychology in practice . 5th Ed. New York, NY: Wiley & Sons; 1998; 401–476. Handbook of child psychology , vol 4.
- Baroody AJ. Why children have difficulties mastering the basic number facts and how to help them. Teaching Children Mathematics 2006;13:22–31.
- Baroody AJ, Thompson B, Eiland M. Fostering the fact fluency of grade 1 at-risk children. Paper presented at: The annual meeting of the American Educational Research Association. April, 2008. New York, NY.
- Gersten R, Chard, D. Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. The Journal of Special Education 1999;33(1):18–28.
- Jordan N.C. The need for number sense. Educational Leadership 2007;65(2):63–66.
- Dowker AD. Individual differences in arithmetic: Implications for psychology, neuroscience and education . Hove, England: Psychology Press; 2005.
- Baroody AJ. The development of kindergartners' mental-addition strategies. Learning and Individual Differences 1992;4:215-235.
- Baroody AJ, Eiland M, Thompson B. Fostering at-risk preschoolers' number sense. Early Education and Development 2009;20:80-120.
- Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal processes in early quantitative development. In: Kail R, ed. Advances in child development and behavior , vol 33. New York, NY: Academic Press; 2005: 305-346.
- Baroody AJ, Li X, Lai ML. Toddlers' spontaneous attention to number. Mathematics Thinking and Learning 2008;10:1-31.
- Dehaene S. The number sense . New York, NY: Oxford University Press; 1997.
- Wynn K.
Numerical competence in infants. In; Donlan C, ed. Development of mathematical skills . Hove, England: Psychology Press; 1998: 1-25. - Benoit L, Lehalle H, Jouen F. Do young children acquire number words through subitizing or counting? Cognitive Development 2004;19:291–307.
- Baroody AJ, Lai ML, Li X, Baroody AE. Preschoolers' understanding of subtraction-related principles. Mathematics Thinking and Learning 2009;11:41–60.
- Mazzocco M, Thompson R. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice 2005;20:142-155.
- Baroody AJ, Coslick RT. Fostering children's mathematical power: An investigative approach to K-8 mathematics instruction . Mahwah, NJ: Erlbaum; 1998.
- Baroody AJ, Rosu L. Adaptive expertise with basic addition and subtraction combinations: The number sense view. In: Baroody AJ, Torbeyns T. chairs. Developing Adaptive Expertise in Elementary School Arithmetic.
Symposium held at: The annual meeting of the American Educational Research Association. April, 2006. San Francisco, CA. - Baroody AJ. Fostering early number sense. Keynote address at: The Banff International Conference on Behavioral Science. March, 2008. Banff, Alberta.
- Baroody AJ, Li X. Mathematics instruction that makes sense for 2 to 5 year olds. In: Essa EA, Burnham MM, eds. Development and education: Research reviews from young children . New York: The National Association for the Education of Young Children; 2009: 119-135.
- Bredekamp S, Copple C. Developmentally appropriate practice in early childhood programs. Washington, DC: National Association for the Education of Young Children; 1997.
- Copley J, ed. Mathematics in the early years, birth to five . Reston, VA: National Council of Teachers of Mathematics; 1999.
- Copley J, ed. The young child and mathematics. Washington, DC: National Association for the Education of Young Children; 2000.
- Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8-9 year old students. Cognition 2004;93:99–125.
This article was originally published in the Encyclopedia of Language Development and Literacy by the University of Western Ontario, who owns the copyright to this article.
in Russia, an instant learning method was created for pattern recognition
The indexron algorithm (hereinafter referred to as indextron) needs only one photo to learn to recognize the desired object, while an artificial neural network requires thousands of images for this. Experiments of scientists of the Institute of Control Problems. V. A. Trapeznikov RAS (IPU RAS) confirmed that even after such a short “instruction”, the indextron successfully recognizes objects regardless of their scaling and rotation and with their significant deformations.
Indextron is a Russian invention, which has no analogues in the world.
The creator of this algorithm, senior researcher at the Laboratory of Technical Diagnostics and Fault Tolerance, Ph.D. Alexei Mikhailov published back in 1998. Since then, this algorithm has been tested in a wide variety of applications: it analyzed gamma-ray telescope signals, classified vegetation from satellite images, navigated images of the lunar surface, and also found use in fingerprint identification, trademark recognition, and even checked the compositions of schoolchildren. . Now, specialists from the IPU RAS have tested it in solving the most difficult task - recognizing objects taken from different angles, at different distances and against an arbitrary background.
Automatic recognition of three-dimensional images on flat images is a difficult task that is being solved today with the help of artificial neural networks. Neural networks imitate the principle of operation of brain neurons, however, they have not yet been able to compare with the human mind in the efficiency and speed of pattern recognition.
A person instantly distinguishes a rose from a cat, and it takes a long time for an artificial neural network to learn this.
“The main problem associated with artificial neural networks is the problem of learning,” says Alexei Mikhailov. “For learning, that is, the adaptation of neural networks to different applications, it is required to find a large number of coefficients with which the network is tuned to a particular task, and to find these coefficients, a large amount of calculations is required.”
This problem, according to the scientist, is exacerbated by the difficulty of identifying features by which this or that object is recognized. Previously, this was done “manually” by trial and error, that is, the person himself invented what signs to use to recognize the cat. It could be, for example, the length of the ears, stripes on the coat, the distance between the eyes, etc. After that, the neural network is tuned using coefficients for this feature and look at the result.
Then another feature is tried, and such a selection can continue for quite a long time. This is inconvenient, therefore, 15 years ago, the so-called deep machine learning appeared, when many layers of neurons are used - 100 or even more, which allows you to work with "raw" features - for example, with pixels of depicted objects.
“With deep machine learning, you don't have to invent anything,” says Alexey Mikhailov. - The algorithm itself generates selection criteria based on "raw" features. Deep learning is very popular right now, but it solves the problem of automating feature discovery by using more and more coefficients. After all, each layer means new coefficients.”
Finally, there is another problem: training a neural network requires a huge amount of data. The network must analyze thousands of photos of a cat in order to learn to recognize it. The algorithm proposed by Russian scientists also works with “raw” features in the form of pixels, but at the same time it does not need to calculate any coefficients, and a pair, and sometimes even one photo, is enough for training.
“The algorithm is an index classifier, called indextron for short,” says the scientist. - It uses the same principle of operation as the Google search engine. This is a very simple and convenient thing, which can later be implemented as a chip.”
The pedigree of this invention is interesting. If neural networks originate from the Rosenblatt perceptron (a cybernetic model of the brain implemented in 1960 in the form of the world's first neurocomputer "Mark-1" by the American scientist Frank Rosenblatt), then the indextron and its close relative the Google search engine originate from the book index, the very one that can be found at the end of some books, where by keywords you can immediately find the page where they occur.
Index search in Google is carried out by working with inverse documents. A document is a set of words, and a reverse document is a list of documents that contain the keyword typed in the search string, after which Google almost instantly provides links to all pre-indexed documents that contain the word or several words from the search query.
“Indextron works very similarly, but if the Google search engine works with textual information, then indextron works with numbers,” explains Alexei Mikhailov.
Any image can be considered a document consisting not of words that form sentences, but of graphic elements that form an image. A word is made up of letters, and a graphic image is made up of pixels. Each pixel can be represented digitally, where each of its colors - red, green and blue - has 256 brightness levels. Thus, each pixel is translated into three numbers, and then the indextron works with this data.
Fig. 1. On the right are two photographs of objects Rose and Cat, on which the indextron was trained. The algorithm digitizes pixels by the red, green, and blue color components of each pixel, and then extracts the pixel classes that characterize these objects. The frequency with which the pixels of these classes occur in the image serves as a sign of recognition. The histogram on the left shows how strikingly different are the class frequency distributions for these two objects.
In a simplified form, the operation of the indextron looks like this: the image of a cat is characterized by a certain set of pixels, just as the word "cat" is characterized by a certain set of letters. Indextron can select a set of numbers that characterizes the image of a cat from one photograph. Learning happens almost instantly. And if the same characteristic set of numbers is found in another photograph, then the indextron recognizes a cat in it.
Fig. 2. Comparison of the "digital signatures" of the Rose object in the images taken from different angles. The number of common features is 7.
The Google search engine does not think about the meaning of the word "cat", it simply indexes the documents containing it. But indextron does not index images, but objects with the help of sets of numbers characterizing the desired images. Therefore, it does not matter which image will be presented to the system. If the image contains a cat, it will be recognized.
Thus, the search engine becomes a recognizer.
“The human brain consists of rational and emotional parts,” says Alexei Mikhailov. “Intelligence is in the cerebral cortex, and emotions are in the brain stem at its center, but the brain is not a computer. He doesn't do calculations. There is an assumption that it is the indexing of images, and not calculations, that underlies biological recognition systems, and the cerebral cortex is an index system in which images are described by a combination of addresses. This explains the speed of the brain in the tasks of image recognition. The neurons of the brain operate at frequencies below 500 Hz, while the clock frequency of computers reaches billions of hertz - several MHz, but still the brain begins to recognize a stranger from the first meeting, that is, it can instantly learn.
Fig. 3. Comparison of "digital signatures" of images of the Cat object in different photographs. The number of common features is 6. The object is recognized despite a different angle, body position, and a tucked tail.
Indextron was trained on two different objects (a flower and a cat). Moreover, the training was carried out using only two images. For testing, the same objects were shown from different angles: 10,000 test images were classified using a four-layer neural network and an indextron.
It took 900 seconds to train a four-layer neural network to recognize a cat or a rose in an image. At the same time, in addition to the AMD Ryzen 5 3600 processor, the Nvidia GeForce GTX 1600 Super graphics card was used. It took only 16 s to train the indexron. In this case, the same processor was used, but without a video card. As a result, the four-layer neural network showed an object identification accuracy of 85.3%, and indextron - 82.87%.
Fig. 4. The capabilities of the indextron were also tested when recognizing objects such as a car. On the left is a photograph of the training. On the right is a test photo. The car was recognized despite a completely different angle.
