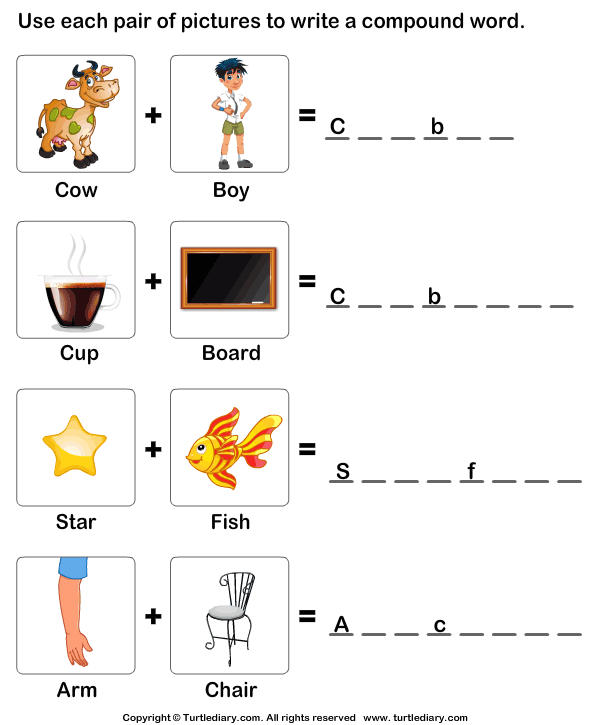
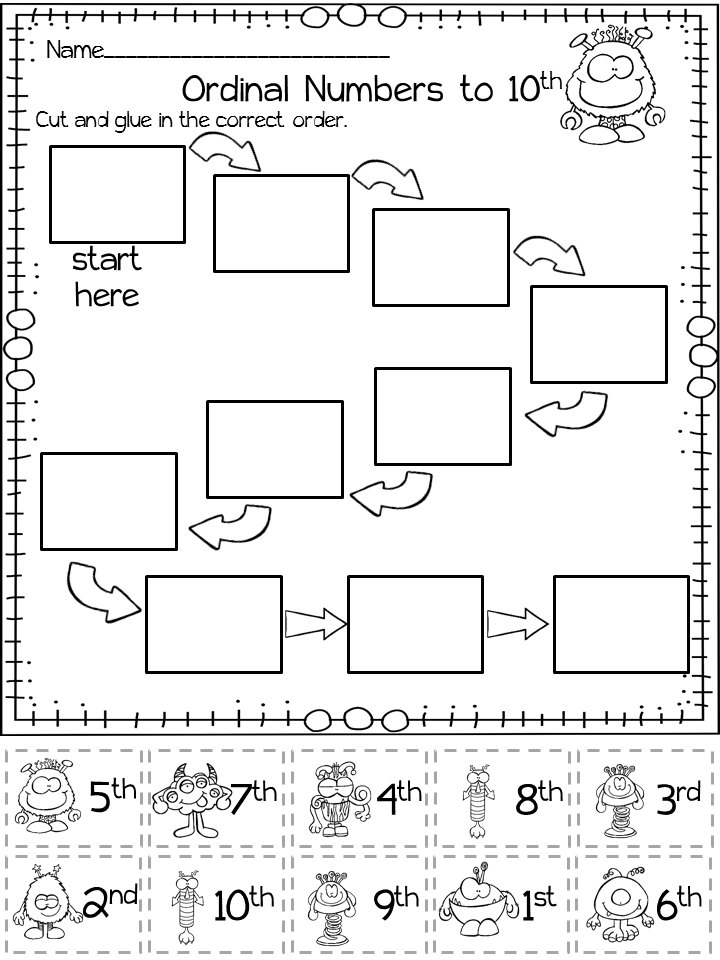
Ordinal numbers activities for kindergarten
10 Free Ways to Teach This Skill
This post contains affiliate links. If you click & make a purchase, I receive a commission at no additional cost to you! Thanks! As an Amazon Associate, I earn from qualifying purchases. Read my full disclosure here.
Ordinal numbers are a concept that we use every single day. So, obviously, we need to make sure that our kids understand what they are and what they mean. But, you may be thinking, “It’s been a few years since I was in school, and I can’t remember what the heck an ordinal number is!”
Well, don’t worry because I’m going to tell you what they are, and I’m going to share 10 ordinal numbers activities to help you teach this skill across all the different subjects!
What are Ordinal Numbers?
Ordinal numbers are simply “a thing’s position in a series.” (As in, first, second, third, so on and so forth.) That’s it!! Yet, understanding what they are in your mind and knowing how to explain ordinal numbers to kids are entirely different.
You can say, “one” and show a child one object. That’s pretty straightforward.
However, ordinal numbers are relational and a completely abstract concept to little kids.
What I mean is that the relationship between the positions of 2 different objects is the foundation of ordinal numbers. In other words, you have to have a second to have a first.
That’s why you need engaging activities and ordinal number exercises that provide a solid foundation! But, don’t think you have to learn all sorts of new information. It’s very likely that you’re already doing some and don’t even realize it.
So, let’s get to it!
Ordinal Numbers Activities
1. Line It Up
One of the first and easiest ordinal number activities for preschool is lining objects up in a row. My favorite thing about this activity is that you can use anything of which you have an abundance. (So, at our house, we would use LEGOs because we own about 10,000 LEGO bricks.)
You can use stuffed animals, cars, trains, or any other objects that interest your kiddos.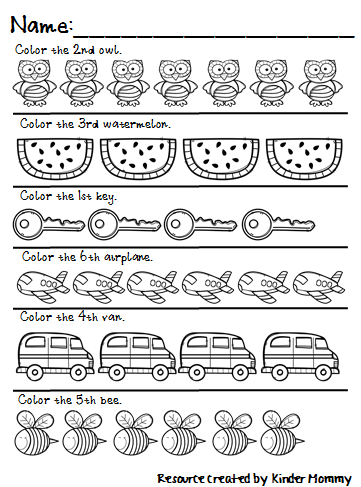 Start out with 3-5 objects and my free printable ordinal number cards. Let your kiddos point to the object and match the correct number card. It’s that easy!!
Start out with 3-5 objects and my free printable ordinal number cards. Let your kiddos point to the object and match the correct number card. It’s that easy!!
As a classroom teacher, you can extend this lesson by having your students line up. However, there is a trick to this. Make sure to take a picture of everyone in the line, and then show the image to the class. Otherwise, everyone will be stepping out of line to see the first person, Jimmy won’t be able to see around Susie, and pushing will ensue. Trust me, classroom management will be a nightmare.
Print out several sets of the image and ordinal number cards. Then have your students work together to match the student and the position. (Joey is first. Cindy is second.)
2. Days of the Week
Another one of my favorite ordinal number activities is using the days of the week. If you do any sort of calendar time, you may already be teaching them without even knowing it! You probably say something along the lines of, “Sunday is the first day of the week. Monday is the second day of the week.”
Monday is the second day of the week.”
If not, just start doing this daily. You’ll be amazed at how the consistent practice helps. If you want visuals to go along with the sentences, I have a free “Days of the Week” printable you can use with your ordinal number cards.
See how easy this is? You can do it!
3. Months of the Year
This is another quick way to practice ordinal numbers on a day-to-day basis. When you are discussing the current month, use my free printable months of the year pages to show the position of each month.
Just print out the months and point to the current month. Let’s say we are in the month of March, point to March and say, “This is March. It is the third month of the year.” Then you can write 3rd beside March. Continue this same cycle of sentences and discussion until you have talked about every month and practiced the concepts of first through twelfth.
4. Sequencing
Remember, teaching ordinal numbers doesn’t have to be super-complex. By simply talking about consistent, sequential daily activities, you are teaching ordinal numbers. Think about it like this. What are the events that kids do every day? First, wake up. Second, put on your clothes. Third, put your pajamas away. Fourth, eat breakfast.
By simply talking about consistent, sequential daily activities, you are teaching ordinal numbers. Think about it like this. What are the events that kids do every day? First, wake up. Second, put on your clothes. Third, put your pajamas away. Fourth, eat breakfast.
See? You don’t need an expensive set of sequencing cards. You can either draw pictures or let your child draw them. Just have your kids put the pictures in order and match the ordinal number cards to them! Easy peasy.
5. Following Recipes
Following recipes is another one of my favorite ordinal number activities. Obviously, you need to use your judgment on the intricacy of the recipe, but for young children let them make something like pudding.
Go ahead and have all of the tools out for them. Then allow them to complete the steps as independently as they can. For those just learning the concept of ordinal numbers, let them complete 3 steps. “First, pour in the pudding mix. Second, pour in 2 cups of milk. Third, stir it all together.”
Third, stir it all together.”
For older kids, let them give you a running commentary on every step. “First I get out my bowl. Second, I get out the pudding mix and milk. Third, I pour the pudding mix into the bowl.”
To extend this activity, you can allow them to video themselves and then write the sequence into their own written recipe. Think about what a fun family activity this would be! Your kids could make an entire cookbook and then give them to family members as Christmas gifts.
By the way, I recently found a recipe that I had written when I was in second grade, and it should have been a foreshadowing to my future issues with cooking. I was able to explain (in detail) how to cook “spasketty” in 3 steps. It was hilarious! Obviously, my understanding of cooking and ordinal numbers wasn’t really vast.
6. ABC Order
This is a great way to combine reading and math! You can either make your own alphabet flashcards with index cards and a sharpie or get a pack of simple alphabet flashcards. Then let your littles match the first 12 letters of the alphabet with the appropriate ordinal number. You can mix them up to make it more challenging for your more advanced learners.
Then let your littles match the first 12 letters of the alphabet with the appropriate ordinal number. You can mix them up to make it more challenging for your more advanced learners.
To add another level of difficulty, have your kids write their spelling words or vocabulary words and cut them out. Then have them mix the words up and put the words into alphabetical order while matching the correct ordinal number. This is another one of my favorite ordinal number activities!
7. Sports
If you have a child that loves sports, then get them thinking about how each sport makes use of ordinal numbers. Here are two examples…
- Football-1st, 2nd, 3rd, 4th downs: 1st-4th quarters: rankings of the favored teams in the NFL
- Baseball-1st, 2nd, 3rd base: 1st-8th innings: rankings of the favored MLB teams
This is extremely useful when you get the dreaded “When am I ever going to use this skill in real life?” Well, now they know!!
8. Competition
Because I’ve taught boys, and am raising two boys of my own, I am keenly aware of how much they love competition. They can make a competition out of literally ANYTHING.
They can make a competition out of literally ANYTHING.
So, take advantage of this and let them compete in any category they want. Then have them give out the prizes to the appropriate winner. (Depending on how many participants, you may be able to give out all 12 of the ordinal number tags.)
Any time you can make learning into a game, you have a winning combination.
9. Order of Events
If you have older kids, they will be required to understand and create timelines. So, this is the perfect opportunity to incorporate math into history!
There is a distinct relationship between historical events and ordinal numbers, and this is a great time to get kids thinking about that fact. Have them write out several significant events from history, mix them up, and then ask them to put the events into order.
To challenge your kiddos even more, ask them to explain the cause and effect relationship between the events. This gets them thinking more deeply about “why” the events happened in that specific order.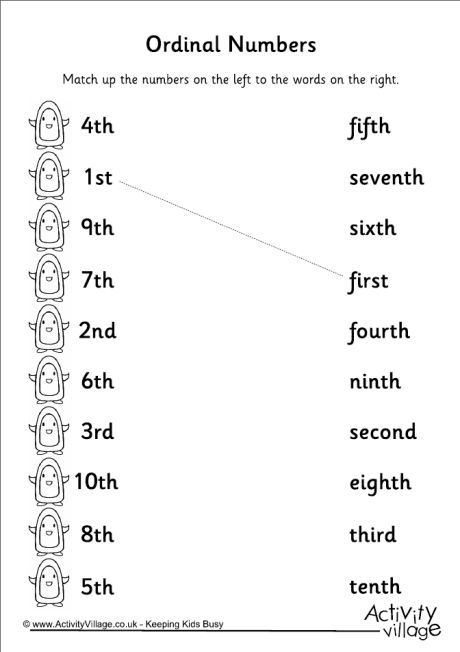
10. Paragraph Structure
We all know the importance of good writing, but sometimes we don’t really know what that looks like at different levels. Honestly, it can be pretty tricky, but one thing that is necessary to good writing is the use of ordinal numbers! (I bet you knew I was going to say that.)
Think of it like this, if you want your kids to be able to have a coherent piece of writing, they need to include a sequence of events or a distinct order to their paragraphs. So, you teach them how to write sentences and put those sentences into order. “First, the man gave the dog a bone. Second, the dog dug a hole to hide the bone.”
Then when they’ve mastered that skill, you apply this same technique to creating paragraphs and essays!
So, there you have it!
Ten activities for teaching ordinal numbers in all content areas, and all of them are completely FREE!! Was it easier than you thought it was going to be? Do you think you can use some of these simple ideas?
Definition And Activities For Kids
Learning mathematical skills is a vital part of early childhood development. And understanding ordinal numbers and how they work is part of building this competency.
And understanding ordinal numbers and how they work is part of building this competency.
Before we dive deeper into what ordinal numbers are and how you can assist your child with learning them, it’s important to know that we use them in our everyday lives.
This means your child has probably already come across this numerical concept, even though they may not know how to put it into words yet.
To help your young learner reach a stage where they fully comprehend and can use these numbers correctly, we’ve prepared five effective activities for you to try at home.
Let’s begin!
What Are Ordinal Numbers?
Ordinal numbers help us communicate the order of objects in a series. For example, first, second, third, and so on.
In theory, this sounds easy, but explaining it to children can be a little challenging. For instance, you can show a child the number “2,” and they may be able to understand what it means to have two of something (e.g., two eyes, two ears).
But when we talk about ordinal numbers, second (the ordinal number) is very different from two (the integer).
That’s because these numbers are not just about counting — they are more about things in relation to one another. And we have to look at a whole series or set for us to determine which object is first, second, third, etc.
The good news? Most children come across these types of numbers when watching a race or playing a game. They may be able to say:
Tommy came first.
Suzi was second.
Lorna was third.
Mike was last.
Children also spend a lot of time working with ordinal numbers in their early years at school because they connect with other critical mathematical concepts, such as sequencing and counting. So, helping your child understand them is part of a good foundation.
How Do You Write Them?
There are many different ways to write numbers, depending on what you are trying to show or solve.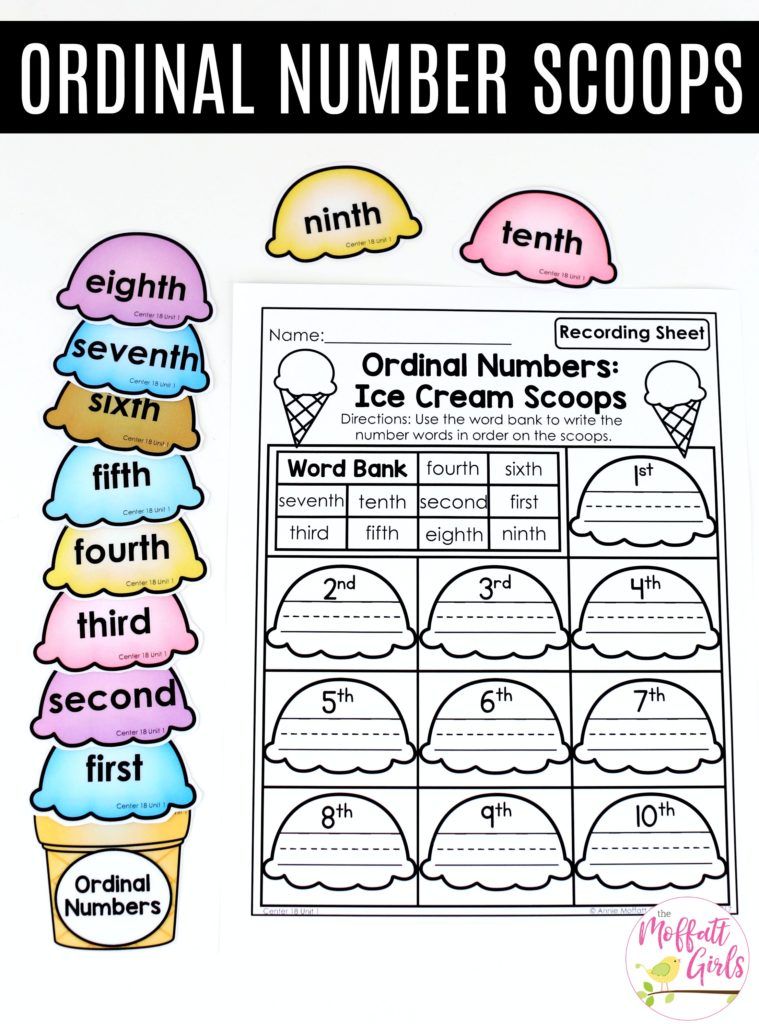 In the case of ordinal numbers, here are a few things to consider.
In the case of ordinal numbers, here are a few things to consider.
Let’s take a look at the first 10 ordinal numbers:
- First (1st)
- Second (2nd)
- Third (3rd)
- Fourth (4th)
- Fifth (5th)
- Sixth (6th)
- Seventh (7th)
- Eighth (8th)
- Ninth (9th)
- Tenth (10th)
From the above list, you can see that we write ordinal numbers by using the last two letters of the word. For example, fifth = 5th.
When looking at compound numbers, we apply the following:
- Numbers ending with 1: Only add “st” (e.g., twenty-first = 21st, thirty-first = 31st)
- Numbers ending with 2: Only add “nd” (e.g., twenty-second = 22nd, thirty-second = 32nd)
- Numbers ending with 3: o/Only add “rd” (e.g., twenty-third = 23rd, thirty-third = 33rd)
- Numbers ending with 4, 5, 6, 7, 8, 9, or 0: Only add “th” (e.g., twenty-fourth = 24th, thirty-fifth = 35th)
Some people add “ly” at the end of an ordinal number when it’s written out (e. g., firstly, secondly, thirdly, etc.). However, when dealing with larger numbers (from 9th upwards), it’s best to avoid the “ly” altogether.
g., firstly, secondly, thirdly, etc.). However, when dealing with larger numbers (from 9th upwards), it’s best to avoid the “ly” altogether.
Ordinal Vs. Cardinal Numbers
We can’t look at ordinal numbers without also identifying what cardinal numbers are and how they relate.
In a nutshell, cardinal numbers tell us how many there are of something. For example, you have two ears. We also use these numbers for counting. Ordinal numbers, on the other hand, tell us the order of things in a set. For example, Timothy is second in the line.
Distinguishing between these two concepts can sometimes be tricky, especially for young learners. For instance, they might say, “The number three question was so easy,” instead of, “The third question was so easy.”
Activities are a great way to help our children identify the differences between these two concepts. With that in mind, here’s our list of five fun and effective games you can play with your child at home!
5 Activities To Learn Ordinal Numbers For Kids
1) Toy Lineup
What You’ll Need:
- Index cards
- Marker
- Any toys of your choice
What To Do:
The simplest way to introduce ordinal numbers to children is by placing some of their favorite toys in a line.
For this activity, you can use anything — dolls, toy cars, trains, legos — basically, anything you have an abundance of. After placing these items in a line, write ordinal numbers on your index cards (one number on each card).
To start playing, hand your child the index cards. Then, have them match the correct number card with each toy. For example, if they point at the fourth toy, they need to show you the card labeled “4th.”
You can start with just three to five items and, as they improve their skills, increase the line to 10 items or more.
This is a great way for children to get comfortable with what ordinal numbers look like in their numerical form.
2) Change The Lineup
What You’ll Need:
- Index cards
- Marker
- Any toy of your choice
What To Do:
As the name suggests, this activity is all about changing the positions of your lined-up objects. You can use the same toys you used in the previous game.
Start with changing the position of one object. For example, move one item from the third to the last spot. Then, ask your child:
For example, move one item from the third to the last spot. Then, ask your child:
Which toy is third in line now?
Which toy is last in line now?
Continue moving just one object at a time, and encourage your child to re-evaluate their positions.
This game allows children to grasp that just one change is enough to influence the whole series. It also encourages them to think beyond memorization. As you switch things up, they’ll have to focus on which object is now the first, second, third, and so on.
3) Story Plot Map
What You’ll Need:
- A sheet of paper
- Marker
What To Do:
To begin, draw four boxes on your sheet of paper and label them with ordinal numbers (1st, 2nd, 3rd, and 4th). Next, tell a story in parts. For example, it might look something like this:
First, a girl named Emily wanted to get a cat.
Second, she went to a store and found the cutest little kitty.
Third, she asked her parents to get the cat.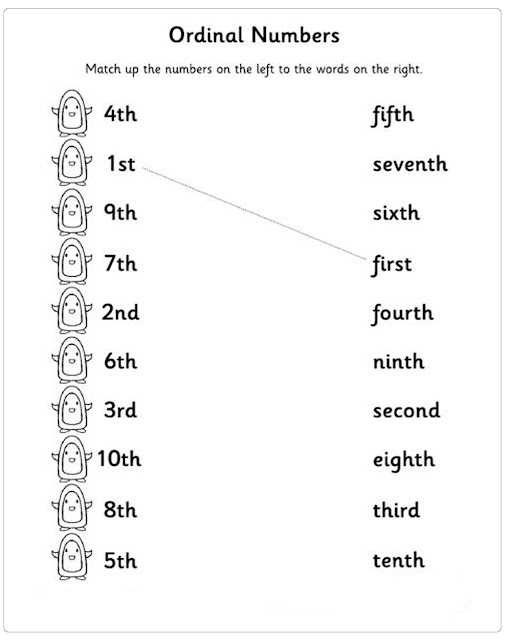
Fourth, they told her…
You can also write (or help your child write) what happens in each box as you tell the story. (So, “First, a girl named Emily wanted to get a cat” would go in the box labeled “1st”).
Point to each box as you tell that part of the story to give a visual representation of the events and emphasize the ordinal numbers (e.g., first, second, and so on).
Your story can take any direction you wish, and you can also encourage your child to give their input on what happens next.
One challenge with this game is ending the story on the last box. If there are four boxes, for example, then the fourth has to end it all. We recommend beginning by modeling all four boxes yourself first.
After that, your child thinks of box one, you get box two, they get box three, and you conclude the story for box four. After trying this a few times, let your child try the fourth box.
4) Color The Rainbow
What You’ll Need:
- White sheet of paper
- Pencil
- Crayons
What To Do:
Start by drawing eight lines in the shape of a rainbow on your sheet of paper. Then, hand the paper to your child. To play, have them listen to and follow directions as you tell them which stripe to color in.
Then, hand the paper to your child. To play, have them listen to and follow directions as you tell them which stripe to color in.
For example:
Color the third stripe green.
Color the fifth stripe orange.
Continue giving instructions until the rainbow has all of its seven colors.
Don’t be surprised if your child has to count each time they color in a stripe. This is all part of practicing and learning as they go, and this activity reinforces that ordinal numbers are about looking at the order of a whole set.
5) Wrong Order
What You’ll Need:
- Index cards
- Marker
What To Do:
Start by writing 1st-10th down on your index cards (one number on each card). Then, shuffle the cards and line them up in the wrong order. Very simply, the object of the game is for your child to place the cards in the correct order.
They might need a little help in the beginning, but as they get more comfortable, you can add a timer to keep things interesting: Let’s see if you can line these up in their correct order in under 30 seconds!
This is a great activity for children to practice identifying ordinal numbers in their numerical form (1st, 2nd, 3rd, etc. ).
).
Ordinal Numbers Are Not So Ordinary!
While we may use the concept and language of ordinal numbers every day, there’s nothing ordinary about them.
And as you can now see, helping children learn to correctly identify these numbers is crucial because they form part of other important concepts, such as sequencing. The above activities allow your child to work on and solidify their knowledge of ordinal numbers with you at home.
In addition, our Wacky Slide game from the HOMER Learn & Grow app is specially designed to help reinforce the fundamentals of understanding and working with ordinal numbers.
By using these activities — and with lots of time and practice — your young learner will be an ordinal number pro in no time!
Author
Consultation for educators on the topic: “Teaching children quantitative and ordinal counting”
Plan
- Counting items.
- Concepts of quantitative and ordinal numbers.
- Methods of familiarization with the ordinal and quantitative value of a number in kindergarten.
- Job examples.
How often do we ask a child the following questions: How old are you? How many friends do you have? How many paws does a cat have?
To calculate all this, you need to know the numbers.
Have you ever wondered where the numbers came from? Primitive people, as well as modern children, did not know the account. Children are now being taught, but there was no one to teach primitive people. Life taught them. Observing the surrounding nature, on which he was completely dependent, he learned to single out individual objects. From a pack of wolves - a leader, from an ear - one grain. At first, they defined this ratio as one-many. Frequent observations of a set consisting of a pair of objects (eyes, ears, arms, legs, wings) led a person to the concept of a number. Our distant ancestor, when he saw a pair of ducks, he compared them to a pair of eyes. And if he saw more, he said "a lot." Only gradually did a person learn to distinguish three objects, and then 4, 5.
Our distant ancestor, when he saw a pair of ducks, he compared them to a pair of eyes. And if he saw more, he said "a lot." Only gradually did a person learn to distinguish three objects, and then 4, 5.
Numbers were invented by people for counting, as well as for fixing the results of measuring values.
When extracting prey, exchanging it for objects of their labor, ancient people showed the required number on their fingers. Traces of counting on the fingers have been preserved in many countries. For example, in China and Japan, household items are counted not in dozens, but in fives and tens.
After the concept of number was formed, numbers became independent objects of science "mathematics" and it became possible to study numbers and actions with them. The science that studies numbers and actions with them is called "arithmetic" (translated from Greek as number).
Each set is equivalent to only one number. Since the number means a quantitative characteristic, I call it quantitative.
In quantitative counting, the result does not depend on the order in which the elements were counted. It is only important not to skip elements when counting and not to count the same element twice. A quantitative account answers the question, "How much?"
When counting the elements of a set, they are numbered. Counting is the process of ordering a set by assigning a specific number to each element of the set. In this case, a natural number denotes its serial number of some element and is called - ordinal.
With ordinal counting, the result depends on the sequence in which the elements were counted. The ordinal account answers the question: “Which one?”
Counting is the process of numbering the elements of a set. This process is subject to certain rules:
- the first marked item is assigned the number 1;
- at each next step, an object not yet marked before is selected;
- he is assigned the number following the next of those already named.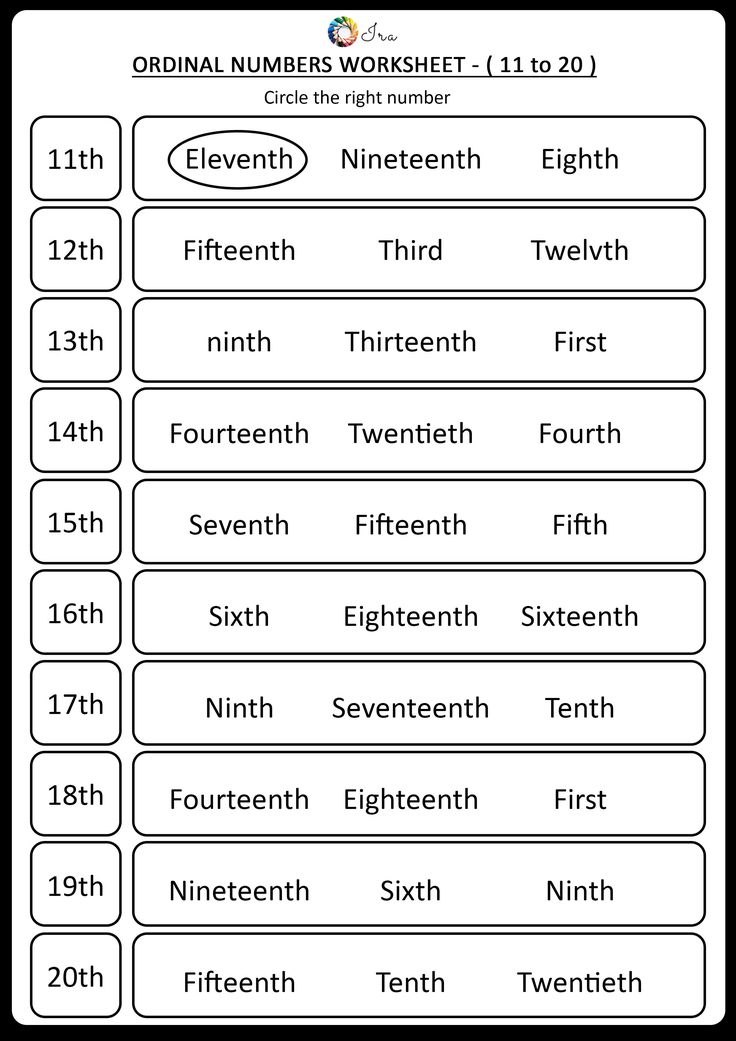
It is based on the principle that each subsequent number, starting from the second, is one more than the previous one.
After the child has learned to count, that is, knowledge of counting means knowing the words of numerals, the names of their order in counting, understanding the meaning of the process of numbering objects, you need to actively use the method of recounting any specific objects. This will allow him to correlate the name of the number with a certain object or group of objects, and determine the total number of objects. Understanding that the last called number is a characteristic of the quantitative composition of the set, and the ability to follow the rules of counting.
When mastering counting, a large load falls on mechanical memory, and not on a mental operation. In order for the child not to master it at a formal level, at first this process must be accompanied by objective actions: postponing, showing, and also speaking out loud.
When creating an account transaction, this task is useful.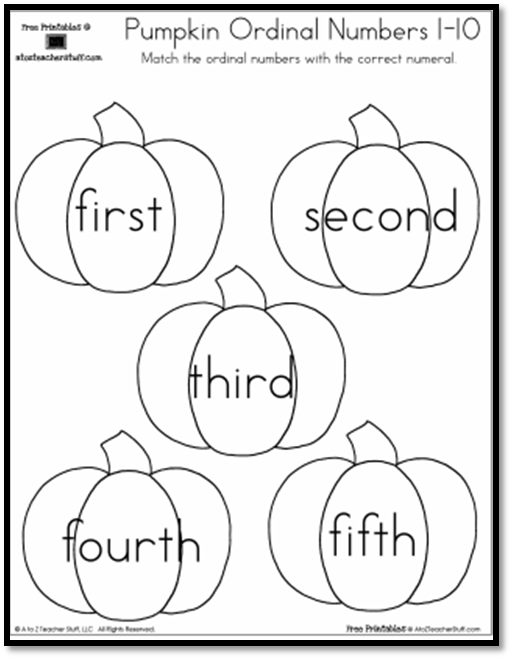 Count the circles on the flannelgraph so that the red circle is first, and now so that the red circle is second, last. With this exercise, the numbering process is not affected and therefore the child is not comprehended. Children unfamiliar with the above form of exercise usually ask: "Which side to count?" - and they are also trying to arrange objects in a row, being convinced that one can only count one can only count in such a position, and moreover, only from left to right. This shows that the process of counting in a child is formed only in a mechanical form and is not understood, not comprehended by him.
Count the circles on the flannelgraph so that the red circle is first, and now so that the red circle is second, last. With this exercise, the numbering process is not affected and therefore the child is not comprehended. Children unfamiliar with the above form of exercise usually ask: "Which side to count?" - and they are also trying to arrange objects in a row, being convinced that one can only count one can only count in such a position, and moreover, only from left to right. This shows that the process of counting in a child is formed only in a mechanical form and is not understood, not comprehended by him.
In the middle group of kindergarten, children were taught to count within 5. Consolidation of appropriate ideas and methods of action serves as a further basis for the development of counting activities. Much attention is paid to counting skills; children are taught to count objects, from left to right, pointing to the object in order, agree on numerals with nouns in gender number, name the result of the count. If someone does not understand the final value of the last number called when counting, then he is invited to circle the counted items with his hand. A circular generalizing gesture helps the child to correlate the last numeral with the entire set of objects. But in working with children of five years old, as a rule, it is no longer needed. Children now need to count objects at a distance, silently, i.e. inwardly. In the older group, memory for numbers begins to develop. When teaching five-year-old children the number of children, they are taught to see the independence of the number of objects from their spatial properties. Items may be different in color, in shape, but the quantity remains the same. Children of the older group are shown different methods of counting. They convince you that you can start with any object, and lead it in any direction, the main thing is not to skip objects when counting and not to count one object twice.
If someone does not understand the final value of the last number called when counting, then he is invited to circle the counted items with his hand. A circular generalizing gesture helps the child to correlate the last numeral with the entire set of objects. But in working with children of five years old, as a rule, it is no longer needed. Children now need to count objects at a distance, silently, i.e. inwardly. In the older group, memory for numbers begins to develop. When teaching five-year-old children the number of children, they are taught to see the independence of the number of objects from their spatial properties. Items may be different in color, in shape, but the quantity remains the same. Children of the older group are shown different methods of counting. They convince you that you can start with any object, and lead it in any direction, the main thing is not to skip objects when counting and not to count one object twice.
Change of didactic material, variation of tasks help children to better understand the methods of obtaining numbers and their quantitative composition.
In the older group, children are taught to use ordinal numbers. Five-year-old children use numerals, but they still use them not confidently and often not correctly. Therefore, it is necessary to reveal the meaning of ordinal numbers. To reveal the ordinal value of a number allows its comparison with a quantitative value. When they want to know how many objects they count: one, two, three, four, counting like this, they find the answer to question how much? But when you need to find the order, the place of an object among others, they think differently. Answering the questions: which? what's the score? count: first, second, third, etc.
Children often confuse questions which? and what? The latter requires the allocation of high-quality sv-in. items: color, size, etc. Interleaving questions: how much? which the? what's the score? which? Allows you to reveal their meaning.
Children have been shown more than once. What to answer question how much? It doesn't matter what order the items are counted in. Now they will learn that for determining the ordinal place of objects among others, the direction of the count is essential. The teacher demonstrates this by counting the same objects in different directions. He finds out, for example, that among 7 flags, blue is in fifth place, if counted from left to right, and if counted from right to left, then he is in 3rd place.
What to answer question how much? It doesn't matter what order the items are counted in. Now they will learn that for determining the ordinal place of objects among others, the direction of the count is essential. The teacher demonstrates this by counting the same objects in different directions. He finds out, for example, that among 7 flags, blue is in fifth place, if counted from left to right, and if counted from right to left, then he is in 3rd place.
Children try to determine the place of an object among others by counting in different directions. They conclude that when determining in which place the object is, it is necessary to indicate the direction of the account (third, fifth from the right, etc.).
Homogeneous objects that differ in color and size are used as counting material, for example, multi-colored flags and circles, Christmas trees of different heights, etc., and later - sets of objects of different types, for example, toys (characters of the fairy tale "Teremok", "Turnip ").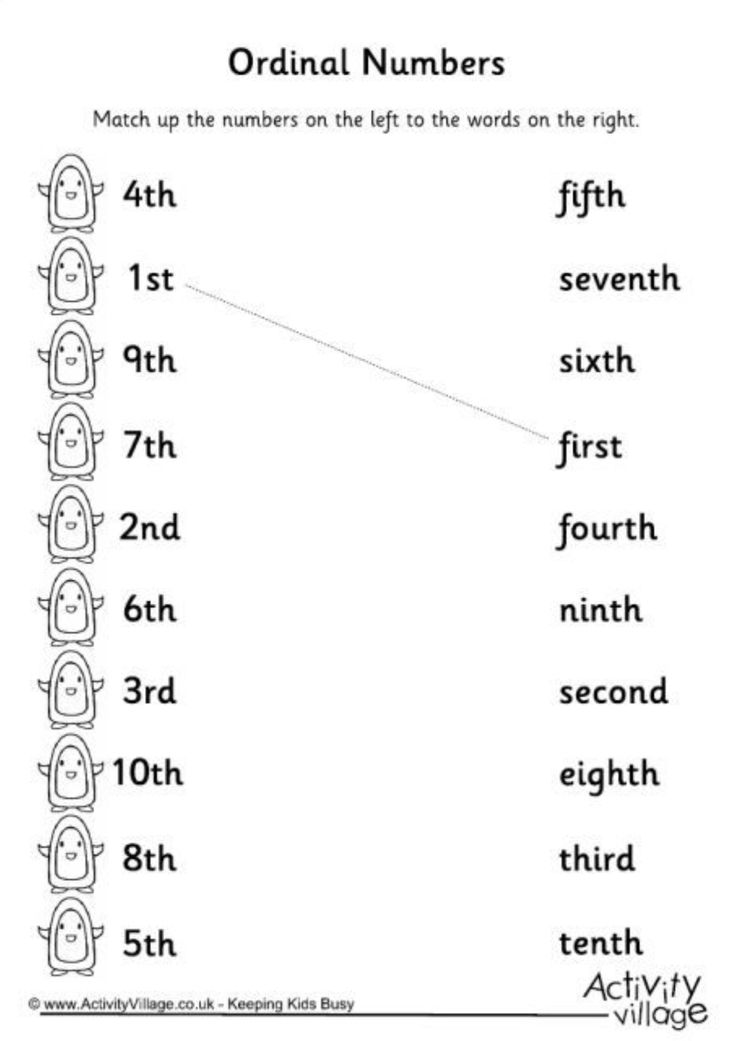 In ordinal counting, children are trained on plotless material, for example, on models of geometric shapes, stripes of different sizes, etc. Practicing in ordinal counting, they determine the place of an object among others, find an object that occupies a certain ordinal place (Which object is in first place, in third, fifth place?), Arrange objects in the specified order.
In ordinal counting, children are trained on plotless material, for example, on models of geometric shapes, stripes of different sizes, etc. Practicing in ordinal counting, they determine the place of an object among others, find an object that occupies a certain ordinal place (Which object is in first place, in third, fifth place?), Arrange objects in the specified order.
Some children, when determining the place of an object, replace ordinal numbers with quantitative ones. The teacher listens to how the children keep score, points out mistakes. Especially effective are the so-called combined exercises, in which the ordinal count is combined with the comparison of two or more sets of objects, the grouping of geometric shapes, and the ordering of objects by size.
Teaching ordinal counting is the main task of 3-4 lessons, in the future, ordinal counting skills are fixed in the course of working on new material.
M. Montessori suggests performing methodical exercises using one of the systems of bars as a didactic material.
Any day when the child lays out the sticks. You can offer to count the red sticks, blue sticks, start numbering from the red stick or from the blue stick. These exercises allow you to give the ordinal name of each stick: stick number one, second, etc. etc.
The ability to correlate a number, its name and sign is an important mental action. Psychologists have long introduced this parameter in determining the degree of development of human thinking.
To reinforce the concept of quantity, according to the Montessori program, the children are offered the following exercise:
“Glasses with beans”
There are 10 transparent cups and a bowl with large beans on a tray. Each cup has a number on it. 10 is written on the last cup. The child puts the number of beans into the cup, which is written on the cup. If he does the job right, not a single bean will be left on the tray.
"Mathematical nesting dolls"
In one compartment there are 55 small nesting dolls, and in the other there are smooth square boards with numbers written on them in large print. The child lays out the boards and puts nesting dolls on them, the number should correspond to the written numbers.
The child lays out the boards and puts nesting dolls on them, the number should correspond to the written numbers.
In the younger group, you can do the following exercise:
"Pancakes"
Purpose: to learn to correlate a word with a numeral, a numeral with the quantitative composition of sets.
How to do it.
Using a box with large buttons, the teacher plays "Oladushki" with the children.
Reads the text of the nursery rhyme, distributing it to the children playing on the button, calling the children by name.
Grandmother, grandmother
Baked pancakes.
One - Vanechka,
One - Mashenka, etc.
The buttons are then returned to the box (Pancakes are eaten) and can be counted. In another version of this exercise, the child is given as many buttons as he asks.
Grandmother, grandmother,
Baked pancakes.
Van? (how old is Vanya?)
Misha?
etc.
To work out the ordinal count, you can use an illustration from the work of K. Chukovsky “Cockroach”:
Chukovsky “Cockroach”:
“Bears rode
On a bicycle.
And behind them the cat
Back to front.
And then mosquitoes
On a balloon.
And then crayfish
On a lame dog.
Wolves on a mare.
Lions in a car.
Bunnies in a tram.
A toad on a broom…”
After reading this work, show an illustration.
It is necessary to make sure that the child is well versed in ordinal relations, which in oral speech must be distinguished by intonation.
- How many characters were driving?
- Who rode first?
- Who was fourth?
- Who went after the bunnies, what number?
- Who rode between the crayfish and the lions?
References:
- A.V. Whitish. Formation and development of mathematical abilities of preschoolers.
- V. Volina. Number holiday.
- V.V.Zaitsev. Mathematics for preschoolers.
- HP Metlin. Mathematics in kindergarten.
- E. Hiltunen. I think myself.
Conditions for teaching counting to preschool children
%PDF-1.5 % 10 obj > /Metadata 4 0 R >> endobj 5 0 obj /Title >> endobj 20 obj > endobj 3 0 obj > endobj 40 obj > stream
 32 841.92] /Contents[86 0 R 87 0 R 88 0 R] /group> /Tabs /S /StructParents 0 /Annots [89 0R] >> endobj 70 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 91 0 R /group> /Tabs /S /StructParents 5 >> endobj 80 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 92 0R /group> /Tabs /S /StructParents 8 >> endobj 9 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 93 0 R /group> /Tabs /S /StructParents 9 >> endobj 10 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 94 0 R /group> /Tabs /S /StructParents 10 >> endobj 11 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 96 0R /group> /Tabs /S /StructParents 11 >> endobj 12 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents[86 0 R 87 0 R 88 0 R] /group> /Tabs /S /StructParents 0 /Annots [89 0R] >> endobj 70 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 91 0 R /group> /Tabs /S /StructParents 5 >> endobj 80 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 92 0R /group> /Tabs /S /StructParents 8 >> endobj 9 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 93 0 R /group> /Tabs /S /StructParents 9 >> endobj 10 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 94 0 R /group> /Tabs /S /StructParents 10 >> endobj 11 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 96 0R /group> /Tabs /S /StructParents 11 >> endobj 12 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.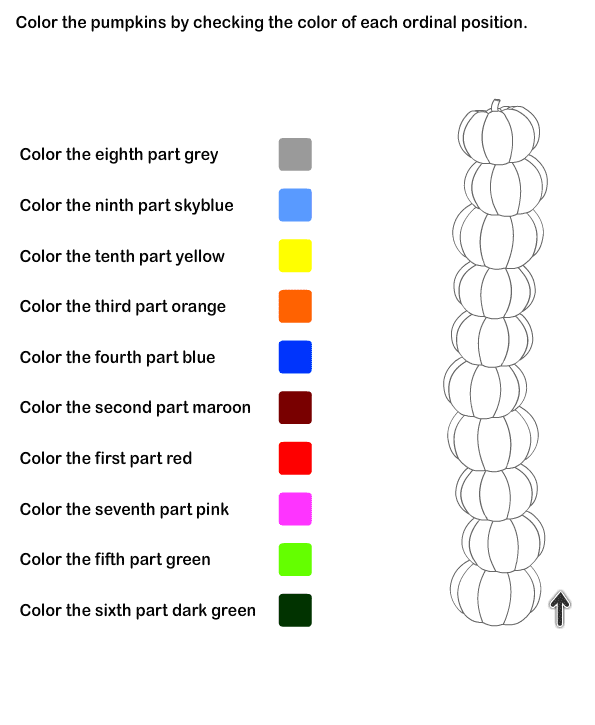 32 841.92] /Contents 97 0 R /group> /Tabs /S /StructParents 12 >> endobj 13 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 98 0 R /group> /Tabs /S /StructParents 13 >> endobj 14 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 99 0R /group> /Tabs /S /StructParents 14 >> endobj 15 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 100 0R /group> /Tabs /S /StructParents 15 >> endobj 16 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 103 0R /group> /Tabs /S /StructParents 16 >> endobj 17 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 104 0 R /group> /Tabs /S /StructParents 17 >> endobj 18 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 105 0 R /group> /Tabs /S /StructParents 18 >> endobj 19 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 97 0 R /group> /Tabs /S /StructParents 12 >> endobj 13 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 98 0 R /group> /Tabs /S /StructParents 13 >> endobj 14 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 99 0R /group> /Tabs /S /StructParents 14 >> endobj 15 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 100 0R /group> /Tabs /S /StructParents 15 >> endobj 16 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 103 0R /group> /Tabs /S /StructParents 16 >> endobj 17 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 104 0 R /group> /Tabs /S /StructParents 17 >> endobj 18 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 105 0 R /group> /Tabs /S /StructParents 18 >> endobj 19 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.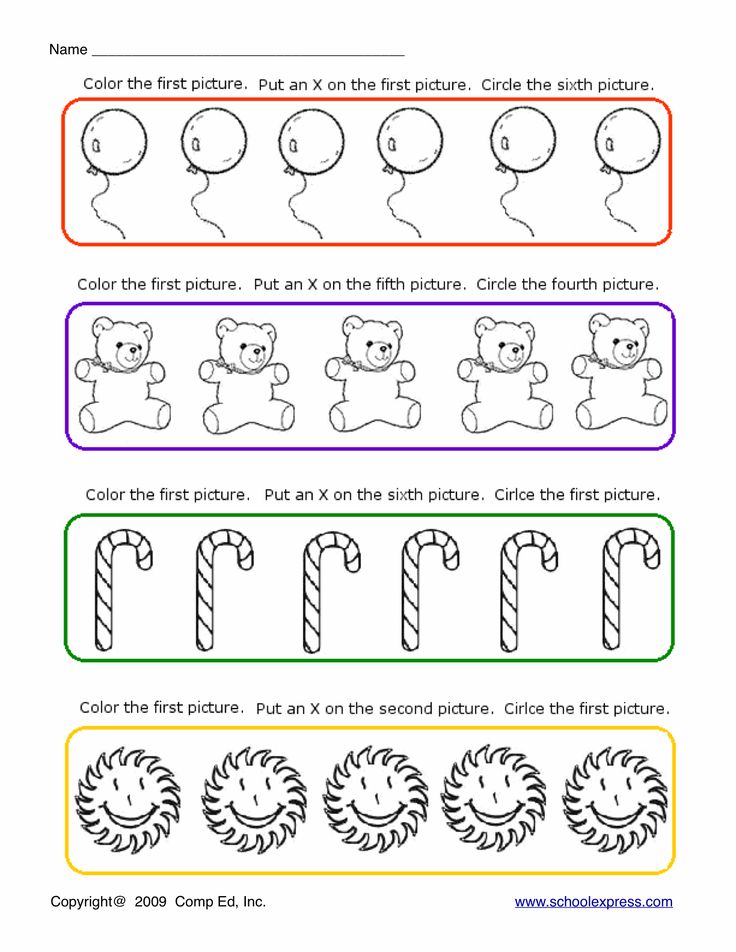 32 841.92] /Contents 106 0 R /group> /Tabs /S /StructParents 19 >> endobj 20 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 107 0 R /group> /Tabs /S /StructParents 20 >> endobj 21 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 108 0R /group> /Tabs /S /StructParents 21 >> endobj 22 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 109 0 R /group> /Tabs /S /StructParents 22 >> endobj 23 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 110 0R /group> /Tabs /S /StructParents 23 >> endobj 24 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 111 0 R /group> /Tabs /S /StructParents 24 >> endobj 25 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 112 0 R /group> /Tabs /S /StructParents 25 >> endobj 26 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 106 0 R /group> /Tabs /S /StructParents 19 >> endobj 20 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 107 0 R /group> /Tabs /S /StructParents 20 >> endobj 21 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 108 0R /group> /Tabs /S /StructParents 21 >> endobj 22 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 109 0 R /group> /Tabs /S /StructParents 22 >> endobj 23 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 110 0R /group> /Tabs /S /StructParents 23 >> endobj 24 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 111 0 R /group> /Tabs /S /StructParents 24 >> endobj 25 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 112 0 R /group> /Tabs /S /StructParents 25 >> endobj 26 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 113 0R /group> /Tabs /S /StructParents 26 >> endobj 27 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 115 0 R /group> /Tabs /S /StructParents 27 >> endobj 28 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 116 0 R /group> /Tabs /S /StructParents 28 >> endobj 29 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 117 0R /group> /Tabs /S /StructParents 29 >> endobj 30 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 118 0 R /group> /Tabs /S /StructParents 30 >> endobj 31 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 119 0 R /group> /Tabs /S /StructParents 31 >> endobj 32 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 120 0R /group> /Tabs /S /StructParents 32 >> endobj 33 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents 113 0R /group> /Tabs /S /StructParents 26 >> endobj 27 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 115 0 R /group> /Tabs /S /StructParents 27 >> endobj 28 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 116 0 R /group> /Tabs /S /StructParents 28 >> endobj 29 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 117 0R /group> /Tabs /S /StructParents 29 >> endobj 30 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 118 0 R /group> /Tabs /S /StructParents 30 >> endobj 31 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 119 0 R /group> /Tabs /S /StructParents 31 >> endobj 32 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 120 0R /group> /Tabs /S /StructParents 32 >> endobj 33 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.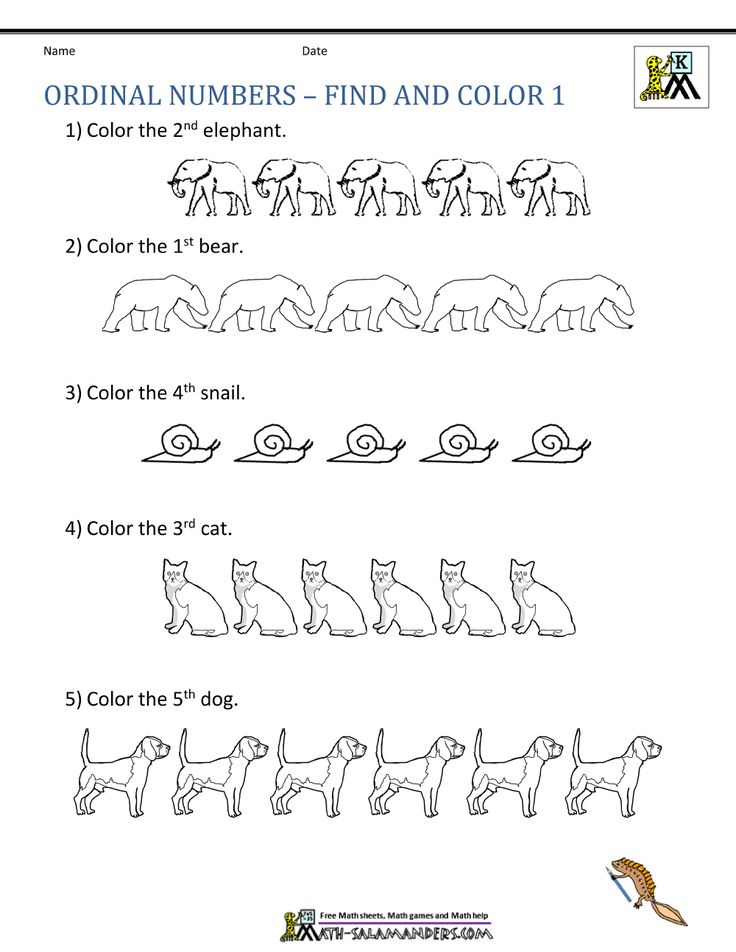 32 841.92] /Contents 121 0 R /group> /Tabs /S /StructParents 33 >> endobj 34 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 122 0 R /group> /Tabs /S /StructParents 34 >> endobj 35 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 123 0 R /group> /Tabs /S /StructParents 35 >> endobj 36 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 124 0R /group> /Tabs /S /StructParents 36 >> endobj 37 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 125 0 R /group> /Tabs /S /StructParents 37 >> endobj 38 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 127 0 R /group> /Tabs /S /StructParents 38 >> endobj 39 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.
32 841.92] /Contents 121 0 R /group> /Tabs /S /StructParents 33 >> endobj 34 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 122 0 R /group> /Tabs /S /StructParents 34 >> endobj 35 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 123 0 R /group> /Tabs /S /StructParents 35 >> endobj 36 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 124 0R /group> /Tabs /S /StructParents 36 >> endobj 37 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 125 0 R /group> /Tabs /S /StructParents 37 >> endobj 38 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 127 0 R /group> /Tabs /S /StructParents 38 >> endobj 39 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.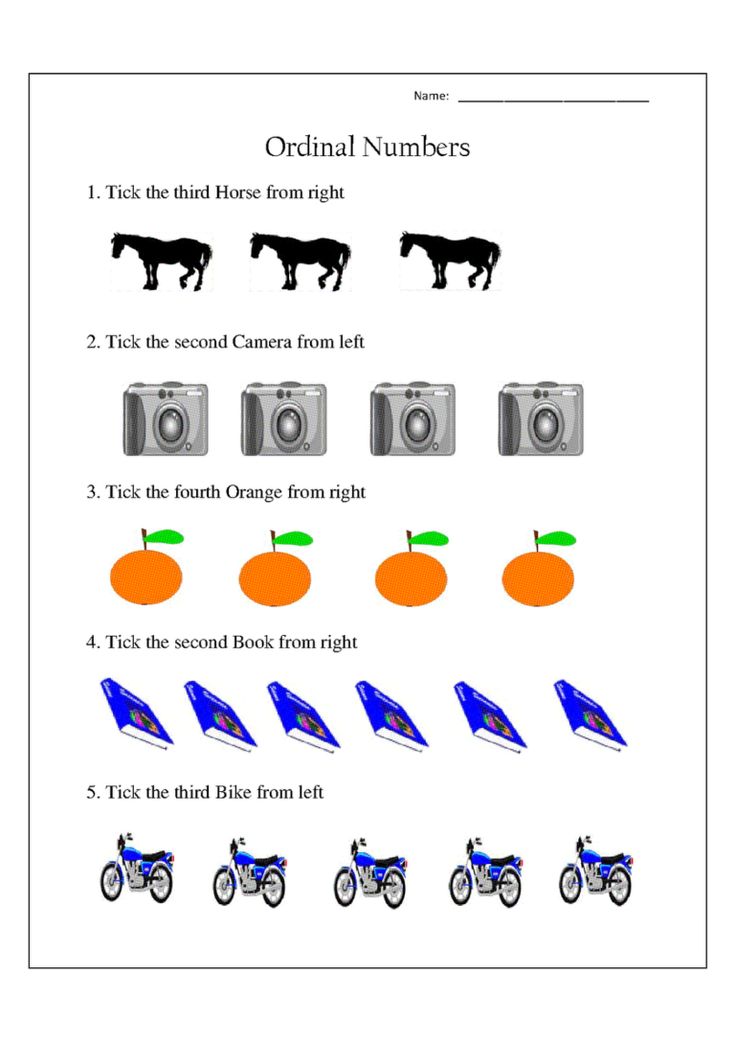 92] /Contents 132 0 R /group> /Tabs /S /StructParents 1 >> endobj 40 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 143 0 R /group> /Tabs /S /StructParents 2 >> endobj 41 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 144 0 R /group> /Tabs /S /StructParents 39 >> endobj 42 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 148 0 R /group> /Tabs /S /StructParents 3 >> endobj 43 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 149 0 R /group> /Tabs /S /StructParents 40 >> endobj 44 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 152 0 R /group> /Tabs /S /StructParents 41 >> endobj 45 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 153 0 R /group> /Tabs /S /StructParents 42 >> endobj 46 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
92] /Contents 132 0 R /group> /Tabs /S /StructParents 1 >> endobj 40 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 143 0 R /group> /Tabs /S /StructParents 2 >> endobj 41 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 144 0 R /group> /Tabs /S /StructParents 39 >> endobj 42 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 148 0 R /group> /Tabs /S /StructParents 3 >> endobj 43 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 149 0 R /group> /Tabs /S /StructParents 40 >> endobj 44 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 152 0 R /group> /Tabs /S /StructParents 41 >> endobj 45 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 153 0 R /group> /Tabs /S /StructParents 42 >> endobj 46 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.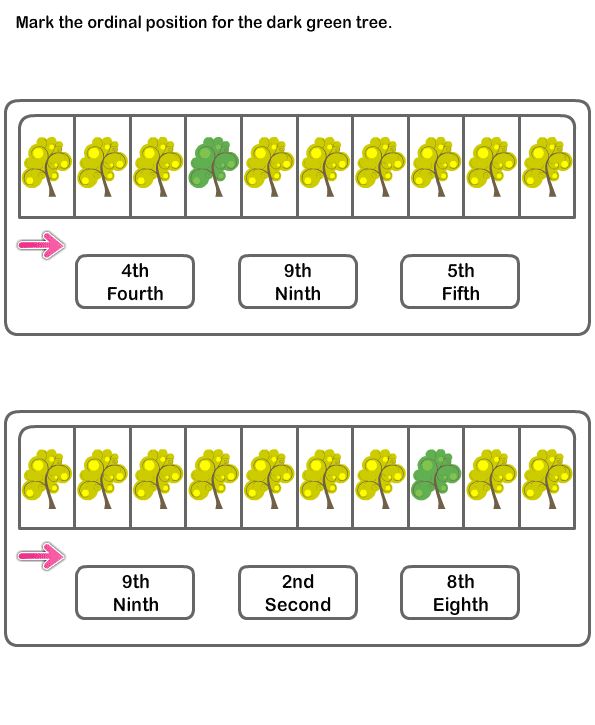 32 841.92] /Contents 154 0 R /group> /Tabs /S /StructParents 43 >> endobj 47 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 155 0R /group> /Tabs /S /StructParents 44 >> endobj 48 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 156 0 R /group> /Tabs /S /StructParents 45 >> endobj 49 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 157 0 R /group> /Tabs /S /StructParents 46 >> endobj 50 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 158 0 R /group> /Tabs /S /StructParents 47 >> endobj 51 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 159 0 R /group> /Tabs /S /StructParents 48 >> endobj 52 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 160 0R /group> /Tabs /S /StructParents 49 >> endobj 53 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 154 0 R /group> /Tabs /S /StructParents 43 >> endobj 47 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 155 0R /group> /Tabs /S /StructParents 44 >> endobj 48 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 156 0 R /group> /Tabs /S /StructParents 45 >> endobj 49 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 157 0 R /group> /Tabs /S /StructParents 46 >> endobj 50 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 158 0 R /group> /Tabs /S /StructParents 47 >> endobj 51 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 159 0 R /group> /Tabs /S /StructParents 48 >> endobj 52 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 160 0R /group> /Tabs /S /StructParents 49 >> endobj 53 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 161 0 R /group> /Tabs /S /StructParents 4 >> endobj 54 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 162 0 R /group> /Tabs /S /StructParents 50 >> endobj 55 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 163 0R /group> /Tabs /S /StructParents 51 >> endobj 56 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 164 0R /group> /Tabs /S /StructParents 52 >> endobj 57 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 165 0 R /group> /Tabs /S /StructParents 53 >> endobj 58 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 166 0 R /group> /Tabs /S /StructParents 54 >> endobj 59 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [167 0R] /MediaBox [0 0 595.
32 841.92] /Contents 161 0 R /group> /Tabs /S /StructParents 4 >> endobj 54 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 162 0 R /group> /Tabs /S /StructParents 50 >> endobj 55 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 163 0R /group> /Tabs /S /StructParents 51 >> endobj 56 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 164 0R /group> /Tabs /S /StructParents 52 >> endobj 57 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 165 0 R /group> /Tabs /S /StructParents 53 >> endobj 58 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 166 0 R /group> /Tabs /S /StructParents 54 >> endobj 59 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [167 0R] /MediaBox [0 0 595. 32 841.92] /Contents 168 0R /group> /Tabs /S /StructParents 55 >> endobj 60 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 169 0 R /group> /Tabs /S /StructParents 57 >> endobj 61 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [170 0 R 171 0 R] /MediaBox [0 0 595.32 841.92] /Contents 172 0 R /group> /Tabs /S /StructParents 58 >> endobj 62 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [173 0 R 174 0 R 175 0 R] /MediaBox [0 0 595.32 841.92] /Contents 176 0R /group> /Tabs /S /StructParents 61 >> endobj 63 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 177 0 R /group> /Tabs /S /StructParents 65 >> endobj 64 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 178 0 R /group> /Tabs /S /StructParents 66 >> endobj 65 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 168 0R /group> /Tabs /S /StructParents 55 >> endobj 60 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 169 0 R /group> /Tabs /S /StructParents 57 >> endobj 61 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [170 0 R 171 0 R] /MediaBox [0 0 595.32 841.92] /Contents 172 0 R /group> /Tabs /S /StructParents 58 >> endobj 62 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [173 0 R 174 0 R 175 0 R] /MediaBox [0 0 595.32 841.92] /Contents 176 0R /group> /Tabs /S /StructParents 61 >> endobj 63 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 177 0 R /group> /Tabs /S /StructParents 65 >> endobj 64 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 178 0 R /group> /Tabs /S /StructParents 66 >> endobj 65 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 179 0 R /group> /Tabs /S /StructParents 67 >> endobj 66 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 180 0 R /group> /Tabs /S /StructParents 68 >> endobj 67 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 181 0 R /group> /Tabs /S /StructParents 69 >> endobj 68 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 182 0 R /group> /Tabs /S /StructParents 70 >> endobj 69 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 183 0 R /group> /Tabs /S /StructParents 71 >> endobj 70 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 184 0 R /group> /Tabs /S /StructParents 72 >> endobj 71 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 186 0 R /group> /Tabs /S /StructParents 73 >> endobj 72 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents 179 0 R /group> /Tabs /S /StructParents 67 >> endobj 66 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 180 0 R /group> /Tabs /S /StructParents 68 >> endobj 67 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 181 0 R /group> /Tabs /S /StructParents 69 >> endobj 68 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 182 0 R /group> /Tabs /S /StructParents 70 >> endobj 69 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 183 0 R /group> /Tabs /S /StructParents 71 >> endobj 70 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 184 0 R /group> /Tabs /S /StructParents 72 >> endobj 71 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 186 0 R /group> /Tabs /S /StructParents 73 >> endobj 72 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.