Ordinal numbers maths

What are Ordinal Numbers? Definition, List, Examples, Facts

What are Ordinal Numbers?

Numbers that are used to represent the rank or position of an object or a person are known as ordinal numbers. They are also referred to as positioning or ranking numbers.The sequence of ordinal numbers vary on the parameters that are based on the positions that are defined, such as weight, height, marks, size, etc. Such numbers are also known as ordinals.

How to Write Ordinal Numbers?

Ordinal numbers or ordinals are written using numerals as prefixes and adjectives as suffixes.

For example, 1st, 2nd, 3rd, 4th, 5th, 6th, 7th, 8th and so on. We can easily identify an ordinal number: it talks about positioning.

So, if we were to say, “Bring me the bottle of jam that is lying on the 4th shelf.”, one would know that the ordinal number here is 4, which informs us about the position of the jam bottle.

The above picture shows different floors of a building. Here, we can use ordinal numbers to define the position of the floors.

The numbers 1st (first), 2nd (second), 3rd (third), 4th (fourth), 5th (fifth), 6th (sixth), 7th (seventh), 8th (eighth), 9th (ninth) and 10th (tenth) tell us about the positions of various floors in the building. Therefore, all of them are the ordinal numbers.

Applications of Ordinal Numbers

Ordinal numbers are a great way to talk about the order of something. For example, the order of dates. These numbers are only used when data is provided and the data is to be arranged in order.

For example: Someone who has performed well throughout the year may get the chance to be valedictorian. They would be first in line. But someone who performed well, but was unable to score as much as the person before in various tests and exams, may be second in line to be valedictorian. The person who has not performed well at all, has the least amount of chance.

The picture given below shows some athletes competing in a 500-m race. We can also use ordinal numbers to define their positions in order to see who the winner and runners-up of the race are.

Other examples of ordinal numbers are as follows:

Jennifer always ranks 2nd in the class.

Here 2nd is the ordinal number that tells you about the position that Jennifer has secured.

Jane is standing at the 5th place in the queue.

Hereby the ordinal number is 5th, we understand Jane’s position in the queue.

Jenny came 3rd in the race.

Here, 3rd is the ordinal number which tells you about the place that Jenny has secured in the race.

The 10th table is reserved.

Here, the ordinal number 10th refers to the number of table reservations made.

Ordinal Numbers 1

– 50 list

Ordinal Numbers 51

–100 list

Ordinal Numbers v. Cardinal Numbers

The type of numbers that are used for counting the number of objects or persons are known as cardinal numbers. This type of numbers are used for representing the cardinality of the number of elements in a set.

Cardinality means to know about the number of elements in a set.

Cardinal numbers can be the natural numbers that we use while we are counting like one, two, three, four, five and so on.

On the other hand, ordinal numbers are used to determine the rank or position of any object or person. We write ordinal numbers using numbers as prefixes and adjectives as suffixes.

Let us understand the difference with the help of an example.

Some students were asked to collect marbles.

Tom collected 1, Jane collected 2, and Clove collected 3 marbles.

Here the numbers 1, 2, 3 are cardinal numbers as they represent the quantity of marbles.

Now, the one who scores maximum wins. So, Clove stands 1st, Jane stands 2nd and Tom stands 3rd.

Here the numbers 1st, 2nd and 3rd are ordinal numbers as they represent the position of the students.

Ordinal Numbers v. Nominal Numbers

A set of numbers that are used for labeling certain items or places so that they can be identified easily are known as nominal numbers. Whenever we have to identify an object uniquely, we use nominal numbers. These numbers are not of much use because they are just going to give information about location and not about its quantity, quality, etc. Nominal numbers can be used as area codes, on number plates of vehicles, etc. Operations such as addition, subtraction, multiplication and division are meaningless on nominal numbers.

For example: In a phone number like 202 588-6500, the number is a nominal number. Even if we apply an operation, it will not give us anything meaningful.

On the order hand, the ordinal numbers tell us about the rank or position of any object or person.

For example: Sophia lives in the 34th house on San Pablo Avenue, California.

Fun Fact!

11, 12 and 13 are the only numbers to use a suffix ‘–th’ but all other numbers ending with 1 use ‘–st’, those ending with 2 use ‘–nd’ and those ending with 3 use ‘–rd’.

Solved Examples

Example 1: Which English alphabet is 12th from the beginning?

Solution: The alphabet that is 12th from the beginning is L.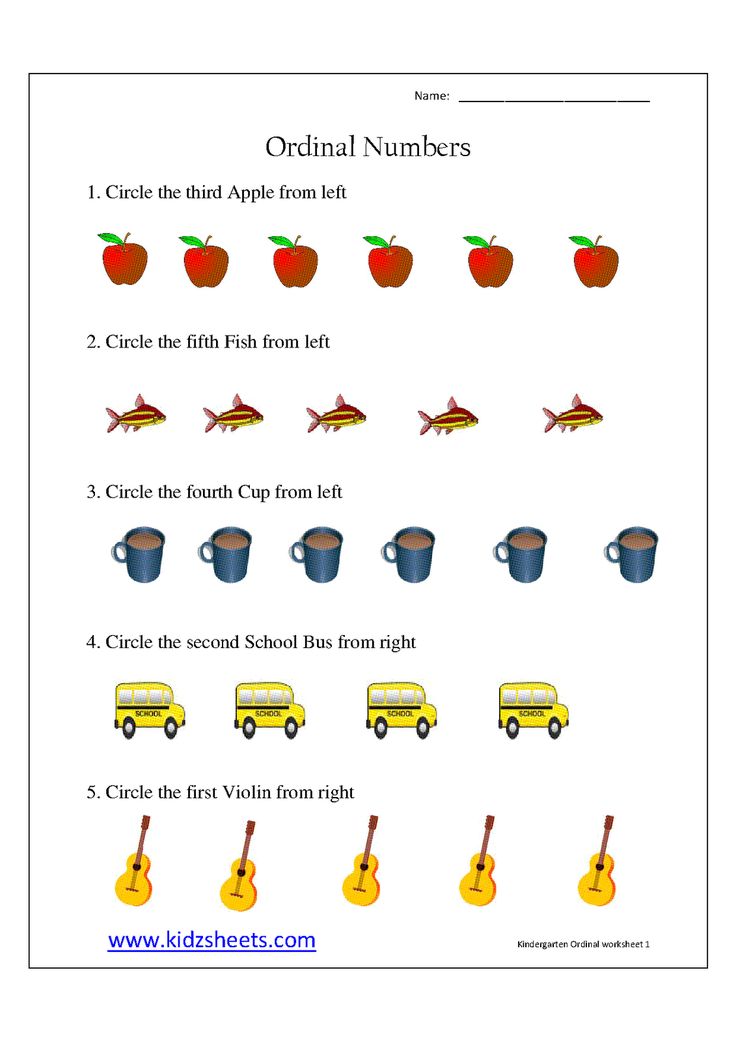

Example 2: Kim, Kethy, Kiah and Kaina are sitting in the line in alphabetical order. What is the position of Kiah from the beginning?

Solution: According to alphabetical order, the order in which they’re sitting would be: Kaina, Kethy, Kiah, Kim. So, Kiah is at the 3rd position.

3. Christmas lies on the _____ of December. Solution: Christmas lies on the 25th of December.

Practice Problems

The vehicle number of Sarah is KL23AB89.

There are 9 apples on the tree.

Catheline came 4th in the drawing competition.

None of these

Correct answer is: Catheline came 4th in the drawing competition.
In the option C, the number 4th is telling about the position of Catheline in the drawing competition.

51st

51th

51rd

Correct answer is: 51st
The ordinal number for 51 for 51st.

M and O

M and N

P and I

E and O

Correct answer is: P and I
The fourth letter is P and the tenth letter is I.

Frequently Asked Questions

Is 0 an ordinal number?

No, we cannot write 0 as an ordinal number.

What are exceptional ordinal numbers?

Exceptional ordinal numbers are the ordinal numbers that do not end with -th. For example: 1st (first), 2nd (second), 3rd (third), etc.

Who invented ordinal numbers?

Ordinal numbers were invented by Georg Cantor in 1883.

Ordinal Numbers - Meaning, Examples

Ordinal numbers are the numbers that talk about the position of objects. For example, 'The cookies are kept in the 3^rd drawer from the top', 'The orange dress is the 7^th one from the right', 'The soccer ball is kept in the 3^rd carton from the left'. All these sentences have one thing in common - they talk about the positions of the objects. This is the main element in the discussion of ordinal numbers.

1.	What are Ordinal Numbers?
2.	Difference Between Cardinal and Ordinal Numbers
3.	List of Ordinal Numbers from 1 to 100
4.	FAQs on Ordinal Numbers

What are Ordinal Numbers?

An ordinal number is a number that indicates the position or order of something in relation to other numbers, like, first, second, third, and so on. This order or sequence may be according to the size, importance, or any chronology. Let us understand the ordinal numbers with an example. Ten students participated in a contest. Out of them, the top winners were given medals and were ranked as 1^st, 2^nd, and 3^rd. In this case, the positions: 1^st, 2^nd, and 3^rd are ordinal numbers.

Difference Between Cardinal and Ordinal Numbers

A cardinal number is a number that denotes the count of any object. Any natural number such as 1, 2, 3, etc., is referred to as a cardinal number, whereas, an ordinal number is a number that denotes the position or place of an object. For example, 1^st, 2^nd, 3^rd, 4^th, 5^th, etc. Now, if we say, 'There are 3 ants and 5 bears'. This is an example of cardinal numbers. However, if we say, 'The position of the runners in the running event is first, second, third, and so on', this represents ordinal numbers. Observe the table given below to note the difference between cardinal numbers and ordinal numbers.

List of Ordinal Numbers from 1 to 100

The list of ordinal numbers from 1 to 100 can be learned easily and is quite helpful for specifying the order of any given object. You can use the combinations from this list to find out the ordinal numbers from 100 onward. Observe the table given below in order to understand how ordinal numbers are written. You might be able to pick up a pattern after referring to the first twenty ordinal numbers.

1st: First	21st: Twenty-First	41st: Forty-First	61th: Sixty-First	81st: Eighty-First
2nd: Second	22nd: Twenty-Second	42nd: Forty-Second	62nd: Sixty-Second	82nd: Eighty-Second
3rd: Third	23rd: Twenty-Third	43rd: Forty-Third	63rd: Sixty-Third	83rd: Eighty-Third
4th: Fourth	24th: Twenty-Fourth	44th: Forty-Fourth	64th: Sixty-Fourth	84th: Eighty-Fourth
5th: Fifth	25th: Twenty-Fifth	45th: Forty-Fifth	65th: Sixty-Fifth	85th: Eighty-Fifth
6th: Sixth	26th: Twenty-Sixth	46th: Forty-Sixth	66th: Sixty-Sixth	86th: Eighty-Sixth
7th: Seventh	27th: Twenty-Seventh	47th: Forty-Seventh	67th: Sixty-Seventh	87th: Eighty-Seventh
8th: Eighth	28th: Twenty-Eighth	48th: Forty-Eighth	68th: Sixty-Eighth	88th: Eighty-Eighth
9th: Ninth	29th: Twenty-Ninth	49th: Forty-Ninth	69th: Sixty-Ninth	89th: Eighty-Ninth
10th: Tenth	30th: Thirtieth	50th: Fiftieth	70th: Seventieth	90th: Ninetieth
11th: Eleventh	31st: Thirty-First	51st: Fifty-First	71st: Seventy-First	91st: Ninety-First
12th: Twelfth	32nd: Thirty-Second	52nd: Fifty-Second	72nd: Seventy-Second	92nd: Ninety-Second
13th: Thirteenth	33rd: Thirty-Third	53rd: Fifty-Third	73rd: Seventy-Third	93rd: Ninety-Third
14th: Fourteenth	34th: Thirty-Fourth	54th: Fifty-Fourth	74th: Seventy-Fourth	94th: Ninety-Fourth
15th: Fifteenth	35th: Thirty-Fifth	55th: Fifty-Fifth	75th: Seventy-Fifth	95th: Ninety-Fifth
16th: Sixteenth	36th: Thirty-Sixth	56th: Fifty-Sixth	76th: Seventy-Sixth	96th: Ninety-Sixth
17th: Seventeenth	37th: Thirty-Seventh	57th: Fifty-Seventh	77th: Seventy-Seventh	97th: Ninety-Seventh
18th: Eighteenth	38th: Thirty-Eighth	58th: Fifty-Eighth	78th: Seventy-Eighth	98th: Ninety-Eighth
19th: Nineteenth	39th: Thirty-Ninth	59th: Fifty-Ninth	79th: Seventy-Ninth	99th: Ninety-Ninth
20th: Twentieth	40th: Fortieth	60th: Sixtieth	80th: Eightieth	100th: Hundredth

Ordinal Numbers 1 to 20

Ordinal numbers from 1 to 20 are different from the rest. After the number 20, a repeated pattern of ordinal numbers can be observed. Ordinal numbers from 1 to 20 can be listed as follows. 1 - First, 2 - Second, 3 - Third, 4 - Fourth, 5 - Fifth, 6 - Sixth, 7 - Seventh, 8 - Eighth, 9 - Ninth, 10 - Tenth, 11 - Eleventh, 12 - Twelfth, 13 - Thirteenth, 14 - Fourteenth, 15 - Fifteenth, 16 - Sixteenth, 17 - Seventeenth, 18 - Eighteenth, 19 - Nineteenth, 20 - Twentieth.

☛ Related Topics

Cardinal Numbers
Ordinal Numbers Worksheets for Kindergarten
Numbers
Rational Numbers
Prime Numbers
Composite Numbers
Even Numbers
Odd Numbers
Real Numbers
Natural Numbers
Irrational Numbers
Counting Numbers

Ordinal Numbers Examples

Example 1: What is the 3rd letter in the word: SUMMERS?
Solution:
In the given word, SUMMERS, the first letter is 'S'. The second letter is 'U'. Similarly, we count the position of the letters in order, like, first, second, third, and so on which denotes ordinal numbers. So, we can see that the letter 'M' comes in the 3rd position. Therefore, the third letter in the given word is 'M'.
Example 2: Sam, Jenny, Mary, and Jack are standing in a queue in the given order. Who is in the fourth position?
Solution:
From the given information, we can say that: Sam is in the first place, Jenny is in the second place, Mary is in the third place, and Jack is in the fourth place. Therefore, Jack is standing in the fourth position. Here, 4th is an ordinal number because it denotes the position of Jack.
Example 3: State true or false with respect to ordinal numbers.
a.) An ordinal number is a number that denotes the position or place of an object.
b.) Ordinal numbers are written as 1^st, 2^nd, and 3^rd, and so on.
Solution:
a.) True, an ordinal number is a number that denotes the position or place of an object.
b.) True, ordinal numbers are written as 1^st, 2^nd, and 3^rd, and so on.

go to slidego to slidego to slide

Ready to see the world through math’s eyes?

Math is a life skill. Help your child perfect it through real-world application.

Book a Free Trial Class

Practice Questions on Ordinal Numbers

go to slidego to slide

FAQs on Ordinal Numbers

What Does Ordinal Number mean?

Ordinal numbers are the numbers that specify the position of objects. For example, when we say that the books are kept on the 3^rd shelf, here 3rd is an ordinal number. Similarly, first, second, twentieth, fiftieth, and so on are ordinal numbers.

What is the Difference Between Cardinal and Ordinal Numbers?

Cardinal numbers denote the count of any object. For example, natural numbers like 1, 2 3, and so on are cardinal numbers. On the other hand, ordinal numbers denote the position or place of an object. For example, 1^st, 2^nd, 3^rd, 4^th, 5^th, and so on, are ordinal numbers.

How to Write Dates with Ordinal Numbers?

Ordinal numbers are used to mention the dates in English. For example, if we need to write the date of Christmas, we write the month and then the ordinal number of the day. In this case, we say that Christmas is on December 25th. Here, 25th is an ordinal number.

Is Zero an Ordinal Number?

No, 0 cannot be considered an ordinal number. Specifying the position of anything as 0^th or zeroth does not give a logical explanation.

How to Write Ordinal Numbers?

Ordinal numbers have a suffix added at the end. They can be written as first, second, third, and so on when expressed in words. When ordinal numbers are expressed as numerals, the last two letters of the words are added to the respective numbers, like, 1^st, 2^nd, 3^rd, 4^th, and so on.

Why do we use Ordinal Numbers?

We use ordinal numbers for specifying the position or order of something. For example, the pens are kept in the 3^rd drawer from the top, or, Ria stays on the second floor of the apartment. Here, the respective numbers specify the position or order of the object or people, whatever the case may be.

What are Ordinal Numbers From 1 to 10?

The ordinal numbers from 1 to 10 are as follows: 1st: First, 2nd: Second, 3rd: Third, 4th: Fourth, 5th: Fifth, 6th: Sixth, 7th: Seventh, 8th: Eighth, 9th: Ninth, and 10th: Tenth.

What is the Ordinal Number of 1?

The ordinal of 1 is written as First. In the numeral form, it is represented as 1^st.

Download FREE Study Materials

Worksheets on Ordinal Numbers

Item count. Cardinal and ordinal numbers.

Lesson 1. Subject "Mathematics". Item count. Cardinal and ordinal numbers.

Objectives: To introduce the subject, the "Mathematics" set; identify the ability to count objects; find out at what level ordinal representations are formed, teach how to correctly name ordinal numbers; create conditions for the development of observation, attention.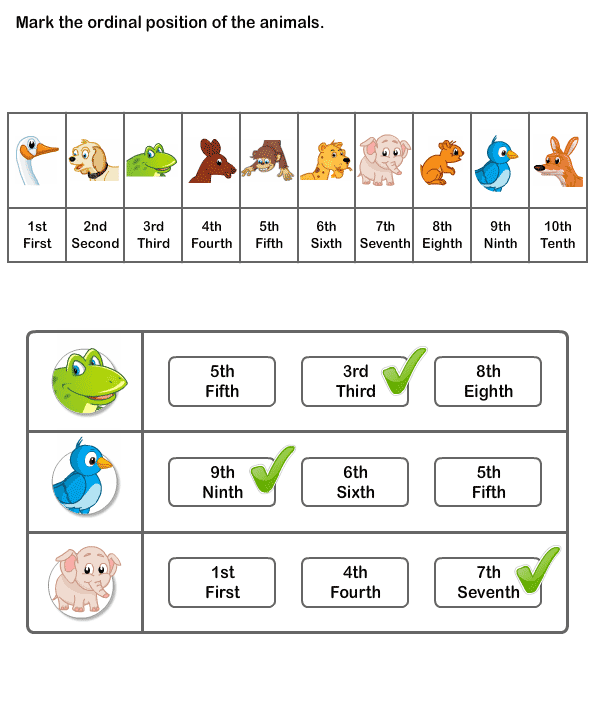

Planned results: The student knows: what the science of "Mathematics" studies; knows how to: navigate the textbook and printed notebook; find in the textbook and explain the symbols of the textbook, count items up to 10; classify objects according to their characteristics; compare objects and highlight common or distinctive features; name the numbers in the order in which they appear when counting; count a given number of items from a set of items (8-10 individual items)

Organizational moment.

Teacher : Hello guys.

The long-awaited call is given,

The lesson begins.

Teacher : What should you do when you hear the bell? (Stand beside your seat.)

I'm glad to meet you. Thank you for coming. Who remembers my name? Well done, you have a great memory.

Teacher: To be honest, I don't remember all of you. I don't think you remember all of them. We will have plenty of time to get to know each other better.

Teacher: Please check if you are ready for the lesson. We should have on our desk: a textbook, a notebook, a pencil case with pencils and felt-tip pens.

Teacher: Who remembers how many children there are in our class? And how many boys? Girls? (praise those who raise their hand).

Teacher: What is the raised hand for? A raised hand is needed so that I understand who is ready to answer the question.

Getting to know the subject and the Mathematics curriculum.

Teacher: Guys, today is an unusual day for you - you came to the first math lesson in your life. I congratulate you on this event and want to wish that the study of mathematics is interesting for you. Let's read the name of the subject (On the board: MA-TE-MA-TI-KA)

Teacher: What do you think we will do in mathematics lessons? (Count, solve examples, problems ...).

Teacher: The science of mathematics is one of the oldest. People need it to transform the world around them. You will learn how to count, measure, solve problems. (Knowledge of mathematics is necessary both in everyday life and in work.)

Teacher: In mastering mathematics, a textbook consisting of two books will help us. It was written by M. I. Moro, S. I. Volkova and S. V. Stepanova. You will need two notebooks in which you can draw, color, write, but only in specially designated places.

Teacher: Let's look at our textbook, how beautiful and interesting it is. Consider the flyleaf - the cover of the textbook. Tell us who and what is depicted there? You and I, just like this boy, will climb the steps of knowledge higher and higher.

Teacher: The first task is to wrap the textbook, sign it, and be sure to make bookmarks.

Teacher: Turn the page. On the page on the left, you see helper icons that will tell you how to complete the task correctly. (Pay attention to their decoding).

Teacher: Why did the authors of the textbook come up with symbols for tasks, and do not write them in words? (Reading tasks for a long time, and looking at the legend, you can immediately understand what to do. )

Teacher: And on the right side of the page is the first topic we will study. (Children read the title of the topic).

Teacher: So where do we start studying mathematics? From the item count.

Exercise in counting objects.

Teacher: Who among you already knows how to count? Shall we check now?

Teacher: Then let's count in chorus to 10. (Students count in chorus under the guidance of the teacher). Well done! You know how to count.

Teacher: Now look who came to visit us. (There are 5 fairy-tale heroes on the board). Preparation of heroes.

Teacher : Let's count in chorus how many guests we have. Well done! Raise your hand those who can continue the count further? Excellent!

Teacher: Tell me which of the guests is on the left? On right? in the middle?

Teacher: Attention difficult question: Who is second from the left? Tell me how did you know? Who is second from the right? First on the left? First on the left? Third from the right?

Teacher : I need five helpers.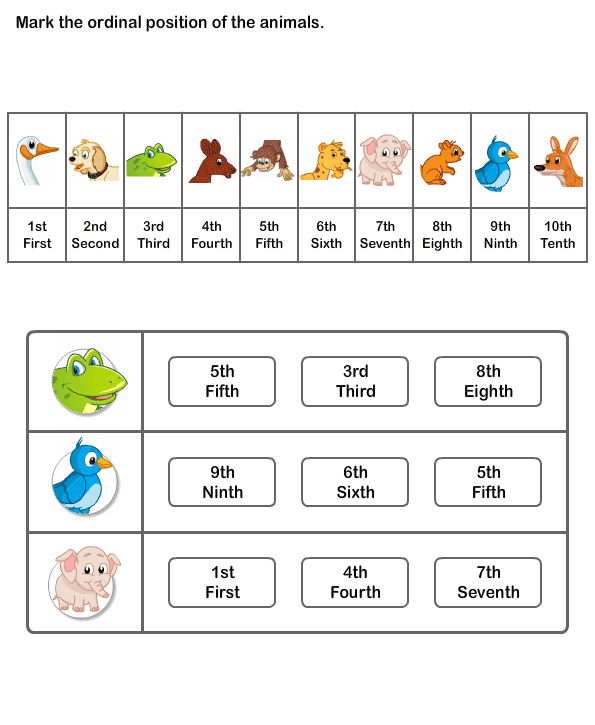

The teacher calls five volunteers to the board and lines them up.

Teacher : Do you remember the fairy tale about the kid who counted everyone? How did he do it? Let's count our assistants in the same way. Lena - one, Seryozha - two...

Name the first from the left, the second from the right, the third from the left, the fifth from the right.

It is important , that all children be named .

Work using visual material and textbook (p. 4, part 1)

Teacher : And now open the textbook on page 4. Look at the lesson in the forest school? What number did teacher Filin ask to show?

Teacher : How many bunnies do you see? How many cubs? How many whites?

Now you try to be teachers: instead of me, ask the class questions about the picture, starting with the word “how much”.

Listen to the rhyme that the animals have learned.

The teacher reads the rhyme on page 4 and invites the children to show it with movements.

Children ask each other questions with the word "how much".

How many yellow apples?
How many big ones?
How many little ones?
How many carrots do rabbits have?
How many mushrooms do squirrels have?
How many daisies?

How many bells?

Physical education minute

One - rise, stretch,

Two - bend down, straighten,

Three - three claps in the hands,

Three nods with the head.

Four - arms wider,

Five - wave arms,

Six - sit quietly in place.

1. Preparation for the perception of ordinal numbers.

Teacher : Listen to the riddle:

Seryozhka fell into the snow, followed by Alyoshka,

And Irinka followed him, and Marinka followed,

And then Ignat fell.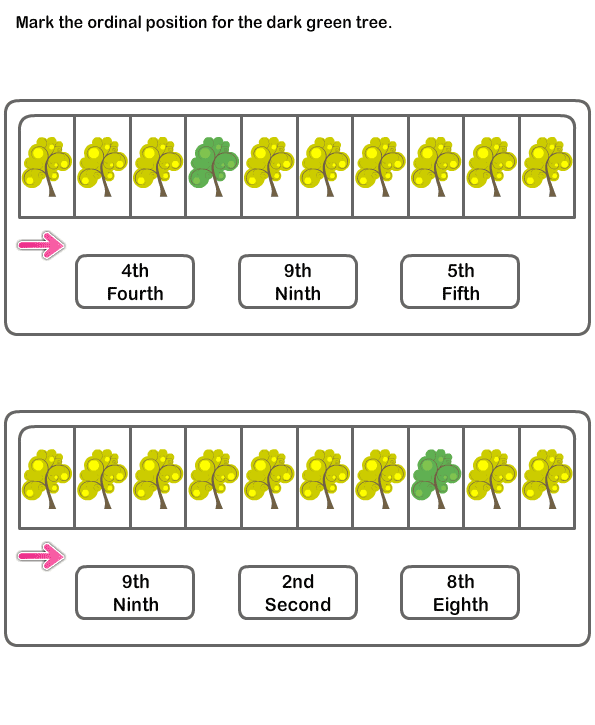 How many guys are in the snow?

Teacher : Who fell into the snow first? Who is behind him?

Teacher : Who was the last one on the snow?

Teacher : Let's count the guys in the order in which they fell into the snow.

They count as a choir under the guidance of a teacher:

First - Seryozhka, second - Alyoshka, third - Irinka, fourth - Marinka, fifth - Ignat.

Ignat.

2. Formation of the ability to count objects in order.

Reads an excerpt from K. I. Chukovsky's poem "Cockroach":

Bears were riding a bicycle.

And behind them is the cat backwards.

And then there are mosquitoes on a balloon.

And behind them are crayfish on a lame dog.

Wolves on a mare,

Lions in a car, bunnies in a tram, toad on a broom . ..

Bunnies in a tram,

Toads on a broom ...

9000 Now let's count how many children sit in our class in each row? (Count in chorus).

Count all the animals in order. Now count them in reverse order: from right to left.

(Bear, cat, mosquito, cancer, wolf, lion, bunny, toad. They count in a chorus in forward and reverse order under the guidance of a teacher.) You can put pictures of animals on the board. (Preparation of characters).

Teacher : Open the textbook on p.5. Work according to the textbook (p. 5).

- What is shown in the picture?

What color engine is the train carrying?

Who is in the first carriage? Who is in the second?

How many wagons does the train pull in total?

Let's count all the passengers in order.

Will anything change if the train is driven by a green engine?

Which trailer will be the first?

Who rides in it? Who will follow him?

And who will be in the last carriage?

Now let's count all the passengers in order. (Look at the picture in the textbook and answer the teacher's questions).

Teacher : Now let's count the items in order. (Hangs up a plot picture on the board and asks the students to count various objects on it in order). Prepare visual material of animals, birds…)

Physical education for the eyes.

Children stay at their desks .

Eyes need to rest. (Guys close their eyes )
Take a deep breath. (Deep breath. Eyes still closed)
Eyes running around. (Eyes open. Pupil movement in a circle clockwise and counterclockwise)
Blink many, many times (Frequent blinking of the eyes)
Eyes feel good . (Lightly touching closed eyes with fingertips)
Open eyes, we continue the lesson ! ( Eyes wide open. There is a wide smile on his face.)

Teacher : Guys, Dunno was asked to find all the circles among these figures. He did this work like this... (The teacher leaves all the red pieces, and removes the rest, but so that the children can see the pieces removed from the board.)

Teacher : Did Dunno complete the task correctly? (Not).

Why do you think so?

On what basis did he unite the figures? (By color).

How was the task to be completed? Help the Unknown.

Name the figures that you removed. (They remove the square, the triangle and put a yellow circle on the board.) Perform a mutual check.

Working with geometric material.

On the board: geometric figures (see textbook, p. 5), Dunno figurine. (Make a printout).

Teacher : Draw a square, a circle, a triangle in your notebooks.

Check each other's work.

(They remove the square, the triangle and put a yellow circle on the board.) Perform a mutual check.

Summing up.

Teacher : Guys, let's close the textbook and think about what we did in the lesson? (Counted.)

Do you remember what goal we set at the beginning of the lesson? Have we achieved this goal?

What question was answered? (How many? Where?)

What figures did we consider in the textbook?

Which task did you like the most? Why? What more work would hotels do?

Teacher : Hold up the mood cards and rate the lesson. Thanks to all. The lesson is over.

9000 9000 9000

CROPROWN OF CROPROWN Set theory ....

Hello, you will learn about the ordinal number Let's analyze its main types and features of use. There will be many more detailed examples and descriptions. In order to better understand what is ordinal number , I highly recommend reading everything from the Discrete Mathematics category. Set Theory. Graph Theory. Combinatorics..

Image of ordinal numbers from 0 to . Each turn of the spiral corresponds to one power

In set theory ordinal , or ordinal (Latin ordinalis - ordinal) is the ordinal type of a completely ordered set. As a rule, ordinal numbers are identified with hereditarily transitive sets. Ordinals are one of the extensions of natural numbers, different from both integers and cardinal numbers. Like other kinds of numbers, they can be added, multiplied, and raised to a power. Infinite ordinal numbers are called transfinite (lat. trans - for, through + finitio - edge, limit). Ordinals play a key role in proving many theorems of set theory, in particular due to the principle of transfinite induction associated with them.

Ordinal numbers were introduced by Georg Cantor in 1883 as a way to describe infinite sequences and to classify sets that have a certain ordered structure. ^{He accidentally discovered ordinal numbers while working on a problem involving trigonometric series.}

Sets and have the same cardinality if it is possible to establish a bijective correspondence between them (that is, specify a function that is simultaneously injective and surjective: each of corresponds to the only one of , and each of is the image of the only one of ).

Suppose that the sets and are given partial orders and, respectively. Then partially ordered sets and are said to be order-preserving isomorphic if there exists a bijective map such that the given order is preserved. In other words, if and only if . Any a well-ordered set is order-preserving isomorphic with respect to a naturally ordered set of ordinal numbers less than some definite ordinal (equal to the ordinal type ).

Finite ordinal (and cardinal) numbers are numbers of the natural series: 0, 1, 2, …, since any two complete orderings of a finite set are isomorphic with order conservation. The smallest infinitely large the ordinal number is identified with the cardinal number. However, in the case of transfinite numbers greater than , ordinals—compared to cardinal numbers—allow us to express a finer classification of sets based on information about their ordering. While all countable sets are described by one cardinal number equal to , the number of countable ordinals is infinitely large and, moreover, uncountable:

In this case, addition and multiplication do not have the property of commutativity: thus, it coincides with but differs from ; similar but not the same. The set of all countable ordinals forms the first uncountable ordinal number corresponding to the cardinal number (next number after ). Well-ordered cardinal numbers are identified with their initial ordinals, that is, the minimal ordinals of the corresponding cardinality. The cardinality of the ordinal number specifies a many-to-one correspondence between the classes of ordinal and cardinal numbers.

Usually an arbitrary ordinal is defined as the ordinal type of the set of ordinals strictly less than . This property allows us to represent any ordinal number as a set of ordinals strictly less than itself. All ordinal numbers can be divided into three categories: zero, the next ordinal, and the limiting ordinal (the latter differ in their confinality). For a given class of ordinal numbers , you can specify its th element - in other words, the elements of the class can be indexed (counted). Such a class will be closed and unbounded provided that the indexing function is continuous and never stops. Cantor's normal form allows any ordinal number to be uniquely represented as a finite sum of ordinal powers. However, this form cannot be used as a basis for a universal ordinal notation system due to the presence of self-referential representations in it: for example, . You can define ever larger ordinal numbers, but as they grow, their description becomes more complicated. Any ordinal number can be represented as a topological space by assigning an ordinal topology to it. Such a topology will be discrete if and only if the corresponding ordinal does not exceed a countable cardinal number, that is, is less than or equal to . A subset will be open in the order topology if and only if it is cofinite or does not contain as an element.

Ordinal numbers as an extension of the set of natural numbers

Natural numbers (which in this case also includes 0) have two main applications: the description of the size of a certain set and the description of the position of an element in a given sequence. In the case of finite sets, these concepts coincide; up to isomorphism, there is only one way to arrange the elements of a finite set as a sequence. In the case of infinite sets, it is necessary to distinguish the concept of size and the cardinal numbers associated with it from the concept of position, the generalization of which is the ordinal numbers described in this article. This is explained by the fact that an infinite set, having a uniquely defined size (cardinality), can be well ordered in more than one non-isomorphic way.

While the concept of a cardinal number associated with a set does not require any structure to be specified on it, ordinals are closely related to a special kind of set called well-ordered (in fact, these concepts are so close that some mathematicians do not they make no difference). This term refers to a linearly ordered set (that is, a set with some uniform way of choosing the smallest and largest value for an arbitrary pair of elements) in which there is no infinite decreasing sequences (although there may be infinitely increasing ones), or - in an equivalent formulation - a set in which any non-empty subset contains the smallest element. Ordinal numbers can be used both to denote the elements of any given well-ordered set (the smallest element is labeled 0, the next one is labeled 1, the next one is 2, "and so on"), and to measure the "size" of the entire set by specifying the smallest ordinal that is not the label of any element of the set. This "size" is called ordinal type set.

Any ordinal number is defined by the set of preceding ordinals: in fact, the most common definition of the ordinal number identifies with the set of preceding ordinals. Thus, the ordinal 42 is the ordinal type of the set of preceding ordinals, that is, the ordinals from 0 (the smallest ordinal) to 41 (the immediate predecessor of 42), and is usually identified with the set . The converse is also true: any downward-closed set of ordinals—that is, such that, for any ordinal and any ordinal, the ordinal is also an element—is itself an ordinal (or can be identified with one).

Up to this point, we have only mentioned finite ordinals that coincide with natural numbers. In addition to them, there are also infinite ordinals: the smallest among them is the ordinal type of natural numbers (finite ordinals), which can even be identified with the set of natural numbers itself (indeed: the set of natural numbers is closed down and, like any set of ordinals, is completely ordered , - therefore, it can be identified with the corresponding ordinal number, which exactly corresponds to the definition of ).

Schematic representation of an ordinal. This is indicated by the site https://intellect.icu. Each bar corresponds to an ordinal number of the form , where and are natural numbers.

Perhaps a more intuitive idea of ordinal numbers can be obtained by considering a few of their first representatives: as mentioned above, the set of ordinals begins with natural numbers After of all natural numbers, there is the first infinite ordinal , followed by , , , and so on . (The exact meaning of addition will be defined later, so consider this notation as a simple notation) After all such numbers are (i. e.), , , and so on, then , and after it - . Further, the set of ordinals that can be written as , where and are natural numbers, must also have a corresponding ordinal number: such a number will be . It will be followed by , ,…, , then - much later - ("epsilon-zero") (the examples listed give an idea of relatively small counting ordinals). This process can be continued indefinitely. The smallest uncountable ordinal is the set of all countable ordinals and is denoted by .

Definitions

Ordinal numbers are usually denoted by lowercase Greek letters. This article adheres to such notation.

Well-ordered sets

Every non-empty subset of a well-ordered set contains a least element. Subject to the axiom of dependent choice, this is equivalent to saying that the set is linearly ordered and does not contain infinitely decreasing sequences—the latter formulation is probably easier to visualize. In practice, the importance of the concept of well-orderedness is explained by the possibility of using transfinite induction, the main idea of which is that any property that passes from the predecessors of an element to itself must be satisfied for all elements (included in a given well-ordered set). If the computational states (of a computer program or game) can be completely ordered so that each subsequent step is "less" than the previous one, then the computational process is guaranteed to be completed.

Further, we do not want to distinguish between two well-ordered sets if they differ only in "the labeling of their elements", or, more formally, if the elements of the first set can be correlated with the elements of the second in such a way that in an arbitrary pair of elements of one set, the first less than the second if and only if the same relation holds between their corresponding partners from the second set. Such a one-to-one correspondence is called an order-preserving isomorphism, and two well-ordered sets are called order-preserving isomorphic, or similar to (such similarity is obviously an equivalence relation). If two well-ordered sets are isomorphic with preservation of order, then the corresponding isomorphism is unique: this circumstance allows us to perceive the mentioned sets as practically identical and serves as the basis for searching for a “canonical” representation of isomorphism types (classes). Ordinal numbers not only play the role of such a representation, but also provide us with a canonical labeling of the elements of any well-ordered set.

In other words, we want to introduce the concept of an ordinal as a class of isomorphisms of well-ordered sets, that is, an equivalence class based on the "order-preserving isomorphism" relation. With this approach, however, there is one technical difficulty: the equivalence class defined in this way turns out to be too large to fit under the definition of a set in terms of the standard Zermelo-Fraenkel formalization of set theory. However, this complexity does not create serious problems. Ordinal we will call the ordinal type of an arbitrary set in such a class.

Definition of ordinal numbers as equivalence classes

In the original definition of an ordinal number, which can be found, for example, in Principia Mathematica, the ordinal type of a well-ordering is understood to be the set of all well-orderings similar to it (isomorphic with order preservation): in other words, an ordinal number is indeed an equivalence class of well-ordered sets. In ZFC theory and related axiomatic systems of set theory, such a definition is unacceptable, since the corresponding equivalence classes are too large to be considered sets. However, this definition can be used in type theory and Quine's axiomatic set theory (New Foundations), as well as other similar systems (in which it allows us to formulate an alternative and rather unexpected way of resolving the Burali-Forti paradox about the largest ordinal number).

Von Neumann definition of ordinal numbers

Instead of defining the ordinal as the equivalence class of well-ordered sets, we identify it with a particular set that serves as the canonical representation of this class. Thus, an ordinal will be some well-ordered set, and any well-ordered set will be like exactly one ordinal number.

Von Neumann's standard definition is: any ordinal is a well-ordered set consisting of all ordinals less than its . In symbolic notation: . ^{^{More formally,}}

A set is an ordinal if and only if it is strictly well-ordered by a relation and each element S is simultaneously its subset.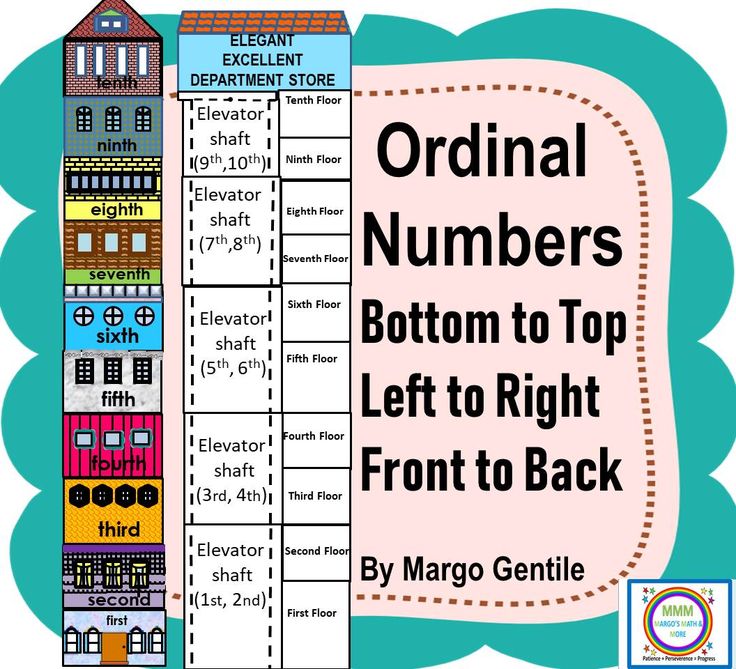

Note that natural numbers are ordinals according to this definition. So, 2 belongs to 4 = {0, 1, 2, 3} and at the same time is equal to {0, 1}, that is, it is a subset of {0, 1, 2, 3}.

Using transfinite induction, one can show that any well-ordered set is similar to exactly one ordinal—in other words, one can establish a bijective order-preserving correspondence between them.

Moreover, the elements of any ordinal are themselves ordinals. If and are arbitrary ordinals, then it belongs if and only if it is a proper subset of . Further, for any ordinals and one of the relations is satisfied: either , or , or . Thus, any set of ordinals has a linear order and, moreover, is well ordered. This result is a generalization of the well-ordered natural numbers.

It follows that the elements of an arbitrary ordinal exactly coincide with ordinals strictly less than . Each set of ordinals, for example, has a supremum, which is an ordinal equal to the union of all ordinal numbers contained in this set. By virtue of the union axiom, such an ordinal always exists, regardless of the size of the original set.

The class of all ordinal numbers is not a set. Otherwise, it would be possible to prove that such a set is itself an ordinal number and, therefore, its own element, which contradicts strict ordering. This statement is called the Burali-Forti paradox. The class of ordinal numbers is denoted in various ways: "Ord", "ON", or "∞".

An ordinal number is finite if and only if it is well ordered not only by the natural but also by the opposite order - this condition is satisfied if and only if each of its subsets contains the largest element.

Other definitions

In modern mathematics, there are other approaches to the definition of ordinal numbers. Thus, when the axiom of regularity is satisfied, the following statements about the set x are equivalent:

x is an ordinal number,

x is a transitive set with trichotomy relation

x is a transitive set linearly ordered by the relation . For a set, we define a two-place relation consisting of pairs such that or . A set is called transitive if it follows from . A set is called an ordinal if it is transitive and is a well-ordered set.

x is a transitive set whose elements are also transitive sets.

The enumerated definitions are inapplicable in set theories without the foundation axiom. In theories with urelements, the definitions need to be clarified, since urelements are from among the elements of an ordinal number.

Transfinite sequence

If is a limit ordinal and is some set, then a -indexed sequence of elements is a function from to . Definition 9 introduced in this wayThe 0521 transfinite sequence or the sequence indexed by ordinals is a generalization of the notion of a sequence. The usual sequence corresponds to the case .

Properties

If is an ordinal number, then each element is an ordinal number.

Exactly one of the following relations holds for any:

Any set of ordinal numbers is well ordered by the relation (in particular, any ordinal number considered as a set is well ordered by the relation ), and is the smallest element of the set , is an ordinal greater than or equal to any of the elements of the set . The expressions and for ordinal numbers are equivalent. The following assumes that ordinal numbers are compared using the relation

For any well-ordered set, there exists a unique ordinal number isomorphic (in particular, for any set of ordinal numbers, there is a unique ordinal number isomorphic to it).

Any coincides with the set of all ordinal numbers less than .

The leading segment of any ordinal is an ordinal.

The empty set is the smallest ordinal number (which means that it is an element of any other ordinal number).

is called unlimited if either it is equal to , or there is an immediately preceding it, in other words, if it exists but no other ordinal number can be inserted between them. which turns out to be consistent with the notation for the sum of ordinal numbers).

Ordinal numbers that are not non-limit are called limit ordinal numbers (sometimes also referred to as limiting ordinal numbers).

The set of all finite ordinal numbers is isomorphic to the set of non-negative integers, and the same notation is used for them as for integers. In this case, the operations of addition, multiplication and exponentiation for ordinal numbers are transferred to the corresponding operations for integers. Several first ordinal numbers:

The set of all finite ordinal numbers is denoted It is the smallest limit ordinal number and the smallest infinite (namely, countable) ordinal number. The next serial number is

The finite condition can be written as or, which is the same,

There is an infinite set of ordinal numbers, but there is no set of all ordinal numbers. In other words, the collection of all ordinal numbers is a proper class.

Each set of ordinal numbers is bounded from above and has a least upper bound, which is denoted by

If — limit ordinal or , then 9 otherwise0022
The least upper bound of a countable set of countable ordinal numbers is countable ^.

Each ordinal number α has a unique representation in Cantor normal form , where , , and are ordinal numbers. The form allows you to find expansions like the following:

Ordinal arithmetic

Operation definitions

The sum of ordinals is recursively defined as follows:

where the third rule applies when is the limit ordinal.

Using the same notation, we define the operation of multiplication:

Using the same notation, we define the exponentiation operation:

Properties of operations

Ordinal addition is noncommutative; in particular

Ordinal addition is associative: which allows you to write the sum of several terms without parentheses.

The sum increases with the growth of the right term and does not decrease with the growth of the left term: it follows from

If then there is a single ordinal for which

Multiplication of ordinal numbers is non-commutative; in particular

Multiplication of ordinal numbers is associative: which allows you to write the product of several factors without parentheses.

Addition and multiplication are left distributive:

If the arguments are finite, addition, multiplication, and exponentiation are converted to the corresponding operations for integers (with final results).

If the arguments are countable, the results of addition, multiplication, and exponentiation are also countable.

See also

Cardinal number

TRANSFINITE NUMBER

In general, my friend, you overcame reading this article about ordinal number .
Learn more

Adjective definition for 2nd grade

Sight word examples

Jack and magic bean

Halloween scavenger hunt list

Shape theme preschool

Learning to write alphabet letters

Reading skills children

What the moon looked like on my birthday

Math for class 1

Book rhyming words

What syllables means