Teach first grade addition
Addition Strategies for First Graders
Home » Blog » Operations » Addition » Addition Strategies for First Graders
Written by: Angie Olson
365 shares
- Share194
- Tweet
First grade is the year that students are developing their foundational mathematical skills. It is critical that when learning how to add numbers, our students are learning and understanding HOW to use a math algorithm to find an answer and also able to explain WHY they are doing so. When I teach my students addition, they have a solid understanding of numbers and place value first. Then I introduce different addition strategies. After some practice with these strategies, the focus can shift to memorization of facts. This, of course, comes later.
Some strategies that I like to use when teaching addition are:
(these are all covered in the First Grade Addition Interactive Notebook)
1. Zero Facts
2. Turn-Around Facts
3. Counting On
4. Doubles Facts
5. Using Fingers
6. Using Manipulatives
7. Near Doubles
8. Make a Ten
9. Part Part Whole
10. Combining Numbers
11. Tally Marks
12. Ten Frames
13. Fingers
Download Addition Strategies Flip Flaps HERE
Another important component to teaching any new unit in math is to teach the vocabulary words that go with the concept. This particular interactive math notebook activity includes 10 vocabulary words with definitions. You could have your students glue their definitions under the vocabulary word or write the definition themselves.
Download Addition Vocabulary Flaps HERE
This First Grade Addition Strategies Notebook includes all of the strategies you read from above along with activities for practice of these addition strategies. I believe most first graders benefit from using manipulatives when learning a math skill so these interactive notebook activities were designed to accompany some of the most basic math manipulatives such as dice, counters, dominoes, etc.
Download All Things 1st Grade Interactive Notebooks HERE
My favorite part about this First Grade Addition Strategies Notebook is the word problem story mats. Word problems seem to always be a trickier concept for students to master so I knew that I wanted to find a way for students to practice this skill in a practical way. That’s when these word problem story mats came to life!
I love that there are pictures provided for each story or I can use any math manipulative that I have laying around my classroom. These word problem story mats can also be easily differentiated. For the struggling student, I would use these as a part of their math center. I would provide the story prompt and a limited number of counters. I can also see this being used with at grade level students by having them work with a partner to determine a story, place counters on the story mat, and write the addition sentence to go with the word problem. For the advanced first graders, I would provide the story mats and an increased number of counters. Then they would work independently or with a partner to write a word problem of their own along with the addition sentence to go with the word problem. The First Grade Addition Notebook includes 5 different stories with counters.
Then they would work independently or with a partner to write a word problem of their own along with the addition sentence to go with the word problem. The First Grade Addition Notebook includes 5 different stories with counters.
Download Word Problem Story Mats HERE
Feel free to use the image below to save this post to your Pinterest board. Happy Teaching! 🙂
365 shares
- Share194
- Tweet
6 Strategies to Teach Addition
First grade is a crucial point in a student’s mathematical journey. This is when they are developing those foundational skills that they will carry with them throughout grade levels. Our first-graders must know how to add numbers but also explain how they found their answers. To fully understand the concept of addition, our students need to have built their foundation of understanding numbers.
After they have developed those foundational skills, we can give them solid strategies to practice addition skills. Remember, when it comes to teaching strategies to your first-graders, the ultimate goal is to have our students gain the skills to compute math mentally. So, if you are looking for hands-on and interactive ways to teach your first-graders, then you’ve come to the right place.
Remember, when it comes to teaching strategies to your first-graders, the ultimate goal is to have our students gain the skills to compute math mentally. So, if you are looking for hands-on and interactive ways to teach your first-graders, then you’ve come to the right place.
Zero Facts
I know it sounds silly that I am mentioning this one, but your students must understand that zero added to a number doesn’t change it. This strategy is almost a check-off-the-box strategy. Make sure they know it and move on.
Ten Frames
Ten frames are another excellent tool in teaching addition to first-graders. Ten frames are another way to help students visually add numbers. I like using two separate ten frames with counters and having students practice addition problems—a great way to give students independent practice. Ten frames give students a hands-on approach to working with numbers. Within ten frames, you can teach your students about doubles, doubles+1, and make a ten.
Counting On
Counting on is a pretty simple concept, but it’s a crucial one for mental math. For instance, 4+6, tell your students to put 4 in their head and count up. You can use this with a number line for a visual component.
Turn Around Facts
Our first-graders must understand that flipping the addends doesn’t change the sum when it comes to addition. A great way to teach this concept is with counters, dominos, and worksheets. Once students grasp this concept, they can continue to move forward with more complex addition problems.
Manipulatives
Can you teach first-grade without manipulatives? The answer is no! Using manipulatives in the first-grade classroom is one of the most critical aspects of teaching addition. Use, counters, bears, buttons, beads, erasers, or anything else hanging out in the cabinet full of a ton of stuff.
Manipulatives help students explore using a hands-on learning method, and they can visually see the items to assist them in understanding mathematical concepts. And, students learn better when they are engaged with the material, and manipulatives increase engagement.
And, students learn better when they are engaged with the material, and manipulatives increase engagement.
First-graders often struggle with understanding that they can combine two separate numbers to make a larger quantity. Counting with manipulatives is the perfect way to teach first-graders to add numbers together.
I love using manipulatives in my classroom because it’s a tangible way to understand mathematical concepts. While manipulatives aren’t a traditional strategy, they are an essential tool needed in many strategies.
The Extras
Again, these last two aren’t official mathematical strategies, but they are used to teach addition in my classroom. Most importantly, using games. Anything in game form is a win with my first-graders. I love using games because it allows my students to practice, work with partners, and apply their knowledge.
Lastly, I love using digital resources for all different avenues like independent work, early finisher activities, and homework. We accumulated a ton of resources from distance learning, so why not utilize them? Digital resources are just another hands-on way to apply and practice with addition.
We accumulated a ton of resources from distance learning, so why not utilize them? Digital resources are just another hands-on way to apply and practice with addition.
Another tool that I have learned throughout the years is to make an anchor chart of the various methods that your students learn best from and hang it up where everyone can see it. Anchor charts are lifesavers and they are a vital tool for our young learners.
There are many strategies in teaching addition, but it’s important to remember that we do not want our students to memorize these concepts. We want them to know and understand the strategies so they can successfully use and apply them. I have found a ton of value in teaching these strategies during small groups. While we review and practice whole group, I have found it way more beneficial to teach these strategies to a smaller group of students. What is your favorite strategy to teach addition?
How to teach a child math 1
We help clarify words from life and basic scientific disciplines.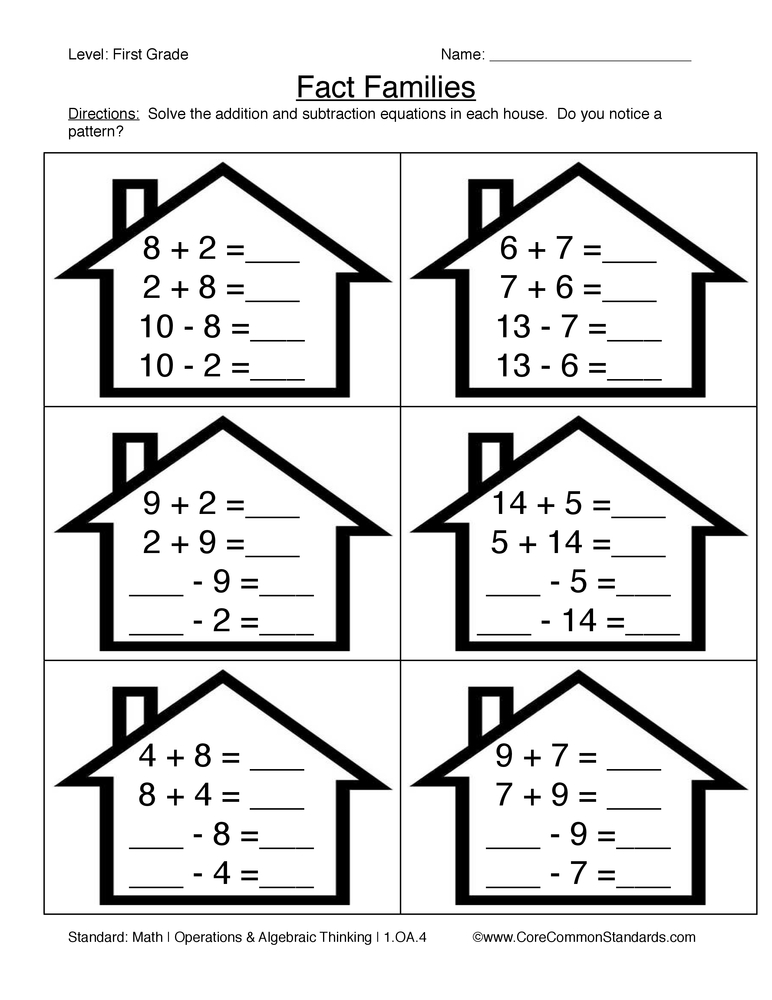 This section is dedicated to mathematics. Our basis:
This section is dedicated to mathematics. Our basis:
Problems in mathematics mean there are misunderstood words.
The more problems, the more fundamental words are not understood (or not fully understood). We took a math textbook for grade 1 and found a few fundamental words. And we help you figure it out.
Clarify words with us and you will be surprised how the understanding of the subject will increase both in schoolchildren and in adults. 9Ol000
The results of our word clearing for mathematics Grade 1
(yes, as it becomes clear, as it should be, we have new understanding :) )
Thus, subtraction, like counting in general, depends on the attention paid to each unit of the set. Only during the calculation of the amount and quantity, we add attention to an increasing number of units. And during subtraction, we remove attention from those units that are no longer there.
Hence the conclusion: the more attention a person has, the better he counts real objects, the better he operates with numbers.
Therefore: problems with counting and numbers means that you need to increase the amount of attention.
A misunderstood word absorbs attention. The understanding of the word grows as it becomes clearer. The more words are clarified, and the more complete, the more free attention can be directed to usefulness.
As we have calculated, there is an algorithm for calculating the number, sum and difference.
Algorithm for calculating the amount and quantity:
We pay attention to each unit of the set, and give it a number. The largest number is the quantity or amount you are looking for.
Example: five apples plus five loaves. Total give the numbers: 1,2,3,4.5,6,7,8,9,ten. 10 is the largest, so the sum is 10.
The subtraction algorithm is the other way around:
We go from the largest number and name the number of each one that we remove. The largest remaining is the result of the subtraction.
Example: subtract three from six pears. We count: six, five, four. The highest remaining number is three. So the result of subtraction is three pears.
We count: six, five, four. The highest remaining number is three. So the result of subtraction is three pears.
Also interesting: counting in particular and mathematics in general are areas that reflect time . For example, there were five apples, now there are six - moving into the future. And negative numbers (it was -2 apples, that is, a debt of 2 apples, that is, a subtraction in the future) - movement from the future to the present. Therefore, the sign = in mathematical notation is a very strong convention. Hoya would be because in the universe there are no absolutely equal objects at the same time. Though on a molecule, but they differ.
So, instead of the = sign, it is more logical to use the → sign. It turns out
there were five apples + five apples were once added → after counting in the present tense it became 10 apples.
Or there were 8 apples minus 3 apples → after counting, there are now 5 apples.
There is no deceptive equality in such a notation.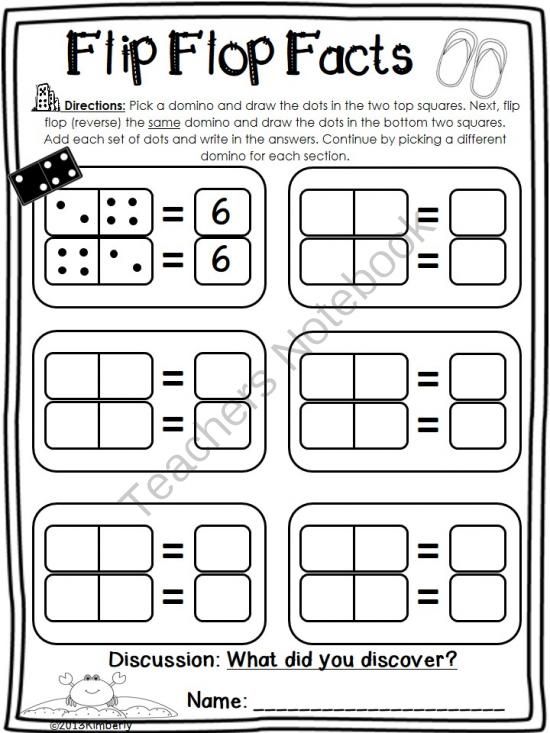 There is logic. And it becomes clear zero.
There is logic. And it becomes clear zero.
After all, zero is a complete nothing, there is no length, no width, no height, no particle, no wave. This does not happen in the physical universe.
So the example 5 crows - 5 crows = 0 crows is wrong. After all, ravens have not ceased to exist. Even if they were killed and burned, there were ashes, energy, smoke, memory. More logical notation:
5 crows - 5 crows → 0 crows in this place, in this form and right now.
Somehow these crows exist. Even if under the guise of tobacco chickens :)
From this point of view, the law of rearranging the terms and maintaining equality does not work, because the earlier event comes first in the calculation.
You can also ask: “And what, according to your algorithms, you need to count on your fingers? At 10 - not bad, but at 1000 - a nightmare!
Completely agree with you. Therefore, in school they do not teach counting as such, not addition and subtraction.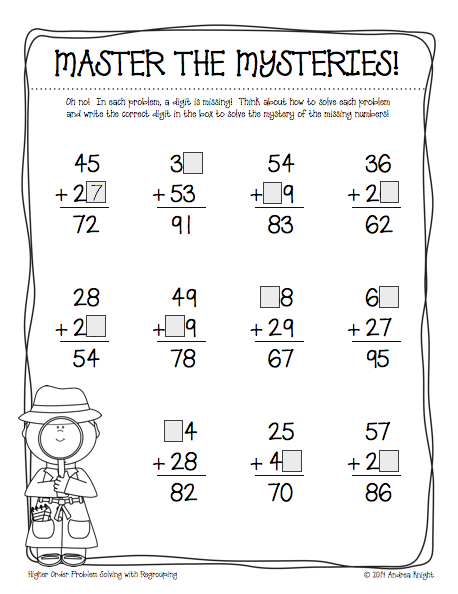 They teach one of the number systems - the decimal system plus fast operations with it. Like addition in a column, subtraction in a column, quick counting techniques in the decimal system.
They teach one of the number systems - the decimal system plus fast operations with it. Like addition in a column, subtraction in a column, quick counting techniques in the decimal system.
In addition to school columns, there are many other quick counting techniques and addition-subtraction methods. For example, in ancient times, the Chinese used a column, but they drew not numbers, but sticks:
| | | | |
this is soup| | | | | | |
| | | | | | | | | | | |
That is, 5 + 7 = 12.
Or there is an alternative method of quick counting in the mind - the Trachtenberg method, described in the book "The Trachtenberg Quick Counting System". Perhaps children should be taught IMMEDIATELY to count quickly.
But be that as it may, the basis of mathematics is precisely the counting of objects, the measurement of real-life quantities. Therefore, at least in the first grade, you need to devote considerable time not to tricks, but to the basics - paying attention and operating with it.
But, again, these are OUR understandings when clearing the words. Clarify - and find your own! Write examples with words in the comments to the articles - and we will correct them if necessary :)
Good luck with word clearing in mathematics grade 1!
Mathematics lesson in grade 1 "Addition and subtraction of the type ... + 3, ...
9000 30107 Director of MKOU "Tarumovskaya "Secondary School"
__________________ / Gaitemirova MN /
4
"Addiation 908 908 908 908 908 908 908 908 908 908 908 90LA and subtraction □ + 3, □ – 3 »
Teacher 9 80107 Abdullaeva R . M .
M .
2019-2020 CCA
907 Subject: Addition and subtraction of the form □ + 3, □ - 3
Purpose : to teach perform addition and subtraction of the form □ +3, □ - 3, form computational skills, the ability to solve problems, instill an interest in mathematics.
Expected results: students will learn to solve examples of the form +3, - -3; evaluate yourself, the limits of your knowledge and ignorance.
Lesson progress:
I. Organizational moment.
Guys, join us today guests have come, look at them now, say hello, give a smile.
Up sun for a long time,
to our window,
On the lesson rushes us
Mathematics now.
We wish good luck to everyone -
work at a good hour!
Who set to do a good job in the lesson, clap your hands. Well done!
Well done!
Tell me what you need study math? (children's answers)
Well, now let's get down to business.
Mathematics waiting for us,
Let's start verbal account
II. Update knowledge.
Today we are going to visit you.
To whom? (surprised)
Look at slide and you will understand. slide (winter-winter)
The winter itself is very beautiful, therefore Everything around is glittering and sparkling.
- Tell me, what is the winter like? (blizzard, cold, frosty, harsh, fierce, icy, unexpected, snow-white.)
Who will meet us in winter, we will know if we complete the first task. slide
Look on the slide and say how the examples are similar. (Add or subtract 1)
Let's remember what it means to "add one"?
What does "subtract 1" mean?
Read examples in different ways.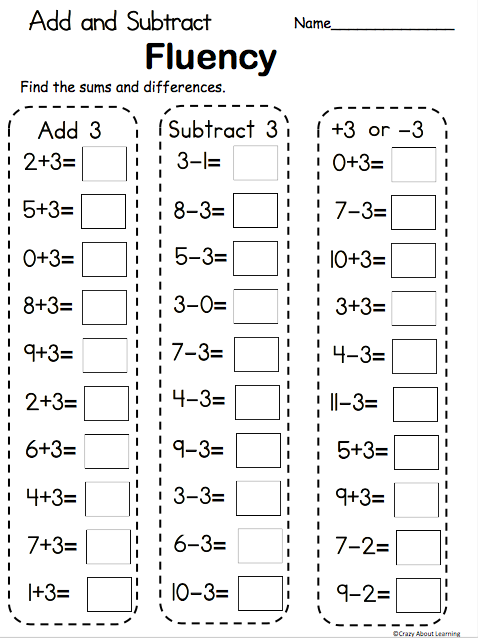
Read what you got.
6, 7, 2, 3, 9, 4, 8, 5
How are the numbers arranged? ( in disorder)
Put the numbers in order increase. slide
What are these numbers? (unambiguous)
Why did you do this task? (to remember that + 1, we call the next number when counting, and - 1, previous)
Guys, what numbers are missing? Where they are? (they call 0.1 and 10 )
What can you say about the number 10? (two digits)
Name , please:
- neighbors of number 5;
- name a number that is greater than 7 by 1;
is a number that is less than 6 by 2;
is a number that is 2 more than 3;
is a number that is greater than 5 by 2.
Well done, every digit, letter matches. slide
The clue is on the slide.
2 - C 4-E 6-O 8-I
3-N 5-G 7-B 9-K
Read the resulting word, and you will know who is coming to us. slide
slide
Coming to us ... (snowman) slide
snowman prepared for you tasks. Who will cope with them will receive a gift.
I So let's continue our lesson.
To gift receive
Need try,
the lesson is not to sit.
Better study.
The next task from the snowman
Winter, frost, cold. To blind snowman we put on our hands?
Let's solve the problem.
1. Tasks in verse.
Oh yeah master squirrel!
Knitting for children mittens.
Knitted three balls,
Two are still lying.
Who has the answer ready,
How many does she have balls? (5)
Guys, you know that there are birds that winter with us, do not fly away to warmer climes? How can we help them?
2. Four bullfinches on were sitting in the feeder.
Three more bullfinches arrived.
Our snowman counted bullfinches.
How many birds are there?
Answer hurry up (7)
Who likes sledding? Want to ride down the hill with the breeze? slide
We go up the hill. Consider an example. slide
4 + 2 8 - 2
7 + 2 5 - 2 9002 - 9003 added? Did you read? How add the number 2?
Have you had enough? Say we're good did you ride? Prove it!
III. Self-determination to activity.
The snowman offers to fill in the blanks.
What did you notice? (added the number 3)
What is the name of the action when we adding one number to another? (addition)
What do we call an action when we are from the same subtract other numbers? (subtraction)
- How to share 3 apples between the Snowman and the Snow Maiden?
- How many apples do you need to add to make the Snowman have 3?
- How many apples need to be added so that the Snow Maiden has 3?
- Finish statement:
3 is 1 and .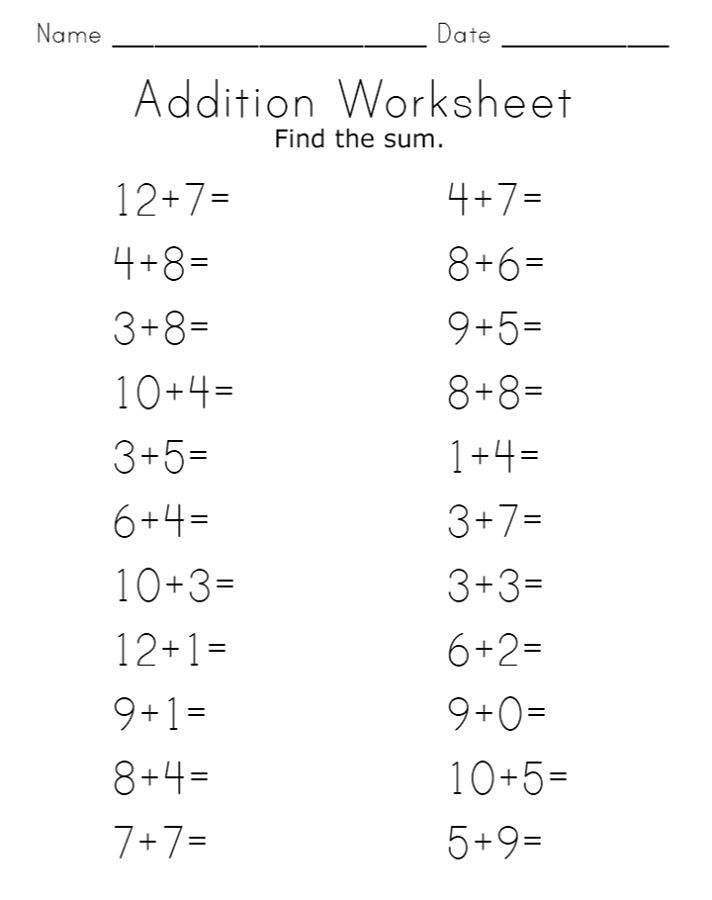 .., 3 is 2 and ...
.., 3 is 2 and ...
- What do we are we going to study in class today? (Add and subtract the number 3.)
Physical education minute.
Yes one game for you:
I I will start poetry now,
I I'll start, you continue:
in chorus answer together:
it's snowing in the yard,
Coming soon holiday ... (New Year)
Softly glowing needles
Coniferous the spirit comes from ... (trees)
branches slightly rustle,
Beads bright... (shine)
And decorating the top
There shining as always
Very bright, big,
Five-winged … (star)
Long-bearded and red nose
Our cheerful ... (Santa Claus)
IV. Work on the subject of the lesson.
Practical Job. US
it is necessary to add 3 to the number 6. We still do not all know how to do this. How are you would you like to make this job easier? (it is necessary to add the number 3 in parts). Put 6 apples.. How can you add 3 in parts? (first 1, then another 1, and then another 1). How can this be written down? 6+1+1+1. How else? (Put 2 apples first, then 1-6+2+1). Is there another way? (there is, you must first put 1 apple, and then another 2 - 6+1+2).
Conclude: how can you add number 3?(…+1+1+1, or…1+2, or…2+1).
7 - 3 As can you subtract 3 in parts? (first 1, then another 1, and then another 1). Like this can you write it down? 7-1-1-1. How else? (Remove 2 apples first, then 1-7-2-1). Is there another way? (there is, you must first remove 1 apple, and then 2 more - 7-1-2).
Conclude: how can you subtract number 3? (…-1-1-1, or…-1-2, or…-2-1).
v. Fastening studied material.
1. Work by textbook.
- Read the question on page 104, which we must answer. (How can you add 3?)
- Who can already answer now?
- Consider examples and pictures for them. Let's explain.
#1. For every row example, solve and explain.
#2. -What do you need do? (put signs <> or =). Examples are explained.
No. 3. – Compose drawing tasks:
“Katya had 5 envelopes. She bought 3 more envelopes. How many envelopes did Katya have?
“Yulia had 9 postcards. She gave 3 postcards to her friend. How many postcards does Yulia have left?
#4 Read the task.
- What is known from conditions of the problem? What else is known?
- What does it mean to become 3 less?
- Read question.
- How to find out how many berries are there?
No. 5 Likewise.
№6 To find sum, you need to add the terms. 6 + 2
No. 7 geometric figures are given. What are we about them know? (these are broken closed lines, polygons).
VI Physical minute. Tired? Let `s have some rest. (for eye - snowflakes)
VII Work in a printed notebook.
№1 Read the problem.
- What is known from the condition of the problem?
- Draw 5 circles.
- What else is known?
- What does it mean to buy a pencil for 3 rubles? (Spent, so removed, decreased.)
- How to show this in the picture? (cross out)
- Find and read the question.
- Write down the solution of the problem in your notebook.
- Who wants to read their decision? 5-2=3(p.)
- What is missing in our problem? (Answer) Write down the answer
№2 - What is known from the condition of the problem?
- Draw 4 circles. (in blue pencil)
- What else is known?
- What do you mean by 2 more?
- How to show this in the picture? (add 2 red circle)
- Find and read the question.
- Write down the solution of the problem in your notebook.