The grapes of math activities
FREE Problem Solving Challenges Based on "The Grapes of Math"
Want to encourage meaningful math talk and problem solving? Try these playful problem solving challenges based on the book The Grapes of Math by Greg Tang!
One of my favorite books is the New York Times Bestseller, The Grapes Of Math by Greg Tang. This hilarious and interactive tale invites students to think outside the box to tackle wacky math riddles. Each challenge encourages new ways to see quantities and count objects. It invites kids to think and ask, “How else can I find the total?” or “What is the most efficient way to count or add or multiply?” These are the kinds of problem solving challenges that will develop and deepen number sense in kids. So if you’re excited to dig in, grab a copy of the book and then extend the challenge with these additional problem solving pages!
*Please Note: Some of the links in this post are affiliate links and help support the work of this site. Feel free to read our full disclosure policy here.*
Although I designed these challenges to be used along with the book, The Grapes of Math, you could use them independently. The key is to encourage creative problem solving and challenge kids to find another way to see the images.
Each page presents a math problem that requires addition. Each could be solved simply by counting the objects one by one, but the point of each puzzle is to try and find a way to solve the problem quicker and easier.
Greg Tang’s picture book, The Grapes of Math, uses silly rhymes and engaging illustrations to help kids learn several helpful problem solving strategies, such as making ten to add more efficiently, looking for groups of numbers to skip count, subtracting to add, and more!
As Greg Tang explains in his introduction,
“The Grapes of Math teaches four important lessons in problem solving.
The first is to be open minded. Children will learn to look beyond the obvious in search of smarter solutions. Second, they are encouraged to think strategically by finding convenient sums that make adding easier. Third, kids are taught to save time by using a variety of skills when solving problems, such as subtracting to add. Finally, children learn to organize information by identifying patterns and symmetries.”
This book is great for visual learners, or for students who like a challenge. Even after finding the right answer, I would encourage you to ask your child (or student) how they arrived at their answer (try to figure out how they saw the picture) and then ask them to figure out another way to solve it. This is a great way to have mathematical discussions and get kids used to explaining their thinking.
And if your kids love The Grapes Of Math as much as we do, they won’t want to stop once the book is finished! So I’ve created some problem solving challenges with addition questions similar to the ones in the book!
Want to learn more about engaging students through meaningful problem solving? Check out my professional development course, Problem Solved: Teaching Math through Problem Solving.
This free download includes 8 pages of unique challenges, as well as an answer key for each page. And although it does not include cute rhymes with helpful hints, hopefully your kids will have some good ideas and be ready to tackle these on their own after working through The Grapes Of Math!
And because these will be printouts that your kids can have (rather than a picture book), I hope you will encourage them to write on each page! It’s often helpful to circle groups of five or ten, or to circle the objects to subtract.
Just be sure they are using pencil, so when you ask them to solve another way, they can erase and start again! 😉
I hope this proves to be a great source of FUN and engaging math learning, and gets your kids excited about exploring new problem solving strategies!
If you’re looking for a similar challenge for younger kids, I recommend starting with dot card visuals and asking “how many?”
And if your kids enjoy this book and the practice pages, be sure to check out some of Greg Tang’s other books:Math For All Seasons: Mind-Stretching Math Riddles
Math-terpieces: The Art of Problem-Solving (I especially love this one, because I love art history!)
Math Potatoes: Mind-stretching Brain Food (a little more challenging than The Grapes of Math)
And if you want to see this kind of problem solving play out with a more challenging question, check out this video of 6 year old Autumn solving a finite series problem!
{Click HERE to go to my shop and download “The Grapes of Math” Problem Solving Pages!}Enjoy!!
Never Run Out of Fun Math Ideas
If you enjoyed this post, you will love being a part of the Math Geek Mama community! Each week I send an email with fun and engaging math ideas, free resources and special offers. Join 163,000+ readers as we help every child succeed and thrive in math! PLUS, receive my FREE ebook,
5 Math Games You Can Play TODAY, as my gift to you!
Join 163,000+ readers as we help every child succeed and thrive in math! PLUS, receive my FREE ebook,
5 Math Games You Can Play TODAY, as my gift to you!
Exploring Your Own Thinking | DREME TE
Print resource
Print resource or save as PDF
Print feature not currently compatible with Firefox.
Print resource
Print resource or save as PDF
Print feature not currently compatible with Firefox.
- PreviousCounting for Adults
- NextAdditional Counting Readings
Activity for Teacher Educators
One technique often used in math workshops is to have prospective or practicing teachers explore their own mathematical thinking. Basically, the method is first to give teachers a problem to solve, often a non-traditional problem, second ask them how they solved it, and third discuss the methods and what the experience means for education. In this way, teachers can learn that they use some interesting, non-conventional methods. Further, the experience may help them understand that children, too, may solve problems in non-conventional ways, and that learning about children’s methods and using them to foster education can be extremely valuable.
In this way, teachers can learn that they use some interesting, non-conventional methods. Further, the experience may help them understand that children, too, may solve problems in non-conventional ways, and that learning about children’s methods and using them to foster education can be extremely valuable.
For these reasons, we developed the following activities for our graduate school students in a course called The Development of Mathematical Thinking. The activities are taken from The Grapes of Math: Mind-stretching Math Riddles (Tang, 2001). Students in the class were required to solve three different riddles and to explain their thinking.
Solve the following riddles. What were some of the addition and/or subtraction strategies that you used? Explain your mathematical thinking. Provide a snapshot and/or video as evidence of your mathematical thinking.
Our graduate students were working on our Mediathread web platform that enabled them to open the three math puzzles and then submit written answers, including pictures of their solutions, or even videos of how they solved the problems. We have selected some student responses that illustrate the different kinds of thinking the students used to solve the problems. Imagine a class discussion of these strategies and their implications for education.
We have selected some student responses that illustrate the different kinds of thinking the students used to solve the problems. Imagine a class discussion of these strategies and their implications for education.
The three math puzzles are shown below, followed by some student responses, which encompass a very wide range of experience.
Math Puzzles
The Grapes of Math (Tang, 2001)The Grapes of Math (Tang, 2001)The Grapes of Math (Tang, 2001)
Student Response Samples
This student used a grouping strategy for the grapes, as is clearly explained. In the second solution, for the snail problem, she added the fives but forgot to subtract the three missing snails. The student simply counted all the snails and did not do any form of grouping. This could have been a result of the prompt phrase “consider where a snail should be!” Under one interpretation, the student may think there should be 25 because a snail should be where it is unseen, but a different student might interpret that to mean that she pay attention to the lack of a snail and subtract it. People often solve the problems they perceive rather than the problems the authority intends to present. It is for this reason that having prospective teachers engage in a variety of these types of problems can be useful in informing their understand of mathematics and children’s thinking.
People often solve the problems they perceive rather than the problems the authority intends to present. It is for this reason that having prospective teachers engage in a variety of these types of problems can be useful in informing their understand of mathematics and children’s thinking.
This student did a different grouping strategy for the grapes problem, adding each group of seven to a group of three and then adding the tens. This is very sensible. In the snail puzzle, the student saw that there were five rows of five and then did the necessary subtraction. She solved the fish school puzzle by adding successive rows, getting to 10 and then continuing the addition.
This student used a strategy similar to that of the previous student for the grapes problem. She said that she counted on three more from seven to get the 10, but we are skeptical of her account. She probably knew the number fact 7 + 3 = 10. But it doesn’t matter. The main idea is grouping the tens. Her answer to the snail parade is distinctive. Instead of getting the possible total of 25 and then subtracting, she cleverly regrouped the rows by taking two snails from the fifth row and putting them in the first row, and the remaining two from the fifth row and putting them into the third row. She then added the rows as described. (Of course she could have just multiplied five by four.)
Instead of getting the possible total of 25 and then subtracting, she cleverly regrouped the rows by taking two snails from the fifth row and putting them in the first row, and the remaining two from the fifth row and putting them into the third row. She then added the rows as described. (Of course she could have just multiplied five by four.)
Summary
Hopefully, this gives you a sense of the variety of responses to this type of activity.
This material can be used as a springboard for discussion in a class or a teacher workshop. The main point is that students used many different methods to solve the three how many questions. The least efficient is simply counting everything, a method used by two students—at the graduate school level. The other methods involved grouping of one kind or another.
A discussion of these results might involve the following issues (and no doubt others):
- Why count if easier methods are possible?
- The possible value of mental math.
- Several different solution methods are possible for each problem.
- How is it possible for two different methods to yield the same result? Thus, for the grapes problem, one solution is essentially (4 x 7) + (4 x 3) and the other is 4 (7 + 3). How do these methods relate to one another? What does the comparison tell us about the distributive property?
- The development of the solution method is an act of mathematical thinking.
- It is possible for adults to make mistakes on apparently simple problems.
- And finally, and most importantly, what are the implications for teaching children how many? One answer should be abundantly clear: we need to teach children to think in mathematically creative ways.
- Does this experience suggest anything about the value of discussions in the classroom? For example, can children learn something important about math from seeing that others use a variety of solution methods?
Reference
Tang, G. (2001). The grapes of math: Mind-stretching math riddles. New York: Scholastic Inc.
(2001). The grapes of math: Mind-stretching math riddles. New York: Scholastic Inc.
Resource Type
Activity
:: More... | :: Department History | ||||||
| | M.F. Bockstein. Contribution to topology. In 1947, Meer Feliksovich Bokshtein was invited to the post of professor at the Department of Higher Mathematics at MATI. M.F. Bokshtein graduated from Moscow State University in 1936, in 1939 - postgraduate studies at Moscow State University. His first scientific work, published at 1939, was devoted to the theory of differential equations, but all his subsequent work concerned topology and homological algebra. At first, he paid much attention to topology, which was well developed in Moscow, which at that time was one of the world centers of topological science. In modern topology and homological algebra, the construction introduced by M.F. Bockstein and is now called the Bockstein homomorphism all over the world. Now it seems to topologists very simple and natural (almost like 2 + 2 = 4), it is presented in almost every textbook on topology and homology theory. The Bockstein homomorphism in its simplest form allows one to construct long exact sequences of homology (and, in the dual version, cohomology) for arbitrary exact sequences of three different groups of coefficients, acting as a link between the homologies (cohomologies) of adjacent dimensions. Sam M.F. Bokshtein, like many mathematicians of the older generation, was a great lover and connoisseur of music. There is a story about him. In those days, lectures on mathematics were held in the assembly hall (in the building on Ulyanovsk 13, where the military department later settled). There was a piano in the assembly hall, and during the lecture, Meer Feliksovich sometimes, after formulating the next theorem, approached the piano and, with the words "this theorem sounds like this," performed a musical passage. R.E. Vinograd, B.F. Bylov. Contribution to the study of systems of linear differential equations. Systems of linear differential equations have been one of the most important branches of mathematics for the last two or three hundred years. This is due to the fact that, on the one hand, any system of differential equations can be transformed with a certain accuracy into a linear system (i.e. linearized), and on the other hand, by the fact that for systems of linear differential equations it is possible to prove many important and very interesting results, whose analogues for systems of arbitrary (nonlinear) equations are either incorrect or have not yet been proved. As for the importance of the theory of differential equations itself, its exceptional position in mathematics is associated with a huge number of effective applications to solving practical problems in almost all areas of science (including the humanities) and technology. One of the very interesting parts of the theory of systems of differential equations is the study of the behavior of solutions of these equations and their systems "at infinity", i. There are two main research methods in the theory of stability. Both of them were introduced by A.M. Lyapunov and are called the first and second Lyapunov methods. The second Lyapunov method is based on the construction of the Lyapunov function; it has been widely used in solving many applied problems and is even described in many textbooks for universities. As for the first method, it is based on the use of characteristic numbers or, as they are called in the second half of the 20th century, characteristic indicators. This method is not so widely used so far, which is due to the fact that its applications encounter significant mathematical difficulties (in particular, it is very difficult to calculate the characteristic exponents themselves). Characteristic numbers (exponents) are some functions on the space (finite-dimensional vector space) of all solutions x(t) of systems of linear differential equations. In the 50s and 60s one of the centers for the study of characteristic exponents was Moscow, and, in particular, MATI, where Robert Elyukimovich Vinograd, a well-known specialist in the theory of differential equations, worked since 1954. He graduated from Moscow State University in 1948, graduate school in 1952, defending his Ph.D. thesis. In 1954 he was invited to MATI for the position of assistant professor. In 1959 he defended his doctoral dissertation on the theory of characteristic Lyapunov exponents. In it, he developed the abstract theory of Lyapunov exponents, methods for calculating them (the analytical theory of Lyapunov exponents). The classical results of Lyapunov and Perron on correct equations were also generalized. The behavior of indicators for small perturbations of the system was also considered. In Moscow, other mathematicians also dealt with these questions. In particular, it was V.V. Nemytsky, in co-authorship with whom (as well as with D.M. Grobman and B. Since 1956, Boris Fedorovich Bylov worked at MATI. He graduated from Moscow State University in 1950, in 1954 he defended his Ph.D., and in 1966 - his doctoral dissertation. His interests lay in the field of differential equations, their stability and reducibility. B.F. Bylov worked as the head of the department of higher mathematics at the MATI branch in Stupino. N.P. Tarasov. Since 1960, Nikolai Petrovich Tarasov, a well-known teacher, author of the book "A Course in Higher Mathematics for Technical Schools", which went through 17 editions (its first edition appeared in 1935, and in 1975 the 17th was published) was translated into Romanian and (by several editions) into Bulgarian. V.F. Krotov. Contribution to the theory of optimal control. From 1968 to 1972 the department was headed by Vadim Fedorovich Krotov. He graduated from Moscow State Technical University. B.K. Kucherov. 1974 to 1982 The department was headed by Doctor of Technical Sciences Kucherov Boris Kondratievich. He himself was a specialist in applied mechanics, having worked for many years at the Textile Institute, where he defended his doctoral dissertation in 1958. He began his work at the department by inviting young specialists - postgraduate graduates of the Faculty of Mechanics and Mathematics of Moscow State University. In those years, many young teachers worked at the department - specialists in various fields of modern mathematics: algebra (the theory of rings and modules, the theory of Lie groups and algebras, algebraic geometry), general and algebraic topology, function theory and functional analysis, approximation theory, differential geometry, computational mathematics, the theory of differential equations, the theory of dynamical systems, the theory of probability and mathematical statistics, and a number of others. V.A. Vinokurov. Since 1983 Vinokurov Valery Alexandrovich, a graduate of the Physics Department of Moscow State University, has been in charge of the department. With him, several specialists in applied mathematics and mathematical physics came to the department, the applied scientific work of the department was strengthened, the composition of the laboratory was significantly expanded and strengthened. L.A. Ant, I.M. Petrushko. Then the department was headed by Muravey Leonid Andreevich (now he is the head of the Department of Applied Mathematics at MATI, separated from the Department of Higher Mathematics) and Petrushko Igor Melent'evich, both specialists in the theory of differential equations of mathematical physics. Well-known specialists in mathematical physics were involved in the work at the department - professors B.I. Zavialov, A.K. Gushchin and associate professor R.Kh. Galeev. During this period of time, the first personal computers appeared at the department, a display class was formed. Teachers of the department A.A. Zhukov, Yu.A. Kostikov, K.Yu. Osipenko and A.A. Simonov mastered the new technique with great enthusiasm and began to conduct classes with students on personal computers. K.Yu. Osipenko. Since 1996, the department has been headed by Doctor of Physical and Mathematical Sciences, prof. Osipenko Konstantin Yurievich, who came to MATI in 1975 after graduating from the graduate school of the Faculty of Computational Mathematics and Cybernetics of Moscow State University, is a specialist in the field of approximation theory, optimal recovery, extremal problems in the theory of functions of a complex variable. K.Yu. Osipenko is a participant in many RFBR grants (including the "Leading Scientific Schools of Russia" program and a joint international grant with the Chinese Academy of Sciences), he has published more than 70 scientific papers, many of which appeared in major international mathematical journals. In 2000, his monograph on the optimal recovery of analytic functions was published in the USA, commissioned by an American publishing house. He is well known at the international level, participates in many international conferences, in the work of foreign mathematical journals, and is a member of the American Mathematical Society. In 1996, due to the rapid development of computer technology, the department faced the need for a significant renovation and expansion of the computer fleet. In 1997, the department was provided with a display class based on modern computers of a new generation, and the next year, the department itself managed to update the equipment of the second display class. Senior students were recruited to work in the laboratory, by whose efforts both display classes were united into a single local network. The allocation of significant funds for the material and technical support of the department made it possible not only to maintain expensive equipment, but also to continue equipping the department with new equipment. Now you can access the Internet, create your own mail server. The availability of high-performance technology made it possible not only to modernize the computer science course (it began to include modern software products such as Windows98, Word, Excel, Access, as well as a number of mathematical packages), but also to take a fresh look at the classical course of higher mathematics. Work has begun on using in this course new opportunities provided by modern mathematical packages Maple, Mathematica, etc. Together with the Departments of Mathematics of MADI, MIREA, MGRI and the Department of General Control Problems of the Mechanics and Mathematics of Moscow State University, a new mathematics course for technical universities is being developed, which would largely use the opportunities modern computer technology (interactive mode, hypertext, animation, mathematical packages, multimedia tools). The first results of this work were reported in autumn 1998 at the International Symposium on Engineering Pedagogy. Recently, there has been an increased interest in new mathematical courses in many departments. At the department since 1996 a computer seminar began to work under the guidance of prof. K.Yu. Osipenko, whose goal is to help teachers master new technology, teach how to use it for educational and scientific purposes. At 1996-1997 preparatory work was carried out at the seminar, including familiarization of teachers with the basics of computer literacy. Then prof. K.Yu. Osipenko conducted classes on the basics of mathematical editors TeX, LaTeX and AMSLaTeX. In 1998, teachers of the department mastered the possibilities of the global Internet. In 1999-2000 academic year year prof. V.V. Gorbatsevich conducted a computer seminar to train teachers to conduct classes in higher mathematics using modern mathematical packages. In 1997, the cathedral page was created on the Internet (https://www. Since 1996, meetings of the scientific seminar of the department have been held regularly, where teachers of the department introduce their colleagues to the main results of their scientific activities. Many of the newly attracted part-timers begin their acquaintance with the department from a report at a scientific seminar. The seminar is also a good school for young teachers, who have the opportunity to both benefit from the experience of speaking at scientific seminars from their senior colleagues, and get a lot of useful advice regarding their scientific work. Teachers of the department actively participate in international scientific conferences. Over the past few years, teachers of the department have participated in scientific conferences in Austria, Great Britain, Germany, Greece, Israel, Spain, Italy, Canada, Cyprus, China, Poland, France. The teachers of the department won international grants in Great Britain (Yu.V. Selivanov; 10-month grant for research work) and in Italy (E.I. Shifrin; 4-month grant for research work), participated in international INTAS grants (Yu.V. Selivanov) and a joint international grant from the Russian Foundation for Basic Research and the Chinese Academy of Sciences (K.Yu. Osipenko). Together with the Department of Physics and the Institute of Problems in Mechanics, the Department participates in a grant under the program "State Support for the Integration of Higher Education and Fundamental Science for 1997-2000". | ||||||
Synopsis of an integrated GCD with children of a preparatory group for school with general underdevelopment of speech on the topic: "Grapes" | Plan-summary of a lesson on application, modeling (preparatory group) on the topic:
Abstract of an integrated GCD with children of a preparatory group for school with general underdevelopment of speech on the topic: "Grapes"
Theme "Grapes".
Integration of educational areas: "Cognitive and research development", "Artistic and aesthetic development", "Social and communicative development".
Tasks:
1) Strengthening children's knowledge on the lexical topic "Fruits-Berries" ("Cognitive - research activities").
2) Development of fine motor skills and articulatory motor skills. The development of speech breathing and voice. "Communicative activity"
3) Improving the techniques of modeling from salt dough. ("Fine activity").
Methods and techniques:
- practical - modeling
- visual - a selection of illustrations depicting grapes, a model.
- verbal - a conversation about berries.
Materials and equipment: mirrors, pictures of a garden, replicas of grapes, colored salt dough, brushes, water plates, water, clipboards, stacks, raisins, grapes and grape juice.
Logic of educational activity
| No. | Educator activity.
| Children's activities. | Expected result. | ||
| 1 | Speech therapist and art teacher: "Hello children." | Children: "Hello" | Children's interest In the meantime, the one who has the sound “A” in the name at the beginning of the word (Galya, Olya, Nikita, Anya) will sit down” Speech therapist teacher: “Well done. And now the one who has the sound “A” in the second name sits down. | (Children's answers). | Expand knowledge about berries |
| 3 | Speech therapist: “Well done, how much you know fruits! Now let's talk about berries. Let's remember what berries do you know? (Children answer). Well done! And now take the mirrors in your hands and let's do the gymnastics for the tongue: Once - a little mouse yawned in the forest. Open mouth, stick out wide tongue, open your mouth wide and close it Two - kitten laps soup. Perform laxative movements with the tongue Three - the horse galloped. Keep your mouth wide open, smile; Open your mouth wide and smile. Stick the tongue to the palate and do not tear it off, pull the lower jaw down, stretching the hyoid ligament Five - chatting turkeys. Six - swing by the river. Open your mouth, stretch your tongue to the nose, then to the chin, do not close your mouth Seven - we will ask for jam. Open your mouth and smile, lick your upper lip with a wide tongue, while trying to “hug” your tongue immediately on the upper lip We will throw an eight-ball. Tongue between upper lip and teeth Nine - drumming loudly. Keep your mouth wide open. Tap the tongue on the inner surface of the upper incisors, pronouncing "d-d-d-d-d-d" Ten - we have a quiet rest. Mouth close. The tongue lies calmly in the mouth” | Children, together with a speech therapist teacher, perform exercises. | Change of mood and activity. | ||
| 4 | Speech therapist: “Well done. Deep breath, pause, noisy exhalation --- voice exercise: depict the howling of the autumn wind: UUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUingUUUUUUUUUUUUUUUinginging from strong wind for, softly from weak Wind." | Children together with a speech therapist teacher | |||
| 5 | Speech therapist teacher: “Well done! Sit down and let's continue Now I'm going to show you something (showing raisins). - Who knows what it is? Well done, raisins are right, but who knows what it comes from? - "Properly from grapes!" | Suggested responses from children. | To consolidate knowledge about grapes. | ||
| 6 | Speech therapist shows real grapes, models of green and black grapes are offered to children to study through tactile sensations. Look at the dummies, take the berries in your hands, what are they? | Children talk about their feelings. | Development of fine motor skills. Get ready for the next activity. | ||
| 7 | Art teacher: "Guys, now listen to an interesting legend about grapes." | ||||
| 8 | Speech therapist teacher: “Grapes appeared on our Earth a very, very long time ago. His parents were the earth and the sun. | Children listen attentively to the legend of grapes. | To form attention and perseverance. | ||
| 9 | Art teacher: “Now, in our time, grapes ripen for several months: the first ripens already in the middle of summer, and the last harvest is harvested in the middle of autumn. But the earth and the sun still remain the parents of grapes. Without the sun, neither a grain nor a berry can ripen. And the earth gives nourishment to the roots of the grape bush. " | ||||
| 8 | Speech therapist: “The stem and branches of grapes are called vines. What about grapes? The fact that it is rich in juice, The fact that its juice is magical, It is not simple, but healing!” | ||||
| 10 | Speech therapist teacher: “And one more delicious delicacy is given to us by grapes – raisins. Raisins are dried grapes. They are also very helpful. Grapes, juice and raisins cleanse the human body, give it strength and health.” | Good mood, for future activities | |||
| 11 | Art teacher: "Let's do a juice and raisin tasting." | Children taste raisins. | |||
| 12 | Speech therapist: “Now let’s rest a bit and do facial exercises You came to the garden and saw big apples like A (surprise) a lot of them! (joy) Picked an apple (depicting how we pick) Bit off and there is a worm! (fear, disappointment) Well done, sit down at the table.” | Children do exercises together with the teacher. | Change of activity and mood. | ||
| 13 | Art teacher: - “Guys, now we will look at the fake grapes again, you looked and tried raisins and grape juice, and now let's make a bunch of grapes from salt dough. - Remember the legend. What color will the grapes ripen according to the legend in the morning? | Children's answers: "Golden, yellow" . | Develop soldering. | ||
| 14 | - “And what color will the grapes that ripened according to the legend in the evening”?. | Children’s answers: “Dark blue, purple” | |||
| 15 dark blue, purple). – What does a bunch consist of? | Children's answers: "From individual berries" | ||||
| 16 | - "What do they look like?" | Children's answers: “Separate berries-balls are collected in a bunch” | |||
| 17 | - “Tear off a piece of dough and roll them into balls. - Are all the berries the same size or are they different? | Children's answers: "Berries can be of different sizes." | |||
| 18 | - "How can we collect berries so that they become like a bunch"? | Children answer: “We moisten individual berries with water with a brush and connect them together in a bunch.” | |||
| 19 | - “Note that the bunch of grapes is wider at the top than at the bottom, what does it mean”? | Children's answers: "There are more berries in the bunch from above." | |||
| 20 | The teacher shows how to mold a leaf from a piece of green dough. |

 He wrote fundamental works on the theory of dimension (which studies various, including very abstract, approaches to the concept of the dimension of space). He also studied other homological invariants of topological spaces. However, later the works of M.F. Bokshtein began to get closer to algebra, he was one of the few domestic mathematicians at that time who were engaged in homological algebra (closely related to topology), to which he was led by the study of the dimension of topological spaces with different groups of coefficients.
He wrote fundamental works on the theory of dimension (which studies various, including very abstract, approaches to the concept of the dimension of space). He also studied other homological invariants of topological spaces. However, later the works of M.F. Bokshtein began to get closer to algebra, he was one of the few domestic mathematicians at that time who were engaged in homological algebra (closely related to topology), to which he was led by the study of the dimension of topological spaces with different groups of coefficients.  Then, on the basis of this construction, he and other mathematicians also constructed Bockstein's cohomological operations - one of the important computational tools of modern topology (along with Steenrod operations, Massey products, etc.). The higher Bockstein cohomology operations on the cohomology group H*(X,Zp) of a topological space X with integer coefficients modulo a prime number p allow us to calculate the free part and the p-component of the integer cohomology group H*(X,Z).
Then, on the basis of this construction, he and other mathematicians also constructed Bockstein's cohomological operations - one of the important computational tools of modern topology (along with Steenrod operations, Massey products, etc.). The higher Bockstein cohomology operations on the cohomology group H*(X,Zp) of a topological space X with integer coefficients modulo a prime number p allow us to calculate the free part and the p-component of the integer cohomology group H*(X,Z). 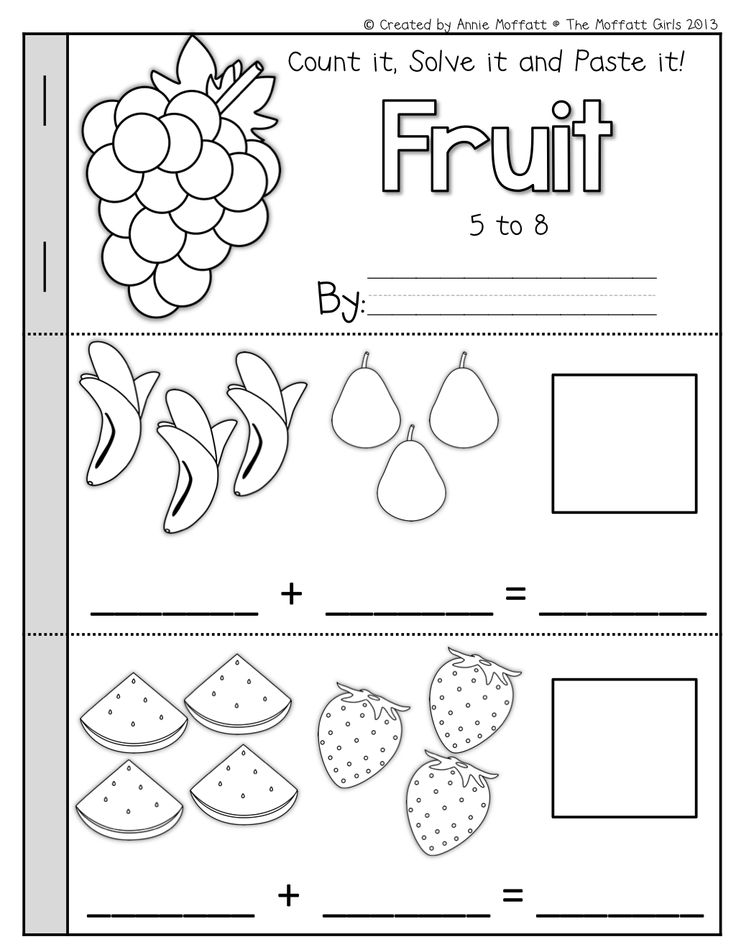
 e. provided that the argument (usually identified with time) increases indefinitely. This kind of research makes it possible to determine what will happen to the object described by differential equations after a sufficiently long period of time. An exact, analytical solution of even the simplest linear systems can be obtained very rarely (a welcome exception is systems of linear differential equations with constant coefficients, where the theory and methods of solution can be considered completely completed). Therefore, any, even purely qualitative information (such as the nature of the behavior of solutions at infinity) turns out to be extremely useful. It is of considerable interest to isolate solutions that are stable at infinity. Stability can be understood in several different senses, usually stability is understood as Lyapunov stability (introduced and studied in detail by the Russian mathematician A.M. Lyapunov at the turn of 19th and 20th centuries) and its modifications (in particular, asymptotic stability and exponential stability).
e. provided that the argument (usually identified with time) increases indefinitely. This kind of research makes it possible to determine what will happen to the object described by differential equations after a sufficiently long period of time. An exact, analytical solution of even the simplest linear systems can be obtained very rarely (a welcome exception is systems of linear differential equations with constant coefficients, where the theory and methods of solution can be considered completely completed). Therefore, any, even purely qualitative information (such as the nature of the behavior of solutions at infinity) turns out to be extremely useful. It is of considerable interest to isolate solutions that are stable at infinity. Stability can be understood in several different senses, usually stability is understood as Lyapunov stability (introduced and studied in detail by the Russian mathematician A.M. Lyapunov at the turn of 19th and 20th centuries) and its modifications (in particular, asymptotic stability and exponential stability). In addition, they study Lagrange stability, Poisson stability, structural stability (introduced by A.A. Andronov and L.S. Pontryagin), etc.
In addition, they study Lagrange stability, Poisson stability, structural stability (introduced by A.A. Andronov and L.S. Pontryagin), etc.  More precisely, the characteristic index lx(t) is the upper limit of the ratio ln|x(t)|/t at t®Ґ. Choosing a normal fundamental system of solutions to a system of linear differential equations and calculating the corresponding characteristic exponents for them, we obtain the spectrum of the system. The largest of these indicators is denoted by l1 and is called the senior characteristic indicator of the system. So, it is with the value of this senior indicator that the answer to the question about the stability of the system is connected in the first Lyapunov method. Namely, if this number is negative, then all solutions of the system are asymptotically stable, and if it is positive, then they are unstable. If a linear system is obtained by linearizing a nonlinear one, then, unfortunately, it does not necessarily follow from the asymptotic stability of solutions of this linear system that the original system has the same property. However, this is still true for regular (selected by the condition of convergence of some improper integral composed of the coefficients of the original linear system) linear systems (Lyapunov's theorem).
More precisely, the characteristic index lx(t) is the upper limit of the ratio ln|x(t)|/t at t®Ґ. Choosing a normal fundamental system of solutions to a system of linear differential equations and calculating the corresponding characteristic exponents for them, we obtain the spectrum of the system. The largest of these indicators is denoted by l1 and is called the senior characteristic indicator of the system. So, it is with the value of this senior indicator that the answer to the question about the stability of the system is connected in the first Lyapunov method. Namely, if this number is negative, then all solutions of the system are asymptotically stable, and if it is positive, then they are unstable. If a linear system is obtained by linearizing a nonlinear one, then, unfortunately, it does not necessarily follow from the asymptotic stability of solutions of this linear system that the original system has the same property. However, this is still true for regular (selected by the condition of convergence of some improper integral composed of the coefficients of the original linear system) linear systems (Lyapunov's theorem).
 F. Bylov) R.E. Vinograd published in 1966 the monograph "Theory of Lyapunov exponents and its applications to questions of stability theory". This book was very popular both in the USSR and abroad, among mathematicians and specialists in other sciences who apply the theory of differential equations (mechanics, physics, control theory, etc.).
F. Bylov) R.E. Vinograd published in 1966 the monograph "Theory of Lyapunov exponents and its applications to questions of stability theory". This book was very popular both in the USSR and abroad, among mathematicians and specialists in other sciences who apply the theory of differential equations (mechanics, physics, control theory, etc.).  For many years this book was practically the only "elementary" exposition of higher mathematics in the USSR. It was studied not only in technical schools, it was used for the first acquaintance with higher mathematics and many future mathematicians when they were schoolchildren. N.P. Tarasov actively translated educational literature into Russian, he himself participated in the preparation of textbooks. During the work of N.P. Tarasov at MATI, the department carried out active methodological work, developed and published course programs and methodological manuals, which teachers and students used with pleasure many years later. In those days, many graduates of pedagogical universities worked at the department, who contributed to the high-quality formulation of the pedagogical process and methodological work.
For many years this book was practically the only "elementary" exposition of higher mathematics in the USSR. It was studied not only in technical schools, it was used for the first acquaintance with higher mathematics and many future mathematicians when they were schoolchildren. N.P. Tarasov actively translated educational literature into Russian, he himself participated in the preparation of textbooks. During the work of N.P. Tarasov at MATI, the department carried out active methodological work, developed and published course programs and methodological manuals, which teachers and students used with pleasure many years later. In those days, many graduates of pedagogical universities worked at the department, who contributed to the high-quality formulation of the pedagogical process and methodological work.  Bauman in 1956, defended his Ph.D. thesis in 1961 and became a Doctor of Technical Sciences in 1964. V.F. Krotov was engaged in the theory of optimal control. His first work was published in 1960 and dealt with discontinuous solutions to variational problems. Many of his papers were devoted to sufficient extremum conditions - they are especially valued in applied areas, in contrast to simpler necessary conditions. At that time, Vladimir Iosifovich Gurman, another well-known specialist in the theory of optimal control, also worked at the department. V.F. Krotov together with V.I. Gurman and another teacher of the department - V.Z. Bukreev at 19In 1969 he published a monograph "New Methods of the Calculus of Variations in Flight Dynamics" devoted to calculations of the motion of aircraft. At that time, on the basis of the Department of Higher Mathematics of the MATI, an inter-institutional scientific seminar on optimal control was operating, at which well-known experts in this and related fields of mathematics, as well as novice mathematicians who gained fame in subsequent years, made presentations.
Bauman in 1956, defended his Ph.D. thesis in 1961 and became a Doctor of Technical Sciences in 1964. V.F. Krotov was engaged in the theory of optimal control. His first work was published in 1960 and dealt with discontinuous solutions to variational problems. Many of his papers were devoted to sufficient extremum conditions - they are especially valued in applied areas, in contrast to simpler necessary conditions. At that time, Vladimir Iosifovich Gurman, another well-known specialist in the theory of optimal control, also worked at the department. V.F. Krotov together with V.I. Gurman and another teacher of the department - V.Z. Bukreev at 19In 1969 he published a monograph "New Methods of the Calculus of Variations in Flight Dynamics" devoted to calculations of the motion of aircraft. At that time, on the basis of the Department of Higher Mathematics of the MATI, an inter-institutional scientific seminar on optimal control was operating, at which well-known experts in this and related fields of mathematics, as well as novice mathematicians who gained fame in subsequent years, made presentations. Then the foundations of the theory of degenerate problems for unbounded differential inclusions and optimal control for hybrid (discrete-continuous) systems (V.I. Gurman), new computational methods (V.F. Krotov, V.I. Gurman) were laid, and sufficient conditions were obtained invariance of controlled systems (M.M. Khrustalev). On this basis, a number of major applied studies have been carried out, such as optimization of orientation maneuvers of spacecraft (V.I. Gurman, A.M. Nikulin), optimization of helicopter takeoffs with a unique result - a reduction in takeoff distance by 40-50% (Gurman V.I. ., Chuklov B.T.) and others, incl. under contracts with leading aerospace organizations. With firms S.P. Koroleva, M.K. Yangel, V.N. Chelomeya, A.S. Lavochkina, TsNIIMash and others concluded economic contracts for the implementation of research to find optimal modes and laws for controlling space objects that were being prepared for launch at these enterprises. Much attention was paid to the scientific work of teachers.
Then the foundations of the theory of degenerate problems for unbounded differential inclusions and optimal control for hybrid (discrete-continuous) systems (V.I. Gurman), new computational methods (V.F. Krotov, V.I. Gurman) were laid, and sufficient conditions were obtained invariance of controlled systems (M.M. Khrustalev). On this basis, a number of major applied studies have been carried out, such as optimization of orientation maneuvers of spacecraft (V.I. Gurman, A.M. Nikulin), optimization of helicopter takeoffs with a unique result - a reduction in takeoff distance by 40-50% (Gurman V.I. ., Chuklov B.T.) and others, incl. under contracts with leading aerospace organizations. With firms S.P. Koroleva, M.K. Yangel, V.N. Chelomeya, A.S. Lavochkina, TsNIIMash and others concluded economic contracts for the implementation of research to find optimal modes and laws for controlling space objects that were being prepared for launch at these enterprises. Much attention was paid to the scientific work of teachers. Employees of the department took an active part in all all-Union meetings on astronautics, made presentations at the Readings of K.E. Tsiolkovsky, Yu.A. Gagarin, F.A. Zander, international congresses on automatic control, mechanics, aviation and astronautics.
Employees of the department took an active part in all all-Union meetings on astronautics, made presentations at the Readings of K.E. Tsiolkovsky, Yu.A. Gagarin, F.A. Zander, international congresses on automatic control, mechanics, aviation and astronautics.  Some of them continue to work at MATI until now, two defended their doctoral dissertations - Gorbatsevich V.V. (at 1983) and the current head of the department Osipenko K.Yu. (in 1994). Much attention was paid to the development of computer technology. It was at that time that a computer center was created at the MATI at the Department of Higher Mathematics and the active use of computers in the educational and scientific work of the departments of the institute began. The range of applied research has expanded, a lot of methodological literature has been published. At that time, the course of higher mathematics as a whole underwent a radical restructuring, approaching the requirements of the current state of engineering science.
Some of them continue to work at MATI until now, two defended their doctoral dissertations - Gorbatsevich V.V. (at 1983) and the current head of the department Osipenko K.Yu. (in 1994). Much attention was paid to the development of computer technology. It was at that time that a computer center was created at the MATI at the Department of Higher Mathematics and the active use of computers in the educational and scientific work of the departments of the institute began. The range of applied research has expanded, a lot of methodological literature has been published. At that time, the course of higher mathematics as a whole underwent a radical restructuring, approaching the requirements of the current state of engineering science.  A display class based on the ES-1033 computer was created at the department. The department took an active part in the beginning process of computerization of the Institute. In the display class, teachers and senior staff of the institute were taught the basics of working with computers.
A display class based on the ES-1033 computer was created at the department. The department took an active part in the beginning process of computerization of the Institute. In the display class, teachers and senior staff of the institute were taught the basics of working with computers. 
 His name is included in the famous international reference books "Who's Who in the World", "Who's Who in Science and Engineering", "2000 Outstanding Intellectuals of the 20th Century" and others. In 2000, K.Yu. Osipenko received the honorary title of Soros Professor.
His name is included in the famous international reference books "Who's Who in the World", "Who's Who in Science and Engineering", "2000 Outstanding Intellectuals of the 20th Century" and others. In 2000, K.Yu. Osipenko received the honorary title of Soros Professor. 
 By order of the departments "Physics", "Testing of aircraft", the Higher School of Environmental Engineering, etc., many new programs were prepared, which were the result of the active work of the methodological commission of the department.
By order of the departments "Physics", "Testing of aircraft", the Higher School of Environmental Engineering, etc., many new programs were prepared, which were the result of the active work of the methodological commission of the department.  chat.ru/~mati_vm), the number of visitors to which is now approaching 3,200. On this page, in addition to detailed information about the teachers and staff of the department, programs , schedules of consultations, collected almost all methodological manuals of the department, released in recent years. The department page is also available in the display classes in the so-called "offline" mode (without Internet access), so the teaching aids issued by the department are easily accessible to every student. The same page provides detailed information about the scientific work of the department and the scientific works published by its teachers.
chat.ru/~mati_vm), the number of visitors to which is now approaching 3,200. On this page, in addition to detailed information about the teachers and staff of the department, programs , schedules of consultations, collected almost all methodological manuals of the department, released in recent years. The department page is also available in the display classes in the so-called "offline" mode (without Internet access), so the teaching aids issued by the department are easily accessible to every student. The same page provides detailed information about the scientific work of the department and the scientific works published by its teachers.  Leading professors of the department often make presentations at the seminar on the current state of mathematics in areas close to their professional interests.
Leading professors of the department often make presentations at the seminar on the current state of mathematics in areas close to their professional interests. 
 Well done, and now the one who has the sound "A" at the end of the name sits down. Well done, everyone sit down! Today we will remember where fruits grow and what kind you know "
Well done, and now the one who has the sound "A" at the end of the name sits down. Well done, everyone sit down! Today we will remember where fruits grow and what kind you know " Open your mouth wide, “talk” with your tongue, moving it back and forth along the upper lip: “bl-bl-bl-bl-bl-bl. "
Open your mouth wide, “talk” with your tongue, moving it back and forth along the upper lip: “bl-bl-bl-bl-bl-bl. "  And now we get up and breathe a little: (setting lower diaphragmatic breathing). The exercise is performed while standing, hand on the diaphragm:
And now we get up and breathe a little: (setting lower diaphragmatic breathing). The exercise is performed while standing, hand on the diaphragm: 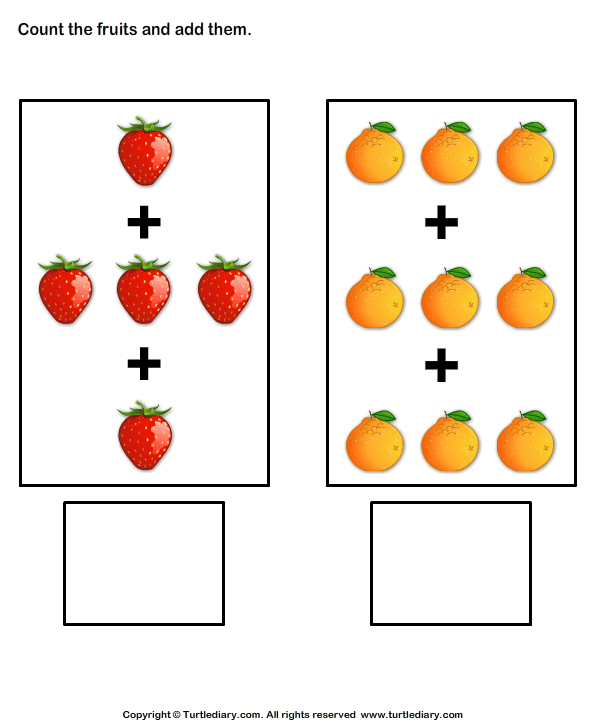
 In those days, grapes did not ripen for a month, not two, as now, but quickly - from morning to evening. And those grapes that had time to ripen at dawn, became golden (from the sun, and ripened late in the evening, became dark or velvety blue grapes "
In those days, grapes did not ripen for a month, not two, as now, but quickly - from morning to evening. And those grapes that had time to ripen at dawn, became golden (from the sun, and ripened late in the evening, became dark or velvety blue grapes " Repeat this word and try to remember it. The vine is very flexible and thin, so it must be tied to a post. Grapes make a very tasty and healthy juice.
Repeat this word and try to remember it. The vine is very flexible and thin, so it must be tied to a post. Grapes make a very tasty and healthy juice. 

 How do they look?
How do they look?