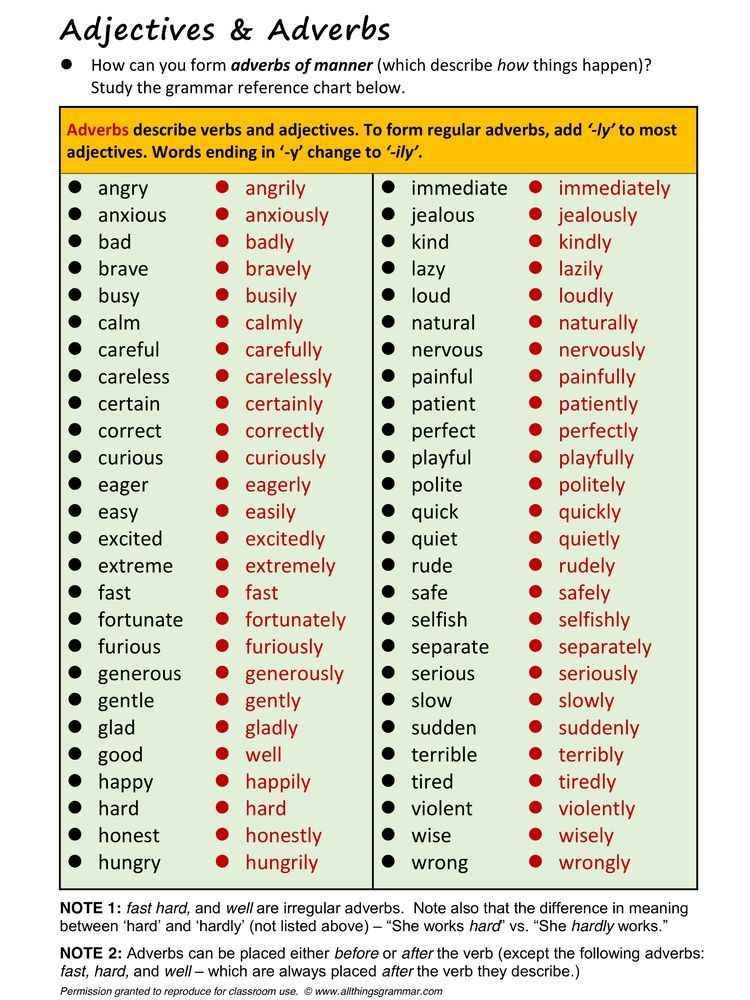
Understand math concepts
Understanding Mathematics
Understanding MathematicsPeter Alfeld, --- Department of Mathematics, --- College of Science --- University of Utah
a study guide by Peter Alfeld.
I wrote this page for students at the University of Utah. You may find it useful whoever you are, and you are welcome to use it, but I'm going to assume that you are such a student (probably an undergraduate), and I'll sometimes pretend I'm talking to you while you are taking a class from me.
Let's start by me asking you some questions. If you are interested in some suggestions, comments, and elaborations, click on the Comments. Do so in particular if you answered "Yes!". (In making the comments I assume you did say "Yes!", so don't be offended if you didn't and are just curious.)
- Do you feel
- That being lost in mathematics is the natural state of things? Comments.
- That lectures and textbooks are incomprehensible? Comments.
- That the amount of material in any math course is so overwhelming that you (or anybody else) could not possibly absorb it? Comments.

- That mathematics is just a collection of formulas and theorems that one somehow has to cram into one's head? Comments.
- That the solution of problems requires a collection of tricks whose conception was based on a generous allowance of magic? Comments.
- That math courses are just hurdles one has to cross as an undergraduate student? Comments.
- That mathematics is irrelevant? Comments.

- Are you taking mathematics only because it's required? Comments.
- Are you frustrated working through heaps of meaningless problems that are all alike? Comments.
- Does the thought "I can look it up if I have to " occur to you frequently? Comments.
- When solving assigned problems, do you often think "What does he want us to do?"? Comments.
- Do you find yourself frequently searching through literature in vague hopes of finding a helpful formula or theorem? Comments.

- Do the proofs you find in your textbook or in the literature look contrived to you? Comments.
- Do you often wonder why your teachers make you study a piece of mathematics that could not possibly ever be useful? Comments.
- Are you upset that the teacher insists on doing proofs rather than telling you how to solve problems? Comments. >
- Do you often wish your teacher would do more examples? Comments.
- When you are trying to solve a problem, do you find yourself frequently spinning your wheels, hoping for an idea that never comes? Comments.

- Do you ask questions in class? Comments.
- Do you sell your textbook after you take a math class? Comments.
- Do you find it difficult to prepare for an exam? Comments.
- Do you worry about your grade a lot? Comments.
- Do you skip class a lot? Comments.
- Do you often leave class early? Comments.
- Do you often repeat courses? Comments.
- Do you cheat on exams? Comments.
If your answer to all of these questions is a resounding "No!" then you should read no further and return to the study of mathematics. I'd also like to meet you, please drop me an e-mail! Otherwise I'm hoping that this page has something to offer you (and of course you may send me an e-mail anyway). I believe that many students struggle with mathematics only because they don't know what it means to understand Mathematics and how to acquire that understanding.
The purpose of this page is to help you learn how to approach mathematics in a more effective way.
Understanding Mathematics
You understand a piece of mathematics if you can do all of the following:- Explain mathematical concepts and facts in terms of simpler concepts and facts.
- Easily make logical connections between different facts and concepts.
- Recognize the connection when you encounter something new (inside or outside of mathematics) that's close to the mathematics you understand.
- Identify the principles in the given piece of mathematics that make everything work. (i.e., you can see past the clutter.)
By contrast, understanding mathematics does not mean to memorize Recipes, Formulas, Definitions, or Theorems.
Clearly there must be some starting point for explaining concepts in terms of simpler concepts. That observation leads to deep and arcane mathematical and philosophical questions and some people make it their life's work to think about these matters. For our purposes it suffices to think of elementary school math as the starting point. It is sufficiently rich and intuitive.
For our purposes it suffices to think of elementary school math as the starting point. It is sufficiently rich and intuitive.
All of this is neatly summarized in a letter that Isaac Newton wrote to Nathaniel Hawes on 25 May 1694.
People wrote differently in those days, obviously the " vulgar mechanick" may be a man and "he that is able to reason nimbly and judiciously" may be a woman, (and either or both may be children).
Here's anExample: Powers
for complicated mathematics building on simpler mathematics.
The following examples illustrate the difference between the two approaches to understanding mathematics described above.
Example: Conversion of logarithms.
Example: Solving a quadratic equation.
You won't be able to learn how to understand mathematics from abstract principles and a few examples. Instead you need to study the substance of mathematics. I'm hoping that the answers to the following
Frequently Asked Questions
will illustrate how mathematics is meant to make sense and is built on a logical procession rather than a bunch of arbitrarily conceived rules.
One of the main things that turned me on to mathematics were certain concepts and arguments that I found particularly beautiful and intriguing. I'm listing some of these below even though they may not be frequently asked about. But I'll hope you'll enjoy them, and perhaps get more interested in mathematics for its own sake.
But I'll hope you'll enjoy them, and perhaps get more interested in mathematics for its own sake.
Mathematical Gems
Solving Mathematical Problems
The most important thing to realize when solving difficult mathematical problems is that one never solves such a problem on the first attempt. Rather one needs to build a sequence of problems that lead up to the problem of interest, and solve each of them. At each step experience is gained that's necessary or useful for the solution of the next problem. Other only loosely related problems may have to be solved, to generate experience and insight.
Students (and scholars too) often neglect to check their answers. I suspect a major reason is that traditional and widely used teaching methods require the solution of many similar problems, each of which becomes a chore to be gotten over with rather than an exciting learning opportunity. In my opinion, each problem should be different and add a new insight and experience. However, it is amazing just how easy it is to make mistakes. So it is imperative that all answers be checked for plausibility. Just how to do that depends of course on the problem.
In my opinion, each problem should be different and add a new insight and experience. However, it is amazing just how easy it is to make mistakes. So it is imperative that all answers be checked for plausibility. Just how to do that depends of course on the problem.
There is a famous book: G. Polya, "How to Solve It ", 2nd ed., Princeton University Press, 1957, ISBN 0-691-08097-6. It was first published in 1945. This is a serious attempt by a master at transferring problem solving techniques. Click here to see an html version of Polya's summary.
Acquiring Mathematical Understanding
Since this is directed to undergraduate students a more specific question is how does one acquire mathematical understanding by taking classes? But that does not mean that classes are the only way to learn something. In fact, they often are a bad way! You learn by doing. For example, it's questionable that we should have programming classes at all, most people learn programming much more quickly and enjoyably by picking a programming problem they are interested in and care about, and solving it. In particular, when you are no longer a student you will have acquired the skills necessary to learn anything you like by reading and communicating with peers and experts. That's a much more exciting way to learn than taking classes!
In fact, they often are a bad way! You learn by doing. For example, it's questionable that we should have programming classes at all, most people learn programming much more quickly and enjoyably by picking a programming problem they are interested in and care about, and solving it. In particular, when you are no longer a student you will have acquired the skills necessary to learn anything you like by reading and communicating with peers and experts. That's a much more exciting way to learn than taking classes!
Here are some suggestions regarding class work:
- Always strive for understanding as opposed to memorization.
- If this means you have to go back, do it! Don't postpone clarifying a point you miss because everything new will build on it.
- It may be intimidating to be faced with a 1,000 page book and having to spend a day understanding a single page. But that does not mean that you'll have to spend a thousand days understanding the whole book. In understanding that one page you'll gain experience that makes the next page easier, and that process feeds on itself.
- Read the sections covered in class before you come to class. That's one of the most useful ways in which you can spend your time, because it will dramatically increase the effectiveness of the lecture.
- Do exercises. The teacher may suggest some, put you can pick them on your own from the textbook or make up your own. Select them by the amount of interest they hold for you and the degree of curiosity they stimulate in you.
 Avoid getting into a mode where you do a large number of exercises that are distinguished only by the numerical values assigned to some parameters.
Avoid getting into a mode where you do a large number of exercises that are distinguished only by the numerical values assigned to some parameters. - Always check your answers for plausibility.
- Whenever you do a problem or follow a new mathematical thread explicitly formulate expectations. Your expectations may be met, which causes a nice warm feeling (and you should probably also look for a new and different problem). But otherwise there are two possibilities: you made a mistake from which you can recover, now that you are aware of it, or there is something genuinely new that you can figure out and which will teach you something. If you don't formulate and check expectations you may miss these opportunities.
- Find a class mate who will work with you in a team. Have one of you explain the material to the other, on a regular basis, or switch periodically. Explaining math to others is one of the best ways of learning it.
- Be open and alert to the use of new technology. (I know you are because you are reading this web page.) You can go from here directly to computing help. But don't neglect thinking about the problem and understanding it, its solution, and its ramifications. The purposes of technology are not to relieve you of the need to think but:
- To check your answers.
- To take care of routine tasks efficiently.

- To do things that can't possibly be done by hand (like the visualization of large data sets).
- Once you are done with a course Keep Your Textbook and refer back to it when you need to. You have spent so much time with that book that you know it intimately and know how to use it and where to find the information you need. The small amount of money you might get by selling it does not come close to offsetting the loss in time and energy you waste being thwarted by a lack of understanding a particular piece of mathematics that you easily refamiliarize yourself with by consulting your old friend, the textbook.
 Here's a more passionate elaboration on this theme.
Here's a more passionate elaboration on this theme.
The Greatest Book on the Planet
My favorite of all books I have ever read, or otherwise examined, is "What is Mathematics" by Courant and Robbins. This book first appeared in 1943, and it is still in print! It is available as an inexpensive paperback: What Is Mathematics? An Elementary Approach to Ideas and Methods by Richard Courant and Herbert Robbins, and updated in 1996 by Ian Stewart. Don't be mislead by the term "elementary". The book does start at the beginning, but it covers a huge swath of mathematics, and is suitable for many years of reading and careful study. It is intended to describe the spirit and contents of mathematics to the serious and curious, but perhaps uninitiated, and it is as close to being perfect as a book can be. Oxford University Press, USA; 2 edition (July 18, 1996), ISBN-10: 0195105192 and ISBN-13: 978-0195105193.
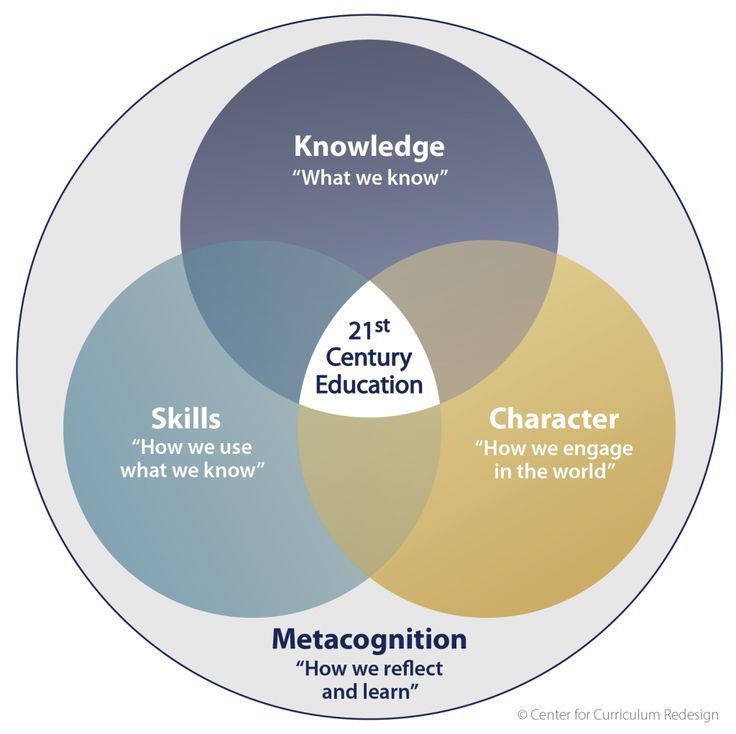
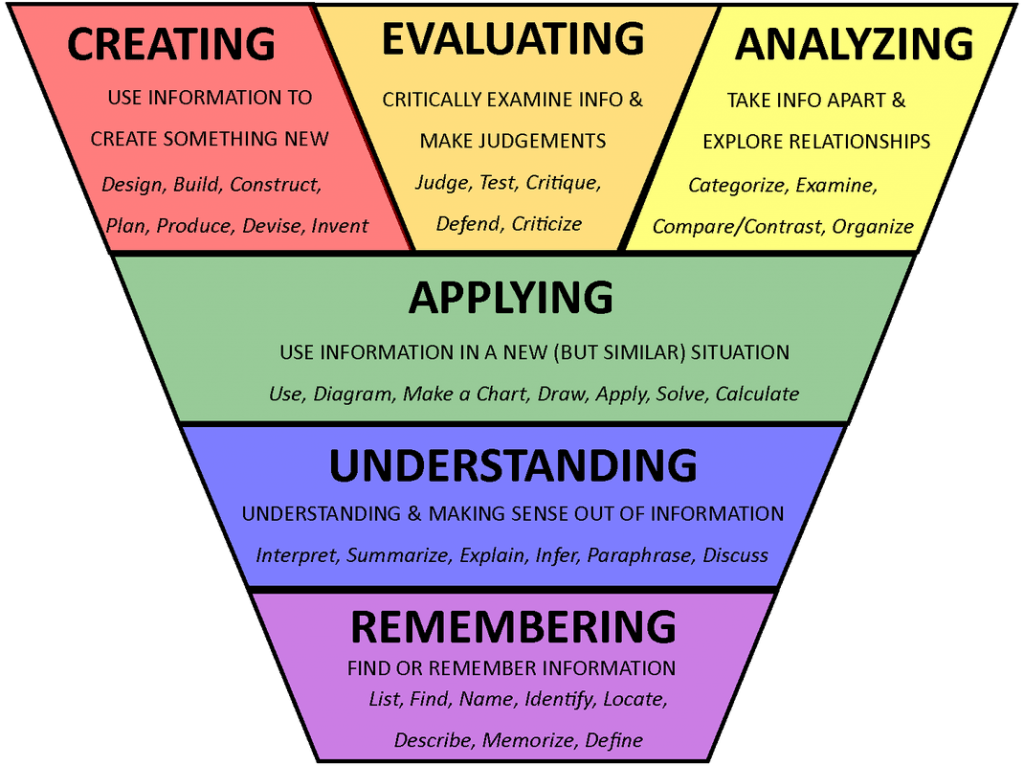
How to Guide Elementary Students to a Deep Understanding of Math Concepts
When we are passionate about a topic, or even a hobby, we tend to explore it in as many ways as possible. We might read books or blogs to learn facts, test emerging ideas on paper, and keep notes or ideas in our head until we can talk about the subject as experts.
Children learn very effectively using that same process. Teachers capitalize on this in the classroom, or perhaps these days over Zoom, by using a step-by-step strategy called CPA (concrete, pictorial, abstract) so that students can move from doing (concrete) to seeing (pictorial) to symbolic (abstract). These three building blocks are particularly important in math instruction.
When leading teacher professional development, I like to compare the strategy of moving students from concrete to pictorial to abstract to learning how to drive a car. Once you’re actually driving the car, you’re already in the abstract phase. But how do you reach that point?
First, you must know physically what a car is and what it does. You sit in it and learn about the ignition, the steering wheel, and other key parts, and what they do. Then, you enter the representational phase, in which you envision the steps needed to drive. Maybe you have a progression in your mind’s eye (pictorial) of everything that needs to be done: adjust the seat and mirrors, put on your seat belt, put your foot on the brake, shift into drive, and so on. Finally, after practice, you arrive at the stage where driving becomes so automatic (abstract) that you don’t even think about the checklist of steps.
You sit in it and learn about the ignition, the steering wheel, and other key parts, and what they do. Then, you enter the representational phase, in which you envision the steps needed to drive. Maybe you have a progression in your mind’s eye (pictorial) of everything that needs to be done: adjust the seat and mirrors, put on your seat belt, put your foot on the brake, shift into drive, and so on. Finally, after practice, you arrive at the stage where driving becomes so automatic (abstract) that you don’t even think about the checklist of steps.
The goal of using the CPA building blocks is to reach the abstract phase with an understanding that enables flexibility and proficiency in problem solving. A student should ultimately be able to work in the abstract, picking and choosing the facts and tools needed in a particular situation. I’ve found over the years that this strategy improves overall problem-solving abilities in students. They become adept at transferring the skills learned and applying them to new situations.
The CPA Progression in Early Learning
For children in pre-K or kindergarten, seeing different arrangements of five objects, like buttons or blocks, and counting them to make five (the concrete) helps prepare the students to learn basic math facts. They explore relationships, test ideas, and make connections. Building those foundations of knowledge is key to becoming fluent in computation without always having to rely on a calculator later.
Being able to illustrate the physical objects in a drawn or written model (the pictorial) clarifies ideas, expands perspectives, and opens doors to different approaches to problem-solving. Children learn to translate the objects they see and can touch into a picture by drawing tally marks, dots, or a diagram.
The mathematical representation might also be presented in words to help the student clarify thoughts. So, a student might write a sentence, or the teacher might present the student with a prompting sentence such as, “An arrangement of two dots and three dots is five dots. ”
”
Finally, the most challenging area of learning is moving to the abstract phase. For very young children, this might be recognizing that an arrangement of objects is five without having to count the pieces.
The CPA Progression in Upper Elementary and Middle Grades
Older elementary and middle grade children benefit from the CPA process as well, as they continue to absorb the abstract. For instance, the idea of adding “like objects” may seem very simple with whole-number computation, but a solid grasp of the concept becomes a critical framework for tackling more advanced material in upper grades, including calculations with rational numbers (fractions) or unknowns (variables).
For example, if students have a thorough understanding of how like quantities are combined, such as in “2 + 3 = 5,” they can tackle increasingly complex problems rooted in these ideas with much more ease. Some examples:
- 2 apples + 3 apples adds up to 5 apples.
- 2 sixths and 3 sixths equals 5 sixths, or 2/6 + 3/6 = 5/6.

- 2 like unknowns and 3 like unknowns is 5 like unknowns, or 2x + 3x = 5x.
These last two examples appear in math curricula from upper elementary through algebra and are common stumbling—or building—blocks for students. When students struggle with how to add variables in algebra, they may have missed a connection necessary to go the entire way from concrete to abstract. In this case, objects that are alike may be combined, no matter how intangible the objects are. Just as apples and apples are alike, x’s and x’s are alike and may be added.
Principles to Guide You as You Use CPA Building Blocks With Your Students
Parents who didn’t learn this way might ask, “Why go through all that trouble? It takes so much time, and do you really need buttons or blocks in math class?” You might explain CPA to parents this way: It’s like having training wheels before learning how to ride a regular two-wheeler. It helps you get started and can save time later by growing understanding now. With math, you may be able to go straight to abstract thinking, but it’s helpful to have a fallback to reconstruct the process in case you forget the equation or need to apply the idea to a new or more complex problem.
With math, you may be able to go straight to abstract thinking, but it’s helpful to have a fallback to reconstruct the process in case you forget the equation or need to apply the idea to a new or more complex problem.
Also, learning isn’t always linear. Some young children may get to the pictorial phase quickly or understand a concept in an abstract way when a topic is first introduced. But that’s not the point of entry for most children, and if a child is confused later, it may be necessary to revisit an earlier step.
Remember as well that symbols, equations, and even mathematical terms can be a mystery when students first encounter them, to the point where they can look like a foreign language. Building from concrete to pictorial to abstract gives students a process to crack the code and understand the “language” used.
Finally, CPA is natural scaffolding. It’s important that students connect the three phases and see them as linked, as opposed to perceiving them as three separate and unrelated steps. Teachers can give prompts and lead students to make connections if they are not getting it on their own. When a student struggles with a concept in later grades, teachers can frequently trace that gap to the learning development in earlier grades when the concrete or pictorial areas were skipped or perhaps not connected. Teachers can sometimes address the problem by returning to a more foundational level and making intentional connections between phases.
Teachers can give prompts and lead students to make connections if they are not getting it on their own. When a student struggles with a concept in later grades, teachers can frequently trace that gap to the learning development in earlier grades when the concrete or pictorial areas were skipped or perhaps not connected. Teachers can sometimes address the problem by returning to a more foundational level and making intentional connections between phases.
Whether you’re shifting your teaching practice or being more intentional about a strategy you already use, leveraging the CPA building blocks as a core instructional approach will have lasting benefits for you and your students.
Topic 7. Mathematical concepts Content
-
Mathematical concepts. The scope and content of the concept.
-
Relationship genus and species between concepts.
-
Definition concepts.
-
Requirements to the definition of concepts.

five. Implicit definitions
Main literature 7, 14, 16, 24, 25, 30, 33, 34;
Additional literature 26, 44
studying mathematics at school, college, university, need to learn a certain system concepts, propositions and proofs, but to master this system and then successfully apply acquired knowledge and skills, teaching younger students and solving the problem of their development by means mathematics, one must first understand what features of mathematical concepts, how their definitions, sentences, expressing properties of concepts, and evidence.
Any mathematical object has certain properties. For example, a square has four sides right angles equal to diagonals. Can specify other properties of the square. nine0005
Among properties of an object distinguish between properties essential and minor to distinguish it from other objects. Property consider significant for object, if it is inherent in this object and without it it cannot exist. Insignificant properties are those properties, the absence of which does not affect the existence of the object. So, for example, the named properties of a square are essential, and the property "side AB of the square is vertical" insignificant. If the square is turned then side AB will be located differently (Fig. 1). nine0005
Property consider significant for object, if it is inherent in this object and without it it cannot exist. Insignificant properties are those properties, the absence of which does not affect the existence of the object. So, for example, the named properties of a square are essential, and the property "side AB of the square is vertical" insignificant. If the square is turned then side AB will be located differently (Fig. 1). nine0005
AT
AT C
AND C
AND D
D Rice. 1
That's why, to understand what is given mathematical object is enough know its essential properties. In that case, it is said that there is a concept of this object. nine0005
nine0005
When talk about a mathematical object, then usually mean the whole objects designated by one term, word, name. So when talking about square, then they mean all geometric shapes that are squares. Aggregate of all squares is the scope of the concept square.
Definition. The scope of a concept is the totality of all objects designated by the same term.
Any concept has not only scope, but also content. nine0005
Definition . The content of the concept is a set all essential properties of the object, reflected in this concept.
T. Well, every concept is characterized by term, volume, content.
Note. Between the scope of a concept and its content there is a connection: the "larger" volume concept, the "less" its content, and vice versa.
Example
Volume concept of "right triangle" "less than" the scope of the concept of "triangle", since the scope of the first concept includes not all triangles, but only rectangular ones. But the content of the first concept of "more" second content: rectangular the triangle possesses not only all properties of a triangle, but also others, inherent only to rectangular triangles.
But the content of the first concept of "more" second content: rectangular the triangle possesses not only all properties of a triangle, but also others, inherent only to rectangular triangles.
Any the concept cannot be grasped without realizing it relationships with other concepts. That's why it is important to know in what respects to be concepts, and to be able to establish these connections. nine0005
Relationship between concepts are closely related to relations between their volumes, i.e. sets.
Let's agree concepts are capitalized Latin alphabet: a, b, c, ..., z.
How to Invent a Mathematical Concept
If math is not good for you, it may not be about you, but how it is presented to you. Jason Wilks in his book Math on Fire. Non-boring non-textbook" turns the usual idea of mathematics as a boring and abstract discipline that only remains to memorize, and invites you to invent your own mathematics.
 Yes, yes, you read that right - invent. nine0115
Yes, yes, you read that right - invent. nine0115
Jason Wilkes
Mann, Ivanov & Ferber, 2020
Before we create an analysis, we need to learn how to create things. More precisely, we need to understand how to develop mathematical concepts. Let's illustrate the process with two simple examples: the area of a rectangle and the steepness of a line. We will see later that these two concepts form the backbone of the analysis. The first is the basis for the "integral", the second is for the "derivative". These concepts are opposite, and the exact meaning in which they are opposite is described by the so-called fundamental theorem of analysis (the Newton-Leibniz formula). nine0123
Don't worry if you already know how to calculate them. Anyone will gain something from discussing these issues - either in their understanding or in teaching them, since the process of invention is rarely discussed.
When we invent mathematics from scratch, we always start with an intuitively clear everyday concept. This process is not as mysterious as it seems. Creation is just a transition from qualitative to quantitative  The invention process contains an attempt to translate a fuzzy qualitative idea into a precise quantitative one. No one can truly represent an object in five, seventeen, or an infinite number of dimensions. How are mathematicians going to define something like "curvature" in a way that allows them to talk about the curvature of high-dimensional objects? How did a person come to the necessary definitions, when they are often so abstract that one seems to need to have superhuman abilities for multidimensional intuition in order to “see” the truth? nine0005
The invention process contains an attempt to translate a fuzzy qualitative idea into a precise quantitative one. No one can truly represent an object in five, seventeen, or an infinite number of dimensions. How are mathematicians going to define something like "curvature" in a way that allows them to talk about the curvature of high-dimensional objects? How did a person come to the necessary definitions, when they are often so abstract that one seems to need to have superhuman abilities for multidimensional intuition in order to “see” the truth? nine0005
I hope that explicit teaching of the process of creation at all levels of mathematics will one day find its rightful place in the curriculum, along with less important issues like addition, multiplication, lines, planes, circles, logarithms, groups Syulov, fractals and chaos, […] and everything else that we teach mathematics students from elementary school to doctoral studies. nine0023 But this is much more important than .
nine0023 But this is much more important than .
Mining in our brains: the invention of the area
[…] The fact that a rectangle with a length of l and a width w has an area of lw is simple, and you almost certainly know it. Try to forget it. Let's imagine that we have no idea that the area of a rectangle is the product of its length and width.
Suppose we know roughly what we mean by "area" in the non-mathematical sense. In other words, we know it's a word that describes how big a two-dimensional thing is, but we don't know how to relate this concept to something mathematical. At this stage, we can use the abbreviation A (area) for area and write a useless phrase like A = ? , but no more. However, based on our everyday non-mathematical representation, we know the following for certain.
The first consideration of our everyday representation. Whatever we mean by the area of a rectangle, it somehow depends on its length and width. If someone has a definition of area that doesn't include length and width, that's nice, but that's not what we mean by area. nine0005
If someone has a definition of area that doesn't include length and width, that's nice, but that's not what we mean by area. nine0005
Think of an abbreviation for these words. We can express the above in an extremely condensed form by writing:
A (l, w) = ?
instead of A = ? as above. The new something inside the brackets says: “It depends somehow on the length and width, and we will reduce them to l and w . I don't know anything else."
[…]
Since we are building the exact mathematical concept of area, starting with an intuitive everyday representation, we have no numbers to start from. If we don't have anything quantitative to start with, we have to start with a qualitative one. Since there are no laws to tell us what to do, we want to ensure that our precise concept matches our everyday one. Let's see what else our everyday mathematical representation says. nine0005
The second consideration of our everyday representation. Whatever we mean by the area of a rectangle, if we double the width without changing the length, we will have two copies of the original rectangle and the area will double. If someone has a definition of area that doesn't behave like this, that's nice, of course, but that's not what we mean by area.
Whatever we mean by the area of a rectangle, if we double the width without changing the length, we will have two copies of the original rectangle and the area will double. If someone has a definition of area that doesn't behave like this, that's nice, of course, but that's not what we mean by area.
Whatever we mean by area, if we double the width of a rectangle without changing the length, the area must double. show: if we double the width, the area will double (leave the length unchanged for now). We can write this idea like this:
A (l, 2w) = 2A (l, w).
For the same reasons, if we double the length without changing the width, the area will also double. We can shorten it like this:
A (2l, w) = 2A (l, w).
Doubling is not required in this sentence. If we triple the width, then we get three copies of the original piece and the area triples. The same can be said about length, quadrupling, or multiplying by any other whole number. What about non-integer numbers? Let's say if we change the length from l to "one and a half l " (without changing the width), then we get one and a half copies of the original figure; accordingly, the area should be one and a half times larger than the original. It turns out that whatever we mean by area, sentences of this kind reflect our intuition that the amount of increase is not important. We can write this whole infinite set of sentences at once like this:
What about non-integer numbers? Let's say if we change the length from l to "one and a half l " (without changing the width), then we get one and a half copies of the original figure; accordingly, the area should be one and a half times larger than the original. It turns out that whatever we mean by area, sentences of this kind reflect our intuition that the amount of increase is not important. We can write this whole infinite set of sentences at once like this:
A (#l, w) = #A (l, w) (1.1)
and
A (l, #w) = #A ( l, w) (1.2)
[…]
Equations 1.1 and 1.2 tell us that we can pull numbers from the Area Calculation Machine regardless of their value. But if this is true, nothing prevents us from being dexterous and pulling out the length and width ourselves! After all, they are just numbers. Since l is the same as l ⋅ 1, and w is the same as w ⋅ 1, we can quietly use both facts from equations 1. 1 and 1.2 for the numbers l themselves nine0024 It turns out like this:
1 and 1.2 for the numbers l themselves nine0024 It turns out like this:
A (l,w)= lA (1,w)= lwA (1,1). (1.3)
And this shows that the area of the rectangle is the length times the width... and something else. What is A (1, 1) doing here?!
It turns out that equation 1.3 shows us the concept of units of measurement. It says that we can find out the area of any rectangle, but only after we set the area of a single rectangle - with length 1 and width 1 (or whatever). If we measured lengths in light years, we would like A (1, 1) would be the area of one square light year. If we measured lengths in nanometers, we would like A (1, 1) to be the area of one square nanometer.
We usually get out of this situation by assuming that A (1, 1) should be 1. But this is just for convenience. We could choose to have A (1, 1) represent the number 27 if we wanted, and then we would have the formula A (l, w) = 27lw .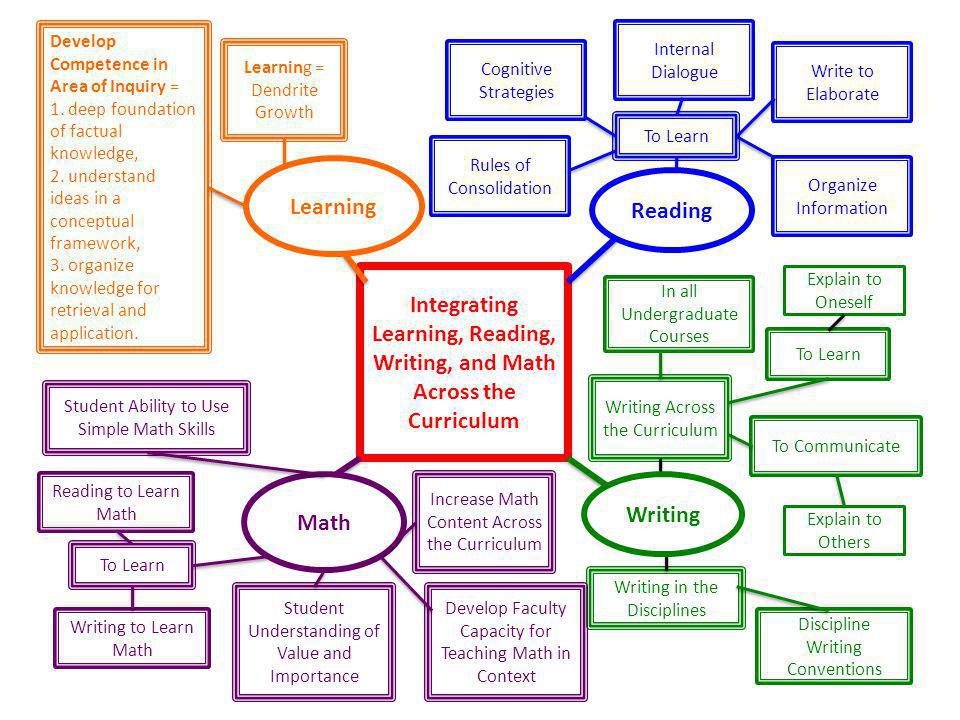 It looks strange, but there is no error here. Instead of being forced to count A (1, 1) as a unit or some other number, we can interpret equation 1.3 differently:
It looks strange, but there is no error here. Instead of being forced to count A (1, 1) as a unit or some other number, we can interpret equation 1.3 differently:
This shows that we do not need to talk about units (in other words, decide what A (1, 1) should be at our request), but we can no longer talk about the squares themselves. This interpretation says that something equals the length times the width, but it is not the area. This is the "ratio" of areas, or how many times can you fit A (1, 1) into A (l, w) .
[…]
It is easy to see that the same argument will work in any number of dimensions. Let's imagine that we have a three-dimensional thing like a box, and denote its length, width and height as l, w and h . For the same reasons as for a rectangle, if we double, for example, the height without changing the length and width, we get two original boxes, and the volume should double. As before, it is not necessary to double exactly, you can increase it any number of times. The same for length and width. Accordingly, in three dimensions, such statements are true for any number #, which is not necessarily the same in the following three sentences:
The same for length and width. Accordingly, in three dimensions, such statements are true for any number #, which is not necessarily the same in the following three sentences:
V (#l, w, h) = #V (l, w, h),
V (l, #w, h) = #V (l, w, h),
V(l, w, #h) = #V(l, w, h).
As before, we can use these ideas for the numbers l, w and h themselves and write:
V (l, w, h) = lwh⋅V (1, 1, 1).
Now we can do something weirder and more interesting: start talking about higher-dimensional spaces. If n is some big number, we can't draw anything in n-dimensional space. Nobody is actually can't. At this stage, we are not even quite sure that we mean by the expression " n -dimensional space". Fine! Nobody bothers to say: “Whatever I mean by n -dimensional space and n -dimensional version of a rectangular thing like a box, they should behave similarly enough to their “relatives” in two and three dimensions, and we can apply the same arguments as just used. And if they don't behave like that, that's just not what I mean by now n -dimensional space". Then we can emphatically write:
And if they don't behave like that, that's just not what I mean by now n -dimensional space". Then we can emphatically write:
V (l1, l2,… , ln) = l1l2⋅⋅⋅ln⋅V (1, 1,… , 1),
where V stands for "what we wish to call volume in n -dimensional space". Moreover, we decided not to give all directions their own strange names, as for two and three dimensions. It's easier to shorten them to the letter l , and then attach different numbers to each to call them separately (l1, l2, ..., ln).
[…]
So we see that in the process of thinking about our everyday concept of area while reducing our thoughts in a way that reduces infinitely many sentences into one, our vague ideas led to the fact that the area of rectangle should be lw A ( eleven). So we discovered not only the familiar formula "length times width", but also one more thing that we forgot to consider: the concept of units of measurement. However, mathematics kindly reminded us of this. nine0005
nine0005
[…]
1.2.2. How to Do It Wrong: An Instruction on the Foolishness of Memory
But it took several years before I realized that teaching science is really hard work. The goal should not be to implant in the student's head the facts that the teacher knows; it is necessary to introduce a way of thinking that will allow in the future to master in one year what the teacher studied for two years. Only in this way can we move from one generation to the next. And when I realized this, my teaching style changed: not to give a bunch of fragments, but to analyze only a few problems, but with real depth. nine0024
Edwin Jaynes, Jaynes E. T. A Backward Look to the Future. http://bayes.wustl.edu/etj/articles/ backward.look.pdf.
One of the worst things about many elementary math courses (at least the ones I've taken) is that the instructors somehow become staunch believers that the purpose of the course is to tell you facts. I can no longer agree with this. You will be surprised: what can the course be about, in my opinion, if not about mathematics? This is important, let's say it once and for all and put it in a frame. ❓Why write it in a frame with such a pretentious name? Good question! Full disclosure: when you're writing a book (as I've learned since I started writing), it's fun to show respect for something you love sometimes. This box is a tribute to my favorite textbook, published after the death of the author, the main work of Edwin Jaynes, The Theory of Probability. The logic of science. Perhaps because he died before completing the book, but also because Jaynes was a fiery man and this work is full of his wonderfully soulful personal witticisms and much more that is rarely found in textbooks. For example, "Declaration of Emancipation" in Appendix B. I've always liked this section. Now I am writing my book in tribute to Jaynes. He deserved it. nine0123
I can no longer agree with this. You will be surprised: what can the course be about, in my opinion, if not about mathematics? This is important, let's say it once and for all and put it in a frame. ❓Why write it in a frame with such a pretentious name? Good question! Full disclosure: when you're writing a book (as I've learned since I started writing), it's fun to show respect for something you love sometimes. This box is a tribute to my favorite textbook, published after the death of the author, the main work of Edwin Jaynes, The Theory of Probability. The logic of science. Perhaps because he died before completing the book, but also because Jaynes was a fiery man and this work is full of his wonderfully soulful personal witticisms and much more that is rarely found in textbooks. For example, "Declaration of Emancipation" in Appendix B. I've always liked this section. Now I am writing my book in tribute to Jaynes. He deserved it. nine0123
[…]
Mathematics is a whole world in which there is nothing accidental and where the mind can educate itself in such an intense and clear way that it cannot come out with another discipline. What's more, as you train your mind, you'll learn along the way a subject that happens to describe everything in the world. This is incredibly useful, but such practicality is a side effect of mind training. If we talk about what is useful and worth putting in a frame, here's something else that you will never be told.
What's more, as you train your mind, you'll learn along the way a subject that happens to describe everything in the world. This is incredibly useful, but such practicality is a side effect of mind training. If we talk about what is useful and worth putting in a frame, here's something else that you will never be told.
Once we understand this, we immediately notice two things. First, it's obvious why training the mind in this way is beneficial, no matter what you do. Secondly, it is obvious that mathematics courses focus on exactly the wrong things. nine0005
Let's study a specific example. In algebra classes, class-filled sleepy students are taught about something called the FOIL method. This stands for First, Outer, Inner, Last - "first, outer, inner, last." transl.
This is a rule for remembering sentences like:
(a + b)2 = a2 + 2ab + b2
or, more generally,
(a + b) (c + d) = ac + ad + bc + bd.
We already see that FOIL is a way to help you remember a fact about math, rather than rediscovering it every time you need it. What is the point here? Most students can see her better than teachers: she's not here. Let's invent both facts so that we never have to remember them again.
What is the point here? Most students can see her better than teachers: she's not here. Let's invent both facts so that we never have to remember them again.
Fig. 1.4. Here, in fact, everything that the FOIL 9 rule says0005
If we take a sheet of paper and draw a picture on it, it will not change the area of the sheet. It doesn't matter what we depict: a house, a dragon or something else. Let's say we're experimenting with the ideas we've found and stumble upon what looks like (a + b)2. We can think of this as the area of a square.
If a square has side length tili-tili , its area is ( tili-tili ) · ( tili-tili ), or ( tili-tili )2. So we can think about ( a + b )2 as for the area of a square with a side ( a + b ). Let's draw this square, and then add a picture to it, as in Fig. 1.4. It looks like something lopsided with signatures, but these are just two straight lines that divide the sides into parts with lengths a and b .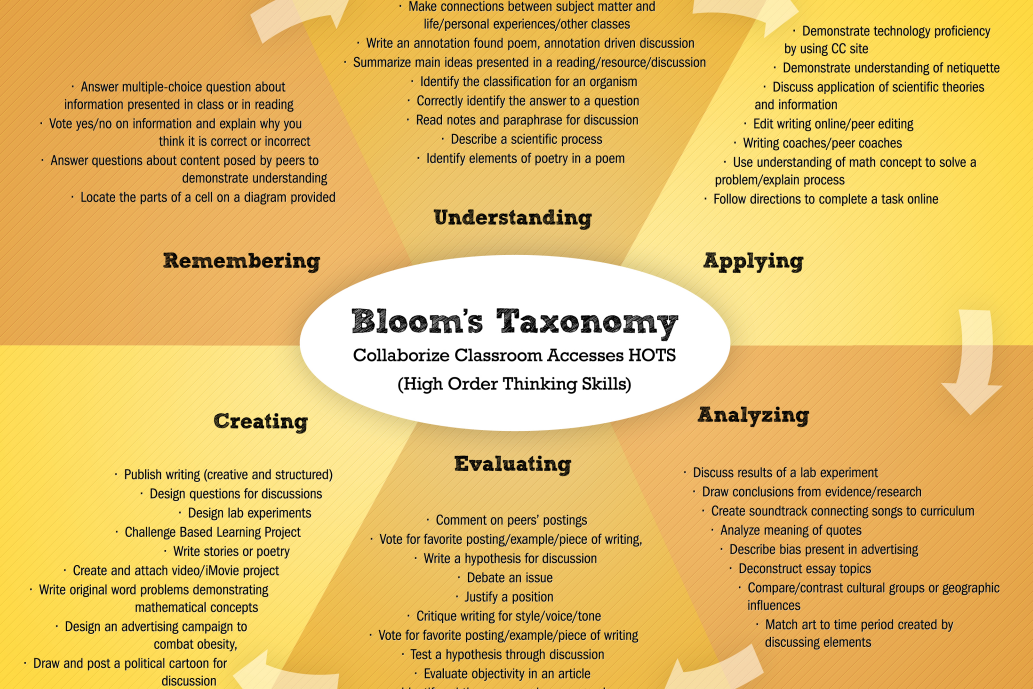 This makes it possible to talk about the same thing in two ways. Since drawing lines on a square does not change its area, we see that:
This makes it possible to talk about the same thing in two ways. Since drawing lines on a square does not change its area, we see that:
(a + b)2 = a2 + 2ab + b2.
Now you don't need to remember this formula. Let's see if we can invent a more complex one in the same way:
(a + b) (c + d) = ac + ad + bc + bd.
Fig. 1.5. Here, really, everything that the FOIL rule says
Any two multiplied numbers, that is, in general form ( tili-tili ) ⋅ ( trali-vali ), can be represented as the area of a rectangle with sides of length tili-tili and trali - Vali. Draw a picture where ( tili-tili ) is ( a + b ) and ( trali-wali ) is ( c + d ). Look at fig. 1.5. It shows that the area of the large rectangle is the sum of the areas of all the small ones. The essence of the picture can be expressed in a compressed form:
(a + b) (c + d) = ac + ad + bc + bd.
Now you don't need to remember this formula. If you forget it, you can reinvent it. You don't even have to try to memorize these formulas. Better even try to forget them immediately! In each math classroom, an inscription should be posted above the board:
If you forget it, you can reinvent it. You don't even have to try to memorize these formulas. Better even try to forget them immediately! In each math classroom, an inscription should be posted above the board:
Since your goal is to follow the path of reasoning on your own, you should not memorize the steps in this derivation, it is better to understand its essence well, so that if you forget any formula (which should do ) you can immediately reinvent it in a few seconds . When you do this, you find yourself "remembering" things inadvertently, simply because you understand them well. To test if this Zen process of "learning without memorization" has been successful for you, you can test whether you can apply this line of reasoning to something new ?
The logic is this: if you can apply the same reasoning to new areas you've never seen, you won't just memorize facts
The new context acts like a sieve that weeds out that possibility. Unfortunately, in an environment that punishes experimentation and failure (such as in school), testing things in new contexts becomes more of a source of anxiety rather than the intellectually satisfying game it should be. Let's forget all this and just play. nine0005
Unfortunately, in an environment that punishes experimentation and failure (such as in school), testing things in new contexts becomes more of a source of anxiety rather than the intellectually satisfying game it should be. Let's forget all this and just play. nine0005
Inventing something
Above, we discussed the silly acronym FOIL for the First, Outer, Inner, Last construct. This method of remembering the fact rather than understanding the process leads us to create numerous "methods" and we will have to remember them. For example, it is true:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac.
This is an ugly sentence and no one in their right mind would want to memorize it. If our goal was just to capture this, rather than understand general reasoning strategies, we could take the same approach as the guy who invented the FOIL acronym and call it the LT.MT.RT.15.16.24.26.34.355 method. Let's not do that. Instead, use the same strategy as above (drawing a picture and looking at it carefully) to invent this ugly expression for yourself. Hint: draw a square and divide each side into three parts instead of two as before. nine0005
Hint: draw a square and divide each side into three parts instead of two as before. nine0005
Now it's time to play around in three dimensions and see if the same reasoning doesn't work here. We really don't want to remember an ugly sentence like this:
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Instead of memorizing this, let's invent it in the same way as before: draw a picture and look at it carefully. Hint: draw a cube and divide each side into two parts. Study fig. 1.6. Try the first example first: it's harder to visualize in this case, and if you get stuck, it's easy to get discouraged and think you don't get the idea when you really do. nine0005
Fig. 1.6. This picture may help in inventing the formula in 2
Although this method of reasoning allows us to invent things that others have asked us to remember, there are two unfortunate circumstances. First, it's not that easy (I'll explain why shortly). Secondly, it's basically useless for things like (a + b)4 or (a + b)100 , since it's hard for the human mind to visually represent objects if there are more than three dimensions.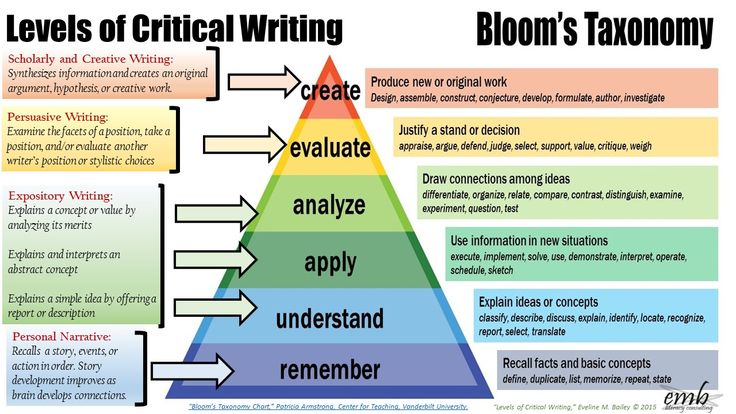 It turns out that there is a remedy for both problems. nine0005
It turns out that there is a remedy for both problems. nine0005
[…]
Suppose we have a sheet of paper. Imagine that it is torn into two arbitrary parts. Even if we do not know anything about areas numerically, it is clear that the area of the original sheet is equal to the sum of the areas of the two scraps. We can rediscover the FOIL method and all its more complex variants in any number of dimensions (regardless of whether we are able to draw a suitable picture or not) simply by applying the idea of tearing over and over again. Let's write it in an abbreviated form.
Fig. 1.7. The obvious law of tearing: if you tear something into two parts, the area of the original object will be equal to the sum of the areas of these two fragments. We can say it in short: (a + b) ⋅ (something) = a ⋅ (something) + b ⋅ (something). Textbooks usually call this "distributive law"
Let's say we're inventing something and we get to the point where we write something like (something) ⋅ (a + b) or perhaps (a + b) ⋅ (something) . It's the same thing, the reasoning works for both cases. Suppose, as before, we can represent this as the area of a rectangle whose two sides are (something) and the other two are (a + b) . If we tear it exactly along the line, as shown in fig. 1.7, we get one piece with an area of a ⋅ (something) and the second square b ⋅ (something) . This doesn't change the total area (we're not throwing away any parts), so the following must be true:
It's the same thing, the reasoning works for both cases. Suppose, as before, we can represent this as the area of a rectangle whose two sides are (something) and the other two are (a + b) . If we tear it exactly along the line, as shown in fig. 1.7, we get one piece with an area of a ⋅ (something) and the second square b ⋅ (something) . This doesn't change the total area (we're not throwing away any parts), so the following must be true:
(a + b) ⋅ (something) = a ⋅ (something) + b ⋅ (something).
I will call this the obvious law of tearing things apart, but the name is not important here. Call it whatever you want. Textbooks use the term "distributive law". It sounds pretentious, but such a name also makes sense. […]
Now, if we want everything to look like in a textbook, we can write the letter c instead of 9 in the obvious law0023 (something) . This is fine too, I wrote (something) to remind you that the law is true no matter what (something) looks like. If it turned out to be the sum of two things (or if we wanted to put it that way), we could replace (something) with something like (c + d) and rewrite the obvious law:
If it turned out to be the sum of two things (or if we wanted to put it that way), we could replace (something) with something like (c + d) and rewrite the obvious law:
(a + b) ⋅ (c + d) = a ⋅ (c + d) + b ⋅ (c + d).
However, using the obvious law again (for each of the parts on the right), we get:
(a + b) ⋅ (c + d) = ac + ad + bc + bd,
that is exactly the expression that we invented earlier when drawing pictures. The above sentence is also a FOIL method. But since we invented it by means of an obvious law, we don't need to memorize it. Ready, attention, forget it forever!
An obvious law looks ordinary. In addition, it turns out that he offers us a window into higher dimensions. The visual way of thinking about (a + b)3 requires drawing a 3D object (a cube), and we quickly notice that the method doesn't help us much for (a + b)4 or any higher powers, because we cannot imagine four-dimensional objects. But even if we're not interested in algebraic tedium like decomposing (a + b)4 for our own benefit, we might be interested in deeper questions, such as how to cut a four-dimensional cube along each of the three-dimensional "surfaces" none of which we can represent due to the limitations of the human brain. But it is we primates who are faced with the problems of the visual method, and the obvious law has no such limitation. Therefore, if desired, we could apply the obvious law to something like a decomposition (a + b)4 several times, and once we have completely unraveled it, the resulting (very long) expression would provide us with a little insight into four-dimensional geometry. For example, the number of terms in the final expression would be the number of pieces into which a four-dimensional cube can be cut along three-dimensional planes. I have no idea how to portray what I just said, but it's true! So should be . Just by using the everyday fact of tearing a rectangle in two, we can coax a mathematician into telling us something that is far beyond the imaging capabilities of the human brain.
But even if we're not interested in algebraic tedium like decomposing (a + b)4 for our own benefit, we might be interested in deeper questions, such as how to cut a four-dimensional cube along each of the three-dimensional "surfaces" none of which we can represent due to the limitations of the human brain. But it is we primates who are faced with the problems of the visual method, and the obvious law has no such limitation. Therefore, if desired, we could apply the obvious law to something like a decomposition (a + b)4 several times, and once we have completely unraveled it, the resulting (very long) expression would provide us with a little insight into four-dimensional geometry. For example, the number of terms in the final expression would be the number of pieces into which a four-dimensional cube can be cut along three-dimensional planes. I have no idea how to portray what I just said, but it's true! So should be . Just by using the everyday fact of tearing a rectangle in two, we can coax a mathematician into telling us something that is far beyond the imaging capabilities of the human brain.