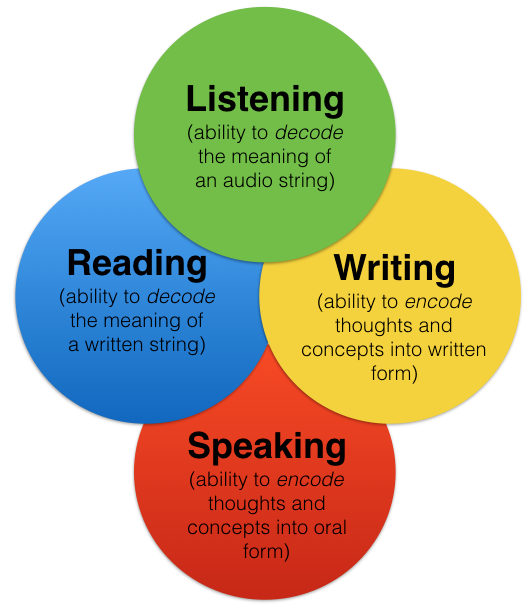
What are concepts in mathematics

How Math Concepts and Math Skills Work Together and Why You Should Care

Sometimes people use the words “math skills” and “math concepts” interchangeably. They are not the same, but they do go hand and hand. Understanding how new math skills and concepts work together will give you a new perspective on math education and math challenges.

Definition of Skills
Skills are actions. People do them. People master math skills the same way they master musical skills or sports skills. They practice the actions and steps intentionally, correctly and frequently. They may even go to a special place to practice the skill.

Definition of Concepts
Concepts are ideas. People understand them. People learn concepts by thinking, discussing, reading, listening and/or writing about them.

Similarities Between Skills and Concepts
Both can be learned and they are each the point of education.
Both have a natural progression, or order, in which they should be taught.
Both are a huge component of math success.

1. Education
Most of education focuses on skills. Skills are easier to observe and grade because a person can demonstrate skills. Proving that you understand a concept is difficult. Teachers try to measure a student’s understanding by asking them to write about, discuss or draw concepts. Even then, students are still limited in showing their understanding by their language, writing or artistic skills. For example, most adults in the U.S. understand the concept of basic nutrition. How many adults in the U.S. could explain basic nutrition in a foreign language? Our limited skill set in the foreign language would limit how well we could prove our understanding.

Retaining concepts is easier than retaining skills. What happens when we don’t practice a skill? We lose the skill. Most adults can think of a skill that they frequently practiced as child, but don’t practice now (piano for example). Chances are that their younger selves were much better at that skill than their current self.

If you understand a concept, you have that understanding forever. You may need to think about it before you remember all the details, but the underlying concept will always be there. You will always be able to build upon the concepts you understand and your previous understanding makes learning easier and faster.

2. Progression
Skills build on top of each other. When learning to swim, most children learn to float around the same time as learning to flutter kick. They are both beginning level skills. They must master all the beginning level skills before attempting an advanced skill, like swimming in open water or attempting the butterfly stroke.

Concepts are also best taught progressively. Our brains use neural pathways to make connections. Our understanding of underlying concepts pave the way for understanding new concepts. The deeper and broader our knowledge base is, the easier it is for us to connect it to new concepts.

3. Math Success
Skills are the “how-to” parts of math. Children should master adding and subtracting before starting multiplication. They must know how to multiply and divide before attempting percentages.

Concepts are the underlying ideas of math. Concepts are ideas like equality and symbolic representation. Many math concepts build upon each other. A child who has a solid understanding of the relationship of quantity and numbers, or “number sense”, will find the concept of “wholes and parts”, naturally makes sense.

How Skills and Concepts Work Together
Understanding concepts makes learning skills easier. Mastering skills, especially thinking skills, makes learning concepts easier. Each prepares the brain differently.

People might be able to do a skill without understanding “why” it works. Understanding why a skill works in sports is helpful, but not critical. Can you imagine swim lessons at the neighborhood pool to 5 year-olds including a study of fluid dynamics and propulsion?

People might also have a concept about something, without the skill to execute it. Many adults understand the concept of bacteria and wound maintenance, but they still go to a skilled professional to get stitches. Some people call this “book smarts” versus “street smarts.” Understanding the why helps you build your knowledge base and your retention of skills.

Most people in life don’t care about what others understand. They care about what others do. A conceptual understanding helps build skill sets faster.

How Skills and Concepts Work Together in Math
Math skills and concepts should be taught simultaneously. Children who learn math skills without learning the underlying concepts, will find math can get very confusing. Their lack of understanding will limit their ability to apply math in a variety of problem solving situations. Without understanding a concept, we are forced to rely on remembering and practicing a skill. For example, let’s say a 5th grader learned how to divide fractions using the "copy, dot, flip" method but never understood the concept behind why that process worked. Then the 5th grader progresses to 6th grade and stops practicing dividing fractions because they are learning new skills. When that child stops practicing, he will then likely forget how to divide fractions. This will be a problem when dividing fractions comes up again in algebra and advanced math. The child who has both the skills and the concepts will be much better prepared.

Children who learn math concepts without learning the skills, will struggle to apply what they know. Knowing the difference between concepts and skills helps to identify the problems that arise in math.

How we Approach Skills and Concepts at Mathnasium
At Mathnasium of Littleton we focus on teaching foundational math skills like Counting, Numerical Fluency (adding and subtracting and multiplication facts), time and money and the order of operations while also teaching concepts such as Number Sense, Wholes and Parts, and Proportional Thinking. These latter are concepts that also involve skills. Additionally, thinking is a skill that must be practiced. Thinking skills enable a child to learn the concepts and we never neglect to teach concepts. We encourage our students to ask us questions and we ask them questions to promote deep thinking and conceptual understanding.

The progression of skills and concepts and how they work together is exactly why at Mathnasium of Littleton, we work hard to close math gaps.

For more information about our methods, click here. The result is stronger math skills with a deeper understanding of mathematical concepts. Our motto is: “We Make Math Make Sense!”

Give us a call today! 303-979-9077

Articles referenced in this post:

Practice Makes Perfect so Perfect Practice is Essential

Multiple Practice Sessions Provide Better Learning than Cramming

Where Does your Child Go To Practice Math?

Is Mathematical Understanding Really Necessary?

Worried Your Child has Not Memorized the Multiplication Tables?

4 Tips for Figuring Out Percentages the Easy Way

Learning Math Symbols in Elementary School Takes Time

Prepare Your Child for Calculus Starting in Second Grade

Is Your Child Dependent on Algorithms and is that a Bad Thing?

Why Does Mathnasium of Littleton Focus on Foundational Math Skills?

Counting … Its More Complex Than You Imagine

Teaching Number Sense

Focus on Math: Wholes and Parts

Focus on Math: Proportional Thinking

What is Numerical Fluency?

Multiplication Fluency is Coming to Mathnasium of Littleton

Focus on Math: Learning About Money

Does Your Child Ask Questions in Math Class?

Focus on Math: Order of Operations

Understanding Mathematical Reasoning

Understanding Math Learning Gaps

Basic Concepts in Mathematics | Sciencing

••• Rechenrahmen image by Yvonne Bogdanski from Fotolia. com

Updated April 24, 2017

By Erin Schreiner

Upon entering school, students begin to develop their basic math skills. Mathematics makes it possible for students to solve simple number based problems. Through the use of math, students can add up store purchases, determine necessary quantities of objects and calculate distances. While the discipline of math does become quite complex, there are some basic math skills that every student can and should learn during their math education program.

Number Sense

The first mathematics skill that students learn is basic number sense. Number sense is the order and value of numbers. Through the use of their number sense, students can recall that ten is more than five and that positive numbers indicate a greater value than their negative counterparts. Students commonly begin learning number sense skills in pre-school, and continue developing a more complex understanding of the concept throughout elementary school. Teachers introduce this skill to students by having them order digits and complete basic counting activities. They extend their knowledge by introducing the concept of the greater than and less than symbols and explaining what the use of each indicates.

Addition and Subtraction

The first mathematical operation that students learn is addition, followed closely by subtraction. Students begin studying these skills through the use of manipulatives, or physical tools that represent objects, as early as pre-school, and continue building their skills, adding and subtracting ever larger numbers through elementary school. When the skills are initially introduced, students perform rudimentary calculations using single digits. Later in their study, they practice applying these skills through the completion of story problems.

Multiplication and Division

After developing a complex understanding of addition and subtraction, students move on to studying multiplication and division. Depending on the student’s math achievement level, he may begin studying these operations as early as first grade. As with addition, students' study of these operations begins with single digit calculations. As they develop their multiplication and division skills, the problems become increasingly complex, involving larger numbers.

Decimals and Fractions

After students develop a strong understanding of number sense, they explore fractional numbers or numbers that lay between whole digits. Commonly this study begins in first grade with the exploration of basic fractions including ½ and ¼. After learning fractions, including how to add, subtract, divide and multiply non-whole numbers in fraction form, students study decimals. A strong understanding of fractions and decimals is vital, as students will use these non-whole numbers extensively as they continue their math study.

References

NCTM: National Standards by Grade
National Council for the Teachers of Mathematics: Math Skills

About the Author

Erin Schreiner is a freelance writer and teacher who holds a bachelor's degree from Bowling Green State University. She has been actively freelancing since 2008. Schreiner previously worked for a London-based freelance firm. Her work appears on eHow, Trails.com and RedEnvelope. She currently teaches writing to middle school students in Ohio and works on her writing craft regularly.

Photo Credits

Rechenrahmen image by Yvonne Bogdanski from Fotolia.com

1. Mathematical concepts

Lecture #2

in mathematics

Topic: "Mathematical concepts”

Plan:

Mathematical concepts
Scope and content concepts. Relations between concepts
Definition concepts
Requirements to definition of concepts
Some species definitions

concepts, which are studied in the initial course mathematics is usually represented in the form four groups. The first one includes concepts related to numbers and operations above them: number, addition, term, more, etc. The second includes algebraic concepts: expression, equality, equation and others. The third is geometric concepts: line, segment, triangle etc. The fourth group is formed by the concepts associated with quantities and their measurement.

How to study such an abundance of different concepts?

Before All you need to do is to understand the concept as a logical category and features mathematical concepts.

AT logic concepts are considered as a form thoughts reflecting objects (objects or phenomena) in their essential and general properties. The language form of the concept is a word or group of words.

Compose the concept of an object means to be able to to distinguish it from others similar to it objects. Mathematical concepts have a number of features. home is that the mathematical objects to be compiled concept does not exist in reality. Mathematical objects are created by the mind person. These are ideal objects reflecting real objects or phenomena. For example, in geometry one studies the shape and size of objects, without taking into account their other properties: color, mass, hardness, etc. From all this distracted, abstracted. That's why in geometry instead of the word "object" say "geometric figure".

result abstractions are and such mathematical concepts like "number" and "value".

Generally mathematical objects exist only in the thinking of man and in those signs and symbols that form a mathematical language.

To It can be added to what has been said that, by studying spatial forms and quantitative relations of the material world, mathematics not only uses different methods abstraction, but abstraction itself acts as a multi-step process. Mathematics considers not only concepts that emerged in the study real objects, but also concepts arising from the first. For example, the general concept of a function as a correspondence is a generalization of the concepts of specific functions, i.e. abstraction from abstractions.

To master general approaches to learning concepts in the elementary course of mathematics, The teacher needs knowledge about the volume and the content of the concept, about the relationship between concepts and about the types of definitions of concepts.

Any mathematical object has certain properties. For example, a square has four sides right angles equal to diagonals. Can specify other properties.

Among the properties object distinguish between essential and insignificant. Property feel essential to an object if it inherent in this object and without it, it is not may exist. For example, for square essential are all the properties mentioned above. Not essential for square ABCD property "side AD horizontal." If the square is turned then side AD will be located differently (Fig. 26).

That's why, to understand what is given mathematical object know its essential properties.

When talking about a mathematical concept, then usually means a set of objects, denoted by one term (word or group of words). So, speaking of a square, refers to all geometric shapes, which are squares. Think that the set of all squares is the scope of the concept of "square".

Generally volume concepts are the set of all objects, denoted by one term.

Any concept has not only volume, but also content.

Contents concepts are the set of all essential object properties reflected in this concept .

Consider, For example, the concept of "rectangle".

Volume concepts are many different rectangles, and in its content includes such properties of rectangles, how "to have four right angles", "to have equal opposite sides", "to have equal diagonals”, etc.

Between scope of the concept and its content there is a relationship: if increases the scope of the concept, then it decreases content and vice versa. For example, the scope of the concept of "square" is part of volume of the concept of "rectangle", and in the content of the concept of "square" contains more properties than in the content of the concept "rectangle" ("all sides are equal", diagonals are mutually perpendicular and etc.).

Any the concept cannot be grasped without realizing it relationships with other concepts. That's why it is important to know in what respects to be concepts, and to be able to establish these connections.

Relations between concepts are closely related to relationships between their volumes, i.e. sets.

Let's agree concepts are capitalized Latin alphabet: a, b, c,...,z.

Let two concepts a and b are given. Their volumes will be denoted respectively by A and V.

If a BUT B (A ≠ B), then they say that the concept of a - specific in relation to the concept b , a concept b - generic in relation to the concept a .

For example, if a is a "rectangle", b - "quadrilateral", then their volumes A and B are in relation to inclusion (A B and A ≠ B), since every rectangle is a quadrilateral. That's why it can be argued that the concept "rectangle" - specific in relation to to the concept of "quadrilateral", and the concept "quadrangle" - generic in relation to the concept of a rectangle.

If a A = B, then they say that concepts a and b are identical.

For example, identical concept of "equilateral triangle" and "equiangular triangle" because their volumes match.

If a sets A and B are not related inclusions, then we say that the concepts a and b are not related to genus and species and are not identical. For example, not related such relations of the concept of "triangle" and "rectangle".

Consider in more detail the relation of genus and species between concepts. First, the concepts of gender and species are relative: the same concept may be generic to one concept and species in relation to another. For example, the concept of "rectangle" - generic in relation to the concept of "square" and specific in relation to the concept "quadrilateral".

Secondly, for a given concept, one can often specify several generic terms. Yes, for the concepts of "rectangle" are generic are the concepts of "quadrilateral", parallelogram, polygon. Among them, you can specify the nearest. For the concept of "rectangle" to the nearest is the concept of "parallelogram".

Thirdly, the species concept has all the properties generic concept. For example, a square being a species concept in relation to to the concept of "rectangle", has all the properties of a rectangle.

Since the volume concepts - set, convenient, setting relations between the volumes of concepts, depict them using Euler circles.

Set, for example, relationship between the following couples concepts a and b, if:

1) a - "rectangle", b - "rhombus";

2) a - "polygon", b - "parallelogram";

3) a - "straight", b - "line segment".

AT case 1) the volumes of concepts intersect, but not one set is a subset of another (Fig. 27).

Consequently, It can be argued that these concepts and b are not related to genus and species.

AT case 2) the data volumes of the concept are regarding inclusion, but do not match - every parallelogram is polygon, but not vice versa (Fig. 28). Therefore, it can be argued that the concept of "parallelogram" - specific in relation to the concept of "polygon", and the concept of "polygon" is generic in relation to the concept of "parallelogram".

AT case 3) the volumes of concepts do not intersect, since not a single segment is possible say he is direct, and neither one line cannot be named segment (Fig. 29).

Consequently, these terms are not related genus and species.

O concepts of "line" and "segment" can be say they are for whole and part: A segment is a part of a line, not a type of it. And if the species concept has all the properties generic concept, then the part is not necessarily has all the properties of the whole. For example, a segment does not have such property of the straight line, as its infinity.

Topic 7. Mathematical concepts Content

Mathematical concepts. The scope and content of the concept.
Relations genus and species between concepts.
Definition concepts.
Requirements to the definition of concepts.

5. Implicit definitions

Main literature 7, 14, 16, 24, 25, 30, 33, 34;

Additional literature 26, 44

studying mathematics at school, college, university, need to learn a certain system concepts, propositions and proofs, but to master this system and then successfully apply acquired knowledge and skills, teaching younger students and solving the problem of their development by means mathematics, one must first understand what features of mathematical concepts, how their definitions, sentences, expressing properties of concepts, and proof of.

Any mathematical object has certain properties. For example, a square has four sides right angles equal to diagonals. Can specify other properties of the square.

Among properties of an object distinguish between properties essential and minor to distinguish it from other objects. The property is considered significant for object, if it is inherent in this object and without it it cannot exist. Insignificant properties are those properties, the absence of which does not affect the existence of the object. So, for example, the named properties of a square are essential, and the property "side AB of the square is vertical" insignificant. If the square is turned then side AB will be located differently (Fig. 1).

AT C

BUT C

BUT D

D Rice. 1

That's why, to understand what is given mathematical object is enough know its essential properties. In that case, it is said that there is a concept of this object.

When talk about a mathematical object, then usually mean the whole objects designated by one term, word, name. So when talking about square, then they mean all geometric shapes that are squares. Aggregate of all squares is the scope of the concept square.

Definition. The scope of a concept is the totality of all objects designated by the same term.

Any concept has not only scope, but also content.

Definition . The content of the concept is a set all essential properties of the object, reflected in this concept.

T. Well, every concept is characterized by term, volume, content.

Note. Between the scope of a concept and its content there is a connection: the "larger" volume concept, the "less" its content, and vice versa.

Example

Volume concept of "right triangle" "less than" the scope of the concept of "triangle", since the scope of the first concept includes not all triangles, but only rectangular ones.