What are number concepts
Number Concepts Grade 5 | Essential Skills Educational Software
Designed for: Grade 5
Understanding place value, rounding, skip counting, recognizing large numbers, working with decimals, fractions and problem solving are among the skills covered in this grade 5 math program. Rules and examples are provided to introduce new concepts.
Previous Next
Targeted Skills
- Understanding Place Value
- Rounding
- Skip Counting
- Recognizing Large Numbers
- Working With Decimals
- Fractions And Problem Solving
Highlighted Features
- Working with numbers to 1,000,000, standard and expanded form, place value, skip counting and rounding are some of the skills covered in this comprehensive program
- Students will compare and reduce unlike denominator fractions
- Provides practice in the addition and subtraction of fractions
- Students will solve interesting real-world problems
- Rules and examples provided for each new concept
- Students learn to convert between decimals and fractions
- Provides instruction and practice in working with decimals to thousandths
Try Number Concepts Grade 5 Risk Free for 45 Days!
We're so confident that you'll love your Essential Skills software, we'll give you 45 days to try it out before you even pay!
Here's how it works:
- Place your order (no purchase order necessary)
- Try the software risk free for 45 days
- Pay the invoice at the end of the 45 days, or cancel and pay nothing
To order online, simply choose one of the license types below.
You will have the option for us to invoice your school, or you can pay using a credit card. To order by phone, call 1-800-753-3727, or fax your order to 1-800-723-7718. We accept purchase orders, but they are not required.
Annual Web-Based Subscriptions
PC and Mac (System Requirements)
This software is available in web-based format. The perpetual licensed version above is a one-time purchase which you can use over and over, with no subscription charges or renewal fees. The web-based version is a low-cost yearly subscription, which requires no installation or configuration on your network.
Have less than 25 students? Get the entire catalog of Essential Skills web-based programs for $55 per student (5 student minimum)
Request a Quote
25 Students or Less
Web-Based Subscription
$89.
00 Per Year- No installation or configuration required
- Up to 25 unique users at an individual school
Add to Cart
26 - 50 Students
Web-Based Subscription
$129.00
Per Year- No installation or configuration required
- Up to 50 unique users at an individual school
Add to Cart
51 - 100 Students
Web-Based Subscription
$189.00
Per Year- No installation or configuration required
- Up to 100 unique users at an individual school
Add to Cart
101 - 200 Students
Web-Based Subscription
$239.
00 Per Year
- No installation or configuration required
- Up to 200 unique users at an individual school
Add to Cart
201-300 Students
Web-Based Subscription
$319.00
Per Year- No installation or configuration required
- Up to 300 unique users at an individual school
Add to Cart
301-500 Students
Web-Based Subscription
$489.00
Per Year- No installation or configuration required
- Up to 500 unique users at an individual school
Add to Cart
500+ Students
Web-Based Subscription
$639.
00 Per Year- No installation or configuration required
- 500 or more unique users at an individual school
Add to Cart
Perpetual CD Licenses
PC and Mac (System Requirements)
Single (CD)
For use on a single workstation
$119
Perpetual License- No subscription charges or renewal fees
Add to Cart
Lab Pack (CD)
For use on any five (5) workstations simultaneously
$394
Perpetual License- No subscription charges or renewal fees
Add to Cart
Site License (CD)
For unlimited use on all workstations at an individual school
$826
Perpetual License- No subscription charges or renewal fees
Add to Cart
What are Pre-Number concepts | Vikas sharma education
Pre-Number concepts are those which concepts should be learn before learning Numbers.
We all agree on their importance but do we agree what are the pre number concepts?
If we are so much non aligning on content then it raises the question on alignment with perception and pedagogy.
I often asked teachers two questions-
What are pre number concepts?
Why is it necessary to teach?
I received answers in a wide range and quiet contradictory. They are differing on these, so I tried in this article to bring clarity on this.
One criterion is grade wise classification of mathematical concepts, concepts which are taught in kindergarten, play school can be called pre number concepts. Like – matching, sorting, categorization, grouping, odd one out etc.
Let’s look some examples from Nipun bharat, NCERT, and state documents-
As per Nipun Bharat Numeracy have been put into 7 major themes: i. Pre-Number concepts ii. Numbers and operations on numbers iii. Shapes and Spatial Understanding iv. Measurement v. Patterns vi. Data Handling vii. Mathematical Communication.
Pre-Number concepts- Mathematicians and psychologists have often argued that before children start counting objects or develop an understanding of number, they need to be able to classify, order and set up one-to-one correspondences to some extent. Since these skills are preliminary to the understanding of numbers, they are called as pre-number concept.
In preschool curriculum, NCERT – Sensory Development, Cognitive skills, Concept formations, Number sense, concept related to the environment, use of the technology are under key concepts or skills.
Utter Pradesh Prerna Suchi describe first class learning out come students can classify objects on the basis of big-small, before-after, far-near etc under pre number concepts.
Now, we can classification in two category of Pre number concepts-
First one is Big-small, far-near, right-left, up -down, thin-fat etc.
Second one is One to one corresponding, comparison, classification, sequencing, seriation and grading etc.
First list is more about spatial understanding which should be suited age wise and grade wise, we can say these skills preschool maths, play school maths, kindergarten maths. These are part of overarching aims of preschool education are: z providing strong foundations for all round development and life-long learning. preparing the child for school.
Second list is directly associated to number sense or help achieving number sense skills. These should be called pre number concepts.
Children to engage with before they begin to tackle work involving actual numbers. These activities have come to be known as “pre–number activities“, and are considered to be essential pre-requisites to basic number work.
Here we can try to elaborate pre number concept or pre number skills-
Classification – Classification can be done with any concept such as colour, shapes, size, animals, transport, etc.
Say for example, ask children to keep all yellow blocks on one side, and green blocks on another side. You can begin with simple classification initially with the real objects and gradually with multiple classification. You need to begin with single criteria and gradually moving to two or more criteria for example, asking a child to classify yellow and green fabric pieces, moving to two or more attributes, for example, big yellow fabric pieces and small green fabric pieces. Once a child is able to classify concrete objects, then the skill can be strengthened further, using pictures and other manipulatives.
Compare and Seriation Place 5-6 leaves of different sizes in front of the children. Ask the children (one by one) to sort out and name the biggest and smallest leaf. Then give them 3 more different sized leaves and ask them to seriate in order, biggest to smallest and vice a versa. When the children are able to seriate 3 leaves, increase the number of leaves.
Patterning – Use blocks, beads and other manipulative to build spatial reasoning and pattering skills.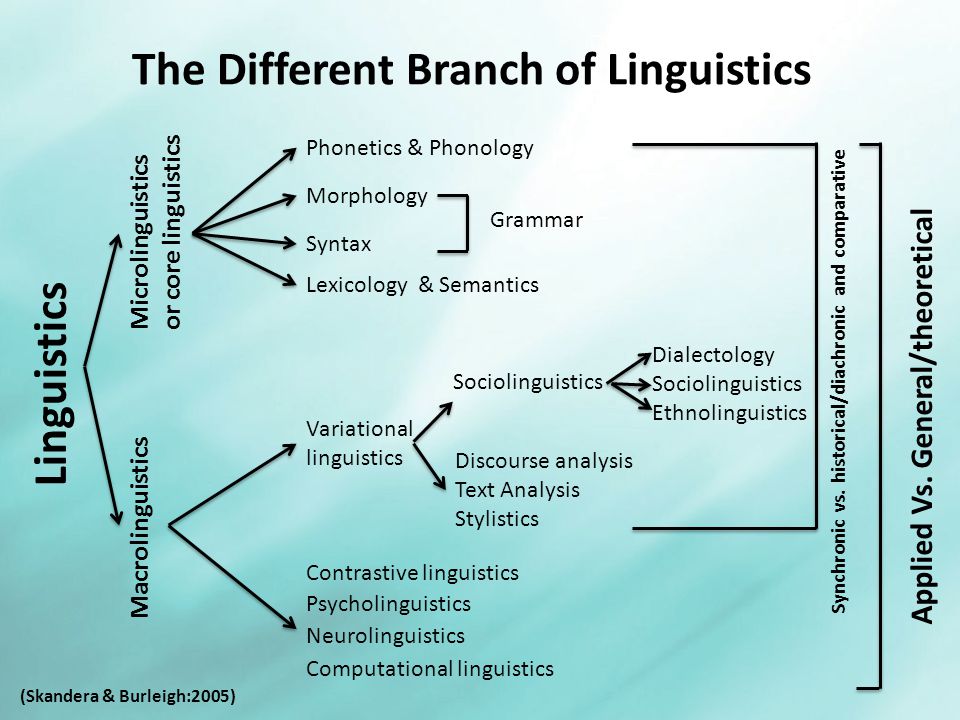
For example, “Threading and patterning activities using colour’. Follow the pattern or copying patterns. Completing the pattern.
Sequential thinking – Sequential thinking cards which the children organise according to the logical sequence of events. Encourage left to right placement of objects or cards. Repeating orally a sequence of three numbers between 1 and 10. What comes next? – “red, red, green, red, red,…” (the child says, “green”).
Seriation: – Putting things in order (biggest to smallest, tallest shortest and on)
One to One Correspondence is referring to the understanding that each object in a group can be counted once and only once, between sets A and B is similarly a pairing of each object in A with one and only one object in B.
Problem solving skill Problem solving activities help pre-schoolers to develop basic problem-solving skills and hand-eye coordination.
Completing simple jigsaw puzzle initially and gradually a difficult one, for example, starting with two-piece puzzle to 5–6-piece puzzle. Puzzle activities can include traditional Inset boards (shapes, animals, transport, birds, fruits ect.)
Pre-Number concepts and Preschool maths are not same, of course pre number concepts would be part of pre school maths along with spatial understanding with their specific meaning and objective.
- More
NUMERIC SEQUENCE | Encyclopedia Around the World
Contents of the article- Properties of numerical sequences.
- Arithmetic progression.
- Geometric progression.
- Sequence limit.
The numerical sequence is the function of the type Y = F ( x ), x about N , where N is many natural numbers (or the function of the natural argument), Y = F ( N ) or Y 1 , Y 2 , ..., Y N , .... The values y 1 , y 2 , y 3 ,… are respectively called the first, second, third, … members of the sequence.
For example, for the function y = n 2 you can write:
y 1 = 1 2 = 1;
y 2 = 2 2 = 4; Sequencing Methods Sequences can be specified in various ways, among which three are especially important: analytical, descriptive and recurrent.
1. A sequence is given analytically if its formula is given n th member:
y n = f ( n ).
Example. y n = 2 n – 1 – sequence of odd numbers: 1, 3, 5, 7, 9, …
what elements the sequence is built.
Example 1. "All members of the sequence are equal to 1." This means that we are talking about a stationary sequence 1, 1, 1, …, 1, ….
Example 2. "The sequence consists of all prime numbers in ascending order." Thus, the sequence 2, 3, 5, 7, 11, … is given. With this way of specifying the sequence in this example, it is difficult to answer what, say, the 1000th element of the sequence is equal to.
3. The recursive way of specifying a sequence is that a rule is specified that allows one to calculate the n th member of the sequence if its previous members are known. The name recurrent method comes from the Latin word recurrere - return.
Most often, in such cases, a formula is indicated that allows expressing the n -th member of the sequence through the previous ones, and 1–2 initial members of the sequence are specified.
Example 1. y 1 = 3; y n = y n –1 + 4 if n = 2, 3, 4,….
Here y 1 = 3; y 2 = 3 + 4 = 7; y 3 = 7 + 4 = 11; ….
It can be seen that the sequence obtained in this example can also be specified analytically: y n = 4 n – 1.
Example 2. y 1 = 1; y 2 = 1; y n = y n –2 + y n
Here: y 1 = 1; y 2 = 1; y 3 = 1 + 1 = 2; y 4 = 1 + 2 = 3; y 5 = 2 + 3 = 5; y 6 = 3 + 5 = 8;
The sequence composed in this example is specially studied in mathematics, since it has a number of interesting properties and applications.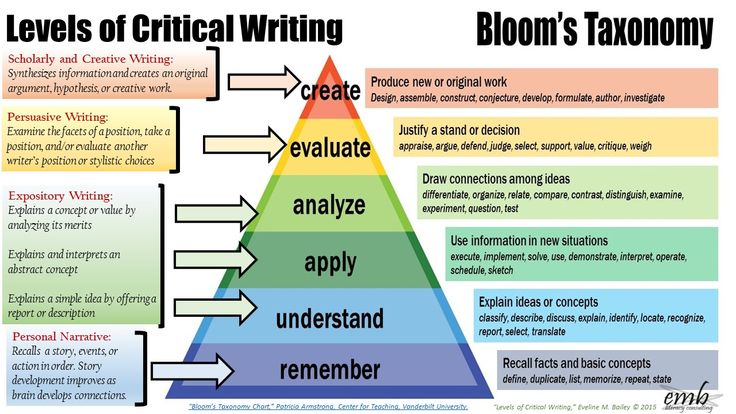
It is called the Fibonacci sequence - after the Italian mathematician of the 13th century. Defining the Fibonacci sequence recursively is very easy, but analytically it is very difficult. n -th Fibonacci number is expressed through its ordinal number by the following formula.
At first glance, the formula for n th Fibonacci number seems implausible, since the formula that specifies the sequence of only natural numbers contains square roots, but you can check the validity of this formula "manually" for the first few n .
Properties of number sequences.
A numerical sequence is a special case of a numerical function, so a number of properties of functions are also considered for sequences.
Definition . SECRECTION { Y N } is called increasing if each of its member (except the first) is more than the previous one:
1 Y 2 Y 3 Y N Y N N N N N N N N +1
Definition.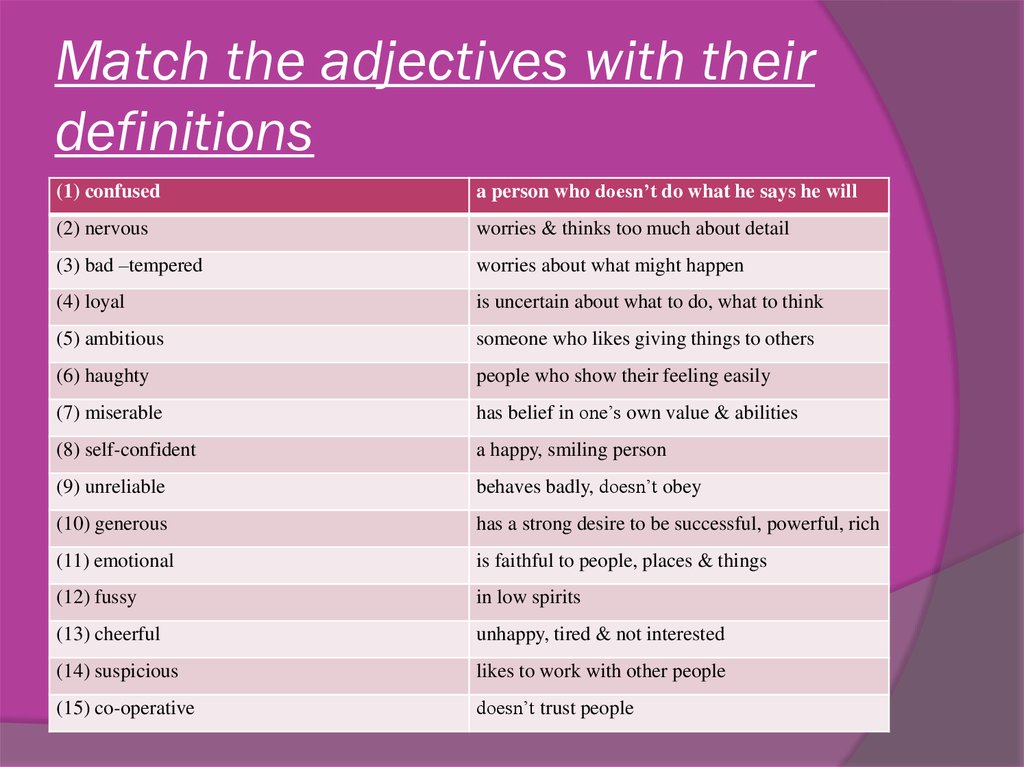
The sequence { y n } is called decreasing if each term (except the first) is less than the previous one:
Y 1 > Y 2 > Y 3 > ...> Y > Y N +1 > ... .
Increasing and decreasing sequences are united by a common term - monotonic sequences.
Example 1. y 1 = 1; y n = n 2 is an increasing sequence.
Example 2. y 1 = 1; is a descending sequence.
Example 3. y 1 = 1; – this sequence is not non-increasing non-decreasing.
Definition. A sequence is called periodic if there exists such a natural number T , that starting from some n y n = y n+T . The number T is called the length of the period.
Example. The sequence is periodic with period length T = 2.
Arithmetic progression.
A numerical sequence, each member of which, starting from the second, is equal to the sum of the previous member and the same number d , is called an arithmetic progression , and the number d is called the difference of an arithmetic progression.
Thus, an arithmetic progression is a numerical sequence { a N }, specified by the recurrent ratios
A 1 = A , A N = A N –1 + D ( N ( N ( N ( N ( N. , 4, …)
( a and d are given numbers).
Example. 1, 3, 5, 7, 9, 11, … is an increasing arithmetic progression, where a 1 = 1, d = 2.
Example. 20, 17, 14, 11, 8, 5, 2, -1, -4, .
.. - decreasing arithmetic progression, which has a 1 = 20, d = -3.
It is easy to find an explicit (formula) expression a n through n . The value of the next element increases by d compared to the previous one, so the value of the n element will increase by the value ( n – 1) d compared to the first member of the arithmetic progression, i.e.
a n = a 1 + d ( n - 1).
This is the formula of the n-th member of the arithmetic progression.
Using a clear expression A N through N , the following property of arithmetic progression can be proved: if the natural numbers I , J , K , L are the same as I + + + + + + + + + + = k + l , then a i + a j = a k + a l .
To verify this, it is enough to substitute i , j , k and l instead of n into the formula n- of the arithmetic progression member and add. It follows that if we consider the first n members of an arithmetic progression, then the sums of the members equally spaced from the ends will be the same:
a 1 + A N = A 2 + A N - 1 A 3 + A N -2 9 2 a 1 + ( n - 1) d .
The last equation allows you to calculate the sum of the first n terms of an arithmetic progression:
S n = a 1 + a 2 + … + a n –1 + a n .
for this purpose is taken by another same amount, but the terms are recorded in the reverse order:
S N = A N + A N - 1 + .
.. + ... + ... + ... + ... + ... + ... + ... a 2 + a 1 .
Further, it is added term by term with the original sum, and the terms are immediately grouped in pairs. As a result
2 S N = ( A 1 + A N ) + ( A 2 + A N –1 ) + ... ) + ... + ... + ... + ... + ... + ... + ... a n + a 1 ) = n (2 a 1 + ( n ), – 3) d 90. This is the formula for the sum of n members of an arithmetic progression.
The arithmetic progression is named because in it each term, except for the first, is equal to the arithmetic mean of the two adjacent to it - the previous and the next. Indeed, since
a n = a n –1 + d ;
a n = a n +1 - d .
Adding the last two equalities gives .
Thus, the following theorem is true (a characteristic property of an arithmetic progression). A numerical sequence is arithmetic if and only if each of its members, except for the first (and last in the case of a finite sequence), is equal to the arithmetic mean of the previous and subsequent members.
Example. At what value of x do the numbers 3 x + 2, 5 x - 4 and 11 x + 12 form a finite arithmetic progression?
According to the characteristic property, the given expressions must satisfy the relation
Solving this equation gives x = -5.5. With this value x given expressions 3 x + 2, 5 x - 4 and 11 x + 12 take the values -14.5, -31.5, -48.5, respectively. This is an arithmetic progression, its difference is -17.
Geometric progression.
A numerical sequence, all members of which are non-zero and each member of which, starting from the second, is obtained from the previous member by multiplying by the same number q , is called a geometric progression, and the number q - the denominator of a geometric progression.
Thus, geometric progression is a numerical sequence { b N }, specified as recurrent ratios
1 = b , b = b = b = b = b = b = b b. –1 q ( n = 2, 3, 4…).
( b and q - given numbers, b ≠ 0, q ≠ 0).
Example 1. 2, 6, 18, 54, … – increasing geometric progression b = 2, q = 3.
Example 2. 2, –2, 2, –2, … – geometric progression b = 2, q = -1.
Example 3. 8, 8, 8, 8, … - geometric progression b = 8. q = 1. > 1, and decreasing if b 1 > 0, 0 q
One of the obvious properties of a geometric progression is that if a sequence is a geometric progression, then the sequence of squares, i.e.
b 1 2 , b 2 2 , b 2 , .
.., b N 2, ... is geometric progresses, the first equals b 1 2 , and the denominator is q 2 .
Formula N- of a geometric progression member has a type
B N = B Q N- 1 .
You can get the formula for the sum of terms of a finite geometric progression.
Let a finite geometric progression be given0039 3 , …, b n
S N = B 1 + B 2 + B 3 + ... + B N .
It is assumed that q No. 1. To determine S n , an artificial technique is used: some geometric transformations of the expression S 9 are performed0039 n q .
Then
S N Q = ( B 1 + B 2 + B 3 + .
.. + B N + N ) q = b 2 + b 3 + b 4 + ... + b N + b N N N N N N N N 900 n + b n q - b 1 .
So S n q = S n + b n q – b 1 and therefore .
This is a formula with ummah n members of a geometric progression for the case when q ≠ 1.
When q = 1, the formula can not be derived separately, it is obvious that in this case S n = a 1 n .
Geometric progression is named because in it each member except the first one is equal to the geometric mean of the previous and subsequent members. Indeed, since
b n = b n- 1 q;
b N = b N+ 1 /Q,
, therefore, b N 2 N - 1 9 1 b n+ 1 and the following theorem (a characteristic property of a geometric progression) is true: finite sequence) is equal to the product of the previous and subsequent terms.
Sequence limit.
Let there be a sequence { c n } = {1/ n }. This sequence is called harmonic, since each of its members, starting from the second, is the harmonic mean between the previous and subsequent members. The geometric mean of the numbers a and b is the number , or . As n grows, all members of the geometric progression decrease and their value approaches zero. In this case, it is customary to say that as n tends to infinity, this sequence converges and zero is its limit is . It is written like this:
.
The strict definition of the limit is formulated as follows:
If there exists a number A such that for any (arbitrarily small) positive number ε there exists a natural number N (in general, depending on ε) such that for all n ≥ N the inequality | a n – A | { a n } converges and A is its limit.
It is designated as follows: .
Otherwise, the sequence is called divergent.
Based on this definition, one can, for example, prove the presence of the limit A = 0 for the harmonic sequence { c n } = {1/ n }. Let ε be an arbitrarily small positive number. The difference
is considered.
Does such a thing exist N that for all n ≥ N the inequality 1 /N ? If we take as N any natural number exceeding 1 /ε , then for all n ≥ N the inequality .
It is sometimes very difficult to prove the existence of a limit for a particular sequence. The most common sequences are well studied and are listed in reference books. There are important theorems that make it possible to conclude that a given sequence has a limit (and even calculate it) based on already studied sequences.
Theorem 1. If a sequence has a limit, then it is bounded.
Theorem 2. If a sequence is monotone and bounded, then it has a limit.
Theorem 3. If the sequence { a N } has a limit of A , then the sequence { CA }, { A N + C} and {| | | | a n |} have limits cA , A + c , | A | respectively (here c is an arbitrary number).
Theorem 4. If the sequences { a N } and { b N } have limits equal to A and b , qb n } has a limit of pA + qB .
Theorem 5. If sequences { a n } and { b n } have limits equal to A and B respectively, then the sequence { a n b n has a limit of 90 AB 016.
Theorem 6. If the sequences { a N } and { b N } are equal to A and b , ≠ 0 and B ≠ 0, then the sequence { a n / b n } has a limit of A/B .
Anna Chugainova
Numerical sequences: definition, formulas, limits of sequences
At the request of readers, we resume the section "Mathematics for Dummies". We are talking about number sequences and calculating their limits. We find out how the sequence differs from a simple set of numbers and how it can be specified.
Need more useful and interesting information? This goodness does not happen much! Join us on telegram.
Sequences of numbers
We encounter sequences of numbers every day. That's just a meeting with the sequences on the exam may not be the most pleasant.
To make it different, read this article, and if something is not clear, feel free to contact our consultants for help.
One of the most interesting and famous sequences is the Fibonacci numbers. This sequence has amazing properties and is often found in nature. For example, sunflower seeds are arranged in two spirals. The numbers indicating the number of seeds in each of them are members of the Fibonacci sequence.
What is a number sequence?
A sequence is a set of elements of a set that satisfies the following conditions:
- for every natural number there is an element of this set;
- this number is the element number and indicates the position of this element in the sequence;
- for any element of the sequence, you can specify the element following it.
Number sequence is a function of variable n , which belongs to the set of natural numbers N .
The existence of a function by which any member of the sequence can be calculated differs from a random set of numbers.
Words sound cumbersome and complicated. But that's what mathematics is for, to write everything in letters and numbers. Usually the sequence is denoted by the letter x, although others can be used.
What are the sequences
Distinguish:
- constant or monotonic sequence: 1, 1, 1, 1, 1.
..
- increasing sequence in which each next element is greater than the previous one
- a descending sequence in which each next element is less than the previous one
Sequences are also divided into convergent and divergent. A convergent sequence has a finite limit. And the limit of a divergent sequence is equal to infinity, or the sequence has no limit at all. But about the limits a little later.
Consider the most famous examples of sequences. Since school, everyone is familiar with arithmetic and geometric progressions.
Arithmetic progression
Let's look at the numbers:
What do they have in common? They are all odd and each next can be obtained from the previous one by adding the same number to it. Let's call it d . In this case, d = 2.
The sequence described above is an arithmetic progression. Here are the basic formulas for it:
The element a with the number n is called the common member of the sequence. And the number d is the difference of an arithmetic progression.
The sum of the first n terms of the progression is calculated by the formula:
Also, an arithmetic progression has a characteristic property:
Geometric progression
A geometric progression is a sequence of numbers, each member of which, starting from the second, is equal to the previous member multiplied by the same number q is the denominator of the progression. The elements of a geometric progression are given by the ratio:
The basic formulas for a geometric progression are given below. Formula N Progress:
The first N Progress members:
The characteristic property of geometric progress:
Ways to assign sequences
can be required by several ways:
- Analytically or, more simply, by formula.
- Recurrent. Here, the first few terms of the progression are known and there is a formula that allows you to calculate the subsequent ones.
- Descriptive, simply listing all elements of a sequence.
Sequence limit
We have already talked about the limits of functions and how to calculate them. It follows from the definition of a sequence that a sequence is a certain function. So, the calculation of the limits of sequences will be in many ways similar to the calculation of the limits of functions. True, with its own characteristics.
The limit of a sequence is an object to which the members of the sequence tend to grow as the ordinal number n increases.
Let's put it another way. This is the number in the neighborhood of which all the members of the sequence lie, starting from a certain number.
Variable n in sequences always tends to infinity, in the direction of increasing natural numbers.
Things to remember when calculating the limits of sequences
By the way! It's also good to remember that all of our readers are currently on discount 10% to any kind of work .
- A sequence can only have one limit.
- If the sequence has a limit, then it is limited. The reverse is not always true!
- If the terms of some sequence zn are enclosed between the corresponding terms of two sequences xn, yn converging to the same limit, then this sequence also converges to the same limit.
- Constant sequence limit is equal to its constant.
- If two sequences x and y are equal, then the limits of these sequences are also equal, if they exist.
- If each member of a convergent sequence does not exceed the corresponding member of another convergent sequence, then the limit of the first does not exceed the limit of the second.
- The limit of the sum (difference) of two sequences is equal to the sum (difference) of their limits. Provided that both sequences have limits.
- The limit of the product of two sequences with limits exists and is equal to the product of the limits of the sequences.
Learn more
