What math should a kindergartener know

Kindergarten math | GreatSchools.org

From the first moment they look at your cooing face, babies start trying to make sense of their new reality. They’re hungry, they cry, and food arrives. In its most rudimentary form, they’re learning the essence of mathematics: logical thinking and problem solving.

By the end of kindergarten math, your child should be able to:

years Count to 100 by ones (1, 2, 3..) and tens (10, 20, 30…).
Use objects, like blocks, to count, add, and subtract up to 10.
Identify circles, triangles, rectangles, and squares.
Sort items by size, shape, weight, and length.
Understand where things are located: The cat is behind you, the pirate is below deck, the rainbow is above your head, you are next to me, and the teacher is in front of the classroom.

“I can count to 100!”

Kids love to show you what they’ve learned, and there’s plenty to be proud of in kindergarten. Your child will learn to identify and write numbers from 0 to 20. Ask them to point to the number that shows how old they are. They’ll be able to count to 100 — the long way saying one number at a time — and the short way skipping from 10 to 20 to 30 and so on. They’ll answer questions like, “what’s after 73?” and “what’s the number before 15?” They’ll understand that the number 3 is bigger than the number 2 and that 49 is smaller than 50, which comes after it.

Giving and taking away

Kindergartners learn to add and subtract within 10, but not with a pencil and paper. They’ll use objects and drawings. If there are 7 toy cars in a pile on the floor and one is removed, how many are left in the pile? If Juan has 4 cookies and Michele has 2 cookies, how many cookies do they have together? It gets a bit more difficult when they’re asked how many more cookies would they need for a total of 9, but that’s okay, because that’s pretty advanced. Also, some kindergartners will understand the equations for addition and subtraction, such as 6 + 3 = 9, but it’s not essential this year.

Place value

In kindergarten, kids learn that numbers between 11 and 19 are made up of 10 plus some ones. They understand that 12 is the same as 10 and 2 more. Their teacher will use different objects to explain this, such as a giving students 16 beans and having them create one pile of 10 plus 6 individual beans. This is the first step on their path to understanding place value.

More or less

Children already see the world as things that are the same and things that are different. Kindergarten is a key year for measuring, classifying, and comparing, both developmentally and in math. Your child may sort her toys into groups of animals, board games, and trucks or arrange her stuffed animals from tallest to shortest. The good news is, when your child upends a dish full of seashells onto the floor to sort the pink ones from the white ones, you’ll now know he’s practicing important math skills.

Students learn to compare two objects by their length, weight, and size. Who’s taller, my best friend or me? Which is heavier, this hollow ball or this solid rock? Remember when your parents marked your height on the doorjamb every year so you could see how much you grew? If you’re not doing that now, go ahead and start. It’s a great learning tradition to continue with your children.

Shape shifting

Your kindergartner should learn to identify the four basic shapes: circles, triangles, squares, and rectangles. During the year, kids learn to differentiate triangles from rectangles, and rectangles from squares. They learn to sort shapes into groups according to their similarities and count how many there are in each group.

Kindergartners start learning to identify, draw, build, and sort some 2-dimensional and 3-dimensional shapes. For example, a circle drawn on paper is 2-dimensional (also known as flat), but you can hold and bounce a ball, which is a 3-dimensional sphere.

Where are you?

One of the most important concepts in kindergarten is following directions, such as put your lunch boxes inside your cubby, shoes go into the basket, put your painting next to Ida’s, and please stand behind John in line. These words are new to kindergartners. They indicate where thing are in space. Not only are they crucial for doing what the teacher asks, they’re also important for kindergarten math. Other words your child should learn sooner rather than later? Below, above, beside, in front, on top, and under.

Enjoy this time as your little one revels in counting, comparing, and shapes. Before you know it, they’ll be studying radian measures of angles traversed counterclockwise around a unit circle, and you’ll be longing to add and subtract with cookies.

Print out our favorite five math worksheets for kindergartners.

Math Skills for Kindergarten, What Your Child Will Learn, Komodo Math

Math Tips
Education
K

As your child heads into kindergarten, you’ll be feeling all sorts of emotions. You may be wondering: How can my baby be that old? Is she ready? What exactly is he going to learn in kindergarten?

While kindergarten may have changed since you were a child, it still forms the foundation of your child’s schooling and we wrote earlier about how to prepare for a successful start to the school adventure.

In math, students will learn the basics of how numbers work while exploring place value and the concepts of addition and subtraction.

But there’s no need to figure everything out as your child does - this article will help you get a head start by knowing what to expect.

In kindergarten your child will learn how to:

1. Count to 100

Going into the school year, your child may be able to orally count to 10 or beyond. By the end of kindergarten, expect that counting to advance to 100. But don’t worry, we’re only talking about counting orally. Your kindergartner will not be expected to write all the numbers to 100.

In most kindergarten classrooms, teachers count the days of school with the children. By counting each day, children gradually become more fluent with bigger and bigger numbers. At the end of 100 days, kindergarten classrooms often have a big celebration with many more opportunities for counting.

At home: To support your child’s counting skills, encourage your kindergartner to count as high as possible. This is a great task to give your child in the car - or even at bedtime!

2. Answer “how many?” questions about groups of objects

As well as counting to 100, kindergartners will be asked to count how many objects are in a group. Students need to be able to physically count objects one at a time, assigning one number to each object as they count. This is a skill called one-to-one correspondence.

At home: Ask children to tell you how many toys they are playing with and watch how they keep track of each object that is counted. If your kindergartner counts the same object twice or skips an object, encourage another try.

3. Solve basic addition and subtraction problems

In kindergarten, children start to develop an understanding of addition and subtraction within 10. Kindergartners start by solving problems involving physical objects, and as the year goes on, students learn to draw pictures to represent addition and subtraction problems. They will even begin to solve simple word problems.

At home: Present two groups of blocks (less than 10 in all) and have your child add the blocks together. As your child develops understanding, you can ask simple addition or subtraction problems without using the physical objects as a support.

4. Understand the numbers 11-19 as a ten plus some ones

Though it may seem quite advanced, your kindergartner will begin to understand the concept of place value and that position makes some numbers bigger than others - ie get to grips with the idea that 21 is bigger than 12. Students may use place value blocks to be able to “see” how ten ones become a ten.

At home: When counting blocks or lego bricks at home, make a group of ten. Then add on extra “ones” to make the numbers 11-19. You can even talk about place value when looking at written two-digit numbers.

5. Name shapes

Kindergartners will learn about 2D and 3D shapes. They should be able to name different shapes while describing their features. Kindergartners love to recognize shapes in the real world!

At home: Help your child by having them spot squares, cubes, spheres, rectangles, etc. Challenge your kindergartener to draw pictures using basic 2D shapes, then talk to you about the drawings. Making and continuing shape patterns is another fun way to help engage your kindergartner as they learn about shapes.

Throughout the year, make sure to ask your child about what’s happening in kindergarten math. Give your child an opportunity to teach you by sharing what he or she has learned. Get ready for a fun year in kindergarten!

Found this useful? Check out our grade by grade math guides from Kindergarten to 5th grade

Written by Lily Jones, Lily loves all things learning. She has been a kindergarten & first grade teacher, instructional coach, curriculum developer, and teacher trainer. She loves to look at the world with curiosity and inspire people of all ages to love learning. She lives in California with her husband, two kids, and a little dog.

About Komodo – Komodo is a fun and effective way to boost K-5 math skills. Designed for 5 to 11-year-olds to use in the home, Komodo uses a little and often approach to learning math (15 minutes, three to five times per week) that fits into the busy family routine. Komodo helps users develop fluency and confidence in math – without keeping them at the screen for long.

Find out more about Komodo and how it helps thousands of children each year do better at maths – you can even try Komodo for free.

Back to School - 5 Tips to Help you Ease Back into the Routine

Here are some steps you can take to ease children back from full vacation mode so that the first week of school doesn't knock you sideways.

Mindset - The Path to Mastery

People who have a growth mindset believe that they always have the potential to learn and improve. They are more motivated to persevere with difficult tasks, to take risks and to learn from failure.

Mathematics in grade 1 - what should a child be able to do?

Global development does not stand still, so the requirements for a person and his capabilities are constantly increasing. Including such a category of the population as schoolchildren. They need to work almost without rest in order to withstand the competition of their peers.

The level of knowledge of first graders has also become quite high. Schools do not have strict requirements for future students, but still, yesterday's kindergarteners must be prepared for basic subjects. It will be easier for a child to study in the first grade if he knows letters and sounds, can read by syllables, hold a pen correctly, and even better be able to write letters and know the alphabet well. As for mathematics in the first grade, there are also some requirements: you need to know simple geometric shapes, count up to 10, and preferably up to 20, understand what direct and reverse ordinal counting is, navigate on a sheet of paper. nine0003

Both the educational and moral readiness of children is important. Parents are worried about the future first-grader, because even knowing everything that is needed, he can get confused and nervous. And school interviews are held precisely for this, so that teachers can understand how capable and prepared the child is.

How can I help my child learn the school curriculum in mathematics in the first grade?

Many parents from the first grade strive to teach their children to study well - to get only A's. But at the same time, they forget to emphasize that the most important thing is to gain knowledge. Even first-graders often have a problem that the grades are good, but there is very little knowledge. After all, it’s easy to just memorize the material in order to answer well at the blackboard the next day. It is difficult to understand and understand the topic in order to fix it forever. nine0003

Therefore, parents should convey to their children that the most important thing is to understand mathematics, learn how to apply it in life, consciously perform exercises, not solve examples in the classroom mechanically, but only with full understanding and without haste. For conscious learning, the development of logic and non-standard critical thinking also helps. Thanks to them, it will be easier for the student to understand mathematics and apply its laws in life.

1st grade math assignments

First-graders' education is mainly based on what the children learned in pre-school lessons. The past is repeated, and the complication of the material occurs very gradually. nine0003

Mathematics assignments in grade 1 are the study of a straight line, a point, a broken line, simple geometric shapes, both written and mental counting. Considering that the basis of algebra is the multiplication table, then in the first grade there is preparation for its study: fundamental knowledge is gained, which in the second grade allows you to master the multiplication table.

In addition, of course, students learn to find figures in the world around them, broaden their horizons, try to apply in life the calculation that they have already mastered. They also solve puzzles, puzzles, easy entertaining tasks, the simplest examples. Despite the fact that this is a school, teachers try to teach the material in an interesting way, and pick up tasks that are exciting and in a playful way. nine0003

Math puzzles and quick wits

In addition to learning numbers, rules and counting, it is important to give your child to solve various puzzles and puzzles. It is non-standard tasks that help a child develop his brain, learn how to find a solution, are not afraid of difficulties, apply mathematical tricks. Simple examples will only help to work out the skill of arithmetic calculations, and you can develop further only using non-standard thinking.

The modern Amamatika method from the AMAKids Intelligence Development Academy includes an online platform and math game simulators that allow you to develop all the abilities of children in the field of mathematics at once.

In order to teach students to easily solve problems of any complexity, as well as apply the “queen of sciences” in life, our textbooks and manuals offer interesting tasks with missing numbers, unbroken crosswords and puzzles, mathematical puzzles for grade 1 and for older children, fascinating mazes , tasks for ingenuity. Knowing how to apply non-standard methods of solving, the child does not experience fear of tasks of increased complexity. He takes on any challenge with interest. nine0003

Math Simulator Grade 1

The Amamatika platform and simulator will help you not only succeed in school, but also teach you how to find an approach to complex tasks, teach financial literacy and the basics of programming, help develop analytical thinking, spatial imagination. Mathematics is a complex subject, but if you approach learning in a structured way and adhere to a proven methodology, a student will be able to understand and consolidate even the most difficult topics.

On our convenient online platform, students can pull up any mathematical direction - you just need to go to the required section and start doing the exercises. The first grade math simulator will provide a correct understanding of the subject and lay the necessary foundations for further learning.

Also on the gaming platform there are sections with arithmetic, geometry, tasks, as well as tasks on financial literacy, programming and games for the development of logic, memory and attention. Amamatika - effective and convenient courses for modern children. nine0003

“How I fell in love with mathematics with all my humanitarian soul”

These thoughts have been tormenting me ever since I started teaching mathematics. And at one fine moment (he was really beautiful) I realized that I fell in love with this subject with all my non-mathematical soul. It turned out that everything is determined by the environment and the correct teaching methodology.

Since childhood, I have experienced a persistent hatred for this, as it seemed to me, far-fetched and senseless discipline. No, I did not dispute the fact that mathematics is vital and that people cannot do without it. But it is available only to some certain class, or even, perhaps, to some special breed of people, whose brain probably consists of some other substance than mine. nine0003

After graduating from school and having passed the exam with grief in half, I was glad, my dear, that I would never have to suffer from this "nonsense" again. How wrong I was then. But I was even more wrong when I thought that I would hate the Queen of Sciences all my life.

Everything went according to a well-known scenario. Parents are musicians, there are no mathematicians in the family. What's the math there? The brain is not mathematical and other nonsense common in the school environment. We choked on such prejudices in childhood, retraining left-handers, “healing” stutterers with fear, and diligently sorting children’s brains into “mathematical” and “humanitarian”. nine0003

Observational tendencies with subsequent deductions made me deeply doubt my genetic genius. Yes, it is true that in a family of musicians, most likely, a successor to a musical dynasty will grow up, in a family of artists, the probability of the birth of an artist is very high, and in a family of mathematicians, it is quite possible that a child with a mathematical mindset is growing up.

And the easiest thing to do in this matter is to blame everything on genes. They are so tiny. Maybe it's true. But life has made me repeatedly convinced of something else. The decisive role in the orientation of the personality is played by the environment, the information field that surrounds the child from birth. What will he see, what will be surrounded by a newborn baby in the artist's family? What will adults talk about when they are next to him? And in a family of musicians, where music, the voice of a mother or father sounds more often than simple speech? What will the son of a mathematician meet when he reaches the bookshelves or the desktop? Books, numbers, formulas. Silent, but exuding an extraordinary and truly magical information field. I do not deny at all that something in the genetic information is different. Let geneticists deal with this. I am talking about what I observe in life. nine0003

So, the first thought: there are no "physicists" and "lyricists". There are no "mathematical" and "humanitarian" brains, but there is an environment that determines everything. But why then is mathematics so categorically difficult, incomprehensible and inaccessible to such a large number of students in school (almost more than half)?

Second thought: mathematics is not taught in school. Or in another way: what they pass off as mathematics is not mathematics. In the same way, in most schools, English lessons are far from the language itself, and singing lessons from music. nine0003

In all the years of schooling, I never managed to meet a mathematics teacher at school who was truly passionate about his subject and sincerely loved her. Therefore, I myself could not understand, accept, or love mathematics. There was no one at school to show me the true beauty of this science.

To serve ten years at a school desk and never see mathematics!

Instead, the teachers, conscientiously fulfilling their role, slipped me some kind of small change consisting of dry numbers, graphs and formulas, the essence of which they most likely did not understand themselves. The whole point of training was to come to the correct decision by given instructions by all means and pass the next test. I, who was born in a family of musicians, had no idea what relation to life all these graphs of functions and boats came out towards each other at the same speed. nine0003

The fact that mathematics is an art, as beautiful, diverse and multifaceted as music, sculpture or architecture, was not even known to the teachers themselves. In the school environment, mathematics is a common subject that must be passed. Passed means your brain is "mathematical", go to a technical university. Didn't pass - then you are a "humanist", and go to the musicians or study philology.

If until recently I felt it somewhere at the level of intuition, then after reading P. Lockhard's article "The Lament of a Mathematician" I just threw up my hands. Here is the explanation of the problem. Here is the answer to the question. nine0003

It's not that my brain is arranged differently, but teaching is going in the wrong way

And now, the third thought. Mathematics is best taught by ... non-professionals.
Do you remember the sayings: “If you want to know a subject perfectly, start teaching it” and “When you teach others, you learn yourself”? Consequently, only that knowledge is considered to be mastered, which was passed through itself, carefully comprehended and voiced.

In progressive educational circles today, the idea of the productivity of education is sounding more and more vividly, when the educational process is built in such a way that the student independently systematizes information in a way convenient for him and then (this is indispensable) tries to transfer this information to another. At the same time, it is quite natural that the teacher in this case is physically unable to possess the amount of knowledge of a graduate of the Faculty of Mathematics. It is enough that at the moment he is well oriented in that area of the system that he has realized. And if there is an adult in the place of the teacher: mom, dad, grandmother, who are poorly versed in mathematics? nine0003

Let's analyze how the whole learning process happens in this case. So, the story of one mother, who in childhood did not know mathematics well, but becoming a parent became so bold that, rejecting the help of the school and tutors, she took upon herself the responsibility of teaching her child mathematics on her own. I must say right away that at the time my eldest son entered the first grade, I already felt that teaching (not only mathematics, but in general) in elementary school was turned upside down. N. Zaitsev’s methods reliably protected my motherhood and the elementary school period in my son’s education and for many years brought up a special way of pedagogical thinking in my head. In other words, in teaching mathematics “according to Zaitsev”, the main thing is to read the manuals thoughtfully and not deviate from the course. Thus, we will not only qualitatively study the material in mathematics for elementary school, but also lay a solid foundation for subsequent work in high school. nine0003

How exactly (from my own experience) does mathematics “according to Zaitsev” differ from school mathematics? More on that just a few lines later. Meanwhile, the son goes to the sixth grade. The materials developed by N. Zaitsev are running out of stock. There comes a time of confusion. Once again I face the fact that I don't know mathematics. I don't know what to teach, nor HOW to teach. Go to school? Give up? Hire a tutor? But an inner voice convinces of the meaninglessness: “There is no mathematics there. It's useless to go there." nine0003

But where can I get it? The same article by P. Lockhart prompted the idea that mathematics should be taken from life itself. What surrounds us, how the space around us is organized, according to what laws it exists - this is mathematics, and not boring numbers on the pages of textbooks.

And now what was promised: what is the difference between mathematics "according to Zaitsev" from the corresponding discipline at school and from the mysterious "formation of mathematical representations" in kindergarten programs. In Zaitsev's methods, mathematics is a special organization of space, communication with which is built into ordinary children's life. nine0003

Mathematics for a child is life

Moreover, the meeting with mathematics begins not from a school desk or from a school preparation club and not even from a kindergarten preparatory group, but from the moment when the baby becomes able to contemplate the environment peace. Even then, while still at the level of feelings and sensations, he will know how a circle differs from a square and a triangle, long from short, wide from narrow, large from small. All concepts - angles, figures, areas, perimeters, fractions, sectors, lengths and sizes - are materialized, tangible and understandable. Zaitsev made mathematics visual and accessible to kids of a very early age, and, learning to look for and find it around him, he will continue to look for it all his life. nine0003

This is the discovery. Teaching mathematics must begin with the search for mathematics around us! It is necessary to teach the children to admire its beauty and grace. Mathematics, contrary to all established ideas, does not begin with numbers and counting.

Where does mathematics live? Just not in school textbooks. Today, with my four-year-old daughters, I began to study (no, no, to search) mathematics around us. We glue the application. House: a square and a triangle - well, what's wrong with that? How about cutting a square diagonally? You get two triangles. This is “what is it” for you, but for a child it is a discovery. Carefully cut off the corners of the rectangle and - hocus pocus - got an oval. And how to get a circle from a square? After such "tricks" it will be easier to talk with children about inscribed and described figures. nine0003

Did it ever occur to you that the game "Battleship" is the theme "Coordinate Plane" from the textbook for the sixth grade? And chess, by the way, too. We remember the basic principle "from visual-effective to verbal-logical", and not vice versa. Let us first give the child a clear concept of where this occurs in life and how, with the help of this knowledge, he can influence the world around him.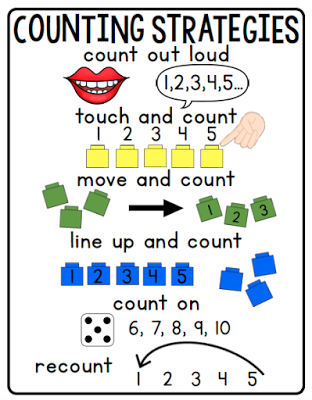

No one here refutes the classical mathematical theory. But every great scientist first realized his discovery by experience, and then only clothed it in beautiful words. The trouble is that many of our teachers and academicians, alas, have bypassed this experimental path. They were thrown axioms and theorems like a stale crust, which they continue to chew dry, now, together with their students, not feeling either taste or aroma. nine0003

In mathematics lessons, it is necessary to resurrect and bring to the fore everything that is considered far optional in school curricula.

N. Zaitsev, in methodological accompaniments to his manuals, offers a lot of ideas for organizing such activities with children: they are simply replete with mathematical tricks, rebuses, puzzles and tasks, sometimes so original and entertaining that to deal with them without the help of an adult, a student, rather can't do everything.

The purpose of such work according to Zaitsev is to awaken thought, ingenuity, imagination, without which it is impossible to solve any vital task, educational or creative

Mastering counting skills in such an educational process is not an end in itself, but an intermediate link, a logical obstacle that is necessary overcome to solve specific problems. The child initially sees the final result of his efforts: "I want to know, decide, guess."

It turns out that the whole process of teaching mathematics should be built the other way around: first, the patterns and features of the organization of the space around us, observation of changes, movement, time. And only after that we study how these changes and laws are reflected in mathematics. We study the numbers of the first hundred, discussing the age of parents and relatives, the multiplication table - through the area of a rectangle, the basics of geometry - through visual and effective work with the details of "Ornament". nine0003

We open a problem, we cannot solve it, we reach a dead end (oh horror) and start to analyze what laws and concepts we do not know, what relations between objects we have never paid attention to! To learn mathematics, you need to start interacting with mathematics. The same thing happens in language learning. In order to recognize the great and powerful, you need to read the great texts, quote and rewrite them, sorting out those unshakable, historically established principles on which the language rests, word by word, and not study stamped exercises from semi-literate school textbooks, which sometimes put forward very dubious versions about the true structure of the language. nine0003

When teaching children mathematics, it is necessary to monitor the quality of the material we offer them for study and observation.

And yet. How to teach a child mathematics in the conditions of family education, when the teacher himself is not too confident in his knowledge of the subject? In elementary school, the answer is clear: children learn quite successfully and easily according to the method of N. Zaitsev. So what is next? The answer is in the word "together".

Ignorance of mathematics does not relieve me of responsibility for my child's knowledge

If you don't see, look. If you don't know - learn. And together we search, draw, subtract, peer, look for analogies. Does not work? Ask for help. But this help does not consist in ready-made solutions and answers in the style: "Here you need to do this." The concept is not realized, the solution of the problem is not given into the hands. We are not looking for a tutor who, for a certain amount, with omniscient intonations, will lay out a dry instruction or formula for us. We try to "live" mathematics, to feel the right answer. Mathematics needs to be experienced. nine0003

Let's think: what is the point of teaching mathematics? Learn to count? This is the limit of elementary school. So what is next? Watching the processes taking place today in secondary schools, and remembering your school childhood, you realize more and more clearly that the goal of schooling in mathematics is to prepare for the Unified State Examination. Meanwhile, every adult who takes responsibility for teaching children mathematics should understand that the essence of this process is the disclosure of the potential capabilities of children's intellect, the development of all mental processes (thinking, memory, imagination, attention), the formation of the ability to set a learning task and independently select the means to solve it. nine0003

Successfully passing the USE is very important, but this is not what makes a person happy

USE is not life, it is just a separate short-term episode.