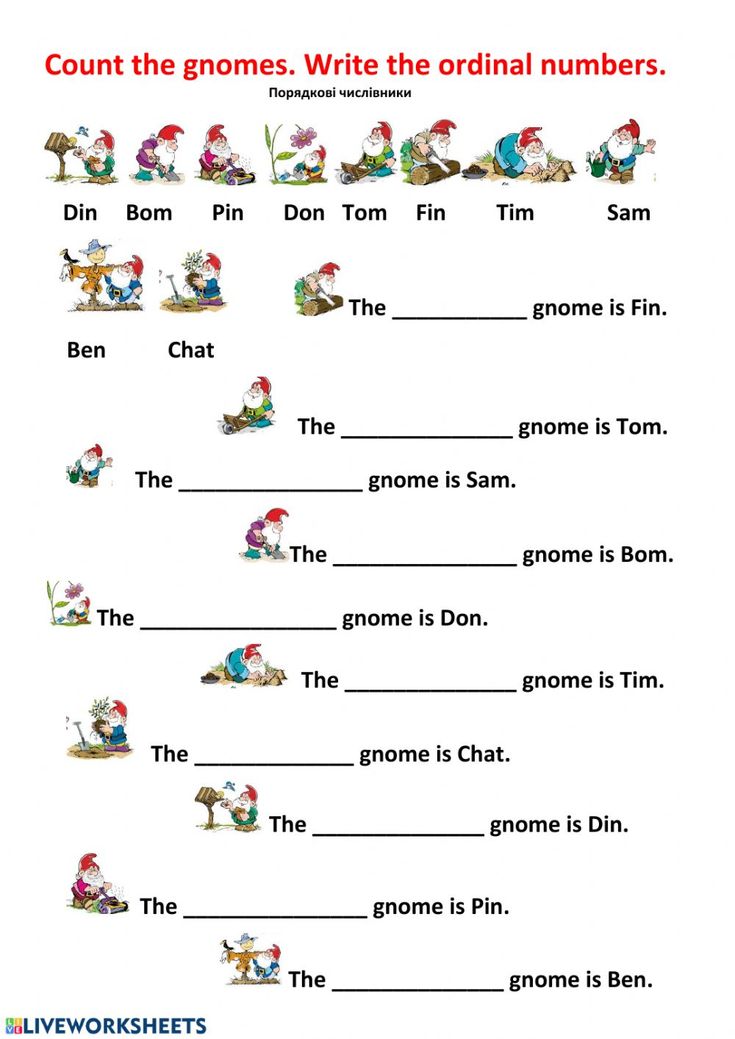
Activities for ordinal numbers

Activities For Ordinal Numbers | EnglishClub

Ordinal numbers can involve pronunciation problems like consonant clusters, syllables added or not (e.g. to 13th and 30th) and pronouncing th, and can also be used as a way of introducing those pronunciation points. In addition, students have to remember the forms. Most of the following activities for practising ordinal numbers are suitable for both adults and young learners.

1. Guess Your Position

Tell students how you are going to ask them to line up in a couple of minutes (e.g. by date of birth, date of their birthday, height, shoe size, number of brothers and sisters, number of times they have been to Disneyland, how long they have spent abroad in their life), and ask each student to guess where they will be in that line, e.g. “I think I will be (joint) third.” They then ask each other the question to find out that information (e.g. “When is your birthday?”), line up in that order, and get points if they are in the position they said they would be.

2. Ordinals Buzz Fizz

Buzz Fizz is a common numbers game that even native speakers play and find fun, and it can be played with ordinal numbers as easily as with cardinal numbers. Students take turns counting up one number at a time, but instead of any multiple of three they have to say “Buzz”, so going around the class or a group you get “First” “Second” “Buzz” “Fourth” “Fifth” “Buzz” “Seventh” etc. People who make a mistake can be made to sit out that round if you like. Once they have got the hang of that, you can also add “Fizz” for all multiples of five, making fifteenth, thirtieth etc “Buzz fizz”.

3. All Kinds Of Counting

An easier counting game is to get students to count up in different steps, starting with just “First” “Second” “Third” etc and then going to steps of two, three, five, ten etc.

4. Awareness Of Rank

Get students to guess the position of things in world or local rankings, e.g. “Where is the Thames in a list of Europe’s longest rivers?” This takes quite a lot of research, but if you have access to computers with the internet in class students can research and make the questions for each other.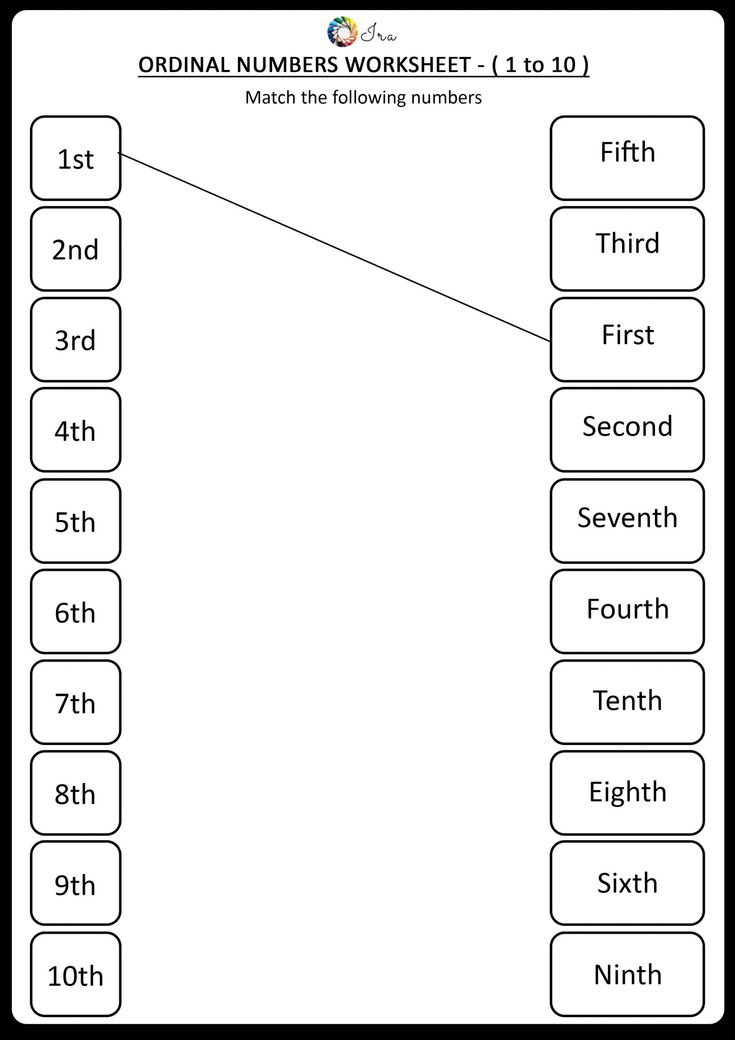

5. Rank Trumps

Produce a set of cards with a category of things that are similar to each other, e.g. one famous building on each. Each card should have some appropriate data about those things on it, e.g. speed and acceleration for cars or number of young and average lifespan for animals. Split the students into groups of between three and five and give them three or four cards each. One student should choose one of the pieces of data and say its name, e.g. “Height”. Each student should then guess where one of their cards could go in a ranking of all the cards in their group, e.g. “I think this card here will be first.” They then tell each other all the information and check the positions of the cards they chose, getting one point for each correct guess. This can also be played as a team game with between three and five cards per team.

6. Which Time?

The teacher or a student does the same thing many times, with one time being subtly different. The other students then say which time they think was different, e.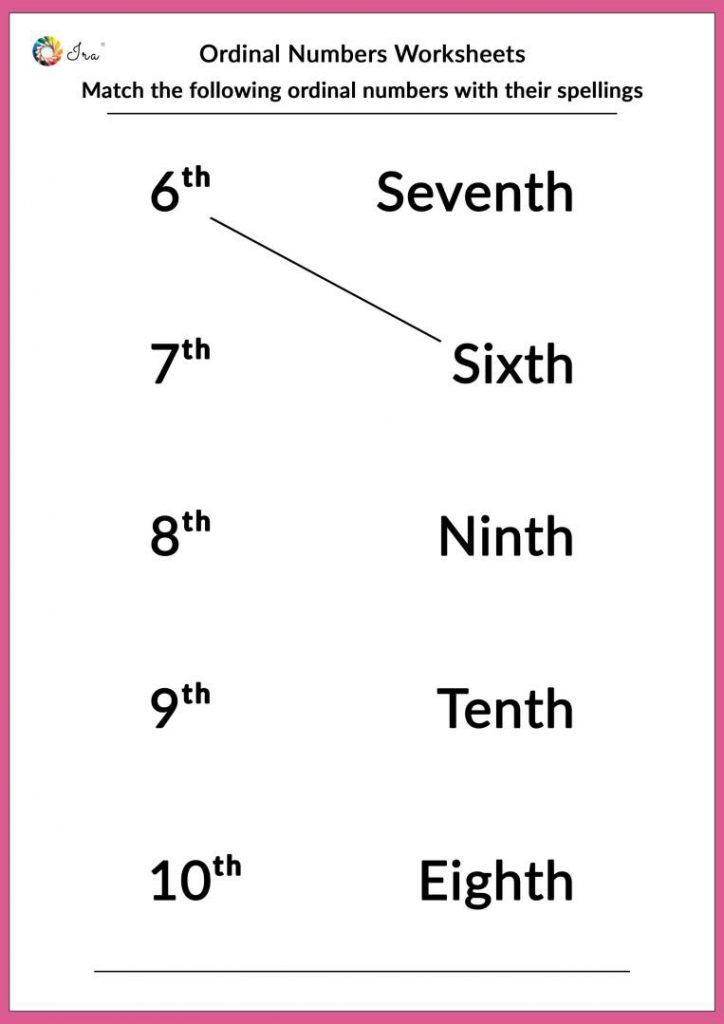 g. “The tenth time was ‘sheet’ instead of ‘seat’”, “The sixth time you said ‘Can I help you?’ wasn’t polite” or “The sixth word wasn’t a vegetable”. As with these examples, this works well for pronunciation points and lexical sets.

7. Instant Sequences

Students are asked a question about where in a well-known sequence someone or something is and race to say the right ordinal number, e.g. “Which position is February in months/Bill Clinton in the Presidents of the United States/‘Thou shalt not kill’ in the Ten Commandments?”

8. Ordering Ordinals Storytime

Give students between 10 and 20 cards with pictures or vocabulary on that they can use to tell a story. They work in pairs to decide on a story and put the cards in order, then change pairs and tell their stories one picture at a time to someone else. After each sentence, that person has to guess which picture the person telling the story put at that point and tell them using ordinal numbers, e.g. “I think this was your fifth picture”.

Definition And Activities For Kids

Learning mathematical skills is a vital part of early childhood development. And understanding ordinal numbers and how they work is part of building this competency.

Before we dive deeper into what ordinal numbers are and how you can assist your child with learning them, it’s important to know that we use them in our everyday lives.

This means your child has probably already come across this numerical concept, even though they may not know how to put it into words yet.

To help your young learner reach a stage where they fully comprehend and can use these numbers correctly, we’ve prepared five effective activities for you to try at home.

Let’s begin!

What Are Ordinal Numbers?

Ordinal numbers help us communicate the order of objects in a series. For example, first, second, third, and so on.

In theory, this sounds easy, but explaining it to children can be a little challenging. For instance, you can show a child the number “2,” and they may be able to understand what it means to have two of something (e. g., two eyes, two ears).

But when we talk about ordinal numbers, second (the ordinal number) is very different from two (the integer).

That’s because these numbers are not just about counting — they are more about things in relation to one another. And we have to look at a whole series or set for us to determine which object is first, second, third, etc.

The good news? Most children come across these types of numbers when watching a race or playing a game. They may be able to say:

Tommy came first.
Suzi was second.
Lorna was third.
Mike was last.

Children also spend a lot of time working with ordinal numbers in their early years at school because they connect with other critical mathematical concepts, such as sequencing and counting. So, helping your child understand them is part of a good foundation.

How Do You Write Them?

There are many different ways to write numbers, depending on what you are trying to show or solve.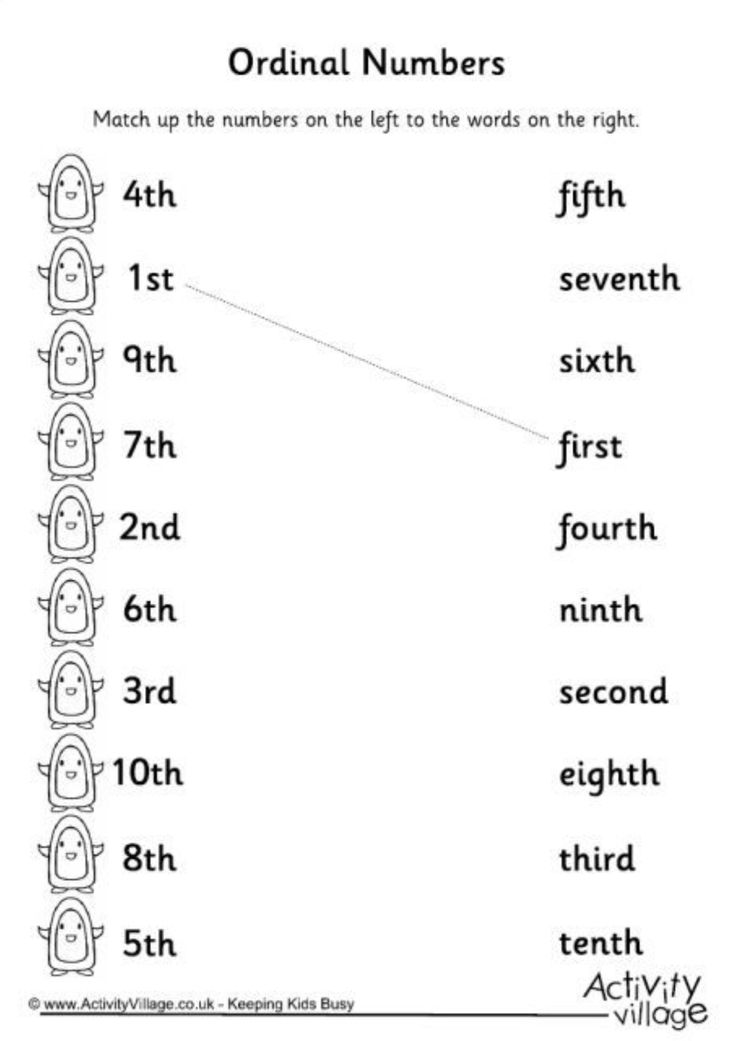 In the case of ordinal numbers, here are a few things to consider.

Let’s take a look at the first 10 ordinal numbers:

• First (1st)
• Second (2nd)
• Third (3rd)
• Fourth (4th)
• Fifth (5th)
• Sixth (6th)
• Seventh (7th)
• Eighth (8th)
• Ninth (9th)
• Tenth (10th)

From the above list, you can see that we write ordinal numbers by using the last two letters of the word. For example, fifth = 5th.

When looking at compound numbers, we apply the following:

• Numbers ending with 1: Only add “st” (e.g., twenty-first = 21st, thirty-first = 31st)
• Numbers ending with 2: Only add “nd” (e.g., twenty-second = 22nd, thirty-second = 32nd)
• Numbers ending with 3: o/Only add “rd” (e.g., twenty-third = 23rd, thirty-third = 33rd)
• Numbers ending with 4, 5, 6, 7, 8, 9, or 0: Only add “th” (e.g., twenty-fourth = 24th, thirty-fifth = 35th)

Some people add “ly” at the end of an ordinal number when it’s written out (e. g., firstly, secondly, thirdly, etc.). However, when dealing with larger numbers (from 9th upwards), it’s best to avoid the “ly” altogether.

Ordinal Vs. Cardinal Numbers

We can’t look at ordinal numbers without also identifying what cardinal numbers are and how they relate.

In a nutshell, cardinal numbers tell us how many there are of something. For example, you have two ears. We also use these numbers for counting. Ordinal numbers, on the other hand, tell us the order of things in a set. For example, Timothy is second in the line.

Distinguishing between these two concepts can sometimes be tricky, especially for young learners. For instance, they might say, “The number three question was so easy,” instead of, “The third question was so easy.”

Activities are a great way to help our children identify the differences between these two concepts. With that in mind, here’s our list of five fun and effective games you can play with your child at home!

5 Activities To Learn Ordinal Numbers For Kids

1) Toy Lineup

What You’ll Need:

• Index cards
• Marker
• Any toys of your choice

What To Do:

The simplest way to introduce ordinal numbers to children is by placing some of their favorite toys in a line.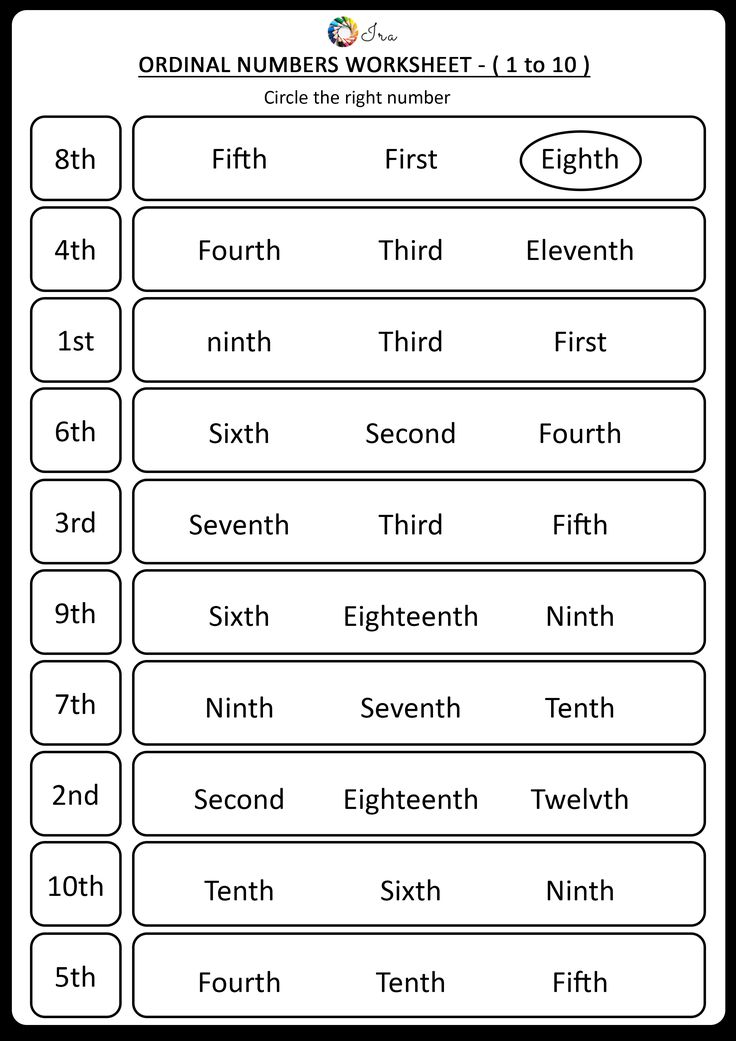

For this activity, you can use anything — dolls, toy cars, trains, legos — basically, anything you have an abundance of. After placing these items in a line, write ordinal numbers on your index cards (one number on each card).

To start playing, hand your child the index cards. Then, have them match the correct number card with each toy. For example, if they point at the fourth toy, they need to show you the card labeled “4th.”

You can start with just three to five items and, as they improve their skills, increase the line to 10 items or more.

This is a great way for children to get comfortable with what ordinal numbers look like in their numerical form.

2) Change The Lineup

What You’ll Need:

• Index cards
• Marker
• Any toy of your choice

What To Do:

As the name suggests, this activity is all about changing the positions of your lined-up objects. You can use the same toys you used in the previous game.

Start with changing the position of one object. For example, move one item from the third to the last spot. Then, ask your child:

Which toy is third in line now?
Which toy is last in line now?

Continue moving just one object at a time, and encourage your child to re-evaluate their positions.

This game allows children to grasp that just one change is enough to influence the whole series. It also encourages them to think beyond memorization. As you switch things up, they’ll have to focus on which object is now the first, second, third, and so on.

3) Story Plot Map

What You’ll Need:

• A sheet of paper
• Marker

What To Do:

To begin, draw four boxes on your sheet of paper and label them with ordinal numbers (1st, 2nd, 3rd, and 4th). Next, tell a story in parts. For example, it might look something like this:

First, a girl named Emily wanted to get a cat.
Second, she went to a store and found the cutest little kitty.
Third, she asked her parents to get the cat.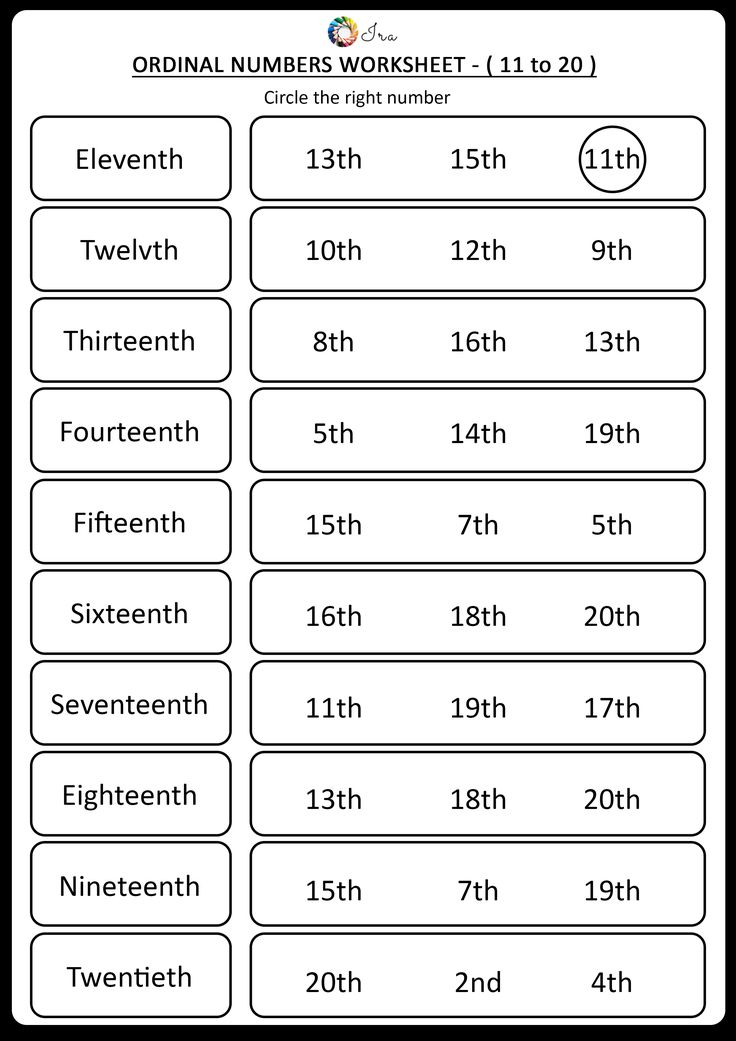
Fourth, they told her…

You can also write (or help your child write) what happens in each box as you tell the story. (So, “First, a girl named Emily wanted to get a cat” would go in the box labeled “1st”).

Point to each box as you tell that part of the story to give a visual representation of the events and emphasize the ordinal numbers (e.g., first, second, and so on).

Your story can take any direction you wish, and you can also encourage your child to give their input on what happens next.

One challenge with this game is ending the story on the last box. If there are four boxes, for example, then the fourth has to end it all. We recommend beginning by modeling all four boxes yourself first.

After that, your child thinks of box one, you get box two, they get box three, and you conclude the story for box four. After trying this a few times, let your child try the fourth box.

4) Color The Rainbow

What You’ll Need:

• White sheet of paper
• Pencil
• Crayons

What To Do:

Start by drawing eight lines in the shape of a rainbow on your sheet of paper.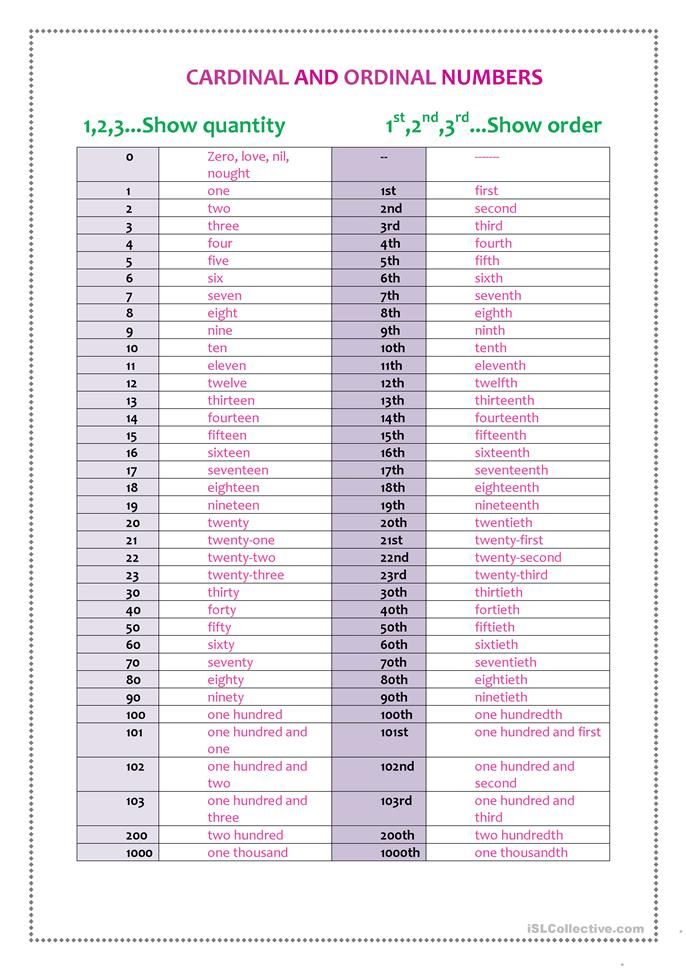 Then, hand the paper to your child. To play, have them listen to and follow directions as you tell them which stripe to color in.

For example:

Color the third stripe green.
Color the fifth stripe orange.

Continue giving instructions until the rainbow has all of its seven colors.

Don’t be surprised if your child has to count each time they color in a stripe. This is all part of practicing and learning as they go, and this activity reinforces that ordinal numbers are about looking at the order of a whole set.

5) Wrong Order

What You’ll Need:

• Index cards
• Marker

What To Do:

Start by writing 1st-10th down on your index cards (one number on each card). Then, shuffle the cards and line them up in the wrong order. Very simply, the object of the game is for your child to place the cards in the correct order.

They might need a little help in the beginning, but as they get more comfortable, you can add a timer to keep things interesting: Let’s see if you can line these up in their correct order in under 30 seconds!

This is a great activity for children to practice identifying ordinal numbers in their numerical form (1st, 2nd, 3rd, etc. ).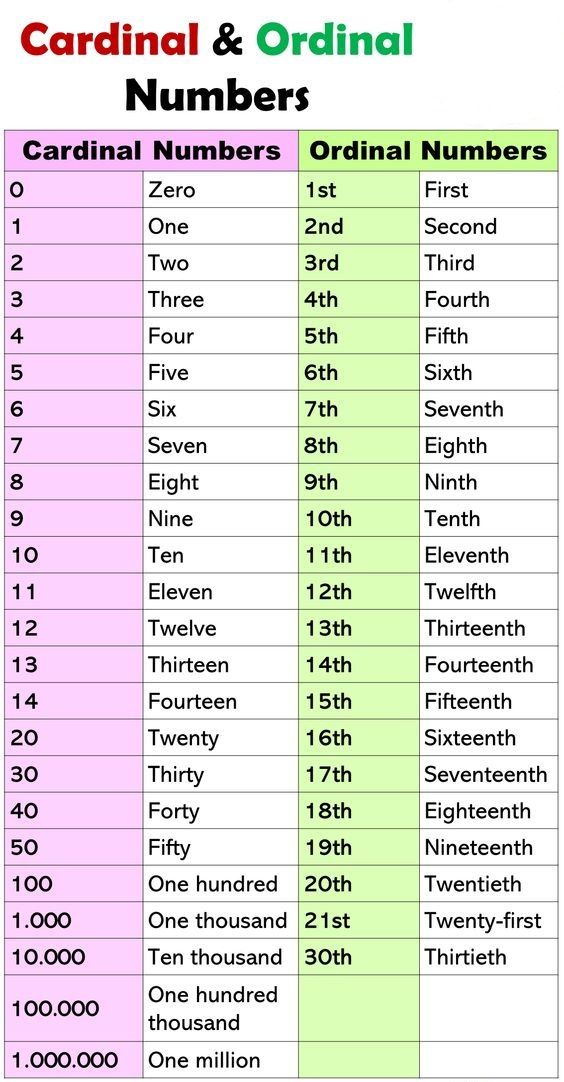

Ordinal Numbers Are Not So Ordinary!

While we may use the concept and language of ordinal numbers every day, there’s nothing ordinary about them.

And as you can now see, helping children learn to correctly identify these numbers is crucial because they form part of other important concepts, such as sequencing. The above activities allow your child to work on and solidify their knowledge of ordinal numbers with you at home.

In addition, our Wacky Slide game from the HOMER Learn & Grow app is specially designed to help reinforce the fundamentals of understanding and working with ordinal numbers.

By using these activities — and with lots of time and practice — your young learner will be an ordinal number pro in no time!

Author

Number Sequences - Umskul Tutorial

• How do we get used to sequences throughout our lives?
• What is the golden ratio?

What does it mean to “act consistently”? We do something according to certain principles, we do not break the rules. All our actions will have logic that we can track. In mathematics, it is also possible to arrange numbers in a strict order. Such rows will be called sequences.

Let's look at several series of numbers and reason.

What is the principle of the series of numbers 1, 2, 3, 4, 5, etc.? It's simple: add one to each new number.

And what is the principle in the series of numbers 2, 4, 6, 8, etc.? Here 2 is added to each new number.

What can be said about the series 2, 4, 8, 16, 32, etc.? Each new number is multiplied by 2.

All of the above series of numbers will be called sequence . How to describe it in one term?

Let's briefly recall the functions of numbers. Let's analyze the function f(x)=x+1.
If x = 0, then f(x) = 1.
If x = 1, then f(x) = 2.
If x = 2, then f(x) = 3.
If x = 3, then f (x) = 4.

Let's take a closer look at the function values ​​ : this will be our first sequence 1, 2, 3, 4, 5. We can conclude that the sequence can be specified using the function.

In fact, any sequence is a function. Now let's give a definition.

Sequence — a function defined on the set of natural numbers or its part.

That is, can be substituted into such a function only natural numbers.

More details about the function, its value, scope and other properties can be found in the article "Definition and Graph of a Function".

Argument will be is the serial number of the number in the sequence. The first number in the sequence will be given x = 1, the second number x = 2, the n number as x = n.

The numbers that form the sequence, - are the members of the sequence. And each member of the sequence has its own serial number.

How are the members of a sequence designated? We will not write every time “the twentieth term of the sequence” or something like that?

Sequence members have their own notation: an, where the index is after the letter and denotes the ordinal number of the sequence member.

for example,

• A ₁ - The first member of the sequence,
• A ₂₀ - twentieth member of the sequence,
• - , , , , , , , , , , , hundredth member of the sequence, and so on.