Home » Misc » Hands on activity for maths

Hands on activity for maths


7 Classroom Math Activities That Will Make Math Engaging and Fun

Back to Articles

Fun, hands‑on math games are a great way to make early math concepts clear and keep your students engaged.

Introducing math games into the classroom is a great way to make learning fun, engaging and motivating for young learners.

And the best part about starting early (kindergarten to grade 2) is that it helps your students to develop a positive attitude toward math from an early age, setting them up for a successful academic future.

Here are some fun classroom math activities that will have your students begging to do more.

Math Bingo

This math game is sure to become a fast favorite with your students. You can choose whatever skill you want to review, such as addition, subtraction, or number sequencing. The game works just like regular bingo, except students have to solve math problems in order to know what number to mark off of their sheet.

To prepare, make a list of 25 math problems (e.g. 2+1, 3–0, or 2, 4, 6, _ ). Write the answers on the same sheet of paper.

Create your own 5x5 bingo cards or generate them online. At random, write the answers on the cards using the solutions from your list. There should be a bingo card for each student playing. You can laminate the cards to use for next time and have students place pennies or rocks to mark their answers.

Make a paper plate clock

Are your students learning to tell time this year? This hands‑on craft activity is a fantastic way to practice this important skill.

Start with a paper plate and make a small hole at the center. Students should write the numbers in the correct places. Using colored paper, they can then cut the clock hands to the right size and secure them using a split pin from the center. You can even use a second plate (different color) for students to write the minutes. Glue the second plate to the bottom of the first so that it creates a rim.

Guess the weight

Children love playing guessing games, and when it comes to whether something is heavy or light, there can certainly be a few surprises in store for them.

Gather several items and spread them across a table. One at a time, ask students to guess the weight of each item and write their predictions in one column on a page (you can create a simple template for this too). Using kitchen scales, invite individual students to weigh each item and record the correct answers in a second column. You can also add a column in between and pass each item around the class, so students can guess the weight after holding each in their hand.

Hopscotch math

This game is a great way to get your students outside on a nice sunny day. Using a piece of chalk, draw a hopscotch grid on the pavement mimicking a calculator layout. Ask students to form a line and one by one, give them a simple operation (e.g. 2+3, 5–0). Students should take turns hopping on each element of the equation in the correct order, landing finally on the answer.

In another game, you can call out a number and ask students to hop on any equation that equals to that number. For a fun twist, ask students to hop on one leg for odd numbers, and two legs for even numbers.

Hopscotch math is a fun activity which helps students to practice simple operations.

Pizza fractions

Fractions can be tricky, so this activity can really help students to visualize key concepts. Create an instruction sheet with five different fractions on each (you can create several so different students get a different set). Students should create a pizza (using construction paper, or even the inside of an empty pizza box) and decorate the toppings to represent each fraction.

For example, if they had a quarter (fourth), they should cover one-quarter of the pizza with a specific ingredient (e.g. mushrooms or pepperoni).

'Lengthy' scavenger hunt

Divide students into groups and give each group a list of measurements and a measuring tool (e.g. a ruler, tape, trundle wheel). Instruct students to find items that are exactly the length of what they have listed. For younger students who haven't yet been introduced to measurement, draw various lines on their sheet and ask them to find items that are exactly the same length.

Make sure you prepare items beforehand and place them in a safe and visible spot. This activity can be done outside or in the classroom.

Survey and graph

Ask each student to think of a question they’d like to survey their fellow classmates on. For example, they might like to ask their classmates what their favorite animal is out of a dog, monkey, pig, or chicken. Give students time to walk around the classroom quizzing each other and recording their data.

Once students have collected enough data, ask them to represent their results by building a bar graph using linking cubes, blocks, or Legos. They can use sticky notes or bits of paper to create labels above each bar. Take a photo of each student's graph, which you can later print out to create a class collage to display.

Looking for new ways to make elementary math fun? Mathseeds is a research-based online math program specifically designed for students in grades K–2. Created by a highly experienced team of elementary teachers, Mathseeds provides self-paced lessons, fun games, automated reporting, and a range of teaching tools to help your elementary math students succeed. Sign up for a free trial today.

60 Elementary Hands-On Math Teaching Ideas

Counting Hands-On Learning Learning Games Math

  • Share
  • Tweet

This post may contain affiliate links.

Hands-on learning is incredibly important for kids. There are a million reasons why!  Today I am highlighting more than 60 elementary hands-on math teaching ideas that I have featured over the years on my site. This list will continues to grow, too! I love teaching math in creative ways!

Check out my post with The BEST Hands-on Math Supplies that we love.  Then browse through my list below highlighting all of the fun ways you can teach math to elementary-aged kids.

If You want even more ideas, be sure to check out my new book Math Art & Drawing Games for Kids!

 

Hands-On Math: Fractions & Decimals

There are loads of fun ways to teach fractions here on my site. There are just so many cool ways to teach them. We are only just getting into decimals around here, so watch for more on that, too!

1. Fraction Trees

2. Pi Puzzle

3. Snowman Fractions

4. Roll a Whole Fraction Game

5. Fraction Flowers

 

6. Hershey Fractions

7. Fractions With Flags

$ Skittles Math

8. Skittles Math

9. Fraction Decimal Percentage Puzzles

10. Fraction Cookies

11. Each Orange Had 8 Slices

12. Pizza Fractions

 

Hands-On Math: Shapes & Geometry

Geometry is a wonderful thing to start teaching at an early age. The younger kids understand these concepts, the easier upper level math will be for them.

13. 3-D Paper Shapes

14. Area & Perimeter City

Stellated Dodecahedron Template

15. Make a Stellated Dodecahedron

16. Volume of 3-D Shapes

17. Pentominoes

18. Licorice Shapes & Angles

19. STEM Construction Toys: Zome Tools

20. Marshmallow & Toothpick Geometry

 

21. Perler Bead Tangrams

22. Rainbow Icosahedron Ball

23. Heart Shaped Math Puzzle from Hand Made Kids Art

24. How to Make a Circle Geoboard

25. Gingerbread House Geometry

26. Geometric Shapes Activity from Little Bins for Little Hands

 

Hands-On Math: Counting, Addition & Subtraction

This is where math begins. Let your kids know  how much fun math really can be with these creative teaching ideas for addition, subtraction and counting.

27. Lock & Key Addition Puzzles

28. Pascal’s Triangle

29. Hundred Chart Puzzle

30. Hundred Chart Learning Ideas

31. Place Value Cards

32. Place Value Flip Chart

33. Teaching Greater Than & Less Than from Only Passionate Curiosity

34. Leap Frog Math

35. Math Checkers

 

 

36. Make Ten Math Game

37. Popsicle Stick Math

38. Roll the Digits Math Game

39. Eye Dropper Dot Counting

 

40. Build a House Math Bingo

$ Roll a Beetle Dice Game

41. Roll a Beetle Math Game

42. Kinetic Sand Math from Left Brain Craft Brain

43. Safe Cracker Math Game

44. Dice Games for Early Math: from Danya Banya

 

45. Math Grid Game

46. Building Lego Numbers from Little Bins for Little hands

47. Human Board Game from True Aim Education

 

Hands On Math: Multiplication & Division

Just when math starts getting a little harder is when kids start to tune out. Keep it interesting with creative multiplication and division teaching ideas.

48. Multiplication Grid Game

49. Target Number Card Game

50. Count the Dots Multiplication Game

 

51. Math Wheels

52. Division With Money Puzzles

53. Fun Ways to Teach Division to Kids

54. Mondrian Style Fibonacci Art

55. Math Fact Families

56. Multiplication Houses

57. Doubles Math Puzzles

$ Number Multiples: Multiplication Helpers

58. Skip Counting Multiplication Helpers

59. Spill The Beans Game

60. One Grain of Rice Math Lesson

 

Hands On Math: Money & Time

These essential math skills can seem dry for kids, but here are a couple of great ways to have fun teaching and learning them!

$ The Money Game

61. The Money Game

62. Chalkboard Clock

63. Play Store

64. Shadow Sun Dial

65.  Grouchy Ladybug Clock Stories

 

Hands-On Math: Weights & Measurements

Measure and weigh in unique ways! Check out these cool ideas.

66. Hershey Weights & Measurements

67. Weighing with Pennies

68. Math Paper Tricks

69. Gallon Man 

70. Measuring with Magna-Tiles from Go Science Girls

 

 

This is part of the iHN Hands-On Homeschooling link-up. Check out what the rest of the iHomeschool Network bloggers shared!

 

AWESOME Rainbow Experiments With Kids

Clover Word Families: St. Patrick's Day Learning Idea


2 Comments

Textbook for secondary school students ONLINE

Higher mathematics. Mathematics for non-mathematicians / Selected / Mathematics / Mathematics for students, graduate students and researchers N. V. Bogomolov. - 6th ed., Sr. - M .: Vyssh. school, 2003.— 495 p.
This manual (5th ed.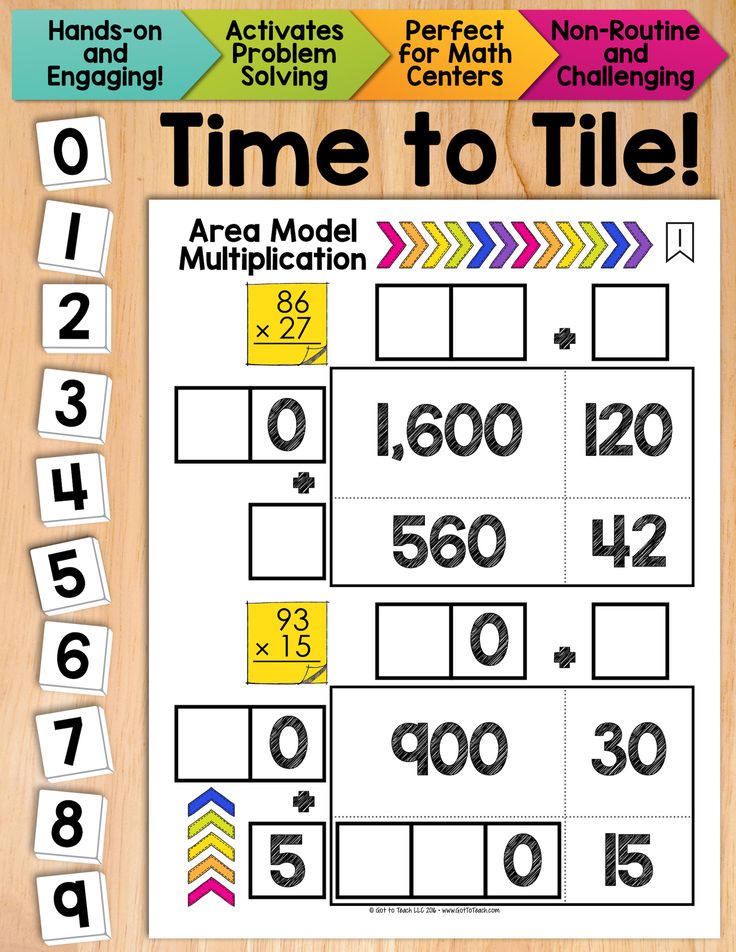 - 2002) is a guide to solving problems in all sections of the mathematics program for technical schools on the basis of incomplete and complete secondary schools.
The main purpose of the manual is to help the student independently, without the help of a teacher, learn the techniques for solving problems in mathematics, consolidate and deepen the skills acquired in solving these problems.
For students of secondary specialized educational institutions. Can be used by college students.
It is known that solving problems in mathematics for students is often associated with many difficulties. The main purpose of this manual is to help the student overcome these difficulties and teach him how to solve problems in all sections of the mathematics course.

When solving problems on their own, many students need constant consultations on techniques and methods for solving them, since they cannot find a way to solve a problem without the help of a teacher or an appropriate manual. The student can receive such advice in this book.

In each paragraph, brief theoretical information is given, methods for solving typical problems are described, their classification and solutions are given, and then tasks for independent solution follow, to which answers are given at the end of the book. After studying each topic, mixed problems on this topic are given, as well as a test work. This form of presentation allows the student to first get acquainted with the methods of solving typical problems and recording their solutions, and then begin to develop skills in their independent solution.
CONTENTS
Foreword .............................................. ....9
Section I. Elements of Computational Mathematics
Chapter 1. Errors in the Approximate Values ​​of Numbers ..................10
§ 1. Absolute Error in the Approximate Values ​​of a Number. Absolute error limit .......... 10
§ 2. Correct digits of a number. Recording the approximate value of a number. Rounding of approximate values ​​of numbers ..................................11
§ 3. Relative error of the approximate value of a number ..................................11
.13
Chapter 2. Operations with approximate values ​​of numbers .................14
§ 1. Addition of approximate values ​​of numbers .................. .................14
§2. Subtraction of approximate values ​​of numbers...............................15
§ 3. Multiplication of approximate values ​​of numbers....... ....................16
§ 4. Division of approximate values ​​of numbers .............................. .......17
§ 5. Raising to a power of approximate values ​​of numbers and extracting a root from them ..............18
§ 6. Calculations with predetermined accuracy...... .................18
§ 7. Solving right-angled triangles using a microcalculator .............. 19
§ 8. Solving oblique triangles ........................................ .............. 21
§ 9. Mixed problems .............................. ..................24
Section II. Algebra and the Beginnings of Analysis
§ 1. Solving linear equations with one variable ..................................25
§ 2. Solving linear inequalities with one variable... ...................28
§ 3. Systems and collections of inequalities with one variable .......... 29
§ 5. Solution of systems of two linear equations with two variables... 34
§ 6. Solution of systems of three linear equations with three variables... 37
§ 7. Solution of quadratic equations......... ................................................39
§ 8. Properties of the roots of a quadratic equation. Factorization of a square trinomial ..........41
§ 9. Solving equations reducible to quadratic equations ..................................................43 ..............................45
§ 11. Graphical solution of quadratic inequalities .......... .................... ..................46
§ 12. Irrational equations .......................... ......................48
§ 13. Irrational inequalities with one variable .............................. .........51
§ 14. Nonlinear systems of equations and inequalities with two variables ..........52
§ 15. Problems for the compilation of systems of equations .............................................. 55
§ 16. The simplest problems of linear programming with two variables .........55
Chapter 4. Function. Logarithmic and exponential functions............................58
§ 1. Function. Domain of definition and set of values ​​of a function ....58
§ 2. Logarithmic function .................................. ...............60
§ 3. Exponential equations .............................. ....................62
§ 4. Systems of exponential equations....................................64
§ 5. Exponential inequalities. .............. ...........................65
§ 6. Logarithmic equations. ..................................................66
§ 7. Systems of logarithmic equations.. ..................................................68
§ 8. Logarithmic inequalities ............................. ..............................68
§ 9. Mixed problems....................... ...................................................69
Chapter 5. Infinite number sequence. Sequence limit ....71
§ 1. Infinite number sequence...............................................71
§ 2. Limit of number sequence.... .........................73
Chapter 6. Function limit .................. ............................... 76
§ 1. Calculation of the limit of a function ............... ..............................76
§ 2. The number e. Natural logarithms .............. .................................81
§ 3. Mixed problems .................................. ........................ ......82
§ 4. Argument increment and function increment .......... ............83
§ 5. Continuity of function...............................................84
§ 6. Breakpoints of a function.......................................................86
§ 7. Asymptotes ............................................... .............87
§ 8. Solution of fractional-rational inequalities by the interval method ..............89
Chapter 7. Derivative .............. ..................................92
§ 1. Rate of change of function .......... .................92
§ 2. Derivative .................................. .........................94
§ 3. Basic rules of differentiation. Derivatives of the degree and root ......95
§ 4. Derivative of a complex function .................................. .....98
§ 5. Physical applications of the derivative .................................100
§ 6. Derivatives of logarithmic functions .......... .......................... 102
§ 7. Derivatives of exponential functions ..... .............................103
§ 8. Mixed problems ............................... ..................................104
Chapter 8. Applications of the derivative to the study of functions...... ..........105
§ 1. Increasing and decreasing function....................................................105
§ 2. Investigation of a function to an extremum using the first derivative ..107
§ 3. Investigation of a function to an extremum using the second derivative ..110
§ 4. The smallest and largest values ​​of a function............. ........... 111
§ 5. Problems of finding the smallest and largest values ​​of quantities ........ 111
§ 6. The direction of the convexity of the graph of a function .......... ........................... 113
§ 7. Inflection points ..................... .................................114
§ 8
Chapter 9. Trigonometric functions. ..............................................118
§ 1. Radian measurement of arcs and angles .............................................. 118
§ 2. Single numeric circle .........................................121
§ 3. Trigonometric functions of a numerical argument ...................... 123
§ 4. Signs, numerical values, and even and odd properties of trigonometric functions .............. .....124
§ 5. Basic trigonometric identities..................................................128
§ 6. Periodicity of trigonometric functions...... .........................................132
§ 7. Inverse trigonometric functions .................................. ......................134
§ 8. Construction of an arc (angle) by a given value of a trigonometric function ..............135
§ 9. Trigonometric equations............. .............................140
§ 10. Trigonometric inequalities ............................... ............... ..........145
§ 11. The property of the half-period of sine and cosine .............................. 147
§ 12. Reduction formulas.... ...........................................148
§ 13. Mixed problems ...................................................149
§ 14. Trigonometric functions of the algebraic sum of two arguments (addition formulas) .............. 150
§ 15. Mixed problems .............................. ..............................154
§ 16. Trigonometric functions of doubled argument .......... .............155
§ 17. Trigonometric functions of half argument .............................. 157
§ 18. Mixed problems .............. .............................................169
§ 19. Transformation of the product of trigonometric functions into an algebraic sum............162
§ 20. Transformation of the algebraic sum of trigonometric functions into a product .................163
§ 21. Transformations using an auxiliary argument. .... .........166
§ 22. Mixed problems .................................. .................................168
§ 23. Calculation of limits of trigonometric functions. The limit of the ratio .................169
§ 24. Derivatives of trigonometric functions ........................171
§ 25. Derivatives of inverse trigonometric functions .................................. 173
§ 26. The second derivative and its applications .. .................................................174
§ 27. Harmonic vibrations ...............................................175
§ 28. Basic properties of trigonometric functions....................................177
§ 29. Plotting trigonometric functions..................................................177
§ 30. Mixed problems.... ...............................................178
Chapter 10. Function differential. Application of the Differential to Approximate Calculations 180
§ 1. Calculation of the Differential of a Function . ................. § 2. Absolute and relative errors .............................. 181
§ 3. Calculation of the approximate numerical value of a function ...... ..........182
§ 4. Formulas for approximate calculations .............................................. 183
§ 5. Calculations according to the method strictly accounting for errors .................................. 184
§ 6. Mixed problems .................................. .................................187
Chapter 11. Indefinite integral .......... ..............................188
§ 1. Basic integration formulas. Direct integration ...188
§ 2. Geometric applications of the indefinite integral .................194
§ 3. Physical applications of the indefinite integral .......... .............196
§ 4. Integration by the change of variable method .............................. 198
§ 5. Integration by parts.... .................................................201
§ 6. Integration of some trigonometric functions. .................203
§ 7. Mixed problems .................................. ..................204
Chapter 12. Definite Integral .................. .........................205

§ 2. Calculation of the definite integral by the change of variable method .......... 208
§ 3. Integration by parts in a definite integral ......... 210
§ 4. Approximate Calculation of Definite Integrals .................................. ..............212
§ 1. Application of the definite integral to the calculation of various quantities. The area of ​​a flat figure ........ 212
§ 2. Calculation of the path traveled by a point .................................. .219
§ 3. Calculation of the work of a force .................................................... ..221
§ 4. Calculation of the work performed when lifting a load .................223
§ 5. Calculation of the pressure force of a liquid .......... .. .....................225
§ 6. Arc length of a plane curve ........................ .......................227
Chapter 14. Complex numbers .......................... .................................. 229
§ 1. Complex numbers and their geometric interpretation .............................. ..229
§ 2. Actions on complex numbers given in algebraic form ..........233
§ 3. Actions on complex numbers given in trigonometric form......235
§ 4. An exponential function with a complex exponent. Euler's formulas...............239
§ 5. Mixed problems............................................. ...............242
Chapter 15. Differential Equations .................................. ......243
§ 1. Differential equations of the first order with separable variables ..........243
§ 2. Problems for the formulation of differential equations.......... ...................245
§ 3. Linear differential equations of the first order ............. .......248
§ 4. Incomplete differential equations of the second order ................................... .250
§ 5. Linear homogeneous differential equations of the second order with constant coefficients ..................253
§ 6. Mixed problems .......... ....256
Chapter 16. Elements of combinatorics and probability theory ..........................257
§ 1. Elements of combinatorics..... .............................................257
§ 2. Random events. Probability of an event .................................... 260
§ 3. Theorems of addition of probabilities ....... .............................. 262
§ 4. Probability multiplication theorems .............. ......................264
§ 5. Total probability formula. Bayes formula .................................. 265
§ 6. Repetition of tests. Bernoulli's formula...............................266
§ 7. Mixed problems.......... ............................................. ...267
Section III Geometry
Chapter 17. Vectors on the plane................................................. ....268
§ 1. Basic concepts and definitions .................................. .269
§ 2. Addition and subtraction of vectors. Multiplication of a vector by a number .... 270
§ 3. Rectangular coordinate system .................................. .273
§ 4. Vector length. The distance between two points on a plane. Angles formed by a vector with axes of coordinates .......... 276
§ 5. Division of a segment in this respect .................. ..............278
§ 6. The scalar product of two vectors...............................279
§ 7. Rectangular coordinate transformations... ........................... 281
§ 8. Polar coordinates ..................... ............................... 283
§ 9. Mixed problems ............................... .......................284
Chapter 18. A straight line in a plane and its equations . ................. .....286
§ 1. General equation of a straight line. Vector and canonical equations of a straight line .......... 286
§ 2. Equation of a straight line in segments on axes .......................... ............289
§ 3. Equation of a straight line with a slope .................................................290
§ 4. Equation of a straight line, passing through a given point in a given direction .......... 293
§ 5. The equation of a straight line passing through two given points .............. 294
§ 6. Intersection two straight lines..............................................295
§ 7. Angle between two lines .............................. 296
§ 8. The condition of parallelism of two lines .... .................................299
§ 9. The condition of perpendicularity of two lines .................................................300
§ 10. Mixed problems. ................................................. ....302
Chapter 19. Curves of the second order .............................................. ......304
§ 1. Sets of points on the plane.................................................. .....304
§ 2. Circle .................................. ......................306
§ 3. Ellipse...................... .........................................310
§ 4. Hyperbole .............................................. ...............312
§ 5. Parabola with vertex at the origin .............................. ....... 315
§ 6. Parabola with displaced vertex .................................. .....318
§ 7. Tangent and normal to a curve .................................. ....321
§ 8. Mixed problems .............................................. ..............326
Chapter 20. Lines and planes in space .............................. ......327
§ 1. Parallelism of lines and planes .................................327
§ 2. Perpendicularity in space. Dihedral and polyhedral angles . ......... 330
§ 3. Mixed problems .............................................. .........................333
Chapter 21. Vectors in space .................. .........................335
§ 1. Basic concepts. Rectangular coordinate system in space .......... 335
§ 2. Scalar product of vectors in space .............................. .339
§ 3. Vector product .............................................. ...340
§ 4. Mixed problems .............................................. ..............342
Chapter 22. Equations of a straight line and a plane in space ........................343
§ 1. Plane................................................. ..........343
§ 2. Straight line in space.................................. ...............347
§ 3. Plane and straight line .............................. 350
§ 4. Mixed problems .................................. .........................352
Chapter 23. Polyhedra and their surface areas. ................................353
§ 1. Prism........ ................................................. ..353
§ 2. Surface area of ​​a prism.................................................. ..355
§ 3. Pyramid. Truncated Pyramid.......................................357
§ 4. The surface area of ​​the pyramid and the truncated pyramids .................. 360
§ 5. Mixed problems .............................. 361
Chapter 24. Shapes of rotation .................. ..............................363
§ 1. Cylinder ............................................... .............363
§ 2. Cone. Truncated cone ..............................
§ 3. Sphere. Ball................................................. .....365
§ 4. Inscribed and circumscribed spheres.................................................. ...
§ 5. Mixed tasks .......................................... ...... 369
Chapter 25. Volumes of polyhedra and figures of revolution . ..................... 370
§ 1. Volume of a parallelepiped and a prism... ................................370
§ 2. The volume of the pyramid .............................................. .....372
§ 3. The volume of a truncated pyramid .............................. ..373
§ 4. Investigations on an extremum in problems on the volumes of polyhedra ..........373
§ 5. The volume of figures of revolution .................. .........................................374
§ 7. Calculation of the volumes of figures of revolution with the help of a definite integral 378
§ 8. Mixed problems ...................................................... .......................381
Chapter 26. Areas of surfaces of figures of revolution....................................383
§ 1. Areas of lateral and full surfaces of a cylinder. ....................383
§ 2. Areas of the lateral and full surfaces of the cone .......................... ...384
§ 3. Areas of the lateral and complete surfaces of a truncated cone . .........385
§ 5. Investigations for extremum in problems on the area of ​​surfaces of figures of revolution .........386
§ 6 Calculating the areas of surfaces of figures of revolution using a definite integral .............................................387
§ 7. Mixed problems .............................................. ....389
Section IV Supplementary Chapters
Chapter 27 Rows .................................. ....................... 391
§ 1. Numerical series .......... ....................................391
§ 2. Necessary criterion for the convergence of a series. Sufficient criteria for the convergence of series with positive terms 395
§ 3. Sign-alternating and alternating series. Absolute and conditional convergence. The Leibniz Convergence Test for Sign-Alternating Series .........................400
§ 4. Calculation of the sum of the terms of an alternating series with a given accuracy and estimation of the remainder of the series . ................................403
§ 5. Power series ........ ...............................................405
§ 6 Expansion of functions in power series...............................................409
§ 7 Application of Power Series to Approximate Calculations of the Values ​​of Functions 416
§ 8. Calculation of Definite Integrals with the Help of Power Series 417
Chapter 28. Fourier Series. ................................................. ........419
§ 1. Trigonometric Fourier series .................................................. ...419
§ 2. Fourier series for an odd function .............................................. ..423
§ 3. Fourier series for an even function .............................................. ....... 426
§ 4. Fourier series expansion of a function given in the interval .............. 428
§ 5. Fourier series expansion of a function, given in an arbitrary interval .......... 430
§ 6. Expansion in Fourier series of some functions that are often encountered in electrical engineering . .... 433
Chapter 29 .......435
§ 1. Functions of several variables.................................................. 435
§ 2. Partial derivatives and the total differential .............................................. 438
§ 3. The Double Integral and Its Calculation.......................439
§ 4. The Double Integral in Polar Coordinates...... .........................447
§ 5. Calculation of the area of ​​a plane figure .................. ....................450
§ 6. Calculation of the volume of a body .............................................. 451
§ 7. Calculation of the surface area .................................. ..........454
§ 8. Calculation of the mass of a flat figure .............................. 459
§ 9. Calculation of the static moments of a plane figure .............................. 460
§ 10. Coordinates of the center of gravity of a plane figure .................................................. 463
§ 11. Calculation of the moments of inertia of a plane figures............................466
Answers .................................................. ..466

GDZ to the collection is here: http://math-helper.ru/reshebniki-po-matematike/reshebnik-k-sborniku-zadach-po-matematike-dlya-tehnikumov-bogomolova-n-v-onlayn Read online Math Practice » Retrokniga



Bogomolov, N.V. Practice Math » Retrokniga We are right! More details

Main - Natural and technical sciences - Mathematics, logic - Bogomolov, N.V. Practice Mathematics

Filters

  • Fiction
    • Detectives, horror
    • Historical novel
    • Classic
    • Love story
    • Memoirs, documentaries
    • About the war
    • Poetry
    • Adventure, travel
    • Satire, humor
    • Soviet literature
    • Contemporary Literature
    • Fantasy
    • Folklore
  • Natural and technical sciences
    • Architecture, construction
    • Astronomy, astronautics
    • Biology, animals
    • Geography, geology
    • Computers, programming
    • Mathematics, logic
    • Medicine, sports, health
    • Metallurgy
    • Industry, manufacturing
    • Engineering, electronics
    • Transport
    • Physics
    • Chemistry
    • Drafting
  • Social and Human Sciences
    • Astrology, unknown
    • Military
    • Business literature
    • History
    • Science, invention
    • Pedagogy
    • Politics, sociology
    • Psychology, relationships
    • Religion, occultism
    • Philosophy
    • Ethics, aesthetics
    • Ethnography
    • Legal literature
    • Language, literature
  • Children's literature
    • Cognitive
    • Artistic
  • culture
    • Fine arts
    • Music, singing
    • Theatre, cinema
    • Theory and History of Art
  • Hobbies
    • Collecting, book business
    • Cooking, home economics
    • Fashion, beauty
    • Board games, entertainment
    • Beekeeping
    • Repair, DIY
    • Needlework, sewing
    • Fishing, hunting
    • Garden, vegetable garden
    • Photography, photography

Second hand book

not available

Publisher: M.

Learn more