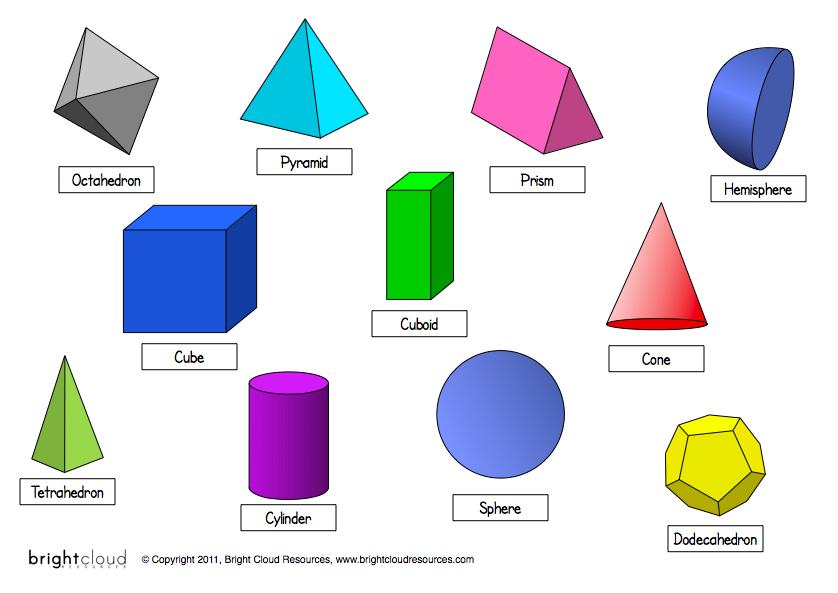
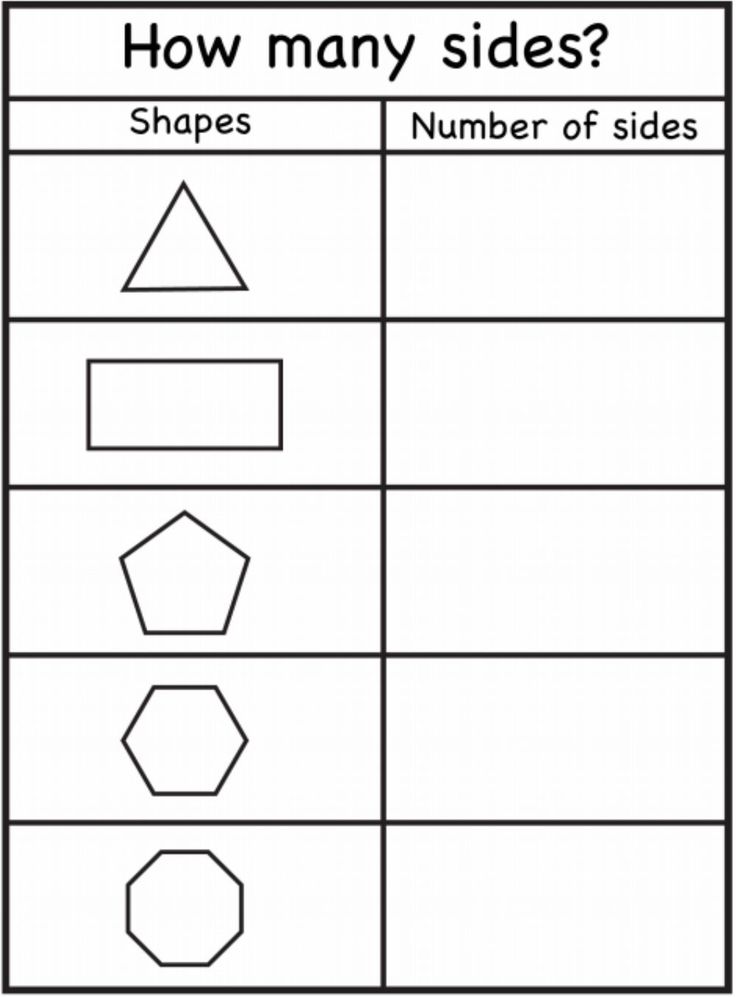
How many basic shapes are there
What are the 16 Basic Shapes?
24 Feb What are the 16 Basic Shapes?
We may not realize this, but shapes are all around us. We come across items of every shape in our home, out on the streets and in nature. Shapes can be a rectangular prism building, a sphere shape football, the crescent moon during a certain time of the month and even the oval-shaped of our eyes.
Children are first introduced to shapes as young children at a preschool level. In primary school, they learn about geometric shapes such as the circle, square, triangle and etcetera. At the most basic level, they are first taught how to identify and name the shapes, they will then be exposed to calculating the perimeter and area (2D shapes) and volume (3D shapes) using the specific formula for each shape.
After mastering the above calculations children will then be taught to apply them in problem-solving questions involving composite shapes (more than one shape) and real-world scenarios.
When it comes to questions involving real-world scenarios your child may find it difficult at first to apply the basic calculations that they have learned into more complex questions that require some imagination on their side.
We have compiled a list of the 16 basic shapes for your child to get to know and where they may be able to spot them.
The Circle
The circle is very easily identified in the world around your child. It could be the clock on the wall, a classmate’s harry potter style glasses, a merry go round in the park, a roundabout on the road and a full moon which appears once a month.
A semicircle is a circle that has been separated into half.
Formula:
Radius of circle = r
Circle
Circumference = 2πr Area = πr2
Semicircle
Perimeter= ½ (2πr) + 2r
Area= ½πr2
The Oval/Ellipse
Although not as commonly spotted as the circle, your child will be able to spot the oval shape in wall and handheld mirrors, in fruits such as the watermelon and the kiwi and even the oval-shaped of eggs.
Another classic example of an oval-shaped object would be the ball used in American football.
The Square
Children will certainly be familiar with the cartoon character ‘Spongebob Squarepants’ and his pair of iconic pants. The square shape is easily identifiable as one of the most common shapes for everyday items such as tables, photo frames and most biscuits that your child will snack on.
Formula
Length of sides = l
Perimeter = l + l + l + l = 4l
Area = l × l
The Rectangle
Take your child on a grocery shopping trip and they are bound to see rectangular packaging of all sizes for food and other household items on the display shelves. Your child’s textbooks and exercise books are almost always rectangular in shape. Another rectangle shape item that your child may be familiar with would be the screens on the smartphone and computers.
Formula:
Length of sides = x (width) and y (length)
Perimeter= 2x + 2y
Area= x × y
The Triangle
Your kids may be familiar with a triangular instrument often seen in movie scenes depicted an orchestra or music lesson, the triangle which is a kind of percussion is an interesting piece of instrument used by classical musicians.
Other examples of triangles in our daily lives sails on a boat which helps to stir the boarding against and along the direction of the wind.
Formula:
Height of triangle = h
Base of triangle = B
Length of sides = l
Perimeter= sum of length of sides
Area= ½ × h × B
The Rhombus/Diamond
The Rhombus or same may also call it the diamond is a shape with four sides that has opposite angles that are equal, unlike the square which has four right angles. The rhombus shape can often be seen in kites and also the diamond shape in playing cards.
Formula:
Diameter of rhombus=d1 and d2
Perimeter= sum of length of sides
Area= = ½ × d1 × d2
The Trapezium
The trapezium has four side. Its top and bottom bases are parallel while its sides are usually not parallel. Some examples of trapezium objects are the popcorn boxes used by the cinema and ladies’ handbags which are usually trapezoid in shape.
Formula:
Length of sides = l1 + l2
height of trapezium = h
Perimeter = sum of length of sides
Area = ½ × ( l1 +l2 ) × h
The Pentagon (Polygon with 5 sides)
A pentagon is a polygon that has five sides. The pentagon can be symmetrical (the length of its sides and interior angles are the same) or asymmetrical (different side lengths and interior angles).
One very famous landmark in the USA is shaped and named after the pentagon, located in Arlington County in the state of Virginia, The Pentagon is the headquarters of the US Department of Defence. A birdhouse where birds cans seek shelter can also be built in the shape of a pentagon.
Formula:
Perimeter= sum of length of sides
Area= ½ x perimeter x apothem (length of midpoint of side to centre of circle)
Exterior angle of a regular pentagon = 360° / 5 = 72 o
Sum of Interior angle of a regular pentagon = (5-2) x 180 o = 540 o interior angle = 540° / 5 = 108 o
The Hexagon (Polygon with 6 sides)
Of similar character as the pentagon, the hexagon can be spotted in nature inside a honeycomb.
Honey bees construct hexagonal honeycombs as this is the most effective way for them to store their honey. Pencils and colour pencils also have a hexagonal shape, this ensures that the pencils can be efficiently stacked up for storage and will not easily fall off the table.
Formula:
Perimeter = sum of length of sides
Area= ½ x perimeter x apothem (length of midpoint of side to centre of circle)
Exterior angle of a regular pentagon = 360 o / 6 = 60 o
Sum of Interior angle of a regular hexagon = (6-2) x 180 o = 720 o , interior angle = 720° / 6 = 120 o
The Octagon (Polygon with 8 sides)
The octagon is an eight-sided polygon that is less commonly used and seen compared to the hexagon and pentagon. The octagon is normally used in the design of windows and tiles for aesthetic effect. However, one octagonal-shaped object that we may see around is the stop sign on the road.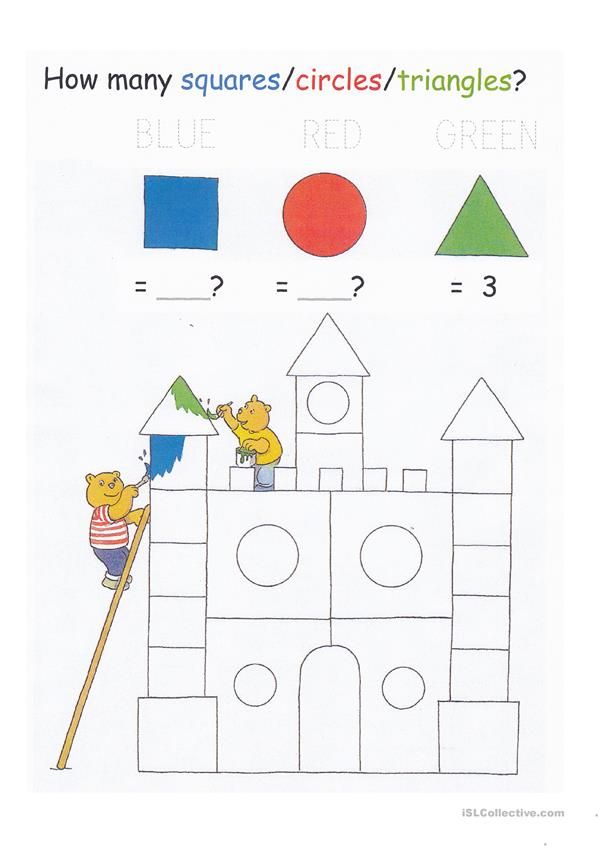
Formula:
Perimeter= sum of length of sides
Area= ½ x perimeter x apothem (length of midpoint of side to centre of circle)
Exterior angle of a regular pentagon = 360 o / 8 = 45 o
Sum of Interior angle of a regular octagon = (8-2) x 180 o = 1080 o , interior angle = 1080 ° / 8 = 135 o
The Cylinder
A cylinder is a 3D solid or hollow object with a curved surface and circles at the side of both ends
Some examples of solid cylinders we see in our daily lives are batteries and canned food and soft drinks. Hollow cylinders are those that are hollow on their insides such as the pots and pans used for cooking and also buckets.
Formula:
Radius of circle = r
Height of cylinder = h
Base of cylinder (circle) = B = πr2
Solid cylinder
Total surface area = 2πrh × 2 πr2 Volume= B × h
Hollow cylinder
Total surface area = lateral surface area (external + internal) + areas of solid bases
= (2πr1 h + 2πr2 h ) + 2π (r12-r22 )
Volume= Volume of external cylinder – Volume of internal cylinder
Volume = B1 × h – B2 × h
The Cone
A cone is a geometrical solid with a round base and only one vertex.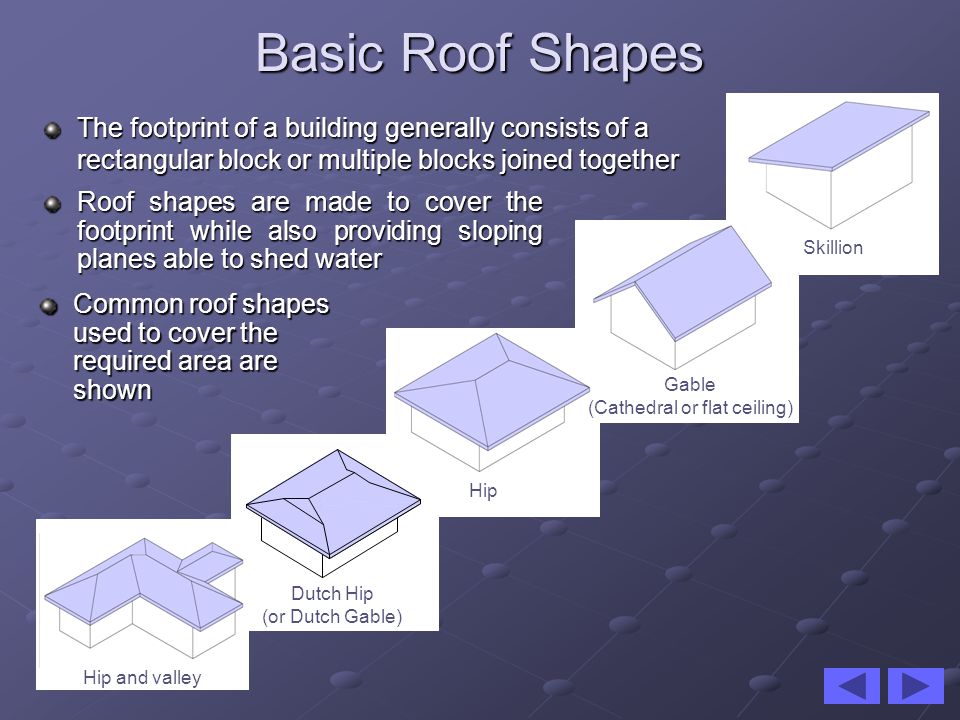
Some commonly seen conical objects are the orange traffic cone and also the ever-popular ice cream cone.
Formula:
Radius of circle = r
Height of cone = h
Slant height = s
Total surface area= lateral surface area + area of circle base
TSA = πrs + πr2
Volume = 1/3 πr2h
The Cube
The cube is essentially a solid made out of six square surfaces. Some examples of the cube are the Rubik’s cube consists of 27 smaller cubes inside one big cube. Dices used during board games are also cubes.
Formula:
Total surface area = 6 × area of square
Volume = width × length × height = w + l + h
The Cuboid/Rectangular Prism
Similar to the cube a cuboid is a solid made out of six rectangular faces. Some cuboid objects that your child may come across are Legos in a Lego set, shoe boxes when purchasing new shows or even the microwave at home.
Formula:
Total surface area = Sum of area of each rectangle
Volume = width × length × height = w + l + h
The Pyramid
The Great Pyramid of Giza was a great feat of architecture built by the ancient Egyptians.
The Egyptian builders constructed the pyramid one block at a time with no room for error. The pyramid is a square-based pyramid. There are also pyramids that have triangular and rectangular bases.
Formula:
Total surface area = Area of 4 triangle surface + area of base (square/rectangle)
OR Sum of area of 4 triangle surface (for triangular based pyramid)
Volume = 1/3 × area of base (square/rectangle/triangle) × h, height
The Sphere
Our earth is a sphere as can be seen from outer space and also through a model of a globe. The calculation of points of location on the earth using longitude and latitude is based on the degree of a circle. The other planets are also spherical in shape.
Other sphere shape items are balls of all sizes and functions such as the soccer ball, volleyball, basketball and golf ball.
A hemisphere is a sphere that has been cut into half.
Formula:
Sphere Total surface area = 4πr2
Volume = 4/3 πr3
Hemisphere Total surface area = 3πr2
Volume = 2/3 πr3
Trust MLGS to Help Your Child with Mathematics
Maths Learning Groups was established by Mr.
Lawrence Ong, who is NIE-Trained and an ex Primary School Teacher with more than 15 years of teaching experience. We aim to help weaker students to bridge the gap with better-performing students by catering to their learning pace and style.
We strive to provide affordable tuition rates so that no student will be deprived of the opportunity to learn from NIE-Trained teachers. We specialize in offering primary school maths tuition classes for students in Primary 3 to Primary 6. Our primary maths tuition Singapore classes help to build up a strong solid foundation in the key mathematical concepts and help students visualize it in real-world scenarios.
Shapes – Definition with Examples
What are Shapes?
In geometry, a shape can be defined as the form of an object or its outline, outer boundary or outer surface.
Everything we see in the world around us has a shape. We can find different basic shapes such as the two-dimensional square, rectangle, and oval or the three-dimensional rectangular prism, cylinder, and sphere in the objects we see around us.
These geometric shapes appear in objects we see as credit cards, bills and coins, finger rings, photo frames, dart boards, huts, windows, magician’s wands, tall buildings, flower pots, toy trains, and balloons.
Different Types of Shapes
Shapes can be classified into open and closed shapes.
| In geometry, an open shape can be defined as a shape or figure whose line segments and/or curves do not meet. They do not start and end at the same point. | In geometry, a closed shape can be defined as an enclosed shape or figure whose line segments and/or curves are connected or meet. They start and end at the same point. |
Closed geometric shapes can further be put into two broad categories, namely two-dimensional and three-dimensional shapes.
| The 2-Dimensional shape is flat. | A 3-Dimensional Shape is a solid shape. |
| It has two dimensions, that is, length and width. | It has two dimensions, that is, length, width, and depth. |
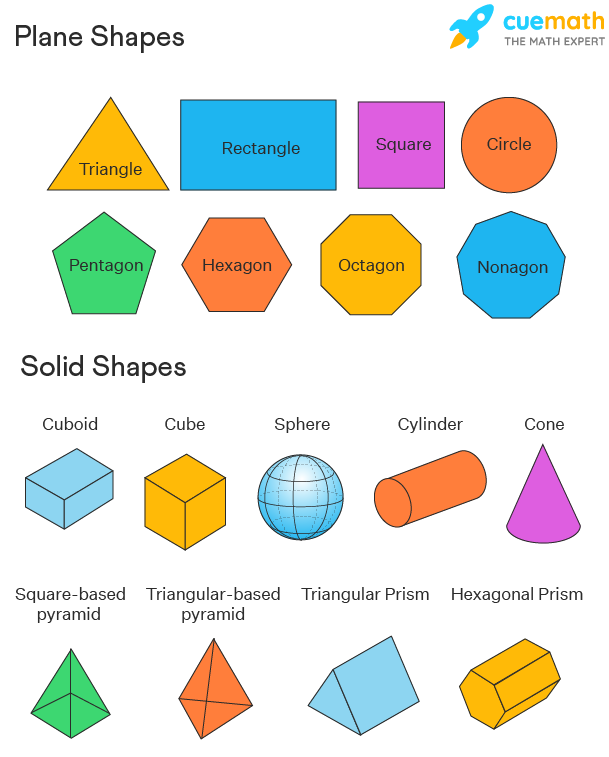
Here’s a list of 2-D or two-dimensional shapes with their names and pictures:
| Two-Dimensional Geometric Shapes |
Here’s a list of 3-D or three-dimensional shapes with their names and pictures:
| Three-Dimensional Geometric Shapes |
The color, overall size, and orientation called the non-defining attributes of a two-dimensional or three-dimensional shape do not define or affect the shape in any way. These attributes can change without any effect on the shape.
On the other hand, defining attributes such as the number of sides (parallel or non-parallel, straight or curved), vertices, edges, and faces of a shape, whether the shape is open or closed, and the angle measures determine the shape of a two-dimensional or three-dimensional object. Any change in these defining attributes will change the shape.
Solved Examples on Shapes
Example 1: Name the shapes.
- A polygon with 6 sides.
- Outline of a door.
- When you fold square corner to corner.
- A square and a triangle on top of it.
Solution:
- Hexagon
- Rectangle or quadrilateral
- Triangle
- Pentagon
Example 2: Classify the given letters as open shape or closed shape.
C, D, L, M, O, S, U, V, Z
Solution:
Open shape: C, L, M, S, U, V, Z
Closed shape: D, O
Example 3: Identify the solid shape of given objects.
- Globe
- Book
- Cold drink can
- Dice
Solution:
- Sphere
- Cuboid
- Cylinder
- Cube
Example 4: Why is the crescent-shaped moon not a polygon?
Solution:
Crescent shape moon is not a polygon as it has curved lines.
Practice Problems
hexagon
heptagon
octagon
quadrilateral
Correct answer is: octagon
A polygon with 8 sides is known as octagon.
1
2
3
depends on the shape
Correct answer is: 3
All solid shapes are 3-dimensional shapes.
closed shapes can have only straight sides.
closed shapes have definite area.
start and end point of a closed shape are the same.
start and end point of a open shape are the different.
Correct answer is: closed shapes can have only straight sides.
Closed shapes are shapes whose start and end points are the same. It is not necessary that it is formed by only straight sides.
we learn flat and three-dimensional geometric shapes
Masaru Ibuka in his book “After three it's too late” claims that in the first three years of life a child has the highest potential for learning and development, so inaction is akin to a crime.
Of course, we may feel that the child is too small.
And what can he learn if he cannot even speak? But the brain of a child, like a sponge, absorbs all the information around it. And it depends on the parents what the child will learn at this age.
Is it worth it to start learning geometric shapes at such an early age? Undoubtedly. The child lives in an environment of geometric shapes. The knowledge you give should not be divorced from your daily life. Mom is the guide of the baby in this world, and it is absolutely not necessary for her to have a degree in order to tell the child how the world works.
Why should a child learn geometric shapes?
The first three years of a child's life is a period of development of brain cells, when a solid foundation for new achievements is formed. Already at 3-4 months, the baby is able to distinguish forms. This does not mean that the time has come to memorize the names of geometric shapes, but when talking with a baby, a mother may try to use the phrases: “Here is our favorite round saucer”, “Let's see what's in a square box” and the like.
Knowledge of geometric shapes helps:
- develop spatial thinking, orientation in space;
- broaden one's horizons;
- develop the ability to compare, analyze, summarize and highlight the main thing, classify;
- to replenish vocabulary.
And, of course, the knowledge acquired by a preschooler will serve him as an excellent help in studying mathematics at school.
How to teach geometric shapes with a preschooler?
- Education for preschoolers should be built in the form of an exciting game.
- No need to scold the child if he did not remember the names of the figures from 1 time, even if from 31 - it's not worth it.
- Do not forget to organically weave geometric knowledge into life: “give a square box”, “take an apple from a round plate”.
- On the way to the garden, look for rectangular or round objects, compete to find and name the most.
- In the game arsenal you should have toys of the correct geometric shape - balls, cubes, designer parts.
- Usually kids like to help their mother in the kitchen. Get round, square, rectangular molds and bake edible geometric shapes.
- It is important to use tactile memory when studying figures. It will be much more interesting for a child not only to see, but also to feel, stroke, and maybe even lick the object of study.
- Load the child's brain in doses, gradually supplementing with information. For example, when studying shapes, repeat colors as well: “Look, what a blue oval it turned out to be.”
Basic Shape Memorization Techniques
There are many techniques and techniques that will make memorizing shapes interesting for children. The choice of methods will depend on the age and knowledge of the child.
- Before reaching the age of 1.5, we pronounce the surrounding objects aloud, supplying our story with information about the shape (let's take a round apple).
- At the age of 1.5 - 2 years, we use pictures, color the figures, use sorters to study the figures.
We start with the simplest - the circle. We will connect the rest of the figures only after the child has learned the concept of "circle". - From the age of 2 until reaching school age, we can apply all existing methods, following from simple to complex.
When studying geometric figures, it is important to proceed in stages. You should start with light shapes: circle, square, triangle, rhombus, rectangle, oval. Knowledge of these figures is available for children 2-3 years old.
Older children, 4-5 years old, include in their vocabulary and use the idea of a trapezoid, parallelogram, pentagon, hexagon, octagon, decagon and other polygons. They already know how to analyze, so they can easily compare and find differences between figures.
Senior preschool children get acquainted with three-dimensional figures: cylinder, pyramid, cube, ball, cone, prism.
Let's analyze some variants of techniques for studying geometric shapes:
1.
Sorter - looking for a "house" for each shape. The child will not only remember the figures, but will also develop fine motor skills, coupled with thinking.
2. Modeling . Sculpt geometric shapes with your baby - you simply can’t imagine a better activity for developing fine motor skills of hands and perseverance.
3. Three-dimensional stickers and magnets depicting geometric shapes can also help the child fix the names of the shapes in memory.
4. Looking for halves of . Cut the geometric shapes into two parts, mix and invite the baby to find the other half.
5. Applications . You can also make a geometric application from cut out figures. For example, a house (square + triangle), Christmas tree, car.
6. Outline dashed geometric shapes .
7. Color or shade the geometric shapes you suggested .
7. Finish the figure according to the sample.
8. Draw figures using stencils.
9. Listen to a fairy tale where the main characters are geometric figures, and then draw what you hear.
10. Put figures of different shapes into an opaque bag and suggest guessing the shape of the object by touch.
11. An excellent game for the development of memory and attentiveness. An adult prepares cut out figures of different colors and sizes and lays them out in front of the baby. They discuss colors, name the figures, and then the adult hides the figure. The task of the child is to find and name which figure is not.
12. Laying out geometric figures with counting sticks or matches. When the child masters this skill, you can move on to a more difficult level - solve puzzles. For example, remove one match to make a triangle.
13. Associations . Invite the child to name objects that a circle or rectangle looks like.
14.
Laces and various insert frames , for example, Nikitin squares, where you need to recreate a square from several objects, or Segen boards, where you need to insert the missing part.
15. Outdoor games . For example, an oval, a triangle, a square, a rectangle are drawn on the asphalt. At the command of an adult, the child must find the named figure and stand in it.
16. Videos . There are a large number of cartoons and educational materials about geometric shapes. Watch the video with the baby and be sure to discuss what you see.
17. Find on the Internet and print out pictures that artists draw with geometric shapes, and invite your child to count how many circles, rectangles, etc. are there. objects (for example, ball = ball). And, of course, to involve the study of the subject through games:
- Finding a three-dimensional figure from a flat pattern is an excellent exercise for developing spatial thinking.
- "Sleuth". Children are given an “orientation” - a flat drawing of the desired figure from all sides. Children need to match the pictures and find the right shape.
- Create a 3D model yourself. An adult can print stencils from the Internet. It remains for the child to bend along the lines and glue to make a figure.
- Models, origami - you can try with your child to create your own voluminous paper toy.
- Constructor. Build a tower or a castle for the princess with the help of details. This game will contribute to the development of fine motor skills, imagination, understanding the properties of three-dimensional figures.
The study of geometric figures should not become torture for a child and an adult. Choose the method that's right for you. Show patience and ingenuity, and then the result will not be long in coming. Most importantly, do not forget to encourage the child for his new discoveries and repeat the knowledge gained from time to time.
Mathematics and logic for children 7-13 years old
We develop logical thinking through solving plot mathematical problems in an interactive game format
learn more
Basic geometric shapes
geometric shapes exist around us. We meet them everywhere, in all the objects around us. Where are geometric shapes found in our lives?
Where are geometric shapes found in our lives?
Each of us, both adults and children, noticed how many geometric shapes exist around us. We meet them everywhere, in all the objects around us.
People have long been interested in the variety of geometric shapes. Even for primitive people, the shape of the objects surrounding them played an important role. Mastering the world, people got acquainted with the simplest geometric shapes. At first they made tools of relatively regular shape, then they learned how to improve them. At that time, of course, there were no special names for geometric shapes.
They were invented much later. When people began to build houses, they had to understand even more deeply the features of different figures in order to understand what shape walls and roofs should be given, what shape logs or stone blocks should be. Without knowing it, a person was constantly studying figures: women, making clothes, hunters - spearheads or boomerangs of complex shape, fishermen, making such bone hooks so that the fish would not fall off them.
One cannot live without this knowledge in the modern world.
Where are geometric shapes found in our lives?
Perhaps someone thinks that the various lines of the figure are "found" only in the books of learned mathematicians. However, if you look around, it becomes clear that many objects have a shape similar to the main geometric shapes. We just don't always notice it. Many wonderful geometric shapes are found in the nature around us. The field has the shape of a rectangle, the river has a curved line, the lake has a circle, a salt crystal has the shape of a cube, an ordinary pea, a dew drop has the shape of a ball.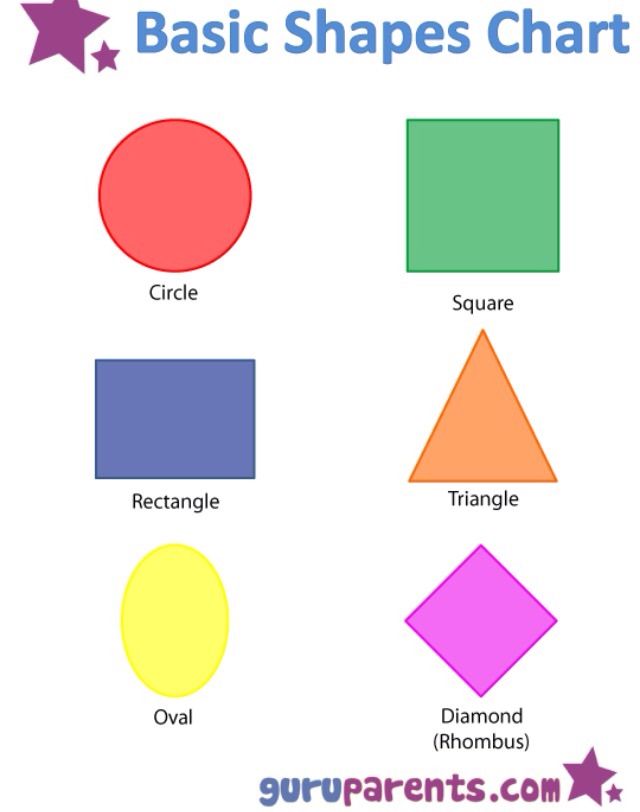
Beautiful and varied polyhedrons - crystals of rock crystal. But in everyday life, the basic geometric shapes are also everywhere. These are buildings, structures, transport, apartment interiors, even dishes and clothing. For example, a woman's skirt is a trapeze, a plate is a circle, a house is a square and a triangle, and a cylinder is in a pipe.
Knowing all the figures, their types, names and properties is very important. Systematizes knowledge about geometric shapes and studies their properties of mathematical science - geometry. This science is very important, its application is simply priceless at all times and regardless of profession. Neither a worker, nor an engineer, nor an architect, nor an artist can do without knowledge of geometry. And it is very important to start mastering this science at an early age.
An educational platform with iSmart smart exercise machines will be a great help to your child. The main types of geometric shapes, their properties, tasks for finding the area of figures and much more are on the platform in the "Mathematics" section https://www.
ismart.org/zanyatiya/matematika. Here are collected several thousand tasks for the development of these topics, which are not repeated during repeated development. Studying on the iSmart.org interactive online simulator, primary school students will thoroughly understand the basics of geometry, this will give them a good base in the subject for studying in middle and high school. In addition, interactive tasks are colorful, interesting, and exciting.
So,
The simplest types of shapes
The two basic shapes are a point and a line. The accumulation of points and lines forms various geometric shapes. Each of them is individual, differs in its parameters, their forms are very diverse. Figures are simple and complex, flat and voluminous.
Point
Point is the smallest, but at the same time the most important object in geometry. This is the smallest geometric figure, but it is it that is necessary for constructing other figures on the plane and is the basis for all other figures.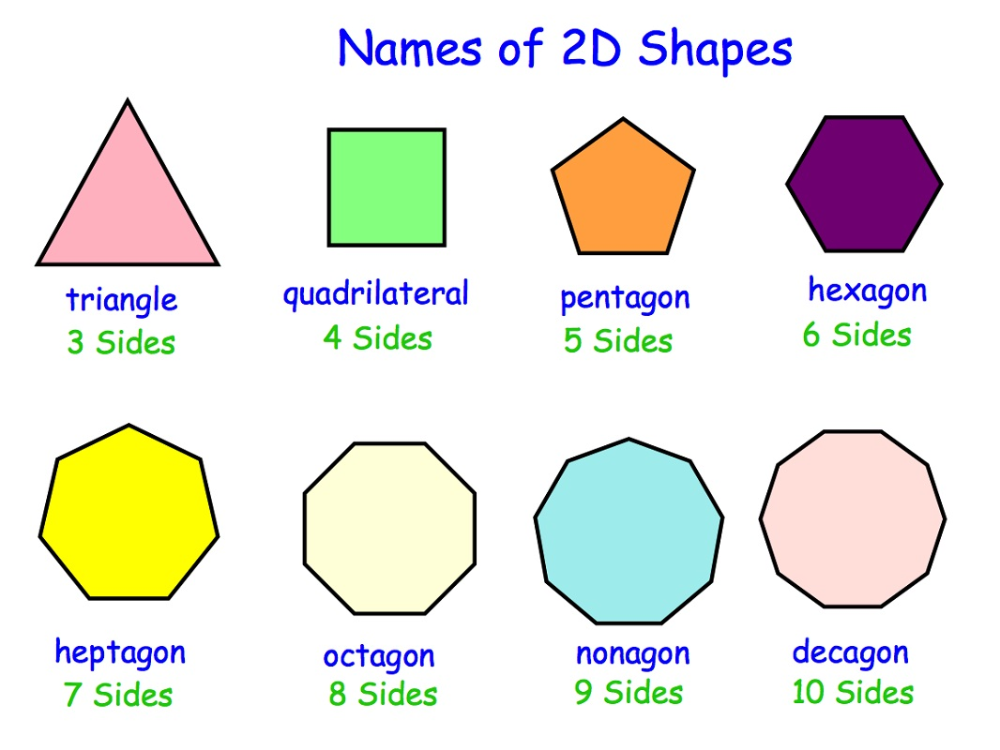
It does not contain such properties as length, height, volume, area, does not have measuring features and characteristics. It only matters where it is located. The point is indicated by a capital letter of the Latin alphabet or a number. For example, A, B, C or 1, 2, 3.
Any more complex geometric figure is a set of points , which have a certain property that is characteristic only for this figure.
The simplest figures are a ray and a segment.
- Ray is a part of a straight line that has a starting point but no end. This is a one way extension.
- Segment is a component of a straight line, which is limited by two points. It has a beginning and an end, so it is measured. The length of a line can be determined by measuring the distance between its ends.
Line
A line is formed from a set of dots arranged one after another and connected to each other. Lines are closed and open, straight and curved, as well as broken.
- Closed - when the start and end parts of the direction are located at the same point. An inverse version is obtained from an open line.
- Open - when the beginning and end of the line are not connected.
- Straight - a continuous line without changes.
- Curve is not a straight line.
- Polyline - when segments are connected not at an angle of 180 degrees.
An infinite number of lines can be drawn through one point, but only one straight line and many curves can be drawn through two points.
Basic geometric shapes
Connected points form lines, and interconnected lines form basic geometric shapes on a plane.
Geometric figures are flat or two-dimensional (2D) and three-dimensional or three-dimensional (3D). They are bounded by the closed surface of their outer boundary.
If all points of a figure are in the same plane, then it is flat.
Flat figures that everyone knows: point, square, rectangle, triangle, circle, semicircle, circle, oval, rhombus, trapezoid.
And if all the points of a geometric figure are not in the same plane, then it is voluminous. These include a ball, cone, cylinder, sphere, pyramid, etc.
Let's analyze flat figures.
Triangle
Triangle is a figure that is formed when three line segments connect three points that do not lie on the same line. These three points are called vertices, and the segments are called sides.
There are three types of triangles:
- Rectangular - when one angle is right, the other two are less than 90 degrees.
- Acute - when the degree of its angles is greater than 0, but less than 90 degrees.
- Obtuse - when one angle is obtuse, that is, more than 90 degrees, and the other two are acute.
Triangles have the following properties:
- in a triangle opposite the larger angle lies the larger side and vice versa;
- the sum of the angles of a triangle is always 180 degrees;
- all angles of an equilateral triangle are 60 degrees;
- in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs (but this is already studied in high school).
The vertices of triangles are indicated by capital letters of the Latin alphabet: A, B, C, etc.
Examples of triangles:
Circle center distance.
Circle
The part of the plane inside the circle is called circle . That is, the circle is the boundary of the circle. And the distance from the center of the circle to any point on it is called the radius. The diameter of a circle is a line segment that connects two points on a circle and passes through its center. The diameter of a circle is equal to two of its radii.
Rectangle
Rectangle is a figure consisting of four sides and four right angles, in which:
- opposite sides are equal to each other;
- the diagonals are equal and bisect at the point of intersection;
- around a rectangle, a circle can be circumscribed with a center at the point of intersection of its diagonals and a radius that is equal to half of the diagonals.
-
Square
Square is the same rectangle with:
- all sides are equal;
- all angles are equal and equal to 90 degrees;
- diagonals are equal and perpendicular;
- The centers of the inscribed and circumscribed circles coincide and are located at the intersection point of its diagonals.
Trapezoid
0202 . If the sum of the lengths of the bases of a trapezoid is equal to the sum of the lengths of the sides, then a circle can be inscribed in it.
Parallelogram and rhombus
Parallelogram is a quadrilateral whose opposite sides are pairwise parallel.
Rhombus is a parallelogram with equal sides.
A parallelogram has the following properties:
- opposite sides and angles are equal;
- the sum of any two adjacent angles is equal to 180 degrees;
- the diagonals intersect and the intersection point is bisected;
- each diagonal divides the figure into two equal triangles.
Basic quantities and their formulas
All geometric figures have their own characteristics and their own value. The most common are such quantities as area and perimeter. They are used in everyday life, in construction and in other areas. For example, during renovation or new construction, the amount of materials needed and the scope of work cannot be determined without calculating the area and perimeter in advance.
Perimeter
The perimeter is the closed boundary of a flat geometric figure, which separates its inner area from the outer one. Any closed geometric figure has a perimeter:
In the figure, the perimeters are marked with a red line. The perimeter of a circle is often called the length.
The perimeter is measured in units of length: mm, cm, dm, m, km.
Designated by capital Latin P .
Area
Area is the part of the plane occupied by a closed flat geometric figure, that is, that part of the plane that is inside the perimeter.
It is she who gives us basic information about its size. Any flat closed geometric figure has a certain area.
In the figure, the areas of the figures are colored in different colors.
To measure the area of a figure means to find how many times another figure is placed in a given figure, taken as a unit of measurement. Area is measured in square units of length. Area units include: mm 2 , cm 2 , m 2 , km 2 , etc. S (square) - a sign of the area.
Perimeter and area calculation
Perimeter is the length of a closed contour of a geometric figure. You can, of course, measure the length of all sides with a ruler and add them. But it is better
to use special formulas for calculating the perimeter, this will greatly simplify the task.
- Square: perimeter = 4 * side.
- Triangle: perimeter = side 1 + side 2 + side 3.
- Irregular polygon: perimeter = sum of all polygon sides.
- Circle: circumference = 2 * π * radius = π * diameter (where π is pi (a constant approximately equal to 3.14), radius is the length of the segment connecting the center of the circle and any point lying on this circle , the diameter is the length of the segment passing through the center of the circle and connecting any two points lying on this circle).
To calculate the area of the figure, the corresponding formula is also required. Different formulas apply to different shapes. To calculate the area of standard geometric shapes, you can use the following formulas:
- Parallelogram: area = base * height
- Square: area = side 1 * side 2
- Triangle: area = ½ * base * height the center of the circle and any point on that circle (the square of the radius is the value of the radius multiplied by itself).
So, we have listed the main and most common geometric shapes and their properties.
The educational platform with iSmart smart simulators will help you introduce your child to these and other concepts, immerse yourself in the world of mathematics and it will not only be easy, but also very exciting.
Here on the simulator your child will learn the basic geometric shapes, their types, names and properties with the help of exciting tasks. Benefits of training on iSmart smart trainers:
- interactive tasks are more like a game;
- they can be practiced many times and will not be repeated;
- the system offers an individual training plan formed on the basis of knowledge diagnostics;
- Just 20 minutes of practice a day is enough to see progress in learning in a short time.
In addition, classes will help you free up your time, because the child will be able to study independently, and the parent will receive reports and monitor the dynamics of learning. The iSmart learning method is based on the latest scientific practices: microlearning with behavioral analysis.
