How to sort colors

The incredibly challenging task of sorting colours

Let’s start with something trivial: sorting numbers. Regardless of the algorithm you’ll use, real numbers are naturally ordered. Mathematically speaking, they have a total order, in the sense that you can always decide if a number is greater than another one. There is no ambiguity in this, meaning you can actually sort them, and (excluding duplicates) this sort is unique. There are other fields which are not that lucky: colour, for instance, are very unlucky. Supposing you’re representing colours with their RGB values, there is no standard way to order triples in a line, since they are naturally not organised in a line fashion. The problem is even more complicated since colours have a meaning in the real world. How can we sort colours so that they look as continuous as possible? Which parameters affects the sorting order? Is azure closer to blue (similar hue) or to cyan (similar luminosity)? I can stop you all here and say that there is no solution to this problem. You can sort colours, but the overall result depends on what you are trying to achieve. This post will explore how colours can be sorted, and how this can lead to very different results.

Part 1: Colour sorting

Let’s start by creating a bunch of random colours, sampling them from the RGB space.

import random  colours_length = 1000 colours = [] for i in range(1, colours_length): colours.append ( [ random.random(), random.random(), random.random() ] )

All the examples in this post will refer to this very list of random colours.

RGB sorting

The most trivial way in which we can sort colours is by directing sort its RGB values. Python has a very naive way of doing this: it sorts the first component, then the second and finally the third one. If two colours have the same quantity of red, the green channel will be used to determine which one is “bigger”.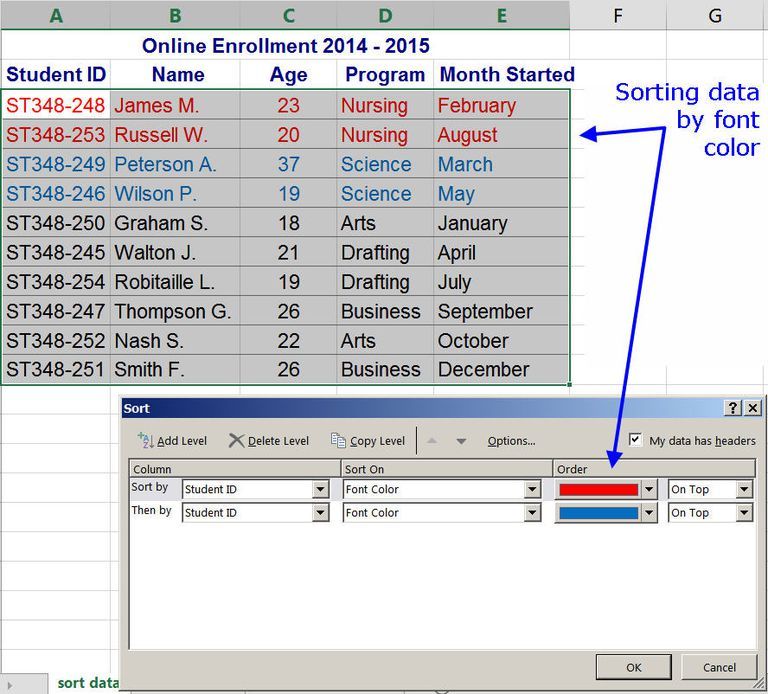

colours.sort()

The result looks indeed very poor.

HSV sorting

The RGB colour space works very well for monitors, but it does not represent how similar colours are. The HSV space attempts to overcome to this problem by introducing a parameter called hue. The hue is the base colour, made more intense or washed away by its saturation. The third component, simply called value, determined how “dark” the colour is. Since the hue has been arranged, by definition, in a rainbow fashion, sorting directly on the HSV values is likely to produce somehow visually pleasant results.

colours.sort(key=lambda rgb: colorsys.rgb_to_hsv(*rgb) )

Sorting using the HLS space, which organises colours in a similar fashion, produces seemingly indistinguishable results.

colours. sort(key=lambda rgb: colorsys.rgb_to_hls(*rgb) )

Both these solutions, however, looks very noisy.

Luminosity sorting

The reason why sorting in HSV and HLS colour spaces produces noisy result is caused by a single factor. HSV believes that hue is more important than luminosity. Two visually different shades of blue are closer, compared two two different colours with the similar intensity. An attempt to compensate for this is by sorting directly for the perceived luminosity of a colour.

def lum (r,g,b): return math.sqrt( .241 * r + .691 * g + .068 * b ) colours.sort(key=lambda rgb: lum(*rgb) )

But this, unfortunately, still yields a very poor result.

Step sorting

If we want to sort colours in a visually pleasant way, we need to do something more complicated. We can, for instance, merge hue and luminosity information to obtain a smoother result. Another problem we encounter, however, is determined by how tuples are sorted in Python. To dampen the impact that sorting on the first component has, we can reduce the colour space from a float value between 0 to 1, to an integer from 0 to 7. By doing this, much of the noise is removed.

def step (r,g,b, repetitions=1): lum = math.sqrt( .241 * r + .691 * g + .068 * b )  h, s, v = colorsys.rgb_to_hsv(r,g,b)  h3 = int(h * repetitions) lum2 = int(lum * repetitions) v2 = int(v * repetitions)  return (h3, lum, v2) colours.sort(key=lambda (r,g,b): step(r,g,b,8) )

Most of the noise is not removed, but the segments don’t look continuous any more. To fix this, we can invert the luminosity of every other segment.

def step (r,g,b, repetitions=1): lum = math.sqrt( .241 * r + .691 * g + .068 * b )  h, s, v = colorsys.rgb_to_hsv(r,g,b)  h3 = int(h * repetitions) lum2 = int(lum * repetitions) v2 = int(v * repetitions)  if h3 % 2 == 1: v2 = repetitions - v2 lum = repetitions - lum  return (h3, lum, v2) colours. sort(key=lambda (r,g,b): step(r,g,b,8) )

Colours looks now organised in a neater way. They are mostly continuous, with very little noise compared to the native HSV sorting. This, however, came at the expense of a monotonic luminosity. When it comes to colour sorting, we can’t have it all.

Hilbert sorting

There is another way to sort colours which looks rather interesting. It is based on the concept of Hilbert curve. You can image a Hilbert curve as a way of mapping every point in a 2D space by using a 1D curve.

This is possible because the Hilbert curve is a fractal space-filling object. We can extend the same concept of space-filling to our three dimensional colour space. What if we use a Hilbert curve to connect all the colours in their RGB space? For this example I am using Steve Witham‘s implementation of a Hilbert walk, as suggested by Jan Pöschko.

import hilbert colours.sort(key=lambda (r,g,b):hilbert. Hilbert_to_int([int(r*255),int(g*255),int(b*255)]) )

The result is indeed intriguing and, despite not following any intuitive colour distribution, it looks very homogeneous. It’s interesting to notice that while all the above mentioned technique would sort greyscale colours correctly, Hilbert sorting rearranges them in a very different way.

Travelling Salesman sorting

The travelling salesman problem refers to a very practical issues: visiting a certain number of cities minimising the overall distance and visiting each city only once. This sounds exactly what we want: visiting each colours only once, minimising the overall distance. Despite being such a critical issue, the travelling salesman problem is NP-complete, which is a fancy way of saying that is too computationally expensive to run over thousands of colours. The algorithm I’ll be using instead is a suboptimal version, called nearest neighbour. Without going too much into its details, it often finds solutions to the travelling salesman problem which are, on average, 25% worse. Which is not that bad, after all. I have used this version of the algorithm.

from scipy.spatial import distance # Distance matrix A = np.zeros([colours_length,colours_length]) for x in range(0, colours_length-1): for y in range(0, colours_length-1): A[x,y] = distance.euclidean(colours[x],colours[y])  # Nearest neighbour algorithm path, _ = NN(A, 0)  # Final array colours_nn = [] for i in path: colours_nn.append( colours[i] )

Its result is very smooth, even though the colours are all over the place. This solution, however, should be the one that really minimises the distances between them.

We can also use other colour spaces to calculate distance, such as the HSV (top) and the Lab (bottom) ones, although they all yields similar results:

Part 2: Colour distance

Colour sorting is deeply connected to another problem. Given two different colours, how distant are they? The concept of distance strongly depends on the space we are analysing them. Just to give you an indication, here there are some charts which will help you understand how distance is perceived in several colour space.

In the following diagrams, every (x,y) pixel indicates how distant the respective colours in the X and Y axes are. The X and Y axes arrange colours according to their hue value. White pixels indicate a perfect match: the colours have zero distance, meaning they are are identical. Dark pixels, instead, indicate a high distance. You can click on the charts to expand them.

HSV (& HSL)

RGB

YIQ

LAB

The next diagrams replace the rainbow colours on the horizontal axis with a greyscale gradient. There won’t be any white pixels since no two colours are the same now.

HSV & HSL

RGB

YIQ

LAB

Conclusion

Sorting by colours is a very common practice, especially in advertising and other form of media which requires to be visually pleasant. In a previous post I explained how I collected all the screenshots from #ScreenshotSaturday and sorted them, showing some interesting results over the predominant hues found in indie games. These mosaics are done using over 30.000 images, weighting almost 9Gb. You can download the full-size moisacs (16Mb, 71Mb, 40Mb, 13Mb) here on Patreon. Sceen size mosaics are also available in the tweet below.

Have you ever wondered what ALL the #ScreenshotSaturday submissions would look like together? @ScreenshotSat #gamedev pic.twitter.com/rnzd2PkP2c

— Alan Zucconi (@AlanZucconi) May 9, 2015

Sorting colours is a pain. There isn’t a magic function which will order them nicely, simply because the way we perceived them is based on three different components. Any attempt to flatten them onto one single dimension will inevitably collapse some of the complexity. When it comes to sort colours, you should understand which features you want to highlight. Is it the hue? Is it the luminosity? Start from there, and create your own function.

Other resources

Sorting colours with Hilbert curves: the post which inspired the Hilbert sorting;
Sorting colours in Mathematica: an interesting discussion on how colours can be sorted in Mathematica;
A Visit to Disney’s Magic Kingdom: how colour clustering and sorting can be used to identify emotions in Disney’s movies;
Using PCA to sort high dimensional objects: how to use Principal Component Analysis to sort colours;
TSPPixelSort: how genetics algorithms can be used to sort colours;
Rainbow Smoke: all the RGB colours sorted in a single image. It’s just beautiful.

Part 1: How to retrieve all the images from a website
Part 2: How to find the main colours in an image
Part 3: The incredibly challenging task of sorting colours

💖 Support this blog

This websites exists thanks to the contribution of patrons on Patreon. If you think these posts have either helped or inspired you, please consider supporting this blog.

Become a Patron!

Follow @AlanZucconi

📧 Stay updated

You will be notified when a new tutorial is relesed!

Email:

📝 Licensing

You are free to use, adapt and build upon this tutorial for your own projects (even commercially) as long as you credit me.

You are not allowed to redistribute the content of this tutorial on other platforms. Especially the parts that are only available on Patreon.

If the knowledge you have gained had a significant impact on your project, a mention in the credit would be very appreciated. ❤️🧔🏻

Sorting colors | CodePath Cliffnotes

Problem

Given N objects colored red, white and blue, sort them in-place in red-white-blue order.

Red, white, and blue objects are represented as 0, 1, and 2 respectively.

Example:

>>> colors = [2, 1, 2, 0, 0, 1] >>> sort_colors(colors) >>> colors [0, 0, 1, 1, 2, 2]

Approach #1: Merge or quick sort

Approach The problem is asking us to sort a list of integers, so we could potentially use an algorithm like merge sort or quick sort.

Time and space complexity With a sorting algorithm such as is O(N log N) in the worst case. The space complexity is O(1) since we sort in place.

Approach #2: Counting sort

Approach We know that the numbers we are sorting are 0, 1, or 2. This leads to an efficient counting sort implementation, since we can just count the numbers of each and modify the list in place to match the counts in sorted order.

Implementation

from collections import defaultdict def sort_colors(colors): counts = defaultdict(int) for num in colors: counts[num] += 1 idx = 0 while idx < counts[0]: colors[idx] = 0 idx += 1 while idx < counts[0] + counts[1]: colors[idx] = 1 idx += 1 while idx < counts[0] + counts[1] + counts[2]: colors[idx] = 2 idx += 1

Time and space complexity This solution has complexity O(N), since we loop through the list once, then loop through the dictionary to modify our list, both of which take N time. This solution takes up O(1) space, since everything is done in place and the counts dictionary has a constant size.

Approach #3: Three-way partition

This approach uses multiple pointers. Reading the two pointer guide may be helpful.

Approach Although we cannot asymptotically do better than O(N) since we need to pass through the list at least once, we can limit our code to only making one pass. This will be slightly faster than approach #2.

We can accomplish this by seeing that sorting an array with three distinct elements is equivalent to a partition operation. Recall that in quick sort, we partition an array to put all elements less than a pivot to the left and greater than to a right. Since we only have three potential values in our list, partitioning using the middle value as a pivot will effectively sort the list.

This particular type of partition is a bit tricky though because we're partitioning on the middle element (the 1's) of our list. It's called a three-way partition, since we are also grouping together elements that are equal in the middle (the 1's).

Implementation

def sort_colors(colors): left, middle, right = 0, 0, len(colors) - 1 while middle <= right: if colors[middle] == 0: colors[middle], colors[left] = colors[left], colors[middle] left += 1 middle += 1 elif colors[middle] == 1: middle += 1 elif colors[middle] == 2: colors[middle], colors[right] = colors[right], colors[middle] right -= 1

Time and space complexity This solution has also has complexity O(N), but only takes one pass since it uses two pointers that stop moving when one moves past the other.

It is slightly faster than the counting sort and is O(1) space, since it is in-place.

Note: This problem is also known as the Dutch flag problem.

How to properly sort clothes before loading into the washing machine?

August 24, 2020Answers

You asked, we answer.

You can listen to this article. If it's more convenient for you, turn on the podcast:

This question was submitted by our reader. You can also ask your question to Lifehacker - if it is interesting, we will definitely answer.

How do I sort clothes before putting them in the washing machine?

Zhyrgalbekov Elmurza

Evgenia Ovchinnikova

Housewife, author of the xtkani.ru fabric blog.

If you have a lot of clothes to wash, it is very important to sort them so as not to ruin anything. Here are five criteria to focus on.

1. Color

First of all, the laundry should be sorted by color - this is the most important point. For me it usually looks like this:

White and light gray - if you plan to add bleach or wash at high temperatures. Otherwise, I recommend even dividing this batch into two.
Black and dark blue. I usually wash this batch with a special gel for black clothes so that they retain their rich color.
Red and orange. I usually wash these two colors together: even if red fades a little, it will not be noticeable on orange. But if the red item is new and you have never washed it, it is better to separate the laundry to be sure.
Multicolored items in light shades: yellow, pink, blue, violet. But if the purple color is saturated, wash with blue things or separately.

Jeans should also be washed separately, because of the color, not the fabric. But if there are not many of them, sometimes blue and dark gray things can be added to them.

And remember: in parallel with sorting by color, it is necessary to check the pockets of each item so that there is nothing left in them that can ruin clothes, a washing machine, or spoil itself.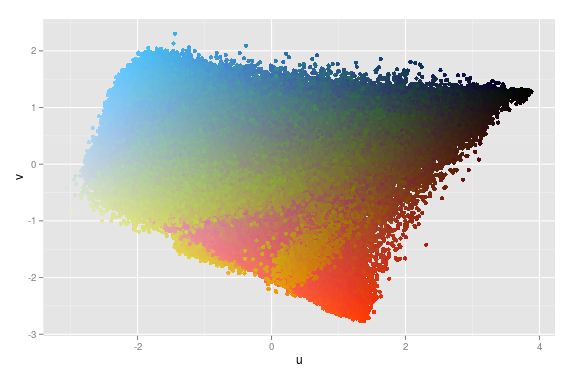 For example, a white batch of things may change color due to some red handkerchief forgotten in your pocket. These things cannot be recovered.

2. Wash cycle

Check the groups you have formed by color. Can they be washed under the same conditions, temperature and spin speed? If yes, then feel free to download it.

If in doubt, don't experiment! Divide the batches according to the washing cycle indicated on the tag, or simply wash the item in doubt by hand.

3. Degree of soiling

Each washing machine has a short 15-20 minute wash program that is suitable for items without serious soiling. It allows you to simply refresh them. In addition, very dirty things can ruin the rest. Therefore, always wash them separately: pre-soak and pay special attention to heavily soiled areas.

4. Weight

It is better to wash large items (plaids, bedspreads, bed linen, outerwear) separately from the rest of the laundry, otherwise the washing machine will turn things unevenly in the drum. At worst, it will break, and at best, you will get poorly washed clothes with stains from washing powder.

5. Type and accessories

Obviously, delicate fabrics and underwear should not be placed in the washing machine together with sweatpants in which you go for a walk with your dog. And it is better to wash children's things separately from things of adults.

For easy sorting and saving time, you can use special baskets with dividers and sort things into categories in advance. But my experience shows that each family member will have his own sorting principle and you still have to double-check.

Sort range by color

53901 11/10/2012 Download example

Method 1. If you have Excel 2007 or newer...

Everything is simple here.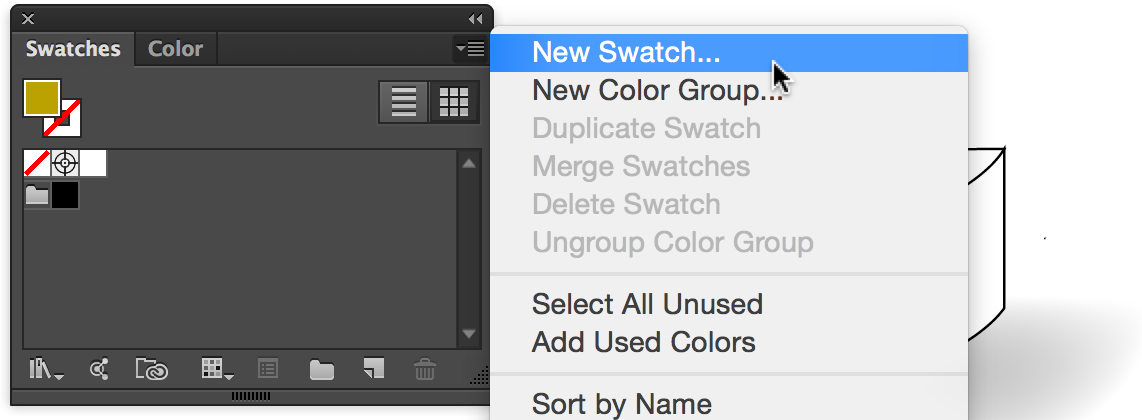 Starting from the 2007 version, Excel added sorting and filtering by fill color and font color as a standard feature. The easiest way to get to them is through a standard autofilter:

The only downside is the inability to filter by several colors at once.

Method 2: If you have Excel 2003 or later...

Versions of Microsoft Excel prior to 2007 in their original state were not able to sort cells by format, which is certainly a serious disadvantage if you use color coding in your spreadsheets (and this is convenient). Therefore, let's correct the annoying omission - we will write a simple user-defined function in VBA ColorIndex , which will output the numeric fill color code of any given cell. According to this code, we will further sort.

To do this, open the Visual Basic editor through the menu Tools - Macro - Visual Basic Editor (Tools - Macro - Visual Basic Editor) , insert a new empty module (menu Insert - Module ) and copy the simple text there functions:

 Public Function ColorIndex(Cell As Range) ColorIndex = Cell. Interior.ColorIndex end function

Now you can close the Visual Basic editor, return to Excel and, having selected any empty cell, call the created function ColorIndex through the menu Insert - Function - category User-defined (Insert - Function - User defined) . As an argument, specify the cell whose fill color you want to receive as a numeric code.

With regard to lists, this function will allow you to easily sort cells by fill color:

If you need to pull out not the fill color code, but the font color code, then the function will change slightly:

 Public Function ColorIndex(Cell As Range) ColorIndex = Cell.Font.ColorIndex end function

Our ColorIndex function unfortunately has a couple of drawbacks:

It can't get the color that a cell has when using conditional formatting
It is not automatically recalculated when the color of one of the cells is changed because Excel does not consider the color change to be an edit to the contents of the cell and does not trigger an automatic worksheet recalculation.
Learn more