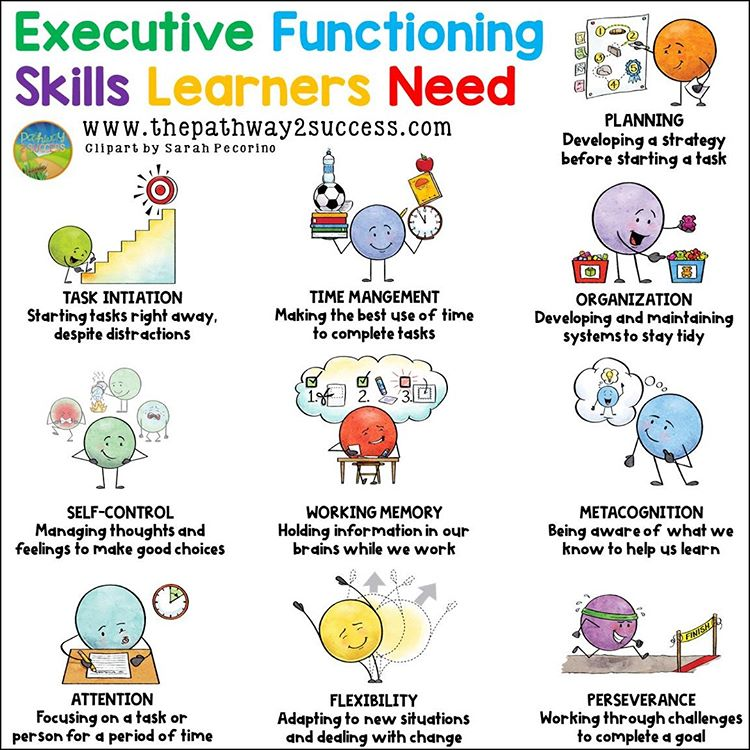
Most important math skills
Help Your Child Develop Early Math Skills
Before they start school, most children develop an understanding of addition and subtraction through everyday interactions. Learn what informal activities give children a head start on early math skills when they start school.
Children are using early math skills throughout their daily routines and activities. This is good news as these skills are important for being ready for school. But early math doesn’t mean taking out the calculator during playtime. Even before they start school, most children develop an understanding of addition and subtraction through everyday interactions. For example, Thomas has two cars; Joseph wants one. After Thomas shares one, he sees that he has one car left (Bowman, Donovan, & Burns, 2001, p. 201). Other math skills are introduced through daily routines you share with your child—counting steps as you go up or down, for example. Informal activities like this one give children a jumpstart on the formal math instruction that starts in school.
What math knowledge will your child need later on in elementary school? Early mathematical concepts and skills that first-grade mathematics curriculum builds on include: (Bowman et al., 2001, p. 76).
- Understanding size, shape, and patterns
- Ability to count verbally (first forward, then backward)
- Recognizing numerals
- Identifying more and less of a quantity
- Understanding one-to-one correspondence (i.e., matching sets, or knowing which group has four and which has five)
Key Math Skills for School
More advanced mathematical skills are based on an early math “foundation”—just like a house is built on a strong foundation. In the toddler years, you can help your child begin to develop early math skills by introducing ideas like: (From Diezmann & Yelland, 2000, and Fromboluti & Rinck, 1999.)
Number Sense
This is the ability to count accurately—first forward. Then, later in school, children will learn to count backwards.
A more complex skill related to number sense is the ability to see relationships between numbers—like adding and subtracting. Ben (age 2) saw the cupcakes on the plate. He counted with his dad: “One, two, three, four, five, six…”
Representation
Making mathematical ideas “real” by using words, pictures, symbols, and objects (like blocks). Casey (aged 3) was setting out a pretend picnic. He carefully laid out four plastic plates and four plastic cups: “So our whole family can come to the picnic!” There were four members in his family; he was able to apply this information to the number of plates and cups he chose.
Spatial sense
Later in school, children will call this “geometry.” But for toddlers it is introducing the ideas of shape, size, space, position, direction and movement. Aziz (28 months) was giggling at the bottom of the slide. “What’s so funny?” his Auntie wondered. “I comed up,” said Aziz, “Then I comed down!”
Measurement
Technically, this is finding the length, height, and weight of an object using units like inches, feet or pounds.
Measurement of time (in minutes, for example) also falls under this skill area. Gabriella (36 months) asked her Abuela again and again: “Make cookies? Me do it!” Her Abuela showed her how to fill the measuring cup with sugar. “We need two cups, Gabi. Fill it up once and put it in the bowl, then fill it up again.”
Estimation
This is the ability to make a good guess about the amount or size of something. This is very difficult for young children to do. You can help them by showing them the meaning of words like more, less, bigger, smaller, more than, less than. Nolan (30 months) looked at the two bagels: one was a regular bagel, one was a mini-bagel. His dad asked: “Which one would you like?” Nolan pointed to the regular bagel. His dad said, “You must be hungry! That bagel is bigger. That bagel is smaller. Okay, I’ll give you the bigger one. Breakfast is coming up!”
Patterns
Patterns are things—numbers, shapes, images—that repeat in a logical way.
Patterns help children learn to make predictions, to understand what comes next, to make logical connections, and to use reasoning skills. Ava (27 months) pointed to the moon: “Moon. Sun go night-night.” Her grandfather picked her up, “Yes, little Ava. In the morning, the sun comes out and the moon goes away. At night, the sun goes to sleep and the moon comes out to play. But it’s time for Ava to go to sleep now, just like the sun.”
Problem-solving
The ability to think through a problem, to recognize there is more than one path to the answer. It means using past knowledge and logical thinking skills to find an answer. Carl (15 months old) looked at the shape-sorter—a plastic drum with 3 holes in the top. The holes were in the shape of a triangle, a circle and a square. Carl looked at the chunky shapes on the floor. He picked up a triangle. He put it in his month, then banged it on the floor. He touched the edges with his fingers. Then he tried to stuff it in each of the holes of the new toy.
Surprise! It fell inside the triangle hole! Carl reached for another block, a circular one this time…
Math: One Part of the Whole
Math skills are just one part of a larger web of skills that children are developing in the early years—including language skills, physical skills, and social skills. Each of these skill areas is dependent on and influences the others.
Trina (18 months old) was stacking blocks. She had put two square blocks on top of one another, then a triangle block on top of that. She discovered that no more blocks would balance on top of the triangle-shaped block. She looked up at her dad and showed him the block she couldn’t get to stay on top, essentially telling him with her gesture, “Dad, I need help figuring this out.” Her father showed her that if she took the triangle block off and used a square one instead, she could stack more on top. She then added two more blocks to her tower before proudly showing her creation to her dad: “Dada, Ook! Ook!”
You can see in this ordinary interaction how all areas of Trina’s development are working together.
Her physical ability allows her to manipulate the blocks and use her thinking skills to execute her plan to make a tower. She uses her language and social skills as she asks her father for help. Her effective communication allows Dad to respond and provide the helps she needs (further enhancing her social skills as she sees herself as important and a good communicator). This then further builds her thinking skills as she learns how to solve the problem of making the tower taller.
What You Can Do
The tips below highlight ways that you can help your child learn early math skills by building on their natural curiosity and having fun together. (Note: Most of these tips are designed for older children—ages 2–3. Younger children can be exposed to stories and songs using repetition, rhymes and numbers.)
Shape up.
Play with shape-sorters. Talk with your child about each shape—count the sides, describe the colors. Make your own shapes by cutting large shapes out of colored construction paper.
Ask your child to “hop on the circle” or “jump on the red shape.”
Count and sort.
Gather together a basket of small toys, shells, pebbles or buttons. Count them with your child. Sort them based on size, color, or what they do (i.e., all the cars in one pile, all the animals in another).
Place the call.
With your 3-year-old, begin teaching her the address and phone number of your home. Talk with your child about how each house has a number, and how their house or apartment is one of a series, each with its own number.
What size is it?
Notice the sizes of objects in the world around you: That pink pocketbook is the biggest. The blue pocketbook is the smallest. Ask your child to think about his own size relative to other objects (“Do you fit under the table? Under the chair?”).
You’re cookin’ now!
Even young children can help fill, stir, and pour. Through these activities, children learn, quite naturally, to count, measure, add, and estimate.
Walk it off.
Taking a walk gives children many opportunities to compare (which stone is bigger?), assess (how many acorns did we find?), note similarities and differences (does the duck have fur like the bunny does?) and categorize (see if you can find some red leaves). You can also talk about size (by taking big and little steps), estimate distance (is the park close to our house or far away?), and practice counting (let’s count how many steps until we get to the corner).
Picture time.
Use an hourglass, stopwatch, or timer to time short (1–3 minute) activities. This helps children develop a sense of time and to understand that some things take longer than others.
Shape up.
Point out the different shapes and colors you see during the day. On a walk, you may see a triangle-shaped sign that’s yellow. Inside a store you may see a rectangle-shaped sign that’s red.
Read and sing your numbers.
Sing songs that rhyme, repeat, or have numbers in them.
Songs reinforce patterns (which is a math skill as well). They also are fun ways to practice language and foster social skills like cooperation.
Start today.
Use a calendar to talk about the date, the day of the week, and the weather. Calendars reinforce counting, sequences, and patterns. Build logical thinking skills by talking about cold weather and asking your child: What do we wear when it’s cold? This encourages your child to make the link between cold weather and warm clothing.
Pass it around.
Ask for your child’s help in distributing items like snacks or in laying napkins out on the dinner table. Help him give one cracker to each child. This helps children understand one-to-one correspondence. When you are distributing items, emphasize the number concept: “One for you, one for me, one for Daddy.” Or, “We are putting on our shoes: One, two.”
Big on blocks.
Give your child the chance to play with wooden blocks, plastic interlocking blocks, empty boxes, milk cartons, etc.
Stacking and manipulating these toys help children learn about shapes and the relationships between shapes (e.g., two triangles make a square). Nesting boxes and cups for younger children help them understand the relationship between different sized objects.
Tunnel time.
Open a large cardboard box at each end to turn it into a tunnel. This helps children understand where their body is in space and in relation to other objects.
The long and the short of it.
Cut a few (3–5) pieces of ribbon, yarn or paper in different lengths. Talk about ideas like long and short. With your child, put in order of longest to shortest.
Learn through touch.
Cut shapes—circle, square, triangle—out of sturdy cardboard. Let your child touch the shape with her eyes open and then closed.
Pattern play.
Have fun with patterns by letting children arrange dry macaroni, chunky beads, different types of dry cereal, or pieces of paper in different patterns or designs.
Supervise your child carefully during this activity to prevent choking, and put away all items when you are done.
Laundry learning.
Make household jobs fun. As you sort the laundry, ask your child to make a pile of shirts and a pile of socks. Ask him which pile is the bigger (estimation). Together, count how many shirts. See if he can make pairs of socks: Can you take two socks out and put them in their own pile? (Don’t worry if they don’t match! This activity is more about counting than matching.)
Playground math.
As your child plays, make comparisons based on height (high/low), position (over/under), or size (big/little).
Dress for math success.
Ask your child to pick out a shirt for the day. Ask: What color is your shirt? Yes, yellow. Can you find something in your room that is also yellow? As your child nears three and beyond, notice patterns in his clothing—like stripes, colors, shapes, or pictures: I see a pattern on your shirt. There are stripes that go red, blue, red, blue.
Or, Your shirt is covered with ponies—a big pony next to a little pony, all over your shirt!
Graphing games.
As your child nears three and beyond, make a chart where your child can put a sticker each time it rains or each time it is sunny. At the end of a week, you can estimate together which column has more or less stickers, and count how many to be sure.
References
Bowman, B.T., Donovan, M.S., & Burns, M.S., (Eds.). (2001). Eager to learn: Educating our preschoolers. Washington, DC: National Academy of Sciences.
Diezmann, C., & Yelland, N. J. (2000). Developing mathematical literacy in the early childhood years. In Yelland, N.J. (Ed.), Promoting meaningful learning: Innovations in educating early childhood professionals. (pp.47–58). Washington, DC: National Association for the Education of Young Children.
Fromboluti, C. S., & Rinck, N. (1999 June). Early childhood: Where learning begins. U.S. Department of Education, Office of Educational Research and Improvement, National Institute on Early Childhood Development and Education.
Retrieved on May 11, 2018 from https://www2.ed.gov/pubs/EarlyMath/title.html
Top 5 real world math skills to know before graduation
I was a college math major who does logic puzzles for fun, and I’m homeschooling a 14-year-old daughter who, until a couple years ago, cried at the mention of the subject.
Then there’s the other side of the coin: Maybe you’ve never been confident in your own math skills, so you’re having trouble knowing what your own children know (or don’t know).
It’s easy to get hung up on phrases like pre-algebra or probability, derivatives or decimals. And it’s not that those things are unimportant. But the more important part is the bigger picture: Do you, and do your kids, understand the how and why of the use of those things in the real world?
I can’t save the planet from mathematical mischief or leap tall buildings in a single bound (which, of course, is totally a physics equation). What I can do is share with you a few things a well-rounded person should know, mathematically speaking.
Unit price
This is the fancy way of saying “Which of these 57 packs of paper towels is the best buy?” It’s probably the most important real-world application of multiplication and division (and fractions) that I know. If you can get a 2-liter bottle of soda for $1.50 or a 1.5-liter bottle for $1, which would you choose?
This is something that is easy to get wrong. We tend to have a bias that a bigger pack is a better deal, and sometime is it – but not always.
Kitchen calculation
The recipe serves four, but you’re a family of five. What do you do? Fractions and proportions to the rescue!
This is one of the most straightforward examples of the “kitchen math” most people do. If you’ve just dirtied the half-cup measure with oil and you need another half-cup of flour, you can fill your quarter-cup measure twice. Most of us do this without even thinking, but it’s an important skill to talk about. My daughter is an incredible example of this. She had no idea as of a year ago that two fourths were the same as one half – or to be fair, if she did know that in theory, she had no idea that it translated into the process of cooking!
Inverse operations with money
These come in several forms, with two being particularly important: Making change and balancing a checkbook.
The inverse concept is often a hard one to grasp. If you’ve written all your transactions in your check register and there’s a check that has not yet cleared the bank, how do you know if you show the same balance they do? You add that amount back to your calculated balance. That’s an inverse operation, and it’s something many people struggle to grasp conceptually!
The same goes with making change. If I give you $20 for a $4.50 product, it’s so much quicker to do the inverse operation – to “count up” from the cost, not subtract from the payment amount. But it runs contrary to the way many of us think!
Cost per use
I own a $300 purse that was one of the most economically sound purchases I ever made. Why? Cost per use. If I use this purse every day for a year, my investment is less than $1 per day – about 82 cents. I’m now on my third year, which has put me at about 20 cents per use.
I used to buy $30 to $50 purses that would last me maybe three or four months before getting holes or broken straps or big stains.
Even at best, my cost per use on those was no lower than 25 cents, usually almost double. Add in the cost of my time shopping for them, and suddenly, I’m better off with the “nice” one in the first place!
It might sound silly to break down every purchase like this. But teaching your children that cheap and economical are NOT always the same is an amazing start into real-world consumer finance!
Interest and debt
This is another area in which your openness with your kids will be rewarded. No matter how you feel personally about credit cards – if you’re 100% OK with them or 100% against them – make sure your children know how interest and loaned money work.
If you borrow money, it must be repaid eventually, and generally with interest. The longer you take to repay what you owe, usually the more interest you will pay on top of the original amount.
Do your children understand how the “business” of money works – and how they can either gain or lose money as part of it? Have you talked with them about what a bank does with your money – and how you can sometimes earn money by “loaning” yours to the bank temporarily?
Real world math matters!
Maybe these skills don’t seem “complex enough” for high-school math.
I assure you, though, they are – and digging into them with your family, looking at how you put everything from pre-algebra to calculus in action, is going to position your children to succeed with real-world math!
More great resources for homeschooling and unschooling math
This post is also part of the iHomeschool Network’s Massive Guide to Homeschooling Math.
Click the image to read many, many more posts full of great math advice!
Also, if you’re into the things we do in our family homeschool, check out my previous “5 days of…” series, 5 days of real-world math.
Warning: Undefined variable $tag_list in /srv/unschoolrules.com/wp-content/themes/unskooled/content-single.php on line 54
Warning: Undefined variable $tag_list in /srv/unschoolrules.com/wp-content/themes/unskooled/content-single.php on line 65
This entry is about curriculum, homeschooling, math, parenting, unschooling.
12 simple tips for self-taught math
The article describes effective strategies for learning the concepts of higher mathematics, which will be useful to those who teach mathematics on their own.
We all wish we were better at math. Many of the tips below will be useful to those who teach mathematics and not only.
Mathematics is not only and not so much a subject of the university curriculum, but a powerful language for representing abstract ideas. With the help of strict, consistent sets of rules, mathematics allows any concept to be given a concrete form.
These rules must be treated with respect, because they have been developed over a long period of time by the best minds. Your mind must be open to this: blind memorization will not produce results. Memorization of mathematical facts by those who teach mathematics usually occurs naturally in the course of repeated use of previously learned fundamentals.
Although many people have a fear of mathematics, research shows that the student's perception of his own intellect as a developing object leads to good learning dynamics. That is, first of all, you need to believe in your own strength.
Mathematics is available to everyone. You can learn anything if you have the right motivation.
Don't worry if you don't understand a math concept right off the bat. It has been proven that the brain develops even when you make mistakes. Do not worry if someone finds it easier to solve problems. Most often it is only a matter of experience and discipline of the mind. Our selection of books and courses will help you wake up the math in you.
If you are self-taught math, start with areas that interest you personally. Don't waste time on boring (but seemingly necessary) topics.
Many of those who taught or are still learning mathematics have faced a similar situation. What is uninteresting at a particular moment within the framework of the current stage of learning becomes understandable and even fascinating later on after going through topics that are now interesting. An interest may develop out of a need for a certain type of knowledge. If you are into artificial intelligence, you will immediately understand where linear algebra, probability theory, etc.
come in handy.
Try to focus on only one topic within the allotted time frame. It is better to switch between global areas, rather than adjacent mathematical concepts.
The material that you constantly use is fixed in memory. It will be useful to remind once again that learning is not one of those things that are done at a time by one effort of will. If you do at least a little every day, the brain perceives what you are learning not as an accidental event, but as material necessary to make life easier. This leads to a more successful assimilation of the material than intentional memorization.
If you need reference material, such as a selection of formulas, use thematic guides. Including brief ones - the same cheat sheets that are easy to find on the request "[the topic under study] cheat sheets".
Mathematics requires solving problems. And, of course, it is better if these are tasks that are not boring to solve. Great work has been done on brilliant.org to collect materials from various areas of mathematics, presented in various styles of presentation.
If a task is too long to solve, leave it and start again later. Go back to it until you decide, but don't spend too much time at one time. At some point, the brain will learn enough on other tasks to solve a more complex one.
If you feel that you have reached a dead end, do not hesitate to ask for help, including on the Internet - from those who are still studying mathematics or are already experts. Seeing the situation with different eyes, you will discover previously unfamiliar sources of approaches to the solution.
Practice every day, but not for too long, take breaks. Keep a balance of mental work and rest. Do not neglect respite and switching thoughts to other things. At such moments, imperceptibly for you, the brain continues to process and assimilate information.
It is very important to warm up. Nutrition to the brain tissues carries blood, and if the blood flow is difficult, it is more difficult to learn. Make it a rule to warm up every 45-50 minutes: walk around the room, squat, do exercises.
So that the blood can be saturated with oxygen, exercise in well-ventilated areas.
A change of scenery is also important. After working out for half a day, go for a walk or exercise, do your homework. After studying for a week, go to rest in the countryside. A change of scenery gives a feeling of freshness, gives a fresh look at the tasks being solved.
Do not neglect nutrition. It must be balanced. Thought processes belong to the group of the most energy-intensive tasks solved by the human body. You can "motivate" the brain with small snacks after solving a predetermined number of tasks, evenly splitting meals depending on the number and difficulty of tasks. Eat more omega-3 polyunsaturated fatty acids - they directly affect the concentration of thinking and brain activity. Drink enough water.
Avoid stress. One of the most common types of stress for the body is lack of sleep. Lack of sleep catastrophically reduces mental performance. It helps to recover not only at night, but also a short sleep during the daytime.
For math learners, there are many tools available to gamify the process. Among the best known are the video games Variant: Limits and while True: learn(), where learning takes place through puzzle solving.
If you are interested in how mathematics is used in the development of popular games, check out our article.
When studying mathematics, it is important to be in a continuous stream of thought. New visual abstractions and solutions can be gleaned from watching videos on various mathematical topics. To do this, we have prepared a selection of 7 useful Youtube channels.
Take notes in such a way that you get lecture notes that someone who does not understand the topic at all can learn from. A good methodological solution for taking notes is an approach that can be jokingly called by the first letters as AD POT: Analogy, Diagram, Example, Explanation, Term.
- Analogy. First ask yourself: have I seen something similar before? For example, the concept of electrical resistance is similar to the concept of fluid movement in a pipe.
Connect the acquired knowledge with previously known ones, include them in the existing picture of the world. Memorization by associations is more efficient, while isolated knowledge is removed first by our internal system of "garbage cleaning". - Chart . Visualize the concept. A concrete image should appear before your eyes, on which you can rely in further reasoning. It can be a picture, a list of elements, a table, a mindmap, etc.
- Example . Consider a specific example of using the concept, try to solve the problem, get the first experience in applying the material.
- Description . Describe the concept in your own words: what it is and what it is for.
- Termin. Finally, give a strict technical definition that links the concept to other terms. This formalizes understanding and allows you to communicate with specialists in the same language.
When taking notes, write and draw, but do not type.
The use of motor skills stimulates our creativity and allows the brain to better absorb the material. If you are afraid of losing your records, scan them.
The following advice will be useful to those who have difficulties with "local" motivation, that is, students who find it difficult to conduct classes systematically, with the same frequency.
Taking a break for rest, do not try to come to a logical conclusion of the topic. Make full use of the specific time that you decide to spend on the lesson, but as soon as it has expired, immediately stop. The ideal option is to approach the peak of the topic. This advice is based on several psychological premises.
Firstly, classes in this form have a strictly defined framework. You won't wear yourself out and waste your time. And, therefore, you will be more enthusiastic about classes.
Secondly, it will be easier for you to get into a working rhythm by starting the next session. By refreshing your knowledge a little, you can quickly tune your brain to new activities.
In the case when the beginning of a new topic coincides with the beginning of the lesson itself, additional efforts are required to delve into it. This is the most difficult place, which is best taken with overclocking.
Third, when you get into the habit of thinking about mathematical abstractions regularly, this approach will help develop mathematical intuition. Despite the fact that you interrupted the lesson, the brain will continue to work and build a logical chain of thoughts on its own, without the support of educational material.
What gets measured gets improved. Create a study plan with milestones. Such frames increase concentration. You kind of become your own leader, issuing instructions. Both those who teach mathematics and those who teach.
Examples of such plans: a long-term plan for studying Computer Science or a more specialized plan for Deep Learning and Neural Networks.
Many scientific studies have shown that teaching and learning together can improve learning.
In order to convey a thought to another person, it must not only be read, but also understood. This gives additional motivation, as it imposes obligations on you. Working in conjunction with a friend or a student, it becomes easier for both of you to motivate yourself to periodically practice.
In extreme cases, you yourself can become a listener. Explain the topic covered from beginning to end to an imaginary student. You will see that from this angle you have been able to realize it more deeply. This approach obliges to understand all obscure places.
- Mathematics for a programmer: tips, sections, literature
- Math for programmers: 7 cool YouTube channels
- 4 books that will awaken the math in you
- Mathematics in game development: how it is used and what to read on the topic
- Illustrative video course of mathematical analysis: 10 lessons
- Illustrative video course in linear algebra: 11 lessons
- What a programmer without specialized education should know
- Method of learning mathematics used in Oxford
- 13 resources to learn math
- Top 40 Math Courses for Programmers
definitions, examples and how to improve them • BUOM
Posted by the Indeed editorial team
July 12, 2021
From calculating financial transactions to measuring spaces and objects, math skills are an important part of everyday life.
Improving basic math skills can help you get a job, perform better in your current position, and make it easier to manage your personal life. In this article, we will discuss basic math skills, how you can improve them, and how having basic math skills can improve your job search.
What are basic math skills?
Basic math skills are those that involve calculating sums, sizes, or other measurements. Basic concepts such as addition, subtraction, multiplication, and division provide a foundation for learning and using more advanced mathematical concepts. Having basic math skills will help you both at work and in everyday life.
Related: Math Skills: Definition, Examples and How to Develop Them
Addition, Subtraction, Multiplication and Division
To do anything related to mathematics, you need to know how to add, subtract, multiply, and divide basic numbers. Knowing these basics is extremely helpful, especially when dealing with money. For example:
Addition: You and two of your colleagues pay $5 each for a $15 pizza: $5 + $5 + $5 = $15.
Subtraction: You and two co-workers share a $15 pizza. You and one employee are paying and want to determine how much a third employee owes: $15 - $5 + $5 = $5.
Multiply: You and two colleagues each have $5 for a pizza and you want to know how much pizza you can afford: $5 x 3 = $15.
Division: You and two employees share a $15 pizza for lunch, and everyone wants to pay their share. You would use division to calculate the cost: $15/3 = $5 each.
Read more: Counting Skills: Definition and Examples
Percentage
Percentage is 100 times the whole. strength. For example, you invited a business partner to dinner and the bill was $50 plus $8 in taxes. You want to leave a 20% tip for good service. In this case, it would be $10 based on $50.
Related: How to Calculate a Percentage
Fractions and Decimals
Fractions are part of a whole number, and a decimal is the numeric representation of that fraction. For example, $1 can be divided into quarters (a fraction represented here as 1/4) or 25 cents.
In another example, the box contains 12 widgets, but the customer only wants six, or ½ of the box. The whole package will be 1.0 in decimals and half will be 0.5. Additional basic decimal skills include rounding to the nearest tenths or hundredths and mental estimation of values.
Related: How to divide fractions: tips and tricks to use
Visual representation of data
Often numbers are presented in visual formats. The basic math skill that needs to be mastered is reading and understanding charts and graphs. Being able to read the axes, trend line, and data points will help you gain a deeper understanding of the underlying data. It will also help you make graphs and charts to better illustrate your points.
Unknown solution
Solving an unknown variable is a basic problem in algebra. Algebra is a branch of mathematics in which letters and other symbols are used to represent numbers and quantities in a formula or equation. A variable is a literal character (A, B, etc.
) that represents a number in an equation. The solution for the unknown can be as simple as B = 20 + 20. The unknown variable (B) is the sum of the two numbers, or 40.
For example, Juan needs to earn $600 this month and he makes $20 each time when walking the dog for one of his neighbors. The "unknown variable" Juan wants to solve is the number of dog walks he needs to earn the required amount. With basic algebra skills, Huang would be able to create a simple formula for this equation (20 x Y = 600) and find the unknown variable Y.
Related: 50 jobs that use algebra
How to improve your basic math skills
There are four main ways to improve your basic math skills:
are a great way to practice your basic math skills. Often, math workbooks contain instructions and tips for solving problems, as well as answers so you can check your work. If there is a particular topic in math that you find difficult, look for a math textbook that focuses on that math skill.
2. Take a lesson
Basic math classes are offered both online and usually at local colleges and study centers and can be extremely helpful in improving your understanding of basic math concepts. . The advantage of math classes is that they provide more detailed instruction and the opportunity to ask questions if you are unsure about a topic.
3. Ask for help
If you know someone who is good at math, ask them for help. Let them know which areas you find difficult and see if they have any advice. Friends, family members and colleagues can provide a new perspective or perhaps explain things in clearer terms than the average instructor.
You can also hire a tutor to give you one-on-one attention in person or online. They can give examples of tasks to help you improve your skills and answer any questions you might have.
4. Practice
The best way to improve your basic math skills is to practice. Constant use of your skills can ensure that you retain your skill.
Try not to use a calculator for every problem you face and don't ask someone else to calculate a math problem for you. Take every opportunity to use your basic math skills and they will get stronger over time. What's more, many industries and professions require math testing before being considered for jobs, so it's always a good idea to keep your math skills strong.
Basic math skills in the workplace
Here are just a few examples of how you can use basic math skills in the workplace:
Calculating taxes
Knowing how to calculate taxes is vital to running a financially stable business. You need to know how to calculate sales tax, income tax, property tax and more. While there are tools to help you calculate various taxes, knowing how to get these numbers will help you better understand your financial situation and avoid financial mistakes.
Giving presentations
Business leaders often make decisions based on data. If you are making a presentation, you should be able to back up your statements with facts and figures.
Knowing how to create various graphs, charts, and charts to explain and present your numerical results, as well as how to understand them in front of other people, is a common requirement in the workplace.
Read more: 6 types of presentations to use in the workplace
Payroll and allowances
As an individual, if your salary is $60,000 a year, you'll want to know how much your weekly salary will be. Also, if your boss gives you a 10% raise, you'll want to know how much extra income that is. Being able to count the numbers that matter most to you will help you make better decisions about where to work and how much you can afford to spend on your personal life.
Related: How to Calculate Gross Wages with 9 Examples0003
Time Estimate
You can use your basic math skills to plan tasks. For example, you have a project that consists of 10 equal parts. You have already completed three parts in nine days. When your manager asks how long the rest of the project will take, you can use basic math skills to give them an estimate of three days per task, or 18 work days in total.
Read more: 6 ways to optimize your daily routine
How to Highlight Basic Math Skills
Here's how to highlight your math skills in a job application:
On your resume
To highlight your basic math skills on your resume, give real-life examples. For example, if you are a cashier, instead of saying that you are good at adding and subtracting, you could say:
-
Able to quickly calculate the change the customer owes in my head.
You may also refer to your basic math skills in your job description. For example, a marketer might write:
-
Created clear data visualizations to demonstrate the effectiveness of various marketing campaigns.
The goal is to emphasize your use of basic math skills, not to point them out. You can do this in any section, for example, work experience, special skills, or even in a cover letter.
At a job interview
During an interview, you may be asked to demonstrate some of your basic math skills.
