Instructional strategies for teaching letter recognition

Tips and Activities for Teaching Alphabet Recognition

Alphabet recognition is one of the first skills children learn as beginning readers. In this post, I’m sharing 4 strategies for teaching letter recognition, as well as digital and printable alphabet recognition activities for kindergarten and preschool students.

If you work with young students I know you spend a lot of time working with them on letter recognition. It is one of the very first skills children learn as beginning readers. It’s so important because it allows them to see how printed text is related to our spoken language.

As with any new skill, in order to master letter recognition students must have LOTS of opportunity for practice and review. We also know that children learn the alphabet best through a combination of direct instruction and multiple exposures to print. The good news is there are TONS of great ways to teach alphabet recognition!

It would be easy to spend hours gathering ideas from the internet, planning and prepping your alphabet activities…. But I’ve taken all of that off your hands! Today I’m happy to share 4 strategies for teaching letter recognition and activities to go along with each one!

Note: There is no general consensus on the best sequence for teaching the alphabet. I recommend introducing the activities in the order they are presented below.

So let’s take a look….

1. Teach Children the Letters in Their Name

Starting with name activities makes a lot of sense! For one, most children are already familiar with the way their name looks which gives you a good starting block. It also makes sense to start with name activities at the beginning of the school year when you are all getting to know each other!

You can start by just identifying and naming the letters. Once the letter name mastery is apparent, you can move onto the sounds each letter makes. The good news is that most letters in names are closely related to their sounds. This helps to make the alphabetic principle (the idea that each letter stands for a sound) pretty clear to kids!

I love these editable name activities because they develop fine motor skills while at the same time help young learners recognize, learn to spell, and write their names.

All too often activities that involve student names require you to hand print each individual name for every activity, but not this resource! Instead, it has been created as an editable “autofill” document so you can personalize each page for your students in no time at all! It’s so simple. Once you type your students’ names into the class list, you simply print the pages that you want to use. Take a look at this quick demo video below to see how this resource will literally save you HOURS of work!

Another perk of this resource is that it naturally meet the needs of all different learners. There are 9 different activities included that range from identifying letters of their name to writing it. Students who are ready to take on more of a challenge can benefit from recognizing and working on their last names or their classmates’ names.

2. Teach the Shapes of Letters and Provide LOTS of Practice

Children need A LOT of practice writing letters (as early as possible) in order to learn the letter shapes. When children are taught to write letters accurately and encouraged to pay attention to their distinctive features, it significantly helps with their letter recognition, (Clay, 1993).

According to Wiley Blevins’ book, Phonics from A-Z, if you’re working with kids who have limited alphabet knowledge, don’t teach them both uppercase and lowercase forms of the letters at the same time. If children are in preschool, focus on uppercase first. Uppercase letters are easier to distinguish visually. If you are working with kids in kindergarten or first grade, focus on lowercase letters because that is what they most frequently encounter in text.

Independent writing is the most effective way to teach children to form the shapes of each letter, but copying and tracing can also be useful. Blevins recommends encouraging students to say the letter name and/or sound as they trace it. Tracing and copying also help to develop fine motor skills.

This resource is a WONDERFUL way to teach children correct letter formations. It is highly engaging for students and NO PREP for you!!!

Each letter slide starts with a letter introduction video students get to watch (and sing along to). Then they get to view a super helpful animated printing GIF that demonstrates the correct way to form the letter.

Finally, there is a worksheet for every letter where students identify, trace, and write the letter. This resource is made for virtual or in-person learning and is the perfect resource for morning work, literacy centers, or homework!

I love this resource because it is a one stop shop for practice with fine motor skills, hand-eye coordination, and proper alphabet letter formation. Students LOVE the hands-on aspect of the letter tracing activities.

The resource includes 5 different alphabet activities so students never get bored of doing the same thing over and over again. This resource makes engaging, EASY to PREP literacy center activities.

There are 2 versions of each alphabet activity included in this resource to help you best meet the needs of your students.

This fine motor alphabet activities bundle includes:

TRACE, BUILD, WRITE IT ALPHABET ACTIVITIES
PAINT IT ALPHABET ACTIVITIES
FILL IT ALPHABET ACTIVITIES
DOT IT ALPHABET ACTIVITIES
LETTER IDENTIFICATION ACTIVITIES

While we generally want our young students to engage in hands-on activities, in this time of virtual learning and social distancing, this digital resource is a GREAT option. It is a digital resource that helps students to learn to recognize alphabet letters, form upper and lowercase letters, and practice the sound of each letter.

You’ll love this resource because all of the activities are NO PREP for you! Each one has been PRELOADED, so with 1 click you can add them to your Seesaw library or Google drive. Then all you have to do is assign them to your students!

For each letter there are 10 consistent activities. Once you teach the procedures and expectations for the first activity, you can be confident your students will know how to independently complete the rest of the tasks.

These alphabet activities are perfect for students to work on during independent learning centers or at home learning.

Activities included in the alphabet bundle:

ALPHABET ORDER
LETTER FORMATION
UPPER/LOWERCASE LETTER SORTS
ALPHABET RECOGNITION MAZES
MAKE & READ ALPHABET WORDS
VISUAL LETTER DISCRIMINATION
ALPHABET PICTURE SOUND SORTS
UPPERCASE LETTER BUILDING
LOWERCASE LETTER BUILDING
ALPHABET SENTENCES

Alphabet books are wonderful because they provide opportunities for students to hear, see, say and write the alphabet in a variety of contexts and for different purposes.

They are also helpful in the following ways:

🍎 Alphabet books help beginning readers’ to develop their oral language, the skills and knowledge that go into listening and speaking. This development is essential for reading comprehension and writing.

🍎 Alphabet books are presented in ABC order which helps students to learn their letter sequence.

🍎 As they listen students learn to associate an individual sound with an individual letter.

🍎 Alphabet books help to build vocabulary and world knowledge. This is especially helpful for English language learners or those with limited world knowledge.

🍎 Finally, alphabet books are fun and engaging! They usually don’t have a lot of text and therefore can be more appealing to readers who may be intimidated by books with more text.

You can read more about how to use alphabet books in the classroom and download a FREE list of alphabet mentor texts here.

4. Include Multi-Sensory Alphabet Activities

Tactile, visual, auditory and kinesthetic (movement) activities are great for teaching the alphabet- and of course, young children love them.

In his book, Blevins shares a list of 35 different multi-sensory activities for developing alphabet recognition. Some of my favorites from his list include:

💗 Body letters: Divide the class into groups of three to five students and assign each group a letter to form with their body or bodies.

💗 Letter Pop-up: Distribute letter cards, one or two to each child. Call out a letter. Those holding that letter “pop up” from their seat. This is a great activity when you have a few extra minutes to spare and a nice way to quickly check for accuracy.

💗 Letter Actions: Teach an action for each letter they learn. As you introduce the letter, model the action and have the students perform it. In later weeks, you can hold up letter cards and the students can do the action associated with it.

💗Alphabet walk: Take the kids for a walk around the school or neighborhood. Have them look for and identify letters they can find in environmental print.

Finally, if you’re looking for ONE single resource that has ALL YOU NEED to teach letter recognition you’ll want to take a look at my Alphabet Activities Bundle.

This bundle includes 11 different engaging and interactive digital and printable worksheet alphabet activities. It’s the perfect bundle for preschool and kindergarten students who are learning to recognize alphabet letters, form upper and lowercase letters, and practice letter sounds!

I hope the information and resources I’ve shared today will help to save you time and bring more engaging alphabet recognition activities into your classroom!

-SHOP THIS POST-

–PIN for LATER–

Alphabet Matching | Classroom Strategies

Very young learners are developing their understanding of the alphabetic principle — the understanding that there are systematic and predictable relationships between written letters and spoken sounds. Teachers can help students develop this understanding through lots of fun activities that help students explore the alphabet letters and sounds.

How to use:

Individually

With small groups

Whole class setting

More phonics strategies

Why teach about the alphabet?

Letter naming is a strong predictor of later reading success
Learning letter names helps a child learn letter sounds
It helps students develop their understanding of the alphabetic principle

Watch: Alphabet In My Mouth!

Students practice each letter-name, sound, and corresponding action to help solidify letter-sound correspondences in an active and engaging way — with a song. See the lesson plan.

This video is published with permission from the Balanced Literacy Diet. See many more related how-to videos with lesson plans in the Letter-Sounds and Phonics section.

Collect resources

Matching upper-case and lower-case

Teachers can use the following activity to ask students to help the "Mama animals" (uppercase letters) find their "babies" (lowercase letters). This game includes matching the uppercase mothers with their lowercase babies. See example >

This link provides a template for a printable "Superhero" upper- and lowercase letter match game. See example >

This file includes uppercase and lowercase letters in a matching game that parents can use with their child at home. See example >

This link provides templates for printing cards to use for writing uppercase and lowercase letters. See example >

Letter formation: using sand, play dough, or flour

This link provides teachers with downloadable mats with the alphabet letters for helping children use play dough for learning letter formation. See example >

Letter bingo

Bingo is a simple game that children enjoy and can be used to help them learn about the upper- and lowercase letters. This link allows teachers to print the letters and board needed to play letter bingo. See example >

Letter stamps

Stamps are an excellent "hands-on" activity for helping students learn about the alphabet. The activity described in the link below provides teachers with some creative ideas for making letter stamps out of sponges. Teachers can use sponges and paint in a variety of ways to help children understand the shape and function of upper- and lowercase letters. See example >

Letter recognition fluency

This online document contains several activities that are helpful for building letter recognition fluency. Teachers can download materials needed and follow the instructions for each activity. There are also some ideas included for extending and adapting each activity to further enhance learning. Some examples are provided below. Download activities >

Speedy Alphabet Arc: Teachers can download and print a copy of the alphabet "arc" and have students use letters to match the ones on the arc. Parents could use this idea at home with magnetic letters by placing the arc on the refrigerator and have the child match the letters. Using a timer and seeing how quickly the child can match the letters is optional.

Glow Go: This activity includes the use of glow in the dark chalk and black construction paper. Students can work together taking turns using a flashlight and naming the letters.

Hungry Letter Mouse: Teachers can utilize this activity for students to work on letter recognition in pairs using an eraser and dry erase marker. One student can use the eraser to be the mouse and the other student names the letter before the "mouse" eats it (i.e., erases it).

Letter books

Teachers can use the downloadable materials form this website to create letter books in which each page contains one letter. The kids draw or cut pictures from magazines that start with the particular letter and glue them into their "book." See example >

Downloadable letter and alphabet cards

Flash cards

The link listed below provides teachers with downloadable ESL flashcards. These are free and printable for use within the classroom. There are large sets for use with teaching letters and vocabulary, and smaller sets for language learning games. See example >

This website provides printable color flashcards that are great for teaching upper- and lowercase letters. These cards are free and use the Zaner Bloser font which is very simplistic — ideal for teaching young children.

See example >

Alphabet cards

The downloadable alphabet cards available from this link have various fonts to choose from, color picture cards to accompany the letters, and creative ideas for activities. See example >

Race track alphabet

The website below offers teachers the ability to download letters of the alphabet in race-track format. Children can use toy cars to trace around the letters to help learn the formation. See example >

Differentiated instruction

for Second Language Learners, students of varying reading skill, and for younger learners

Begin with a very simple, plain alphabet font like Zaner Bloser. As children become more familiar with letter shapes, progress to different fonts that may present letters slightly differently. For example, consider how the letters /a/, /g/, /t/ appear in different fonts.
Decide how many letters a child or group should work with at one time. Very emergent learners should begin with fewer letters; other students can manage working with more letters at one time.
Just for fun! Serve alphabet soup or use Alpha-bits cereal as an extra reinforcement of letters.

See the research that supports this strategy

Adams, M. (1990). Beginning to read: Thinking and learning about print. Cambridge, MA: MIT Press.

Articles on the topic of what artificial intelligence is have been written for a long time. And here is the mathematical side of the coin :)

We continue the series of first-class illustrative courses 3Blue1Brown (see our previous reviews on linear algebra and math analysis) with a course on neural networks.

The first video is devoted to the structure of the components of the neural network, the second - to its training, the third - to the algorithm of this process. As a task for training, the classical task of recognizing numbers written by hand was taken.

A multilayer perceptron is considered in detail - a basic (but already quite complex) model for understanding any more modern versions of neural networks.

The purpose of the first video is to show what a neural network is. Using the example of the problem of digit recognition, the structure of the components of the neural network is visualized.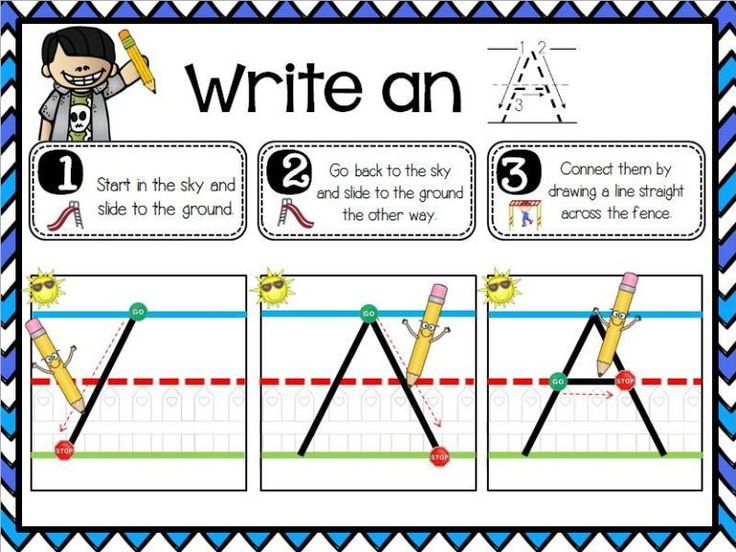 The video has Russian subtitles.

Number Recognition Problem Statement

Let's say you have the number 3 drawn at an extremely low resolution of 28x28 pixels. Your brain can easily recognize this number.

From a computational standpoint, it's amazing how easy the brain is to perform this operation, even though the exact arrangement of the pixels varies greatly from one image to the next. Something in our visual cortex decides that all threes, no matter how they are depicted, represent the same entity. Therefore, the task of recognizing numbers in this context is perceived as simple.

But if you were asked to write a program that takes as input an image of any number in the form of an array of 28x28 pixels and outputs the “entity” itself - a number from 0 to 9, then this task would cease to seem simple.

As the name suggests, the device of the neural network is somewhat close to the device of the neural network of the brain. For now, for simplicity, we will imagine that in the mathematical sense, in neural networks, neurons are understood as a certain container containing a number from zero to one.

Neuron activation. Neural network layers

Since our grid consists of 28x28=784 pixels, let there be 784 neurons containing different numbers from 0 to 1: the closer the pixel is to white, the closer the corresponding number is to one. These numbers filling the grid will be called activations of neurons. You can imagine this as if a neuron lights up like a light bulb when it contains a number close to 1 and goes out when a number is close to 0.

The described 784 neurons form the first layer of the neural network. The last layer contains 10 neurons, each corresponding to one of the ten digits. In these numbers, activation is also a number from zero to one, reflecting how confident the system is that the input image contains the corresponding digit.

There are also a couple of middle layers, called hidden layers, which we'll get to shortly. The choice of the number of hidden layers and the neurons they contain is arbitrary (we chose 2 layers of 16 neurons each), but usually they are chosen from certain ideas about the task being solved by the neural network.

The principle of the neural network is that the activation in one layer determines the activation in the next. Being excited, a certain group of neurons causes the excitation of another group. If we pass the trained neural network to the first layer the activation values according to the brightness of each pixel of the image, the chain of activations from one layer of the neural network to the next will lead to the preferential activation of one of the neurons of the last layer corresponding to the recognized digit - the choice of the neural network.

Purpose of hidden layers

Before delving into the mathematics of how one layer affects the next, how learning occurs, and how the neural network solves the problem of recognizing numbers, we will discuss why such a layered structure can act intelligently at all. What do intermediate layers do between input and output layers?

Figure Image Layer

In the process of digit recognition, we bring the various components together.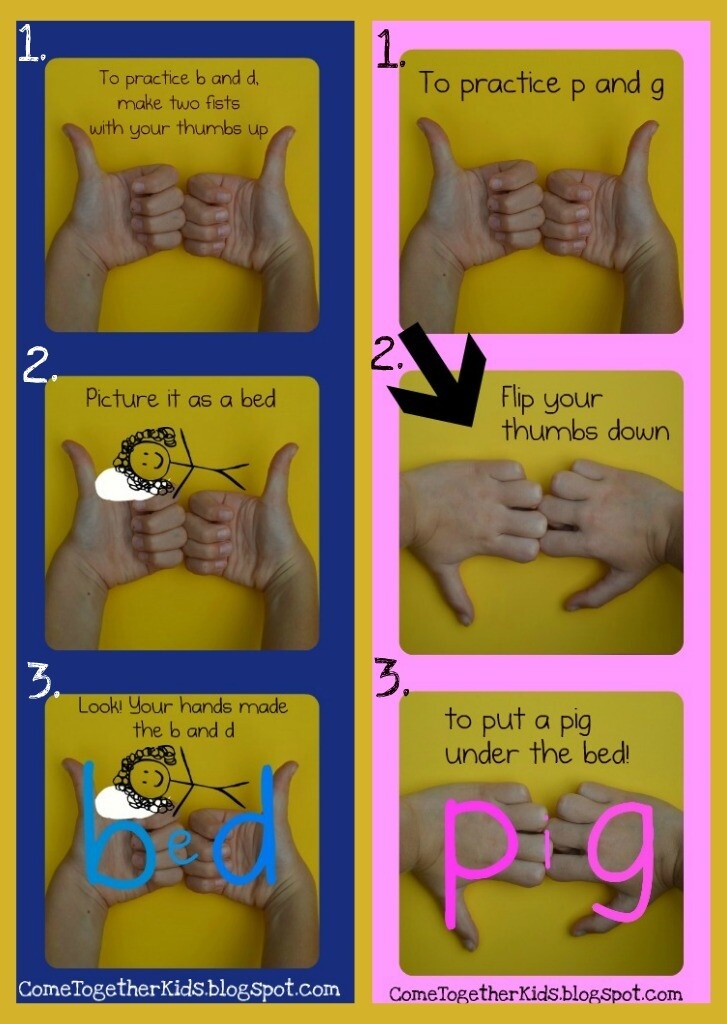 For example, a nine consists of a circle on top and a line on the right. The figure eight also has a circle at the top, but instead of a line on the right, it has a paired circle at the bottom. The four can be represented as three lines connected in a certain way. And so on.

In the idealized case, one would expect each neuron from the second layer to correspond to one of these components. And, for example, when you feed an image with a circle at the top to the neural network, there is a certain neuron whose activation will become closer to one. Thus, the transition from the second hidden layer to the output corresponds to the knowledge of which set of components corresponds to which digit.

Layer of images of structural units

The circle recognition task can also be divided into subtasks. For example, to recognize various small faces from which it is formed. Likewise, a long vertical line can be thought of as a pattern connecting several smaller pieces. Thus, it can be hoped that each neuron from the first hidden layer of the neural network performs the operation of recognizing these small edges.

Thus entered image leads to the activation of certain neurons of the first hidden layer, which determine the characteristic small pieces, these neurons in turn activate larger shapes, as a result, activating the neuron of the output layer associated with a certain number.

Whether or not the neural network will act this way is another matter that you will return to when discussing the network learning process. However, this can serve as a guide for us, a kind of goal of such a layered structure.

On the other hand, such a definition of edges and patterns is useful not only in the problem of digit recognition, but also in the problem of pattern detection in general.

And not only for recognition of numbers and images, but also for other intellectual tasks that can be divided into layers of abstraction. For example, for speech recognition, individual sounds, syllables, words, then phrases, more abstract thoughts, etc. are extracted from raw audio.

Determining the recognition area

To be specific, let's now imagine that the goal of a single neuron in the first hidden layer is to determine whether the picture contains a face in the area marked in the figure.

The first question is: what settings should the neural network have in order to be able to detect this pattern or any other pixel pattern.

Let's assign a numerical weight w _i to each connection between our neuron and the neuron from the input layer. Then we take all the activations from the first layer and calculate their weighted sum according to these weights.

Since the number of weights is the same as the number of activations, they can also be mapped to a similar grid. We will denote positive weights with green pixels, and negative weights with red pixels. The brightness of the pixel will correspond to the absolute value of the weight.

Now, if we set all weights to zero, except for the pixels that match our template, then the weighted sum is the sum of the activation values of the pixels in the region of interest.

If you want to determine if there is an edge, you can add red weight faces around the green weight rectangle, corresponding to negative weights. Then the weighted sum for this area will be maximum when the average pixels of the image in this area are brighter, and the surrounding pixels are darker.

Activation scaling to interval [0, 1]

By calculating such a weighted sum, you can get any number in a wide range of values. In order for it to fall within the required range of activations from 0 to 1, it is reasonable to use a function that would “compress” the entire range to the interval [0, 1].

The sigmoid logistic function is often used for this scaling. The greater the absolute value of the negative input number, the closer the sigmoid output value is to zero. The larger the value of the positive input number, the closer the value of the function is to one.

Thus, neuron activation is essentially a measure of how positive the corresponding weighted sum is. To prevent the neuron from firing at small positive numbers, you can add a negative number to the weighted sum - a bias, which determines how large the weighted sum should be in order to activate the neuron.

So far we've only talked about one neuron. Each neuron from the first hidden layer is connected to all 784 pixel neurons of the first layer. And each of these 784 compounds will have a weight associated with it. Also, each of the neurons in the first hidden layer has a shift associated with it, which is added to the weighted sum before this value is "compressed" by the sigmoid. Thus, for the first hidden layer, there are 784x16 weights and 16 shifts.

Connections between other layers also contain the weights and offsets associated with them. Thus, for the given example, about 13 thousand weights and shifts that determine the behavior of the neural network act as adjustable parameters.

To train a neural network to recognize numbers means to force the computer to find the correct values for all these numbers in such a way that it solves the problem. Imagine adjusting all those weights and manually shifting. This is one of the most effective arguments to interpret the neural network as a black box - it is almost impossible to mentally track the joint behavior of all parameters.

Description of a neural network in terms of linear algebra

Let's discuss a compact way of mathematical representation of neural network connections. Combine all activations of the first layer into a column vector. We combine all the weights into a matrix, each row of which describes the connections between the neurons of one layer with a specific neuron of the next (in case of difficulty, see the linear algebra course we described). As a result of multiplying the matrix by the vector, we obtain a vector corresponding to the weighted sums of activations of the first layer. We add the matrix product with the shift vector and wrap the sigmoid function to scale the ranges of values. As a result, we get a column of corresponding activations.

Obviously, instead of columns and matrices, as is customary in linear algebra, one can use their short notation. This makes the corresponding code both simpler and faster, since the machine learning libraries are optimized for vector computing.

Neuronal activation clarification

It's time to refine the simplification we started with. Neurons correspond not just to numbers - activations, but to activation functions that take values from all neurons of the previous layer and calculate output values in the range from 0 to 1.

In fact, the entire neural network is one large learning-adjustable function with 13,000 parameters that takes 784 input values and gives the probability that the image corresponds to one of the ten digits intended for recognition. However, despite its complexity, this is just a function, and in a sense it is logical that it looks complicated, because if it were simpler, this function would not be able to solve the problem of recognizing digits.

As a supplement, let's discuss which activation functions are currently used to program neural networks.

Addition: a little about the activation functions. Comparison of the sigmoid and ReLU

Let's briefly touch on the topic of functions used to "compress" the interval of activation values. The sigmoid function is an example that emulates biological neurons and was used in early work on neural networks, but the simpler ReLU function is now more commonly used to facilitate neural network training.

The ReLU function corresponds to the biological analogy that neurons may or may not be active. If a certain threshold is passed, then the function is triggered, and if it is not passed, then the neuron simply remains inactive, with an activation equal to zero.

It turned out that for deep multilayer networks, the ReLU function works very well and it often makes no sense to use the more difficult sigmoid function to calculate.

The question arises: how does the network described in the first lesson find the appropriate weights and shifts only from the received data? This is what the second lesson is about.

In general, the algorithm is to show the neural network a set of training data representing pairs of images of handwritten numbers and their abstract mathematical representations.

In general terms

As a result of training, the neural network should correctly distinguish numbers from previously unrepresented test data. Accordingly, the ratio of the number of acts of correct recognition of digits to the number of elements of the test sample can be used as a test for training the neural network.

Where does training data come from? The problem under consideration is very common, and to solve it, a large MNIST database was created, consisting of 60 thousand labeled data and 10 thousand test images.

Cost function

Conceptually, the task of training a neural network is reduced to finding the minimum of a certain function - the cost function. Let's describe what it is.

As you remember, each neuron of the next layer is connected to the neuron of the previous layer, while the weights of these connections and the total shift determine its activation function. In order to start somewhere, we can initialize all these weights and shifts with random numbers.

Accordingly, at the initial moment, an untrained neural network in response to an image of a given number, for example, an image of a triple, the output layer gives a completely random answer.

To train the neural network, we will introduce a cost function, which will, as it were, tell the computer in the event of a similar result: “No, bad computer! The activation value must be zero for all neurons except for the one that is correct. ”

Set cost function for digit recognition

Mathematically, this function represents the sum of the squared differences between the actual activation values of the output layer and their ideal values. For example, in the case of a triple, the activation must be zero for all neurons, except for the one corresponding to the triple, for which it is equal to one.

It turns out that for one image we can determine one current value of the cost function. If the neural network is trained, this value will be small, ideally tending to zero, and vice versa: the larger the value of the cost function, the worse the neural network is trained.

Thus, in order to subsequently determine how well the neural network was trained, it is necessary to determine the average value of the cost function for all images of the training set.

This is a rather difficult task. If our neural network has 784 pixels at the input, 10 values at the output and requires 13 thousand parameters to calculate them, then the cost function is a function of these 13 thousand parameters, it produces one single cost value that we want to minimize, and at the same time in the entire training set serves as parameters.

How to change all these weights and shifts so that the neural network is trained?

Gradient Descent

To start, instead of representing a function with 13k inputs, let's start with a function of one variable, C(w). As you probably remember from the course of mathematical analysis, in order to find the minimum of a function, you need to take the derivative.

However, the form of a function can be very complex, and one flexible strategy is to start at some arbitrary point and step down the value of the function. By repeating this procedure at each subsequent point, one can gradually come to a local minimum of the function, as does a ball rolling down a hill.

As shown in the figure above, a function can have many local minima, and which local minimum the algorithm ends up in depends on the choice of starting point, and there is no guarantee that the minimum found is the minimum possible value of the cost function. This must be kept in mind. In addition, in order not to "slip" the value of the local minimum, you need to change the step size in proportion to the slope of the function.

Slightly complicating this problem, instead of a function of one variable, you can represent a function of two variables with one output value. The corresponding function for finding the direction of the fastest descent is the negative gradient -∇С. The gradient is calculated, a step is taken in the direction of -∇С, the procedure is repeated until we are at the minimum.

The described idea is called gradient descent and can be applied to find the minimum of not only a function of two variables, but also 13 thousand, and any other number of variables. Imagine that all weights and shifts form one large column vector w. For this vector, you can calculate the same cost function gradient vector and move in the appropriate direction by adding the resulting vector to the w vector. And so repeat this procedure until the function С(w) comes to a minimum.

Gradient Descent Components

For our neural network, steps towards a lower cost function value will mean less and less random behavior of the neural network in response to training data. The algorithm for efficiently calculating this gradient is called backpropagation and will be discussed in detail in the next section.

For gradient descent, it is important that the output values of the cost function change smoothly. That is why activation values are not just binary values of 0 and 1, but represent real numbers and are in the interval between these values.

Each gradient component tells us two things. The sign of a component indicates the direction of change, and the absolute value indicates the effect of this component on the final result: some weights contribute more to the cost function than others.

Checking the assumption about the assignment of hidden layers

Let's discuss the question of how the layers of the neural network correspond to our expectations from the first lesson. If we visualize the weights of the neurons of the first hidden layer of the trained neural network, we will not see the expected figures that would correspond to the small constituent elements of the numbers. We will see much less clear patterns corresponding to how the neural network has minimized the cost function.

On the other hand, the question arises, what to expect if we pass an image of white noise to the neural network? It could be assumed that the neural network should not produce any specific number and the neurons of the output layer should not be activated or, if they are activated, then in a uniform way. Instead, the neural network will respond to a random image with a well-defined number.

Although the neural network performs digit recognition operations, it has no idea how they are written. In fact, such neural networks are a rather old technology developed in the 80s-90 years. However, it is very useful to understand how this type of neural network works before understanding modern options that can solve various interesting problems. But the more you dig into what the hidden layers of a neural network are doing, the less intelligent the neural network seems to be.

Learning on structured and random data

Consider an example of a modern neural network for recognizing various objects in the real world.

What happens if you shuffle the database so that the object names and images no longer match? Obviously, since the data is labeled randomly, the recognition accuracy on the test set will be useless. However, at the same time, on the training sample, you will receive recognition accuracy at the same level as if the data were labeled in the right way.

Millions of weights on this particular modern neural network will be fine-tuned to exactly match the data and its markers. Does the minimization of the cost function correspond to some image patterns, and does learning on randomly labeled data differ from training on incorrectly labeled data?

If you train a neural network for the recognition process on randomly labeled data, then training is very slow, the cost curve from the number of steps taken behaves almost linearly. If training takes place on structured data, the value of the cost function decreases in a much smaller number of iterations.

Backpropagation is a key neural network training algorithm. Let us first discuss in general terms what the method consists of.

Neuron activation control

Each step of the algorithm uses in theory all examples of the training set. Let us have an image of a 2 and we are at the very beginning of training: weights and shifts are set randomly, and some random pattern of output layer activations corresponds to the image.

We cannot directly change the activations of the final layer, but we can influence the weights and shifts to change the activation pattern of the output layer: decrease the activation values of all neurons except the corresponding 2, and increase the activation value of the required neuron. In this case, the increase and decrease is required the stronger, the farther the current value is from the desired one.

Neural network settings

Let's focus on one neuron, corresponding to the activation of neuron 2 on the output layer. As we remember, its value is the weighted sum of the activations of the neurons of the previous layer plus the shift, wrapped in a scaling function (sigmoid or ReLU).

So to increase the value of this activation, we can:

Increase the shift b.
Increase weights w _i .
Swap previous layer activations a _i .

From the weighted sum formula, it can be seen that the weights corresponding to connections with the most activated neurons make the greatest contribution to neuron activation. A strategy similar to biological neural networks is to increase the weights w _i in proportion to the activation value a _i of the corresponding neurons of the previous layer. It turns out that the most activated neurons are connected to the neuron that we only want to activate with the most "strong" connections.

Another close approach is to change the activations of neurons of the previous layer a _i in proportion to the weights w _i . We cannot change the activation of neurons, but we can change the corresponding weights and shifts and thus affect the activation of neurons.

Backpropagation

The penultimate layer of neurons can be considered similarly to the output layer. You collect information about how the activations of neurons in this layer would have to change in order for the activations of the output layer to change.

It is important to understand that all these actions occur not only with the neuron corresponding to the two, but also with all the neurons of the output layer, since each neuron of the current layer is connected to all the neurons of the previous one.

Having summed up all these necessary changes for the penultimate layer, you understand how the second layer from the end should change. Then, recursively, you repeat the same process to determine the weight and shift properties of all layers.

Classic Gradient Descent

As a result, the entire operation on one image leads to finding the necessary changes of 13 thousand weights and shifts. By repeating the operation on all examples of the training sample, you get the change values for each example, which you can then average for each parameter separately.

The result of this averaging is the negative gradient column vector of the cost function.

Stochastic Gradient Descent

Considering the entire training set to calculate a single step slows down the gradient descent process. So the following is usually done.

The data of the training sample are randomly mixed and divided into subgroups, for example, 100 labeled images. Next, the algorithm calculates the gradient descent step for one subgroup.

This is not exactly a true gradient for the cost function, which requires all the training data, but since the data is randomly selected, it gives a good approximation, and, importantly, allows you to significantly increase the speed of calculations.

If you build the learning curve of such a modernized gradient descent, it will not look like a steady, purposeful descent from a hill, but like a winding trajectory of a drunk, but taking faster steps and also coming to a function minimum.

This approach is called stochastic gradient descent.

Supplement. Backpropagation Math

Now let's look a little more formally at the mathematical background of the backpropagation algorithm.

Primitive neural network model

Let's start with an extremely simple neural network consisting of four layers, where each layer has only one neuron. Accordingly, the network has three weights and three shifts. Consider how sensitive the function is to these variables.

Let's start with the connection between the last two neurons. Let's denote the last layer L, the penultimate layer L-1, and the activations of the considered neurons lying in them a ^(L) , a ^(L-1) .

Cost function

Imagine that the desired activation value of the last neuron given to the training examples is y, equal to, for example, 0 or 1. Thus, the cost function is defined for this example as

C ₀ = (a ^{( L)} - y) ² .

Recall that the activation of this last neuron is given by the weighted sum, or rather the scaling function of the weighted sum: ^(L)).

For brevity, the weighted sum can be denoted by a letter with the appropriate index, for example z ^(L) :

a ^(L) = σ (z ^(L) ).

Consider how small changes in the weight w affect the value of the cost function ^(L) . Or in mathematical terms, what is the derivative of the cost function with respect to weight ∂C ₀ /∂w ^(L) ?

It can be seen that the change in C ₀ depends on the change in a ^(L) , which in turn depends on the change in z ^(L) , which depends on w ^(L) . According to the rule of taking similar derivatives, the desired value is determined by the product of the following partial derivatives:.

Definition of derivatives

Calculate the corresponding derivatives: and desired.

The average derivative in the chain is simply the derivative of the scaling function:

∂a ^(L) /∂z ^(L) = σ'(z ^(L) )

/∂w ^(L) = a ^(L-1)

Thus, the corresponding change is determined by how activated the previous neuron is. This is consistent with the idea mentioned above that a stronger connection is formed between neurons that light up together.

Final expression:

∂C ₀ /∂w ^(L) = 2(a ^(L) - y) σ'(z ^(L) ) a ^(L-1)

Backpropagation3

Recall that a certain derivative is only for the cost of a single example of a training sample C ₀ . For the cost function C, as we remember, it is necessary to average over all examples of the training sample: The resulting average value for a specific w ^(L) is one of the components of the cost function gradient. The consideration for shifts is identical to the above consideration for weights.

Having obtained the corresponding derivatives, we can continue the consideration for the previous layers.

Model with many neurons in the layer

However, how to make the transition from layers containing one neuron to the initially considered neural network. Everything will look the same, just an additional subscript will be added, reflecting the number of the neuron within the layer, and the weights will have double subscripts, for example, jk, reflecting the connection of neuron j from one layer L with another neuron k in layer L-1.

The final derivatives give the necessary components to determine the components of the ∇C gradient.

You can practice the described digit recognition task using the training repository on GitHub and the mentioned MNIST digit recognition dataset.

Writing your own neural network: a step-by-step guide
Neural Networks Toolkit
Illustrative video course in linear algebra: 11 lessons
Introduction to Deep Learning
Illustrative video course of mathematical analysis: 10 lessons
Beginner to Pro in Machine Learning in 3 Months

techniques and technologies of the multisensory approach

Multisensory learning is an approach that helps to perceive and transmit information by several senses simultaneously through different channels of perception.

"Multi" means plurality.

How it all began

In 1935, psychologists Samuel Orton and Anna Gingen defined the concept of multisensory learning. They pioneered the program to help struggling readers. They included multisensory exercises to teach the relationships between letters and sounds, the rules of phonetics. This structured approach helped students break down reading and spelling into small lessons and then improve step by step. So they mastered one skill before moving on to the next.

Multisensory activity involves several areas of the brain. To understand how multisensory learning works, it is important to understand how the mind works. The human brain has evolved to learn and grow in a multi-sensory environment. For this reason, all brain functions are interconnected. A person knows what to do best when instructions involve multiple senses. Many students rely on some senses more than others, so a variety of multi-sensory activities help children absorb the material.

Multisensory learning strategies are related to more established educational methods, such as Gardner's theory of multiple intelligences, which views intelligence under different conditions rather than as the dominance of one general ability. That is, each person has several types of intelligence, but usually three or four dominate.

Multisensory learning is a branch of student-centered learning, that is, the process of harmonious development of the personality, where the child feels himself a part of the process. Most often used at a younger age - early, preschool and in the beginning. Although the format is available for any age.

Research on multisensory learning

Cognitive psychologist Richard Mayer has investigated the complex effects of sensory stimuli on learning. He divided the participants into three groups: the first received information visually, the second heard, and the third used both methods. The latter memorized and reproduced information in more detail than the rest.

Head of the School of Advanced Studies at the Institute of Philosophy, University of London Barry Smith argues that the senses work together, and this is multisensory. That is, for example, we feel smells in two ways - externally, when we inhale the aroma of a bun, and internally, when we understand when we exhale whether it is worth eating. Another example: when we hear a sound, we use not only our ears, but also our eyes, which are looking for the source of this sound.

A 2018 study in cognitive science showed that children with the strongest literacy skills had more interaction between different areas of the brain. It was done using fMRI technology, which measures brain activity by detecting changes in blood flow.

How multisensory learning works

Depending on the leading channel of perception, children can be divided into auditory, visual, kinesthetic and discrete. When selecting educational materials, it is important to take into account the peculiarities of perception, and regularly changing tasks for different channels will help to adjust the attention of each child. Multisensory learning affects sensory and thus helps to concentrate and hold attention, activate imagination and thinking.

The multisensory approach is based on multisensory perception . This means that all or some combination of visual, auditory, gustatory, olfactory and tactile sensations can be involved at the same time. In another way, this system is called "I hear - I see - I feel." There can be any number of such combinations and in any order. In general, they can be used in any lesson.

Examples

In elementary school

Variant “I see - I hear - I speak” . This means that the child sees the bird, hears what sound it makes, and names it. Or a larger example: "I see - I feel with my nose - I hear with my ear - I touch" . The student sees an orange, inhales its smell, listens to see if there are any sounds in it, and studies with his hands.

This approach can be used not only during some activity, but also in the classroom. For example, when pets are studied in English. Children have plasticine, from which everyone sculpts their beast, pronouncing individual parts of the body. And then the guys exchange animals, pronouncing their names. Scheme 9 works here0383 "I do - I say - I see - I see - I say" .

In high school

An example of the scheme: "I see - I hear - I do" , when a teenager sees a chemical phenomenon - the burning of spirits, hears what sound comes from the burner and the flame itself, does it according to the model.

At the geometry lesson, you can analyze the topic "Prism" according to the scheme "I see - I do" . First, high school students see a sample on an interactive whiteboard, then use a wire to create a volumetric prism.

And in Literature, the whole class can read “War and Peace” aloud to engage the auditory and visual senses, that is, use the “hear-see” scheme.

Even small activities that involve multiple senses can teach students to use their entire brain.

For children with disabilities

Multisensory is often used to teach children with disabilities (HIA). For example, if a child has dyslexia, that is, difficulties in understanding letters and sounds, he can be offered to learn the alphabet with plasticine - to sculpt each letter. This is scheme "I see - I do - I say" . Literacy is a multi-sensory skill, as reading involves both recognizing written words and translating them into the appropriate letters.

For homeschoolers

If a child is at a distance of a thousand kilometers from a teacher, then he will be able to use some of the schemes if he prepares himself. For example, if you need smells or tactile sensations. And if it is a sound, picture or video, then the teacher will be able to take it upon himself.

For example, to understand the work of Sergei Dovlatov, the teacher will find his image, letters, voice recordings, if they have survived. The child will be able to use the See-Hear-Speak Chart to discuss works and biography.

Instructional strategies for teaching letter recognition

Tips and Activities for Teaching Alphabet Recognition

Alphabet Matching | Classroom Strategies

More phonics strategies

Why teach about the alphabet?

Watch: Alphabet In My Mouth!

Collect resources

Matching upper-case and lower-case

Letter formation: using sand, play dough, or flour

Letter bingo

Letter stamps

Letter recognition fluency

Letter books

Downloadable letter and alphabet cards

Flash cards

Alphabet cards

Race track alphabet

Differentiated instruction

for Second Language Learners, students of varying reading skill, and for younger learners

See the research that supports this strategy

Children's books to use with this strategy

Farm Alphabet Book

Kipper's A to Z: An Alphabet Adventure

Eating the Alphabet

Chicka Chicka Boom Boom

ABC: A Child's First Alphabet

Comments

A visual introduction to neural networks using the example of digit recognition

Number Recognition Problem Statement

Neuron activation. Neural network layers

Purpose of hidden layers

Figure Image Layer

Layer of images of structural units

Determining the recognition area

Activation scaling to interval [0, 1]

Description of a neural network in terms of linear algebra

Neuronal activation clarification

Addition: a little about the activation functions. Comparison of the sigmoid and ReLU

In general terms

Cost function

Set cost function for digit recognition

Gradient Descent

Gradient Descent Components

Checking the assumption about the assignment of hidden layers

Learning on structured and random data

Neuron activation control

Neural network settings

Backpropagation

Classic Gradient Descent

Stochastic Gradient Descent

Supplement. Backpropagation Math

Primitive neural network model

Cost function

Definition of derivatives

Backpropagation3

Model with many neurons in the layer

techniques and technologies of the multisensory approach

How it all began

Research on multisensory learning

How multisensory learning works

Examples

In elementary school

In high school

Even small activities that involve multiple senses can teach students to use their entire brain.

For children with disabilities

For homeschoolers

Learn more