Home » Misc » Math concepts by grade

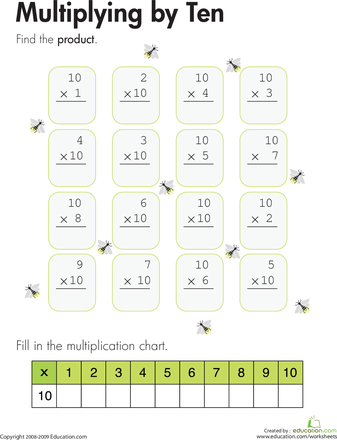
Math concepts by grade


Math Skills by Grade Level

Unless you are a teacher, or you hyper-analyze every math assignment your child gets, it can be hard to know exactly what they should be mastering at each grade level. Is it appropriate to ask your Kindergartener to count the change you got from the supermarket? Can you depend on your 5th grader to accurately convert measurements for a recipe? You probably know the answer because you know your kids! But what should they know and be able to do?

The exact skills expected at each grade level depend on where you live and the kind of school your children attend. But whether their school follows Common Core, Next Gen, or some other framework for learning standards, there are some basic milestones that your child should be meeting based on her developmental age. Here’s what you should expect your child to be able to do as she progresses through the grades. Keep in mind that the skills listed below each grade are what she should be expected to do by the end of the year!

Kindergarten

This is where students learn basic number sense. Counting, one-to-one correspondence (being able to recognize the specific quantity in a set of objects), and addition and subtraction within 10 are the major skills your kindergartener will be working on. Students will also begin to describe shapes using informal vocabulary like “curve,” “flat,” “corner,” “edge,” etc.

First Grade

Students now learn various addition and subtraction strategies and can solve addition and subtraction problems within 20. They should be able to count to or above 100 and begin comparing measurements of objects. They should also be able to tell time on an analog clock to the hour and half hour.

Second Grade

By the end of second grade, students should be able to skip count by fives, tens, and hundreds. This forms the basis for next year’s introduction to multiplication. They should be fluent with adding and subtracting within 100 and should be able to apply strategies they’ve learned to problem solve within 1,000. Their measurements become more accurate and they begin to estimate.

Third Grade

In third grade, students begin learning about multiplication, division, and fractions. They explore and should eventually understand the relationship between multiplication and division, and they begin to relate their knowledge of both to fraction concepts. They are also introduced to area and perimeter of rectangles.

Fourth Grade

Students in Grade 4 become fluent with all four operations and should be able to use a variety of strategies in problem solving with multi-digit numbers. They start exploring division with remainders. They should be able to create and analyze mathematical patterns and will learn the terms ‘factor’ and ‘multiple.’ They are also introduced to decimals as they relate to fractions and begin converting measurements.

Fifth Grade

Students begin writing their own mathematical expressions to represent situations, both real and imagined. They can solve multi-digit problems in all four operations involving decimals and fractions. They are introduced to volume of objects, the coordinate plane, and properties of angles.

Sixth Grade

In addition to full mastery of skills in all previous grades, students are introduced to the following new concepts: ratios and proportions, statistics, rational and irrational numbers, inequalities, dependent and independent variables, and pre-algebra concepts.

Seventh Grade

Students in seventh grade apply the four operations to rational numbers. They can analyze proportional relationships in the real world and can solve problems involving angles, area, surface area and volume. They should also be able to interpret different types of data sets in order to make inferences.

Eighth Grade

By the end of eighth grade, students should be able to work with linear equations and functions, and they should know how to solve problems with radicals and exponents. This year, students learn the Pythagorean Theorem and should be able to apply it. They should also be able to find the volume and surface area of spheres, cones, and cylinders.

High School

Math skills in high school are no longer separated by grade level, but by topic. By the end of high school, students should be able to demonstrate the following skills:

Numbers/Quantities

  • Fluency with exponents and rational/irrational numbers

  • Understanding of imaginary numbers

  • Understand and use vectors and matrices

Algebra

  • Solve polynomials

  • Rewrite rational functions

  • Solve systems of equations

  • Solve and graph equations and inequalities

Functions

  • Understand functions and use function notation

  • Build and re-construct functions

  • Build and compare linear and exponential models

  • Understand basic trigonometry

Geometry

  • Understand transformations and congruence

  • Prove theorems, including with the use of coordinates

  • Explain formulas and use them to solve problems

Statistics and Probability

  • Summarize, represent, and interpret data and linear models

  • Calculate probability in a variety of situations

  • Evaluate experiments, surveys, and studies

  • Understand independence and conditional probability

Conclusion

This year has made it very challenging to keep up with demanding curricula. It’s possible that your students have not yet been introduced to a topic listed above. That’s okay! Trust their current and future teachers to be able to help address the gaps along the way, but you can also reach out to one of our amazing educators for additional tutoring support. Confidence in math can be a delicate thing, and our certified educators and math tutors are pros when it comes to boosting it!

The 4 Major Math Concepts Your Kids Learn in Grades 1-2

So many fun and important ideas are being introduced in first and second grade! I love when I get to work with this age group because they get excited trying new things and are open to new ways of learning. Below are some of the major concepts taught in first and second grade math, as well as tips on how you can support your child(ren) at home.

1. Addition & Subtraction. 1st and 2nd graders extend their previous understanding from kindergarten with adding and subtracting. They begin to memorize their addition and subtraction facts up to 20, as well as solve word problems using objects, drawings, and equations. Children also begin to solve problems with more than two numbers and determine if a number is even or odd.

Encourage your child to:

  • Create and draw stories about adding and subtracting. For example:
     
     Addition    : Some bunnies were sitting on the grass. Three more bunnies hopped over to sit with them. Then there were five bunnies. How many bunnies were on the grass before? ? + 3 = 5
    Subtraction: Five apples were on the table. I ate some apples. Then only three apples were left. How many apples did I eat? 5 – ? = 3
  • Practice their addition and subtraction facts by playing games with numbers, dice, online, etc.
  • Decide if numbers they see in the real world are even or odd.

2. Number Sense. Your 1st and 2nd grader is also beginning to understand the concept of place value. Your child is learning about each place — ones, tens, and hundreds — by drawing pictures, counting in groups, and using base ten blocks. They are writing numbers up to 1,000 and comparing numbers. They are also building their mental math skills by solving problems mentally.

Encourage your child to:

  • Read numbers out loud and record numbers you say verbally.
  • Practice understating place value by deciding what the value of a digit is in a specific number.  For example: How much is the digit 7 worth in the number 379? 70 because the 7 is in the tens place.
  • Compare numbers using symbols: > (greater than), < (less than), or = (equal to). Play a game where you give them two numbers: 14 and 40. They can answer 14 < 40. Or 40 is > 14.
  • Solve problems mentally. For example: What is 75 + 20? 95

3. Measurement & Data. 1st and 2nd graders are beginning to understand measurement by estimating and measuring using rulers to the nearest inch, foot, yard, etc. They are beginning to count and use money to solve problems. Children are also figuring out how to tell time using both analog and digital clocks, as well as describing and creating different graphs.

Encourage your child to:

  • Estimate how long they think different objects are around the house and use rulers or tape measures to determine the actual size.
  • Read different looking clocks and use appropriate language describing the time using a.m. and p.m.
  • Collect and organize different data.
  • Find graphs in newspapers, magazines, online and compare them.

4. Geometry. In 1st and 2nd grade, children extend their previous understanding from kindergarten with 2-D and 3-D shapes. They examine the attributes of these shapes and are looking at the number of sides, angles, faces, etc. Children also beginning to partition shapes into equal pieces and use appropriate language.

Encourage your child to:

  • Identify 2-D shapes in the world: triangles, quadrilaterals, pentagons, hexagons, and octagons.
  • Identify 3-D shapes in the world: cubes, cones, cylinders, spheres, and triangular and rectangular prisms.
  • Count and find the number of sides or faces and angles each shape has.
  • Cut (partition) circles and rectangles into equal size pieces and use language such as halves, thirds, half of, a third of, etc.

Featured Photo Credit: Ableimages/Thinkstock

Have questions about your child’s math? Submit them to Jennifer here so she can consider answering in an upcoming blog. Or Share them with us on the Scholastic Parents Facebook Page.

Formation of mathematical concepts in primary school

Author: Grebennikova Anna Andreevna

Formation of mathematical concepts in primary school

Annotation: The article discusses various ideas on the formation of scientific concepts and their influence on modern ideas about the formation of the concept of number in younger students.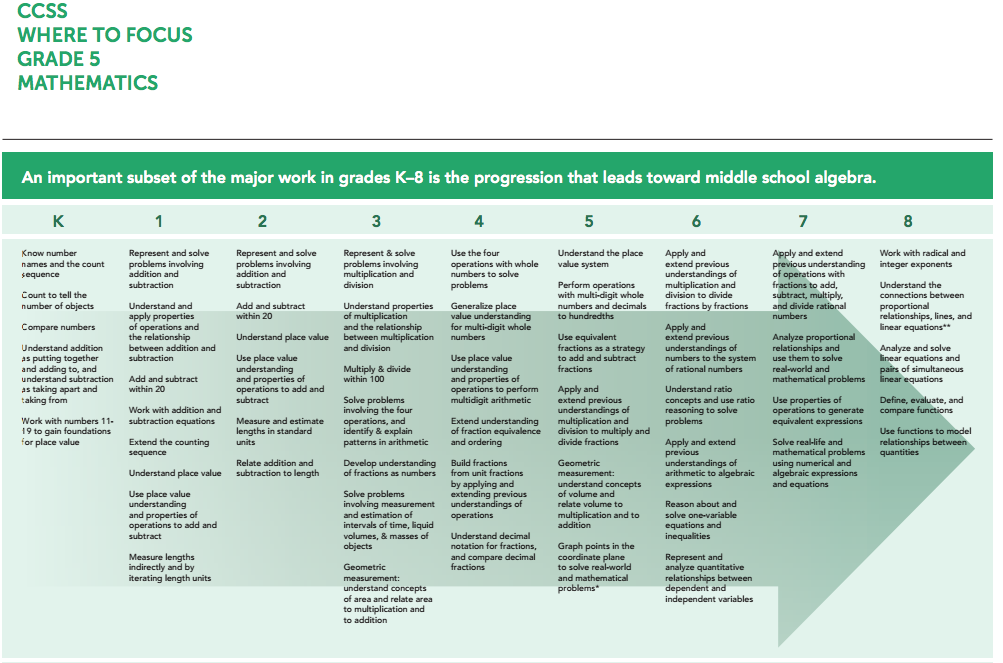

Key words: concept, number concept, generalization, various methodological approaches.

When acquiring scientific knowledge, elementary school students encounter different kinds of concepts. The student's inability to differentiate concepts leads to their inadequate assimilation.

Logic in concepts distinguishes scope and content. The volume is understood as the class of objects that belong to this concept, are united by it. So, the scope of the concept of a triangle includes the entire set of triangles, regardless of their specific characteristics (types of angles, size of sides, etc.).

The content of the concepts includes that system of important properties, due to which the process of uniting these objects into one class takes place. In order to reveal the essence of a concept, it is necessary, by means of comparison, to identify what signs will be sufficient to highlight its relationship to other objects. Until the moment when the signs are established, as well as the content, we will not be clear about the essence of the subject that is reflected by this concept.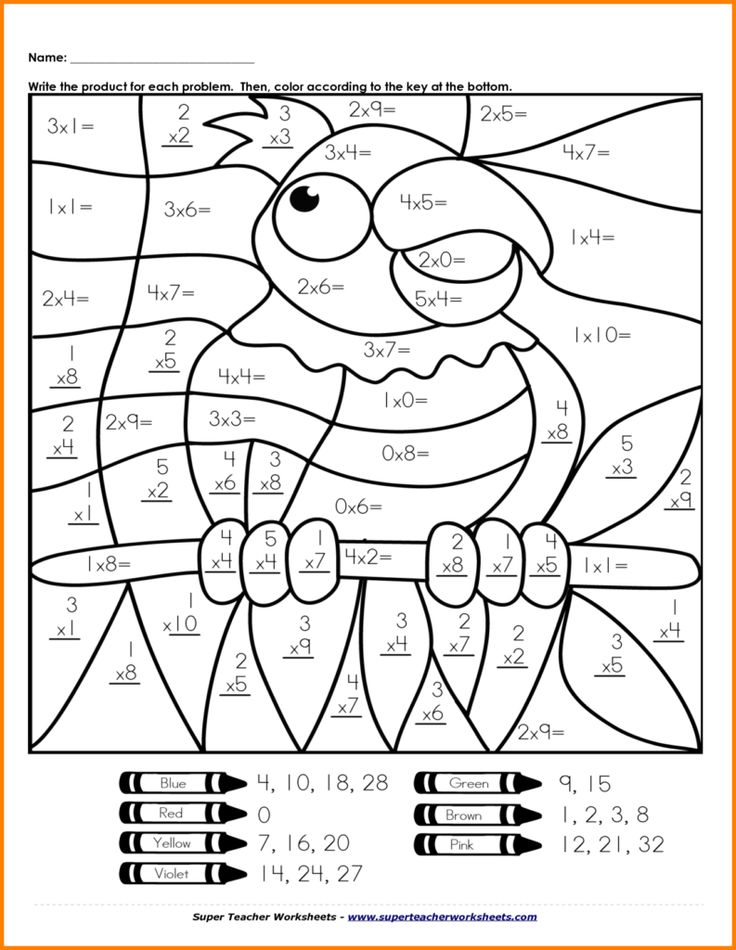 It will definitely be very difficult to separate such an object from adjacent objects, there will be some confusion.

If, for example, we talk about the concept of a triangle, then the properties can be attributed to such as a closed figure, consisting of three straight line segments. The set of properties, according to which objects are combined into one class, is usually called sufficient features or necessary features. In some concepts, these features can complement each other, thereby forming a content that allows you to combine objects into one class. An example of such concepts is a triangle, an angle, a bisector, and many others.

The set of such objects to which this concept will apply is a logical class of objects, which, in turn, is a collection of objects that have common features, and therefore are defined by a common concept. Concepts can be divided into types according to content, volume. It all depends on the nature and number of objects to which they are distributed. If we take the scope of a concept as a criterion, then it should be said here that concepts are divided into general and singular. For example, if the scope of a concept includes one object, then such a concept is called a single one. If we talk about the content, then the concepts can be divided into conjunctive and disjunctive, absolute and concrete, irrelative and relative. Conjunctive should be understood as such concepts that are interconnected by their features, that is, it is not possible to recognize an object of this class by individual features. For example, objects related to the concept of a triangle must necessarily consist of three line segments and be closed.

In other concepts, the relationship between necessary and sufficient features is different: they do not complement each other, but replace. This means that one feature is equivalent to the other. Such a connection of attributes is called disjunction, and the concepts are respectively called disjunctive. It is also important to take into account the division of concepts into absolute and relative.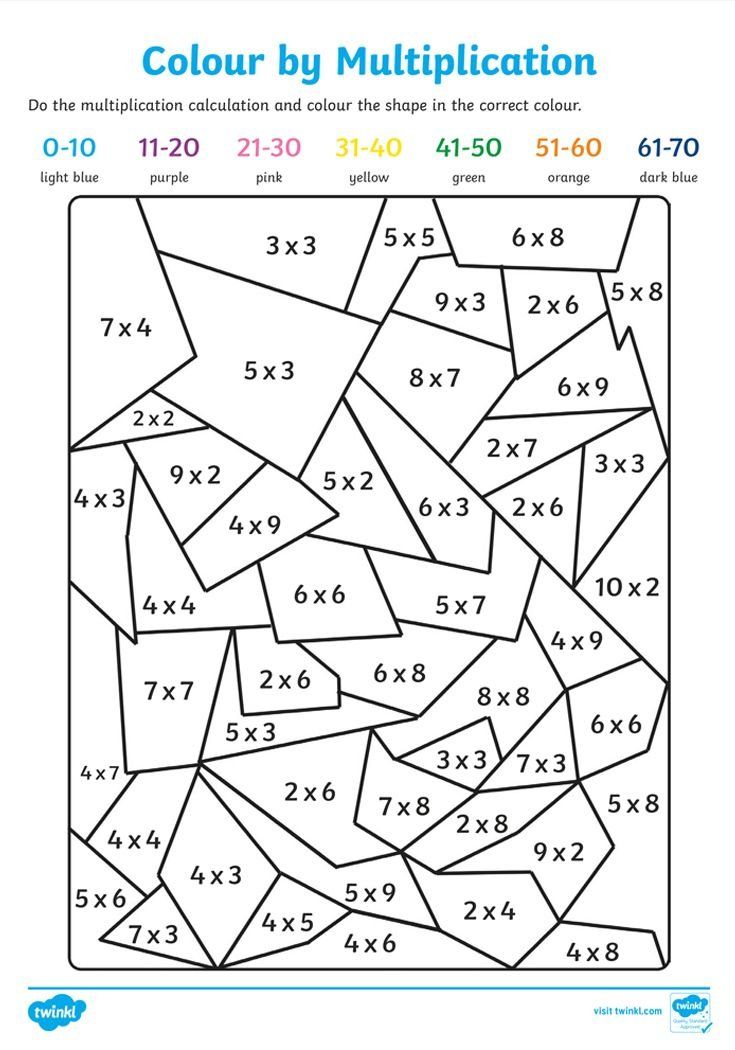 Absolute concepts can unite objects into classes, according to some features that characterize the essence of these objects. Relative concepts, on the other hand, set themselves the task of uniting them into classes according to properties that characterize their relationship to other objects.

Relative concepts cause more serious difficulties for students than absolute concepts. The essence of the difficulties lies precisely in the fact that schoolchildren do not take into account the relativity of concepts and operate with them as with absolute concepts.

In elementary school, each concept is initially introduced through visualization, through observation of specific objects, or through practical operation. In this case, the teacher is trying to build on the knowledge and experience of the children that they received early, perhaps even at preschool age. The teacher fixes acquaintance with the concepts of mathematics with the help of terms or symbols. But this does not mean that various types of definitions are not used at this stage of the work. The definition of a concept is a listing of all the important features of objects that are components of this concept. The definition of a concept by a word will be called a term, for example, “circle”, triangle. The tasks of the definition are very important: to single out and separate a certain concept from all the others, to indicate those essential features without which this concept cannot exist, on which all other features will depend. In the process of teaching children in elementary school, contextual and ostensive definitions are of particular interest among implicit definitions.

Any passage from the text, whatever the context, in which the concept that interests us occurs, is, in a sense, an implicit definition of it. Context allows you to put the concept in connection with other concepts, revealing their content.

For example, when working with children such expressions as “find the values ​​of the expression”, “compare the value of the expressions 5 + a and (a - 3) 2, if a = 7”, “read expressions that are sums”, “ read expressions, and then read equations”, we reveal the concept of “mathematical expression” as a record that consists of numbers or variables and signs of actions. It should be noted that almost all definitions that we encounter in life will be contextual definitions, since if we hear an unfamiliar word, we try to figure out its meaning ourselves, based on the general meaning of what was said. Such a phenomenon is present in the system of teaching younger students, since some mathematical concepts are defined in elementary school through the context.

These are, for example, such concepts as “big - small”, “any”, “any”, “one”, “many”, etc.

Contextual definitions remain largely incomplete and incomplete. They are used in connection with the unpreparedness of the younger student to assimilate the full and, all the more so, the scientific definition.

Ostensive definitions are definitions by demonstration. They resemble ordinary contextual definitions, but the context here is not a passage of some text, but the situation in which the object denoted by the concept finds itself. For example, the teacher shows a square (drawing or paper model) and says "Look - it's a square. " This is a typical ostensive definition.

In elementary grades, ostensive definitions are used when considering such concepts as “red (white, black, etc.) color”, “left - right”, “left to right”, “number”, “preceding and following number”, "signs of arithmetic operations", "comparison signs", "triangle", "quadrilateral", "cube", etc.

Thanks to the assimilation of the meanings of words in an ostensive way, it is possible to introduce into the child's vocabulary the already verbal meaning of new, previously unfamiliar words, as well as entire phrases. It is ostensive definitions that can connect a concept with objects. In elementary school, there are usually some acceptable definitions, like "We'll use the word 'pentagon' to mean a polygon with five sides." This, one might say, would be a nominal definition. Various explicit definitions are used in mathematics. The most common of them is the definition through the nearest genus and species character. The generic definition is also called the classical one.

Examples of definitions in terms of genus and species: “A parallelogram is a quadrilateral whose opposite sides are parallel”, “A rhombus is a parallelogram whose sides are equal”, “A rectangle is a parallelogram whose angles are right”, “A square is a rectangle, in which the sides are equal”, “A square is a rhombus with right angles”.

Let's analyze such concept as a square. Speaking about the first definition, it should be said about the nearest generic concept - "rectangle", where the species attribute will be - "all sides are equal." In the second definition, the closest genus is "rhombus", and the specific feature is "right angles". And if we take a genus that will not be the closest, then there will be two specific signs of a square, for example: "A parallelogram is called a square, in which all sides are equal and all angles are right." Some definitions allow us to consider concepts according to the method of its formation, as well as according to the method of its occurrence. Such definitions are usually called genetic

Examples of genetic definitions: "Angle is the rays that come out from one point", "The diagonal of a rectangle is a segment that connects the opposite vertices of the rectangle." In elementary grades, genetic definitions are used for such concepts as "segment", "broken line", "right angle", "circle".

Thus, it is quite clear that at primary school age there are a lot of concepts of mathematics that are initially assimilated superficially, that is, at first, schoolchildren get acquainted only with some properties of concepts, which does not allow them to fully understand their scope. This, in our opinion, is a natural stage, since not all concepts are easily assimilated. But the fact is that the understanding and timely use by the teacher of various types of definitions of mathematical concepts is a condition for the formation in children of stable knowledge about such concepts.

References:

1. Bogdanovich M.V. Definition of mathematical concepts // Primary school 2011. - No. 4.

2. Gluzman NA Formation of generalized methods of mental activity in younger schoolchildren. - Yalta: KSGI, 2012. - 34 p.

3. Drozd V.L. Urban M.A. From small problems to big discoveries. //Primary School. - 2010. - № 5.

Mathematical concepts | Educational and methodical material on mathematics on the topic:

Slide 1

Methods of mathematics Primary school teacher: Anikina Tatyana Yurievna

Slide 2

Mathematical concepts Concepts, their scope and content. The relationship of genus and species between concepts. Explicit and implicit definitions of concepts. Algorithm for solving the problem of recognition using the definition through the genus and specific difference. Examples of explicit and implicit definitions of concepts.

Slide 3

Concepts, their scope and content Concepts related to numbers and operations on them: number; addition; term; more. Algebraic concepts: expression; the equation; equality. Geometric concepts: segment; straight; triangle. Quantities and their measurement: centimeter; meter; kilometer.

Slide 4

The scope of a concept is the set of all objects denoted by one term. is the set of all essential properties of the object reflected in this concept. The content of the concept

Slide 5

Interrelation The scope of the concept The content of the concept

Slide 6

Relationships of genus and species between concepts Relationships between concepts are closely related to the relationships between their volumes, i.e. sets. ! If A with B (A=/ B), then a is specific in relation to the concept b, and the concept b is generic in relation to the concept a. If A = B, then the concepts a and b are identical. If the sets A and B are not connected by an inclusion relation, the concepts a and b are not in relation to the genus and species and are not identical.

Slide 7

Properties: 1) The concepts of genus and species are relative. 2) For a given concept, it is often possible to specify several generic concepts. 3) A species concept has all the properties of a generic concept. and implicit definitions of concepts Defined concept Generic concept Specific difference Defining concept + A definition is usually a sentence that explains the essence of a new term (or designation). !

Slide 10

Remember!!! 3. The definition should be clear 2. There should be no vicious circle in the definition (or their system) 4. The same concept can be defined in different ways. 1. The definition must be proportionate

Slide 11

Algorithm: Name the concept (term) being defined. 2. Indicate the closest generic (in relation to the defined) concept. 3. List the properties that distinguish the defined objects from the scope of the generic, i.e. state the difference. 4. Check whether the rules for defining the concept are met (is it proportionate, is there a vicious circle, etc.)

Slide 12

Explicit definitions Have the form of equality, coincidence of two concepts. The general scheme of such definitions is: "A is (by definition) B". Here A and B are two concepts, and it does not matter whether each of them is expressed by one word or a combination of words. Geometry is the science of the properties of geometric shapes. A molecule is the smallest particle of a substance that retains all the chemical properties of this substance. This definition is by display. They are used to introduce terms, by demonstrating the objects that these terms designate.

Slide 14

X + 6 = 15 is an equation An example of a contextual definition can be the definition of an equation and its solution given in a mathematics textbook for grade II (Moro M.I., Bantova M.A. Mathematics: Textbook for 2 class of a four-year elementary school.) Here, after writing + 6 \u003d 15 and a list of numbers 0,5,9,10, there is a text: “To what number must 6 be added to get 15? We denote the unknown number with the Latin letter X (x): To solve an equation means to find an unknown number. In this equation, the unknown number is 9, since 9+6=15. "Explain why the numbers 0.5 and 10 are not appropriate."

Slide 15

2*7 >2*6 is inequality 17-5=8+4 is equality inequalities) from other sentences, it does not indicate the properties characteristic of these concepts. They only associate terms with the objects they define.

Slide 16

Geometric shapes Definition of a segment, ray, angle, polyline. The main properties of these figures. The content of these concepts in elementary education in mathematics; types of definitions. Task examples.

Slide 17

Definition of a segment, ray, angle, polyline A segment is a straight line passing through two points. is a system of two points A and B belonging to the line a. The points located between A and B are called the points lying inside the segment AB, the points A and B are called the ends of the segment AB. - A B is a part of a straight line, which consists of all points of this straight line lying between two given points of it. These points are called the ends of the segment.

Slide 18

Main property: Of the three points on a line, one and only one lies between the other two. Two points are enough to draw a straight line.

Slide 19

A ray is a part of a straight line that has a beginning but no end. - The beam is limited on one side and can be extended in a straight line only in one direction, as far as desired. - A ray with origin O is a set of all points of a straight line lying on one side of O.

Slide 20

О A ray is a part of a straight line, which consists of all points of this straight line, lying on one side of its given point. This point is called the starting point of the beam.

Slide 21

An angle is a figure formed by two rays with the same origin. A B The rays forming an angle are called the sides of the angle, and their common beginning is the apex of the angle. An acute angle is an angle that is less than a right angle. An obtuse angle is an angle that is greater than a right angle. A right angle equal to 90 is a set of two rays with a common origin, lying on different lines. - - From

Slide 22

Basic properties: Each angle has a certain degree measure greater than zero. A straight angle is 180. The degree measure of an angle is equal to the sum of the degree measures of the angles into which it is divided by any ray passing between its sides.

Slide 23

Polyline - B A C D E Polyline ABCDEG . Points A, B, C, D, E, G are the vertices of the polyline. The segments AB, BC, CD, DE, EG are the links of the broken line. G is a figure that consists of points A1, A2,……A n and segments A1A2, A2A3,…..A n A n connecting them.

Slide 24

Main property: The length of the polyline is not less than the length of the segment connecting its ends. The length of a broken line is the sum of the lengths of its links.

Slide 25

Sample tasks What is the broken line that has the most links? Less links? Which polyline has 3 vertices? 4 peaks? How to find out which segment is larger?

Slide 26

How can you draw a right angle on unlined paper? How to make 4 right angles with just two segments? And now 2 sharp and 2 blunt?

Slide 27

Rectangle A quadrilateral with all right angles.

Learn more