Home » Misc » Math concepts for preschool

Math concepts for preschool


The 4 Major Math Concepts Your Kids Learn in PreK & Kindergarten

There are so many different topics our children learn throughout the year, just keeping up with each night’s new piece of homework and its latest ideas can feel very overwhelming. As parents, we don’t get to see the major idea behind the “everyday” work and it can be frustrating to understand where each skill is going. In this first blog post of a continuing series, I will be highlighting the major math concepts that are taught at the different grade levels so we, as parents, can help to build and support these ideas at home.

Here are the four major math concepts taught in pre-kindergarten and kindergarten, along with exercises you can practice with your children to help reinforce their learning.

1. Counting. Students are beginning their experience with numbers through counting, number names and written numerals. Students are learning to count objects and understand a one-to-one correspondence. They are also starting to compare different sets of objects and use appropriate language.

Encourage your child to:

  • Touch different objects and count out loud.
  • Move objects from one group to another.
  • Count a set of objects and “see” or “write” that corresponding number.
  • Start to use comparing words: more than, less than, the same as.

2. Addition & Subtraction. This is the very early stage of adding and subtracting. The focus should be on developing an understanding of addition as “putting together and adding to,” and subtracting as “taking apart and taking from.” Students do not need to write equations at this young an age, but are encouraged to begin using them.

Encourage your child to:

  • Tell stories about adding and subtracting. For example, for addition: Two bunnies sat on the grass. Three more bunnies hopped there. How many bunnies are on the grass now? For subtraction: Five apples were on the table. I ate two apples. How many apples are on the table now? Draw pictures about putting together and taking apart.
  • Count to 10 and break apart numbers (decompose – math’s fancy word for “breaking apart”) into different combinations. For example, 5 can be seen as:

Image Credit: http://kindercraze.com

3. Measurement & Data. Young children are beginning to describe and compare their physical world. They are starting to classify, sort and group objects into categories.

Encourage your children to:

  • Compare two different objects using appropriate language. For example:
    “John is taller than Sarah.”
    “This tree is shorter than that tree.”
    “My bag is heavier than your bag.”
  • Sort objects by color, size, material, etc.
  • Describe their physical world with directional words: in front of, behind, on top of, next to, below, etc.

4. Geometry. Students are starting to look at and compare two-dimensional (flat) and three-dimensional (solid) shapes. They are using appropriate language to recognize different shapes and talk about their attributes.

Encourage your child to:

  • Find 2-D shapes in the world: squares, circles, triangles, rectangles, and hexagons.
  • Find 3-D shapes in the world: cubes, cones, cylinders, and spheres.
  • Count the different number of sides, vertices, angles, etc.Model different shapes using clay, sticks, pipe-cleaners, etc.

See all blog posts in this series for information on what your child will learn in math class from preschool all the up through 8th grade. 

The Most Important Math Concepts Kids Learn in Pre-K

Although there’s a lot of emphasis placed on emergent reading, experts show that pre-k math skills are just as important for your child’s learning development.

Understanding what skills your child will be exposed to as a math beginner will give you an idea of what concepts you can emphasize in fun, easy ways at home!

Fortunately, kids are exposed to many math concepts from a very young age — putting puzzles together, sorting objects, and even playing with building blocks. These activities all help build a good foundation for math.

In this article, we’ll take you through the most important pre-k math concepts so you can encourage and motivate your budding mathematician!

Table Of Contents

  • What Are The Components Of Pre-K Math?
  • Basic Pre-K Math Checklist
  • Pre-K Math Development
  • 9 Fun Pre-K Math Activities

What Are The Components Of Pre-K Math?

There are five basic components of pre-k math. They act like umbrella terms, each with many different elements hidden inside their broad concepts.

Your child will become acquainted with all of these essential concepts when they begin learning pre-k math.

1) Numbers And Counting

Children typically start with the bedrock of math — numbers! They’ll learn number names and how to write numbers, typically beginning with 1-10.

Counting is not easy business! While your child learns how to count — first with physical objects, then conceptually — they are bound to make mistakes here and there. This is perfectly all right. Counting will take time to master.

Most of kids’ initial exposure will be through representational counting. This could mean counting the number of strawberries in their lunch box, how many blocks are on the floor, and so on. These counting activities will set the stage for a strong foundation in counting.

By understanding that numbers represent objects, your child will begin to understand one-to-one correspondence (each object counted gets its own number and only that number) as well as the counting principle that when counting the number of objects, the last number counted equals the amount present.

Over time, a child’s reliance on physical objects for counting will decrease. They’ll depend more on conceptual counting as their skills develop.

This conceptual counting is called “number sense.” They’ll understand that quantities, whether tangible or theoretical, are countable. They’ll also learn that numbers can be compared: two or more numbers can have a more-than, less-than, or same-as number relationship.

There are many fun ways to get your child comfortable with numbers and counting at home without making it feel burdensome.

Here are a few simple yet effective strategies you can try:

  • Encourage your child to touch and count objects they see in everyday life — for example, a bunch of bananas or a stack of books.
  • After they count a set of objects, help them write down the corresponding number on a piece of paper.
  • Have your child compare different items using the appropriate language. For example, “Let’s count the number of blueberries and strawberries on the plate. Are there more strawberries than blueberries?”
  • Hang a simple number line on the wall or tape one to your refrigerator. Throughout the day, point to each number with your child and count from 1-10 together.
  • Ask your child to help set the table by counting out the right number of forks and spoons. Once they have collected them, they can count them again as they put one at each place setting.

These simple activities allow children to make sense of numbers. And the more they practice counting principles outside of the classroom, the more they’ll realize how relevant they are to everyday life.

2) Addition And Subtraction

Once your child has a firm grasp on counting and is developing number sense, they’ll explore the relationships between numbers more often. Describing how numbers are the same or different will lead into learning how to combine two numbers to make a new number!

Similar to the last concept, children will typically learn how to add and subtract by relying on counting activities with tangible objects. For example, you could set up two separate groups of apples and ask how many you will have if you join them together.

The first group may have three apples, while the second group has two apples. At first, many children will count one group and then start over to count the second group. It is a good idea to count both groups individually and then bring them together and count the total amount.

This is their first introduction to addition! The same idea works for subtracting. What happens when you begin with five apples and then take away two of them?

“Taking away” objects may be a little harder for your child to master at first. This is why many children will remove apples first and then count the remaining apples rather than counting backward.

To help, practice counting backward together. Pretend to be a rocket ship, and start counting down from five to one, gradually increasing the beginning number each time. After you get to one, shout, “Blastoff!” and jump into the air as high as you can. This fun game can help your child become more comfortable with counting down.

Pictures can also help your child master addition and subtraction concepts. For addition practice, present one sheet of paper with three apples and another with two. Then say, “Count the apples on both pieces of paper. How many apples do you have total?”

For subtraction problems, present this scenario: “On our paper, we have five apples total. How many apples will you see if I cover up two of them?” Then, count the remaining apples together.

Pictures are an effective way for your child to visualize mathematical problems. But, if you prefer not to draw, you can also use real objects instead. You could get out several apples (stuffed animals, cups, or whatever) and count them. Then, use those items for math practice.

Remember that adding and subtracting are basically making comparisons between numbers or establishing relationships between them. There are many strategies a child might use to solve a problem, which is a good thing since our main goal is to help children think mathematically.

3) Geometry And Spatial Reasoning

Shapes are everywhere in our world, which will be one of your greatest assets when it comes to teaching your child about shapes and spatial reasoning.

They’ll start out by learning about the basic 2-D shapes that are used in math: squares, triangles, circles, rectangles, rhombuses, and ovals. Learning how to draw these basic shape illustrations can be helpful for their learning process.

Some of these shapes you’ll be able to reference easily in your day-to-day life. This will help reinforce your child’s understanding of the shapes after their initial introduction.

For example, when making breakfast with your child, you could hold up a plate and ask them, “What shape is this? Do you think it’s a square or a circle?”

Other shapes, like triangles or rhombuses, may be a little harder to find hanging around. Challenge your child to find these shapes in nature. Are there any flower petals in your garden that are shaped like triangles (or an aloe vera plant hanging in their windowsill)?

Encourage your child to be creative with identifying shapes! It will help them with learning geometry in the long run.

Next, learning 3-D shapes will come after learning 2-D shapes. Like their flatter cousins, 3-D shapes are all around the world, too! Your child’s soccer ball is a sphere; the paper towel roll in the kitchen is a cylinder.

We recommend learning the basic form of these shapes and how they appear first. Then, you can use the natural 3-D shapes in your child’s environment to reinforce their learning!

Point out shapes when you see them and play a shape version of “I Spy” to practice. If your child has a set of blocks, talk about the different shapes of the blocks. Challenge them to use only one shape to build something. Then, see what they can make by using all of the shapes.

Kids also learn about spatial reasoning by discovering how to describe the shapes they see and play with. They can compare them with dimensional adjectives like “big” and “small,” or characteristics of their shape like “straight” and “curvy.”

This includes the spatial relationship between different objects, too. Look out for observations using location adverbs like “under,” “beside,” or “around.” These are all different ways for your child to “measure” or observe how shapes take up space.

4) Sorting And Patterns

We categorize things in our daily lives without even realizing it. Your child probably already does this, too — they may arrange their stuffed animals or toys in a certain way. For example, they may keep farm animals separated from dinosaurs.

Sorting and patterns are related to categorical reasoning. In the same way grocery stores sort out items by their parallel uses, your child will learn how to sort things based on their characteristics and how they are the same or different from other objects.

They’ll sort objects by weight, shape, quantity, texture, color, and other traits, often without even realizing it!

It’s important to note here that sorting and counting aren’t sequential. Your child might begin sorting before they begin counting, in fact.

For instance, if you want your child to sort a bowl of fruit, you can ask them to count all of the strawberries. They’ll sort the strawberries from the rest of the fruit. If you ask them to count the red fruit, they’ll sort out strawberries, cherries, and watermelon and count them together.

Once a child has learned to isolate characteristics, they can begin to identify, extend, and even create patterns. Your child will learn how to:

  • Copy a pattern
  • Identify the parts that repeat and continue a pattern
  • Correct a mistake in a pattern
  • Explain a pattern
  • Create their own patterns

To encourage your child to explore patterns, take a few moments to build a pattern for them when you play together. Use whatever materials you have available and create a simple AB pattern, such as truck, car, truck, car.

Next, point to each object. Say its name aloud. Then, when you get to the end of the row, ask them what comes next. If they aren’t sure, grab the next object and put it down. Once you’ve completed one round, start at the beginning and repeat each item to reinforce the pattern.

5) The Language Of Math

Part of learning how to do math means learning how to “speak” math. We don’t mean your child will turn into C-3PO — just that they will learn how to use mathematically correct language, or how to tell a story with math terms.

This can happen in daily life. While picking at an afternoon snack, your younger child may say, “Hey! My brother has more crackers than me!” Then you might agree to “add” to the cookies on the younger child’s plate so that both plates are “equal.”

These skills may be naturally exciting for your child — they’ll feel like they’re learning how to speak “grown up!” Show them how fun it is to incorporate mathematically appropriate language into their daily speech and use it to tell stories about what’s going on around them.

Using words to describe things in their lives will help them give ownership over ideas and observations. Motivate them to think about the order of the world around them and use different words to describe them, such as:

  • More than
  • Less than
  • Shape names
  • Light or heavy
  • Small or big

Mastering math language will help them in their quest to become robust mathematicians! It’ll also help them develop a strong vocabulary so they’re better prepared for kindergarten.

Basic Pre-K Math Checklist

Now that you know some of the concepts your child will be learning in pre-k math, let’s look at some of the skills they’ll build during this time.

  • Rote count to 10
  • Use one-to-one correspondence to count up to 10 objects and tell how many there are altogether
  • Recognize basic shapes (circle, triangle, square)
  • Understand the concept of quantity (more/less)
  • Sort objects by one characteristic
  • Understand and use directional terms, such as up, down, in, out
  • Pick what object goes next in a simple pattern

While these aren’t all of the math skills your child might learn in pre-k, they will give your child a solid mathematical foundation to build on in kindergarten. And they’re all skills you can practice in fun ways!



Pre-K Math Development

As your child grows and learns, they’ll work through three phases of mathematical development: concrete, representational, and abstract. They’ll likely be in the concrete stage at the beginning of pre-k.

During this phase, students need hands-on activities and real-world examples to help them understand mathematical concepts. This is why math manipulatives are so crucial in the early years. It’s also essential to present math concepts in a very concrete way during this stage.

For example, if you’re teaching your child about numbers, don’t just tell them that five is more than three. Instead, show them five objects and three objects, and let them count for themselves. This will help them understand the concept of more and less.

As your child continues to learn and practice a mathematical concept, they can move into the representational phase. Here, students can count pictures or images instead of actual objects. For example, they realize that numbers can be represented by lines or drawings.

Then, they’ll be ready to try the abstract stage. At this point, children understand that numbers can be represented by symbols. They don’t need manipulatives or visual aids to do math problems. They can start using numbers and symbols such as + or – to solve math problems.

The activities above will help your child to build their understanding of mathematical concepts so they can move through the different stages.

But, in pre-k, it’s important to focus on the process, not the answer. So don’t worry if your child doesn’t get the solution right away. Let them work through the problem and try to figure it out for themselves.

A strong foundation in pre-k math sets children up for success when they start kindergarten. By providing opportunities for them to explore and experiment with math, you can help them develop the skills they need to be successful in school and beyond.

9 Fun Pre-K Math Activities

Now that you’re clear on all of the exciting new math concepts your pre-kindergartener will be exposed to and what skills they’ll practice, let’s talk about some games and activities you can play at home to help your child hone them.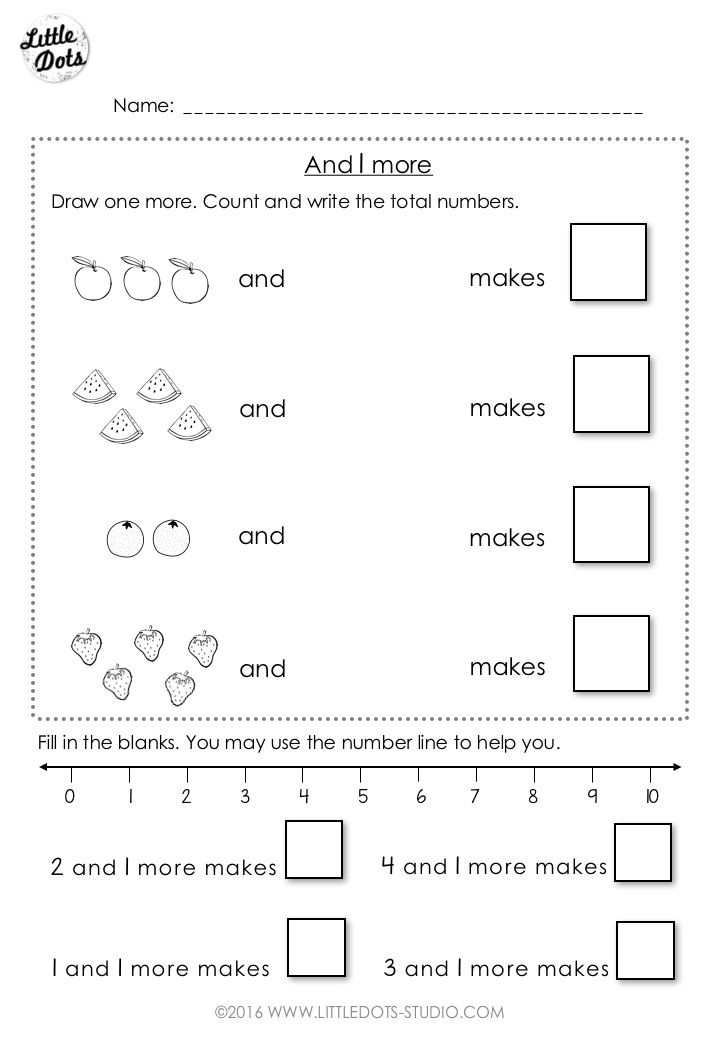

We’ve already discussed some math activities you can incorporate into everyday life. Now, we’re sharing our list of fun games to encourage your young learner to love math even more.

1) What Did I Do?

This game helps reinforce counting, adding, and subtracting. It’s quick to play, so it’s perfect for when you have a few extra minutes.

What You’ll Need
  • Small objects (e.g., paper clips)
What To Do

Place some paper clips (or any other small objects) in your hand, and let your child count how many you have. After they’ve done this, put your hands behind your back and either add or remove some.

Next, show your child the new quantity and ask them to count how many there are now. You can ask your child questions, such as, “Did I add or take away some paper clips?” or “How many did I add or take away?”

For even more fun and learning opportunities, take turns playing the game. And when it’s your turn to guess, it’s OK to guess wrong — “I think you took away 10!… No! I added two!” This back and forth offers lots of laughs and critical thinking for your little mathematician.

Remember that because your child is in pre-k, the concepts of addition and subtraction are still new. Therefore, it’s best to keep the number of objects used in this game low (e.g., 1-10 clips) so they aren’t confused or overwhelmed.

2) Math Tic-Tac-Toe

Add a mathematical twist to the classic game of Tic-Tac-Toe!

What You’ll Need
  • Paper
  • Pencil
  • Ruler
  • Markers (or colored pencils)
What To Do

Start by dividing your sheet of paper into squares by drawing lines (three horizontal by three vertical). In traditional tic-tac-toe, you’d leave these squares blank until the game starts. Not this time.

For this version of the game, you’ll need to fill each box with dots and have your child tell you how many dots are in a box before placing their X or O in it. The first player to get three Xs or Os wins!

The Xs or Os don’t have to be in order at this point, but you can add that requirement as a challenge once your child gets the hang of playing the game.

This activity helps kids work on their counting skills while also incorporating lots of fun.

3) NumberBow

Your child will add numbers to create a beautiful rainbow in this game.

What You’ll Need
  • Two dice
  • Two sheets of paper
  • Colored pencils (or crayons)
  • Pencil
What To Do

Draw two identical rainbow-shaped boards (one on each sheet of paper) with numbered boxes on the rainbows. (You can check out this link for reference.). The aim of the game is to color the numbered boxes in.

To play, each player throws two dice, then adds the numbers from the throw together and colors in the corresponding box on their rainbow.

For example, if your child throws a three and a one, they’d need to add 3+1 and color in the “4” box. If they’ve already colored that box in, they’d have to wait for their next turn. Each player gets 10 turns to have the most colorful rainbow at the end!

While this is an effective game to help your child work on their addition skills, some children might experience difficulty adding larger numbers together (e. g., 5 and 6). If you need to help them, that’s OK!

Remember that exposure and repetition are very beneficial for young learners.

4) Fill The Cup

This game can be challenging for younger children, so if it causes frustration, play other math games until your child is more comfortable with adding and counting.

What You’ll Need
  • Dice
  • Plastic cup
  • Small objects that are easy to count (e.g., paper clips, dried beans, pebbles, etc.)
What To Do

To begin the game, players roll the dice at the same time. The number rolled indicates the number of items you can add to your cup. For example, if you roll a five, you add five dried beans. The goal for your child is to be the first one to fill their cup.

At the pre-kindergarten stage, some children might not be comfortable with the steps needed to play this game (rolling the dice, reading the number aloud, adding the items to the cup). So, before starting, take a few minutes to get them used to the process.

If you notice that it’s still too challenging, you can make it easier by choosing to roll the dice for each other. In this option, you can roll the dice and then help your child read the number and add the right amount of items to their cup.

Whichever variation you choose, this is a fun and engaging way to help children learn numbers and practice counting.

5) Stand Up, Sit Down

Kids enjoy playing this active game where they get to use their bodies and their brains! (Note: This game requires more than one child player, so it’s a great activity for siblings or to do when your child has a friend over.)

What You’ll Need
  • Index cards
  • Marker
What To Do

Write the numbers 1-10 on the index cards (one number per card) and hand three to each participant. Then, say a math equation (or word problem) out loud.

If the answer matches a number they’re holding, the child will stand. If they don’t have the answer, they remain seated.

For example, if the question is, “If I have three dried beans and I throw away one, how many do I have left?”, the child with “2” would then need to stand up and show their card.

The player who has the least number of cards left at the end of five rounds wins. Note: To make it easier, you can give children small items (e.g., blocks, dried beans, paper clips, etc.) to help them count.

Stand Up, Sit Down is also helpful for children learning shapes. Instead of writing numbers on the cards and handing them out, you can draw different 2-D and 3-D shapes that children learn in pre-k (as discussed above) and hand those out.

To play, someone describes a shape and the player who has that shape stands up and says what it is. For example, “If you are holding a shape that has three sides, stand up right now!”

When the child stands up, they’ll need to say that their shape is a triangle, and they get the point. In this version of the game, the player with the most points at the end wins.

Using this game allows children to learn the names and attributes of the different 2-D and 3-D shapes they get exposed to in pre-kindergarten.

6) Who Has More?

This game is perfect for helping kids understand the concepts of more and less, which are critical in early math development.

What You’ll Need
  • A small bowl or container
  • A teaspoon
  • A handful of objects (e.g., buttons, pennies, cereal pieces, etc.)
What To Do

Place the objects in one bowl. Have your child scoop a teaspoon of them out and count them. Then, you do the same and see who got the most. That person’s the winner!

Note: Counting past 10 is difficult at this age, so you’ll want to use big enough items (such as large kidney beans) and stick to a teaspoon for scooping so your child doesn’t end up with more than 10 per spoonful.

7) Read Math Books

Help your child develop a love for math by reading math-related books together.

What You’ll Need
  • A mathematical-themed book to read together (see some recommendations below)
What To Do

Grab one of the following books and snuggle up with your little one for a math-themed storytime. As you read, point out any mathematical concepts in the book.

  • From the Garden by Michael Dahl
  • The Shape of Me and Other Stuff by Dr. Seuss
  • The Button Box by Margarette S. Reid
  • A Pair of Socks by Stuart J. Murphy
  • The Berenstain Bears and the Spooky Old Tree by Stan and Jan Berenstain
  • Pattern Fish by Trudy Harris

When you finish reading, discuss any new math concepts your child learned. You could even do a related activity or two to reinforce what they’ve learned.

8) In The Box

This game helps your child practice prepositions or direction words, like “under,” “behind,” and “in front of.” These concepts are essential for mathematical development as well as reading comprehension.

What You’ll Need
  • A stuffed animal
  • An empty box large enough for the animal to fit inside
What To Do

Ask your child to put the animal inside the box. If they have difficulty understanding what you mean, give them some clues. For example, you could say, “Put the animal in the box so that its head is sticking out,” or “Put the animal in the box so that only its tail is showing.”

Once the animal is in the box, ask them to describe where it is using prepositions. So, they might say, “The animal is in the box.”

Then, take the animal out and place it behind the box. Ask your child to describe its location again. For example, they might say, “The animal is behind the box.”

Next, let them take a turn placing the animal in, on, under, next to, etc. the box. When they’re done, you describe where it is. Continue taking turns as you practice different prepositions.

9) Number Line Race

This game helps kids with number recognition as well as one-to-one correspondence.

What You’ll Need
  • Number cards (we recommend the ones from the HOMER Explore Numbers Kit)
  • A die
What To Do:

Spread the cards out in numerical order, with a bit of space between each one. They should form a line on the floor, though it doesn’t need to be perfectly straight.

Have your child stand on the card with the number one on it. Hand them the die and let them roll it. Call out the number they rolled. Next, ask them to move that many numbers forward, moving from one index card to the next as they count aloud.

If they land on a number that would take them off the end of the line, they start from the beginning for their next throw (each player gets five throws). Then, it’s your turn! Start on one and see how far you can get, too.

The person to end on the card with the highest number is the winner!

Encouraging A Love Of Pre-K Math At Home

Pre-k math isn’t just reserved for pre-k classes. You can help your child explore the exciting world of pre-k math right from your home!

HOMER is always here to help and happy to be your at-home learning partner. Our Learn & Grow app offers tons of opportunities for your child to develop their pre-k math skills from conception to execution.

Our games are personalized to accommodate your child’s specific interests. They include pattern-identification games like Ribbons or shape-building games like the Castle Creator.

Your child can also explore the Shapery Bakery, where they help the cute, cuddly Tisa the Cat by sorting treats based on their shape. All that and so much more can help your child develop their pre-k math skills!

Author

The concept of the development of mathematical education in the Russian Federation

January 23, 2014 in the large hall of the mayor's office of the city of Yaroslavl, a round table "Psychological and pedagogical support of the educational process: mathematical education and thinking" was held. Representatives of educational authorities took part in its work; administration, mathematics teachers, educators, senior methodologists, educational psychologists; university representatives.

The development of mathematical education is one of the priorities of the state policy in the field of education and is considered as an area of ​​potential leadership of the country and regions. In pursuance of the May Decrees of the President, on December 24, 2013, the Government of the Russian Federation approved the Concept for the Development of Mathematical Education in the Russian Federation. The purpose of the concept is to bring Russian mathematical education to a leading position in the world. Mathematics should become an advanced and attractive field of knowledge and activity.

The concept is aimed at the development of mathematical education at all levels of Russian education (preschool, general, professional). It is recognized that mathematics plays a system-forming role, developing cognitive abilities, logical, conceptual thinking, influencing the study of other disciplines.

On behalf of the Governor of the region, the Yaroslavl Mathematical School project is being implemented. The project is aimed at identifying talented children, creating resource centers for mathematicians in the municipal districts of the region, methodological support for teachers working with gifted mathematicians, and one of its directions was the creation of the Yaroslavl Mathematical Club.

The city of Yaroslavl has a long and rich tradition of mathematical education. Yaroslavl schools prepare strong mathematicians who participate in international mathematical competitions and enter the best universities. Thus, since 2001, students of school No. 33 have won 9 international olympiads in mathematics, and 5 times have won gold. In 2013, Nadezhda Vlasova, a student of school No. 36, won silver at the Open Chinese Mathematical Olympiad for Girls (CGMO - an international mathematical competition held since 2001). Therefore, it is no coincidence that Yaroslavl teachers begin an open professional discussion of ways to develop mathematical education, both at the municipal level and at the regional level.

Within the framework of the round table, the problems of mathematical education in the Yaroslavl region, the influence of mathematics on the development of students' thinking, the formation of spatial representations in preschool age as the basis for the development of mathematical thinking, the competence of a mathematics teacher in modern conditions of educational development were considered.

The Concept for the Development of Mathematics Education in the Russian Federation

Action Plan for the implementation of the Concept for the Development of Mathematics Education

Mathematical development of preschool children, development of logic (consultation for teachers) .

"Developing Mathematical Ability in Preschoolers" (Parental Advice)

Advice for Parents Preschool Children "Play with Kuizener's Sticks"

Math fun In the preparatory group on the “Riddles of the Queen of Sciences”

Mathematical centers in groups

Concept of mathematical education in preschool education

Senior teacher No. 10 “OTC LIK” kindergarten No. 16, Samara Region, Otradny

Stulnikova O.G. The concept of mathematical development in preschool education // Sovushka. 2018. N3 (13). URL: https://kssovushka.ru/zhurnal/13/ (date of access: 04.12.2022).

Order No. 116698

The concept determines the ratio of pre-mathematical and pre-logical components in the content of education. The predicted results depend on this ratio: the development of the intellectual abilities of children, their logical, creative or critical thinking; the formation of ideas about numbers, computational or combinatorial skills, ways to transform objects, etc.

Acquisition of knowledge and skills is formed under the influence of developing education and due to the special organization of the educational process, all cognitive mental processes associated with sensation, perception, memory, attention, speech, thinking, as well as volitional and emotional processes in general, develop. The developing effect of training should be focused on the “zone of proximal development”. Children are offered, along with tasks that they can now perform on their own, and such tasks that require them to guess, ingenuity, and observation. The knowledge acquired in this way, and most importantly, the systematic improvement of their quality, plus the development of thinking, ensure the overall development of the child.

The process of mathematical development

The process of a child's mathematical development is connected, first of all, with the development of his cognitive sphere (various ways of cognition, cognitive activity, etc.), as well as with the development of the mathematical style of thinking.

Thanks to mathematical development, preschoolers develop personal qualities: activity, curiosity, perseverance in overcoming difficulties, independence and responsibility. In the process of mathematical development, the general intellectual and speech development of the child takes place (evidence-based and reasoned speech, dictionary enrichment).

The purpose of the mathematical development of a preschooler is to get acquainted with the basics of mathematical culture and instill interest in further knowledge of the world around us using elements of this culture (Decree of the Government of the Russian Federation "On approval of the Concept for the development of mathematical education in the Russian Federation", December 2013).

Basic tasks of mathematical development:

  • Formation of skills and abilities in counting, calculations, measurement, modeling. 9009one
  • Development of logical and mathematical concepts and ideas about the mathematical properties and relationships of objects, specific quantities, numbers, geometric shapes, dependencies and regularities.
  • Development of sensory (object-effective) ways of knowing mathematical properties and relationships, namely, survey, comparison, grouping, ordering.
  • Development in children of logical ways of knowing mathematical properties and relations, namely, analysis, comparison, generalization, classification, seriation.

General didactic principles of teaching preschoolers the elements of mathematics

The principle of nurturing education.

Upbringing and education - educative education, characterized by concrete mental and practical work of children, which develops their organization, discipline, accuracy, responsibility.

The level of development of a preschooler depends on a specially organized "mental education", which is a pedagogical process aimed at developing elementary knowledge and skills, methods of mental activity in preschoolers, as well as developing the abilities of children and their need for mental activity. The main component of the mental education of a preschooler is the methods of mental actions. Each mental action is a corresponding mental operation. These operations are different, interrelated, passing into each other aspects of thinking.

Basic mental operations: analysis, synthesis, comparison, classification, generalization, abstraction . All of these operations cannot occur in isolation without connection with each other, i.e. it is impossible to form separately any mental operation without connection and reliance on other operations. “An indicator of the assimilation of a technique is its conscious transfer to the solution of new problems.” In a preschooler, the methods of mental actions should be laid down precisely at this age, moreover, without the formation of mental operations, the mental upbringing of a child is impossible.

The principle of humanization of the pedagogical process.

This is the principle of a personality-oriented model of education and training.

The main thing in education should be the development of the ability to acquire knowledge and skills and use them in life, the individualization of education, the creation of conditions for the development of the child as a person.

The principle of individual approach.

The principle of an individual approach provides for the organization of education based on a deep knowledge of the individual abilities of the child, creating conditions for the active cognitive activity of all the children of the group and each child individually.

The principle of scientific education and its accessibility.

This principle means the formation of elementary, but, in fact, scientific, reliable mathematical knowledge in preschool children.

Ideas about quantity, size and shape, space and time are given to children in such volume and at such a level of specificity and generalization that it is accessible to them, and that this knowledge does not distort the content, taking into account the age of children, the peculiarities of their perception, memory, attention, thinking.

The implementation of the principle of accessibility is also facilitated by the fact that the material being studied is presented in accordance with the rules: from simple to complex; from the known to the unknown; from general to specific.

Thus, children's knowledge is gradually expanding, deepening, they are better absorbed, but new knowledge should be offered to children in small doses, ensuring repetition and consolidation of them with different exercises using their application in different types of activities.

The principle of accessibility also provides for the selection of material that is neither too difficult nor too easy. When organizing the education of children, the teacher must proceed from the available level of difficulty for children of a certain age.

The principle of awareness and activity.

Conscious assimilation of educational material provides for the activation of mental (cognitive) processes in a child.

Cognitive activity is independence, awareness, meaningfulness, initiative, creativity in the process of mental activity, the ability of a child to see and independently set cognitive tasks, draw up a plan and choose ways to solve a problem using the most reliable and effective methods, achieve results.

The principle of systematicity, consistency.

The logical order of learning material, in which knowledge is based on previously acquired knowledge. This principle is especially important in the study of mathematics, where each new knowledge, as it were, follows from the old, known. The teacher distributes the program material in such a way as to ensure its consistent complication, the connection of subsequent material with the previous one. It is this study that provides solid and deep knowledge.

The principle of visibility.

the child's thinking is predominantly visual-figurative in nature. In the methodology of teaching children mathematics, the principle of visibility is closely associated with the activity of the child. Conscious mastery of the elements of mathematical knowledge is possible only if children have some sensory cognitive experience, through direct perception of the surrounding reality or knowledge of this reality through visual and technical means.

Object-spatial environment

Successful work requires a specially organized object-spatial developing environment: a room with both a place for children to work at tables and enough space for games, including mobile ones. Availability of a game library, materials for the manufacture of games and game material. The presence of balls, cubes and other physical education equipment.

Principles of organizing the educational process

For the organization of the educational process, a three-block model has been chosen, which combines all the known basic models by which preschool institutions operate: educational, complex-thematic, subject-spatial - environmental. In this case, the strengths of each individual model are used, and, if possible, their shortcomings are eliminated.

Block I Specially organized training in the form of classes - the content is organized by "subjects".

II block. Joint adult - children's (partnership) activities - the content is organized in a complex - thematic way.

III block Free independent activities of children - in accordance with the traditional types of children's activities.

Within the framework of the first block, training is organized in the form of special lessons based on the program. The process of teaching preschoolers is built taking into account the age characteristics of preschool children. Playing techniques and means are mainly used, activities that are attractive to children (the principle of “learning with passion” is implemented), a combination of voluntary and involuntary, static and dynamic forms in the classroom that is comfortable for the psychophysiological state of the child is provided.

Within the framework of the second block, cognitive and research activities of children are organized on the basis of standards. The goal is to help students learn how to independently acquire knowledge, develop research skills, form a holistic picture of the world and understand their place in it. In the course of research, pupils: conduct experiments and practical work; collect information and process data; make projects and make presentations;

As part of the third block, independent activities of children are carried out in the classroom in activity centers and in arbitrary play activities.

The activity is aimed at developing the cognitive abilities and search activities of children. In the activity centers, the room is divided into several zones, each of which contains materials for classes, games, experiments and research.

The role of preschool preparation for school is indisputable not only in the formation, development and replenishment of mathematical knowledge, skills and abilities of a preschooler, but also in the intellectual development of the child as a whole. Mathematical education in the early stages of development is a powerful tool for the formation of a person with developed logical thinking, skills of analysis and synthesis, classification and systematization.

These skills will be the key to success not only in school mathematics, but also in other subjects of the school cycle, and in the future professional activities of a growing citizen. The preparation of the basis of mathematical knowledge should take an important place in the programs of preschool education and training.

Literature

  1. Alytkhauz D.

    Learn more