Math skills kindergarten
Math Skills for Kindergarten, What Your Child Will Learn, Komodo Math
- Math Tips
- Education
- K
As your child heads into kindergarten, you’ll be feeling all sorts of emotions. You may be wondering: How can my baby be that old? Is she ready? What exactly is he going to learn in kindergarten?
While kindergarten may have changed since you were a child, it still forms the foundation of your child’s schooling and we wrote earlier about how to prepare for a successful start to the school adventure.
In math, students will learn the basics of how numbers work while exploring place value and the concepts of addition and subtraction.
But there’s no need to figure everything out as your child does - this article will help you get a head start by knowing what to expect.
In kindergarten your child will learn how to:
1.
Going into the school year, your child may be able to orally count to 10 or beyond. By the end of kindergarten, expect that counting to advance to 100. But don’t worry, we’re only talking about counting orally. Your kindergartner will not be expected to write all the numbers to 100.
In most kindergarten classrooms, teachers count the days of school with the children. By counting each day, children gradually become more fluent with bigger and bigger numbers. At the end of 100 days, kindergarten classrooms often have a big celebration with many more opportunities for counting.
At home: To support your child’s counting skills, encourage your kindergartner to count as high as possible. This is a great task to give your child in the car - or even at bedtime!
2. Answer “how many?” questions about groups of objects
As well as counting to 100, kindergartners will be asked to count how many objects are in a group.
Students need to be able to physically count objects one at a time, assigning one number to each object as they count. This is a skill called one-to-one correspondence.
At home: Ask children to tell you how many toys they are playing with and watch how they keep track of each object that is counted. If your kindergartner counts the same object twice or skips an object, encourage another try.
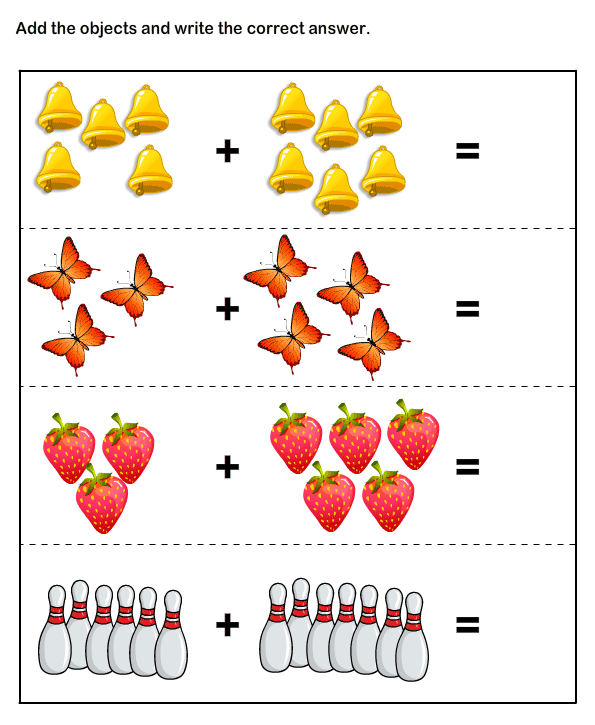
3. Solve basic addition and subtraction problems
In kindergarten, children start to develop an understanding of addition and subtraction within 10. Kindergartners start by solving problems involving physical objects, and as the year goes on, students learn to draw pictures to represent addition and subtraction problems. They will even begin to solve simple word problems.
At home: Present two groups of blocks (less than 10 in all) and have your child add the blocks together. As your child develops understanding, you can ask simple addition or subtraction problems without using the physical objects as a support.
4. Understand the numbers 11-19 as a ten plus some ones
Though it may seem quite advanced, your kindergartner will begin to understand the concept of place value and that position makes some numbers bigger than others - ie get to grips with the idea that 21 is bigger than 12. Students may use place value blocks to be able to “see” how ten ones become a ten.
At home: When counting blocks or lego bricks at home, make a group of ten. Then add on extra “ones” to make the numbers 11-19. You can even talk about place value when looking at written two-digit numbers.
5. Name shapes
Kindergartners will learn about 2D and 3D shapes. They should be able to name different shapes while describing their features. Kindergartners love to recognize shapes in the real world!
At home: Help your child by having them spot squares, cubes, spheres, rectangles, etc.
Challenge your kindergartener to draw pictures using basic 2D shapes, then talk to you about the drawings. Making and continuing shape patterns is another fun way to help engage your kindergartner as they learn about shapes.
Throughout the year, make sure to ask your child about what’s happening in kindergarten math. Give your child an opportunity to teach you by sharing what he or she has learned. Get ready for a fun year in kindergarten!
Found this useful? Check out our grade by grade math guides from Kindergarten to 5th grade
Written by Lily Jones, Lily loves all things learning. She has been a kindergarten & first grade teacher, instructional coach, curriculum developer, and teacher trainer. She loves to look at the world with curiosity and inspire people of all ages to love learning. She lives in California with her husband, two kids, and a little dog.
About Komodo – Komodo is a fun and effective way to boost K-5 math skills.
Designed for 5 to 11-year-olds to use in the home, Komodo uses a little and often approach to learning math (15 minutes, three to five times per week) that fits into the busy family routine. Komodo helps users develop fluency and confidence in math – without keeping them at the screen for long.
Find out more about Komodo and how it helps thousands of children each year do better at maths – you can even try Komodo for free.
Back to School - 5 Tips to Help you Ease Back into the Routine
Here are some steps you can take to ease children back from full vacation mode so that the first week of school doesn't knock you sideways.
Mindset - The Path to Mastery
People who have a growth mindset believe that they always have the potential to learn and improve. They are more motivated to persevere with difficult tasks, to take risks and to learn from failure.
Important math skills for kindergarten
Want to help your kindergartner master math? Here are some of the skills your child would be learning in the kindergarten classroom.
Numbers
Words and numerals for numbers
Know the words for numbers (“one,” “two,” “three,” “four” for 1, 2, 3, 4) through 20. Write numbers from 0 through 20.
Counting to 100
Count to 100, by ones and by tens.
Tip: Incorporate basic math concepts.
Try to incorporate basic math concepts into everyday activities. Have your child count objects regularly and pose easy counting challenges, such as counting the number of steps on a flight of stairs or the number of red cars you see while driving. Take opportunities to count by twos or fives or tens, for example if you’ve bought many of the same item at the grocery store or need to count a pile of coins.
Counting objects in groups
Count how many objects are in a group (to 20).
By counting or matching objects, tell whether the number of objects in one group is greater than (more) or less than (less), or equal to (the same as) the number of objects in another group.
Comparisons between small numbers
Compare any two numbers between 1 and 10, and tell which is greater than or less than the other.
Understanding numbers 11 - 19
Understand numbers 11 through 19 as ten ones and some additional ones.
Addition, subtraction, multiplication, & division
Addition & subtraction
Understand addition as “putting together” and “adding to.” Understand subtraction as “taking apart” and “taking away from.”
Tip: Apply math to everyday life.
It's especially memorable to children when they can use their new math concepts in their everyday life. Have your child arrange their favorite stuffed animals in a circle for a party and give two or three crackers to each toy. Have them add up the total number of crackers distributed.
Ask them to predict how many more crackers they would need if one of their toy action figures joined the party. Then ask them to predict the total number of crackers needed with yet another guest. This gives them an opportunity to "add up" in their head and then see if they are correct when they actually add the next figure and counts up the new total. The game can be played in reverse when one of the figures leaves the party, taking their crackers with them.
Master adding and subtracting
Add and subtract within 5 (1 to 5) quickly and accurately.
Solving word problems
Using objects, fingers, simple math drawings, or mental images, solve addition word problems involving numbers that add up to 10 or less, and subtraction word problems involving subtraction from 10 or less.
Adding to 10
For any number, 1 through 9, find the unknown number (quantity) needed to total 10. Show the answer with a drawing or equation (number sentence).
Breaking up numbers
Break up numbers, 3 through 10, into pairs, in more than one way.
Measurement & data
Measuring in different ways
Understand that objects can be measured in different ways: length (“how long”), height (“how high” or “how tall”), and weight (“how heavy”). Compare the length, height, and/or weight of two objects.
Relative position of objects
Describe the relative position of objects – for example, above, below, in front, behind.
Shapes
Naming common shapes
Name common shapes, such as squares, rectangles, circles, triangles. Describe common shapes in simple terms: “Circles are round.” “Triangles have three sides.”
Tip: Practice shape recognition.
Practice recognition of different shapes. Have your child spot things that are triangular, like pieces of pizza or the roof of a house, or rectangular, like paper money. As you talk about different shapes, have them describe why a shape they spot is a triangle (three sides) or a square (four equal sides) or a rectangle (two opposite equal sides and two other opposite equal sides of longer length).
Understanding flat and solid shapes
Understand the difference between “flat” or two-dimensional shapes (a square or circle drawn on paper) and “solid” or three-dimensional shapes (a wooden block or cube; a sphere or globe).
Creating shapes
Use building and drawing to create shapes.
For tips to help your kindergarten in math class, check out our kindergarten math tips page.
TODAY's Parenting Guides were developed by NBC News Learn with the help of subject-matter experts, and align with the Common Core State Standards.
Parent Toolkit Staff
Parent Toolkit is a one-stop resource for parents produced by NBC News Learn.
90,000 to develop mathematical skills in preschoolers through gamesMove to the content of
Rigakids - Information section - Development of mathematical skills in preschoolers in kindergarten through games
- 25,0008
- 200007 2021
The development of mathematical skills in a child through games is gaining more and more popularity.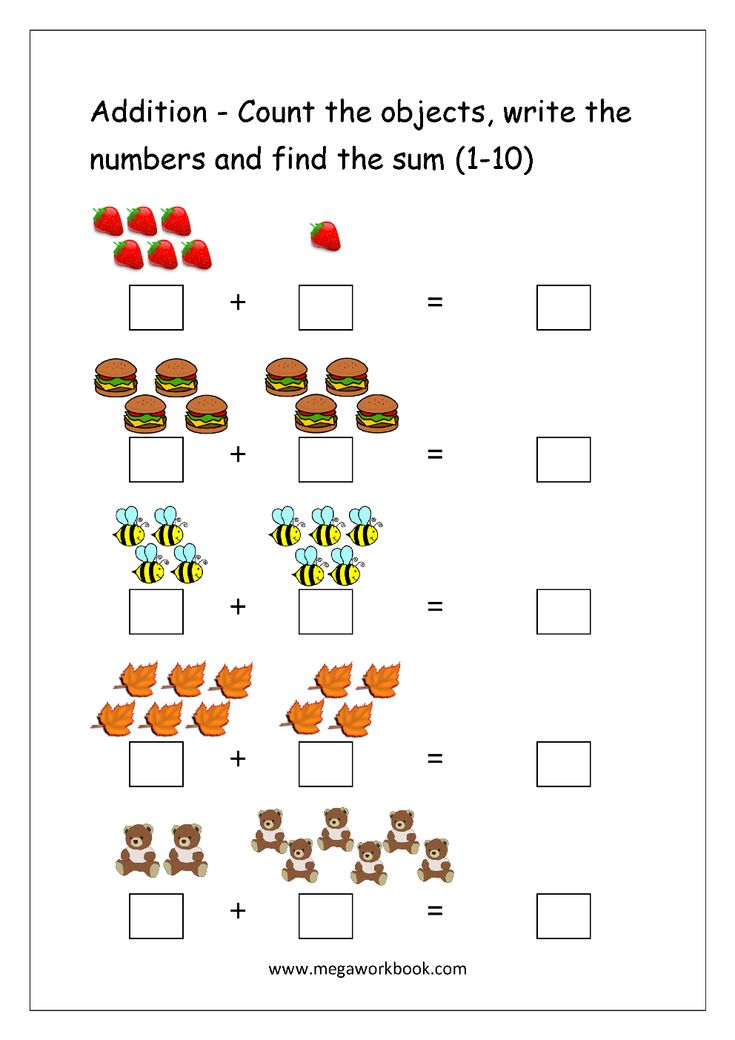
Many well-known private kindergartens, including ours, use this approach in teaching mathematics.
But why? What are the advantages of this method? Why is it better to use it, and not some other? Let's look into these issues!
Why is it best to teach a preschooler mathematics through games?
No one will argue with the fact that any education should be appropriate for the child's age.
At preschool age, children think differently than in their school years.
Play is essential for a child, especially under the age of 7. Even in the first years of schooling, children still have a huge need for games. For some, this need does not disappear even in old age.
Why do children like games so much? What is so special about games?
The charm of play for a child lies primarily in the fact that there is no real conditionality in it. The child himself creates the rules and his own reality. From the creator of the world that he invented for himself.
Mathematical or didactic games are based on this technique.
How does the development of mathematical skills through games work?
All tasks are given to the child in an exclusively playful way.
Through a variety of practical activities, children gain skills in counting, measuring and calculating without even knowing it.
Any didactic game contains two components: for yourself, mastering the skills.
Depending on which game is used, different types of influence on the child's consciousness are carried out. Two main ones can be distinguished.
Namely:
- the game is built in such a way as to surprise at the very beginning and thus motivate to go on with the process
- "search and discovery" the child masters the cause-and-effect relationship and perceives learning as a quest
No matter how the game is built, its main essence is to fill learning with emotional and cognitive content and cause joy.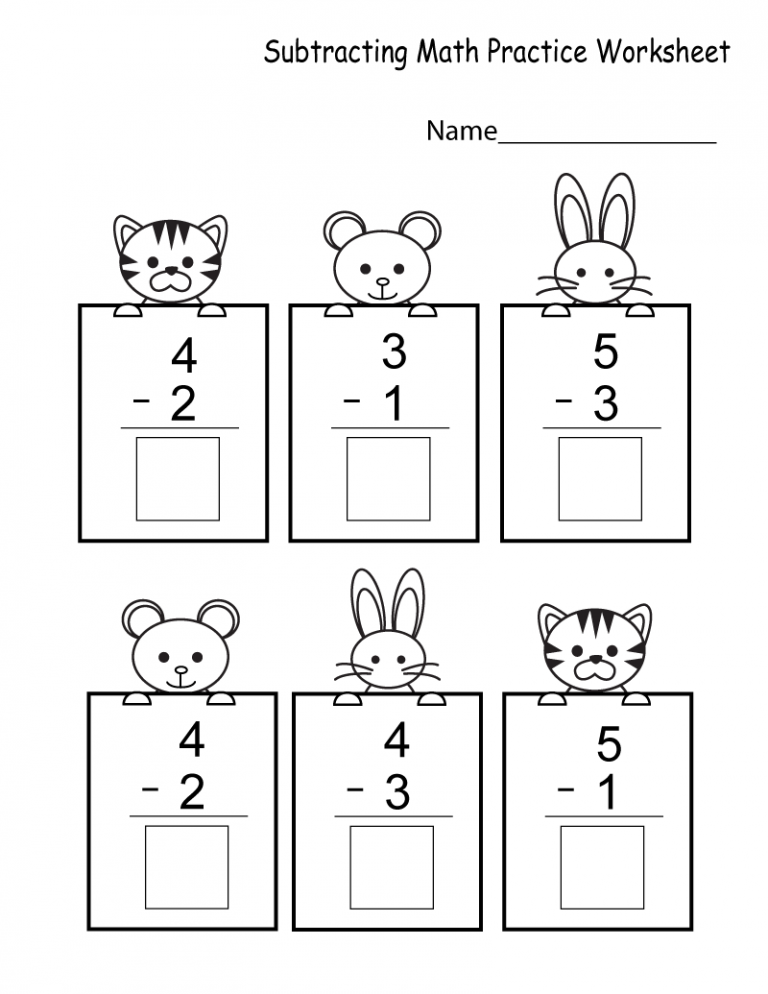
How do we teach mathematics to preschoolers in RigaKids kindergartens?
RigaKids pays special attention to teaching math skills. Our methodologists have developed a program based on the most modern approaches and the latest research in the field of preschool development.
⠀
Also, we don't have boring classes!
⠀
🏰 RIGA KIDS - a network of bilingual kindergartens
Other entries:
"Methods and techniques for the formation of elementary mathematical representations among preschoolers" - JV "Kindergarten No. 2, secondary school No. 30, Syzran"
Message on the topic:
“Methods and techniques for the formation of elementary mathematical representations in preschoolers”
Mathematical knowledge of a preschooler is a directly important basis in the mental development of a child. Thanks to mathematical knowledge, children learn to: analyze, compare, synthesize, perform computational operations, think logically, distinguish between geometric shapes, name their features, navigate in space.
Preschool children develop memory, attention, thinking. The knowledge gained in kindergarten, children apply in everyday life. Therefore, the task of the teacher: to arouse children's interest in educational activities, to give the necessary elementary mathematical knowledge, to lead children to independent answers, search for solutions. The teacher must find an approach to each child and give this knowledge to all children.
Methods and techniques for the formation of mathematical representations in preschoolers.
In the process of forming elementary mathematical concepts in preschoolers, the teacher uses a variety of teaching methods:
- practical,
- visual,
- verbal,
- gaming.
When choosing a method, a number of factors are taken into account:
program tasks to be solved at this stage;
age and individual characteristics of children;
availability of the necessary teaching aids, etc.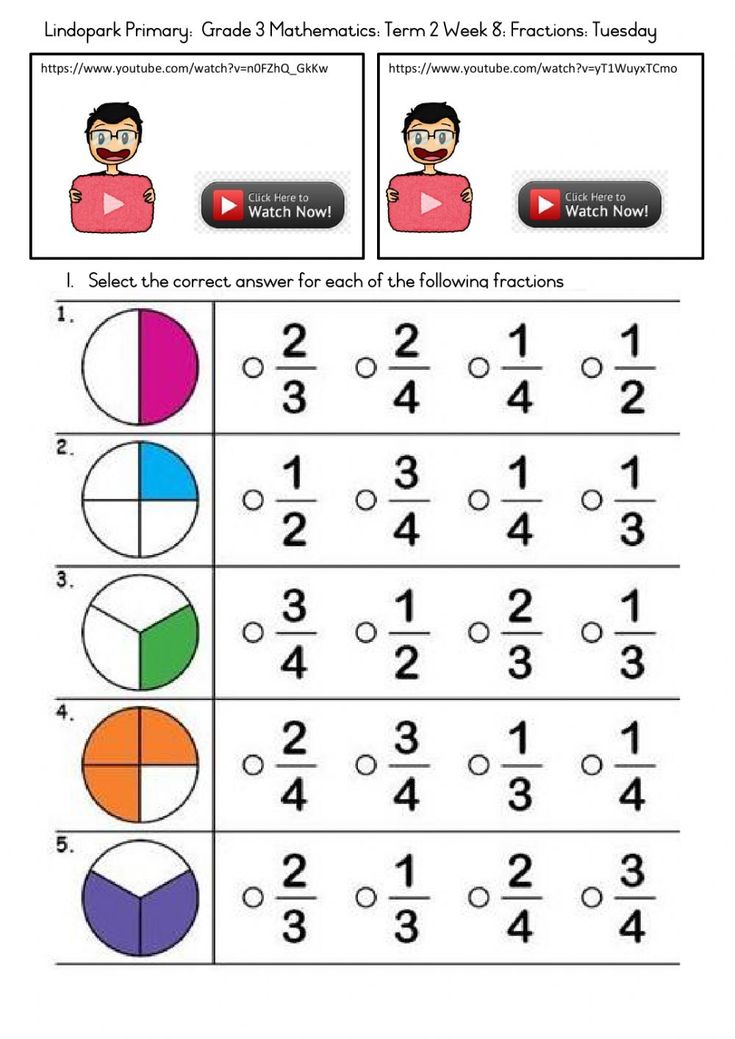
;
The teacher's constant attention to a reasonable choice of methods and techniques, their rational use in each specific case ensures:
— successful formation of elementary mathematical concepts and their reflection in speech;
- the ability to perceive and highlight relations of equality and inequality (by number, size, shape), sequential dependence (decrease or increase in size, number), highlight quantity, shape, size as a common feature of the analyzed objects, determine relationships and dependencies;
- orientation of children to the application of the mastered methods of practical actions (for example, comparison by comparison, counting, measurement) in new conditions and an independent search for practical ways to identify, detect signs, properties, and connections that are significant in a given situation. For example, in the conditions of the game, to identify the sequence, the pattern of alternation of features, the commonality of properties.
The leading method in the formation of elementary mathematical concepts is a practical method.
Its essence lies in the organization of children's practical activities aimed at mastering strictly defined methods of action with objects or their substitutes (images, graphic drawings, models, etc.).
Characteristic features of the practical method in the formation of elementary mathematical representations:
— performance of various practical actions;
— wide use of didactic material;
- the emergence of ideas as a result of practical actions with didactic material:
- development of counting skills, measurement and calculation in the most elementary form;
- wide use of formed ideas and mastered actions in everyday life, play, work, i.e. in various types of activity.
This method involves the organization of special exercises that can be offered in the form of an assignment, organized as actions with demonstration material, or proceed as independent work with handout didactic material.
Exercises can be collective - they are performed by all children at the same time, and individual - they are carried out by an individual child at the teacher's board or table.
Collective exercises, in addition to mastering and consolidating knowledge, can be used for control.
Individual, performing the same functions, also serve as a model for which children are guided in collective activities.
Game elements are included in the exercises in all age groups: in the younger ones - in the form of a surprise moment, imitation movements, a fairy-tale character, etc.; in seniors, they acquire the character of a search, a competition.
From the point of view of children's manifestation of activity, independence, creativity in the process of performance, reproductive (imitative) and productive exercises can be distinguished.
The game as a method of teaching and the formation of elementary mathematical representations involves the use in the classroom of individual elements of different types of games (plot, mobile, etc.), game techniques (surprise moment, competition, search, etc. Currently a system of so-called learning games has been developed.
0003
All didactic games on the formation of elementary mathematical representations are divided into several groups:
- Games with numbers and numbers
- Time travel games
- Orientation games in space
- Games with geometric figures
- Games for logical thinking
Visual and verbal methods in the formation of "elementary" mathematical representations are not independent, they accompany practical and game methods.
Techniques for the formation of mathematical representations.
Kindergarten widely uses methods related to visual, verbal and practical methods and applied in close unity with each other: This is the main method of teaching, it has a visual-practical-effective nature, is performed using a variety of didactic means, makes it possible to form skills and abilities in children. It has the following requirements:
- clarity, dissection of the display of methods of action;
- coordination of actions with verbal explanations;
- accuracy, brevity and expressiveness of speech accompanying the show:
- activation of children's perception, thinking and speech.
- Manual for self-exercises. This technique is connected with showing the educator methods of action and follows from it. The instruction reflects what and how to do in order to get the desired result. In the older groups, the instruction is given in full before the start of the task, in the younger ones it precedes each new action.
- Explanations, explanations, instructions. These verbal devices are used by the educator when demonstrating a method of action or in the course of performing a task by children in order to prevent errors, overcome difficulties, etc. They should be specific, short and figurative.
Demonstration is appropriate in all age groups when getting acquainted with new actions (application, measurement), but it requires activation of mental activity, excluding direct imitation. During the development of a new action, the formation of the ability to count, measure, it is desirable to avoid repeated display.
Mastering the action and improving it is carried out under the influence of verbal techniques: explanations, instructions, questions. At the same time, the speech expression of the mode of action is being mastered.
- Questions for children.
Questions activate the perception, memory, thinking, speech of children, provide comprehension and assimilation of the material. When forming elementary mathematical representations, a series of questions is most significant: from simpler ones aimed at describing specific features, properties of an object, the results of practical actions, i.e., ascertaining, to more complex ones that require establishing connections, relationships, dependencies, their justification and explanation, use the simplest proofs.
Most often, such questions are asked after the educator demonstrates the sample or the children complete the exercises. For example, after the children have divided the paper rectangle into two equal parts, the teacher asks: “What did you do? What are these parts called? Why can each of these two parts be called a half? What shape are the parts? How to prove that the squares are obtained? What should be done to divide the rectangle into four equal parts?
Basic requirements for questions as a methodological device:
- accuracy, concreteness, conciseness:
- logical sequence;
— variety of formulations, i.
e. the same question should be asked in different ways
— optimal ratio of reproductive and productive questions depending on the age of the children and the studied material;
- give children time to think;
- the number of questions should be small, but sufficient to achieve the didactic goal;
- prompting questions should be avoided.
The teacher usually asks the whole group a question, and the called child answers it. In some cases, choral responses are possible, especially in younger groups. Children need to be given the opportunity to think about the answer.
Children's answers should be:
- short or complete, depending on the nature of the question;
- independent, conscious;
- accurate, clear, loud enough;
- grammatically correct (observance of the order of words, the rules for their agreement, the use of special terminology).
In working with preschoolers, an adult often has to resort to the method of reformulating an answer, giving it a correct sample and offering to repeat it. For example: “There are four mushrooms on the shelf,” says the baby. “There are four mushrooms on the shelf,” the teacher clarifies.
- During the formation of elementary mathematical concepts in preschoolers comparison, analysis, synthesis, generalization are not only
as cognitive processes (operations), but also as methodological techniques that determine the path along which the child's thought moves in the process of learning.
Comparison is based on establishing similarities and differences between objects. Children compare objects by quantity, shape, size, spatial arrangement, time intervals by duration, etc.
Analysis and synthesis as methodological devices act in unity. An example of their use is the formation in children of ideas about "many" and "one", which arise under the influence of observation and practical actions with objects.
- Modeling is a visual and practical technique that includes the creation of models and their use in order to form elementary mathematical concepts in children. Reception is extremely promising due to the following factors:
- the use of models and modeling puts the child in an active position, stimulates his cognitive activity;
- the preschooler has some psychological prerequisites for the introduction of individual models and elements of modeling: the development of visual-effective and visual-figurative thinking.
Models can play different roles: some reproduce external connections, help the child to see those that he does not notice on his own, others reproduce sought-for but hidden connections, properties of things that are not directly perceived.
Models are widely used in the formation of
- time representations: model of parts of the day, week, year, calendar;
- quantitative; numerical ladder, numerical figure, etc.
), spatial: (models of geometric shapes), etc. - when forming elementary mathematical representations, subject, subject-schematic, graphic models are used.
- Experimentation is a method of mental education that provides the child with self-identification through trial and error of connections and dependencies hidden from direct observation. For example, experimentation in measurement (size, measurement, volume).
- Monitoring and evaluation .
These techniques are interrelated. Control is exercised through monitoring the process of children performing tasks, the results of their actions, and responses. These techniques are combined with instructions, explanations, explanations, demonstration of methods of action for adults as a model, direct assistance, and include the correction of errors.
Methods and results of actions, behavior of children are subject to evaluation. The assessment of an adult who teaches to be guided by a model begins to be combined with the assessment of comrades and self-esteem.
