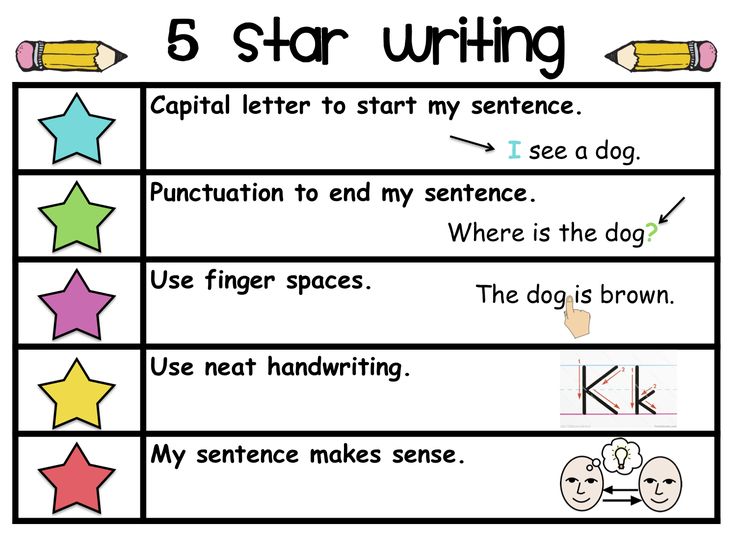
Counting with children
How Children Learn to Count
- Education
- Maths Tips
- 5 and under
Counting is easily taken for granted but there's a lot of fascinating research into how we learn to count - and there's more to it than you may think.
The mathematical brain
It’s first worth considering where our capacity to do mathematics comes from.
Neuropsychologist Brian Butterworth in his book “The Mathematical Brain” suggests we’re born with an innate sense of number hard-wired into our brain and he attributes this to a small region of the brain behind the left ear he calls "the number module". He compares this idea to colour – in the same way we perceive the “greenness” of a leaf we can also perceive the “twoness” or “threeness” of a group of objects.
Take counting. Like times tables and algebra, we tend to think it's something kids have to be taught. Wrong, says Butterworth - it's an instinct. Sure, we have to learn the names and symbols of numbers to develop that instinct, but, because the number module is hardwired into the brain, basic counting comes naturally.
Remote tribes can count even when they have no words for numbers. In maths as in language he believes, "kids start off with little starter kits" And their maths starter kit is the number module.
There are other theories too - such as maths being an extension of our spatial awareness – but there’s something nice in the idea of a “little maths starter kit”.
A Word of warning - All this doesn't mean a child is predestined to be either good at maths or not. Far from it, we’re all born ready to learn maths – and it’s what happens in the first 10 years or so that sets us up.
Counting with toddlers
Research suggest that toddlers - even as young as 12 months - have a sense of how many there are in a set - up to around three objects. This comes from their innate sense of number.
Counting is learned when the toddler starts making the connection between this innate sense of "how many there are" and the language we use to count "one, two, buckle my shoe". This is the first stage in learning maths and it's the building block for many early concepts.
Should parents count with their toddlers? Absolutely, using a variety of real objects. And since counting and language are interlinked reading to your toddlers is equally, if not more, important.
Counting - early learning milestones
Here are some stages of learning to count that you may notice your child going through at ages 3 to 5:
- Recognising how many objects are in a small set without counting. So if you show your child four apples they won't have to count them to tell you there's four.
- Knowing the "number words" from one to ten and their order.
- Know the sequence regardless of which number they start on. So if you say "start counting at four" they will count "four, five .
 ." as opposed to always counting from one.
." as opposed to always counting from one. - Conservation of quantity - This is where children realise that the number of objects in a set stays the same unless any are added or removed. So if they count six cans of beans in a straight line, then you rearrange the beans ( in front of their eyes ) into say two stacks of three - they will realise there's still six without recounting.
- Counting non-visible objects - your child will realise they can count things they can't touch or even see - such as sounds, members of someone else's family, or even ideas.
- Cardinality, not to be confused with carnality - This is knowing that the last number counted is equal to the quantity of the set. If your child counts six oranges 1,2,3,4,5,6 and then you ask "how many oranges are there"? and they count them again then they haven't grasped "cardinality".
Counting on - as a step towards adding
Learning to add comes as an extension of counting. Here are some stages a child goes through to make this connection:
- Counting all - For 3 + 5, children will count "one, two, three" and then "one, two, three, four, five" to establish the quantity of the sets to be added – for example, three fingers on one hand and five fingers on the other.
 The child will then count all the objects "one, two, three, four, five, six, seven, eight"
The child will then count all the objects "one, two, three, four, five, six, seven, eight" - Counting on from the first number - Some children come to realise that it is not necessary to count the first number to add. They can start with three, and then count on another five to get the solution. Using finger counting, the child will no longer count out the first set, but start with the word ‘Three’, and then use a hand to count on the second added: ‘Four, five, six, seven, eight’.
- Counting on from the larger number - It's more efficient when the smaller of the two numbers is counted. The child now selects the biggest number to start with which is "five", and then counts on "six, seven, eight".
- The final stage isn't really counting - it's where learners know their number facts and skip the time-consuming counting altogether.
Number lines are great visual tools for making this connection between "counting on" and addition or subtraction - we use them in Komodo a lot. Here's an earlier blog article all about number lines.
Here's an earlier blog article all about number lines.
Beyond basic counting
Counting is the first mathematical pattern learners encounter. From here they soon begin to count backwards which is a step towards subtraction and they'll also count in twos, fives and tens which are a foundation for multiplication.
The next big step is the idea of place value and counting to base 10. Learners often make this leap simply because it's an obvious and efficient way to count large numbers. In Komodo, we use practice examples like this to help learners make the connection to counting in tens and ones.
It's easy to forget that counting is a key concept in maths with many stages before it's mastered. There's certainly a lot more to it than one, two, three!
I'm Ged, Co-founder of Komodo, ex-maths teacher and dad. If you have any questions please get in touch.
About Komodo - Komodo is a fun and effective way to boost primary maths skills. Designed for 5 to 11 year olds to use in the home, Komodo uses a little and often approach to learning maths (15 minutes, three to five times per week) that fits into the busy routine. Komodo users develop fluency and confidence in maths - without keeping them at the screen for long.
Designed for 5 to 11 year olds to use in the home, Komodo uses a little and often approach to learning maths (15 minutes, three to five times per week) that fits into the busy routine. Komodo users develop fluency and confidence in maths - without keeping them at the screen for long.
Find out more about Komodo and how it helps thousands of children each year do better at maths - you can even try Komodo for free.
Related Posts
Mindset - the path to mastery
People who have a growth mindset believe that they always have the potential to learn and improve. They are more motivated to persevere with difficult tasks, to take risks and to learn from failure.
Top tips to de-stress homework time
Homework can be a trigger for some of the worst fights and arguments that we have with our children. Here are some solutions that can help reduce tensions and get homework done without arguments.
What Children Know and Need to Learn about Counting
Print resource
Print resource or save as PDF
Print feature not currently compatible with Firefox.
DREME TE
Print resource
Print resource or save as PDF
Print feature not currently compatible with Firefox.
Children Develop an Everyday Math
Context and overview
Young children, even infants, develop essentially non-verbal basic concepts of quantity: more/less, order, same, and adding/subtracting. Children learn most of these things on their own, without much adult help. Children often use these concepts in everyday life, for example, to determine who has more or less ice cream. Children’s concepts and procedures are useful under certain conditions but need to be enriched. (Perhaps that’s why number was invented: the shepherd needs to know not only that he has a lot of sheep, but exactly how many.) This is what children know and what they need to learn at roughly ages three, four and five.
Children’s concepts and procedures are useful under certain conditions but need to be enriched. (Perhaps that’s why number was invented: the shepherd needs to know not only that he has a lot of sheep, but exactly how many.) This is what children know and what they need to learn at roughly ages three, four and five.
More/less
Children need to be able to see that there are more objects here than there. They often solve this problem not by counting but by physical appearance. "This flock of geese in the sky must be larger because it covers a greater area than does the other flock." This approach is often adequate but can lead to wrong answers and confusion.
Order
Judgments of more or less are sufficient for many purposes, but sometimes a comparison between more than two things needs to be made. Thus the idea of order, which includes subtle ideas:
- In a group of three objects, the second item is larger than the one preceding it but smaller than the one following it.

- Also, the item that was first can become last under a new order.
Again young children tend to rely too much on appearances to solve the problems.
Same number
The idea of same number evolves, even without adult assistance, through several stages:
- The first step is seeing that two groups identical in shape and arrangement are also the same in number. Thus, if a brown bear and a yellow canary are placed directly below another brown bear and yellow canary, both rows are the same in number (as well as in shape, color, and arrangement).
- The second step is seeing that two groups differing in color or shape can still be the same in number. Thus, if a brown bear and a yellow canary are placed directly under a pink pig and blue heron, both rows are the same in number (and arrangement, although they differ in shape and color).
- The third step is seeing that two groups differing only in arrangement are the same in number.
 Thus, if a brown bear and a yellow canary are not placed directly under a pink pig and blue heron but instead lie elsewhere, both groups are the same in number (although they differ in arrangement, shape and color).
Thus, if a brown bear and a yellow canary are not placed directly under a pink pig and blue heron but instead lie elsewhere, both groups are the same in number (although they differ in arrangement, shape and color). - The fourth is seeing that one group, when rearranged, has the same number as it did before it was moved around. Thus, if the child first sees a brown bear and a yellow canary in one arrangement, which is then transformed, the child realizes that the number did not change from what it was before the rearrangement.
- The fifth is first seeing that two amounts are the same number when they look similar, for example five eggs in a row and five egg cups in a row both have the same number. But then if there is a transformation (for example spreading the eggs apart so that the line of eggs is longer than the line of egg cups), the child has to be able to understand that the eggs and egg cups are the same in number even though the two lines look different.

The idea of adding as resulting in more and subtracting in less
Children learn that:
- When you add something to an existing set, the result is that you have more than you had at first.
- If you start with two groups of the same number, and by magic (while the child is not looking), one set is now more numerous than the other, you must have added to one or subtracted from the other
- You don’t have to count to arrive at these judgments concerning more and concerning addition and subtraction: you can solve the problem by reason alone.
Later instruction needs to build on all of these ideas when written numbers are introduced.
Learning the Counting Words
Context and overview
In everyday life, we use counting words all the time, selecting items from the supermarket (“we need two bananas”) or playing “10, nine, eight, … blast off!” Children love counting as high as they can, like grown-ups. They may even be interested in the name of the highest number. Fluency in the counting words aids later computation.
They may even be interested in the name of the highest number. Fluency in the counting words aids later computation.
Rote memory plus
At first, children memorize the counting words from about one to 10 or so. But their learning doesn’t involve only memory. Children learn some ideas and rules about number too, namely that proper order is essential; numbers are different from letters; and you are not supposed to skip or repeat numbers when you count.
Structure
Later, children pick up the underlying structure of number: ten is the basic unit (20, 30, etc.) and we tack units onto the tens (twenty-one etc.). The rules for saying the English counting words from eleven to nineteen are especially hard to learn because they are poorly designed. Eleven should be "ten-one," just like twenty-one. Fifteen should be "ten-five," like twenty-five. The East Asian languages get this right, but English and many other languages do not. By contrast, English is fairly well designed for the number words beginning with twenty. Each of the tens words resembles a unit word. Forty is like four; eighty like eight, and so on. Fifty comes before sixty. (A fairly minor problem is that twenty should sound more like two and ideally should be “two-ten;” thirty should be “three-ten” and so on). After saying a tens word, the child appends the unit words, one through nine. Learning to count to 20 and beyond is a child's first experience with base-ten ideas. In this case, teaching needs to stress the base-ten pattern underlying the counting numbers: the structure. We need to “instructure” (teach the structure) not “instruct.”
By contrast, English is fairly well designed for the number words beginning with twenty. Each of the tens words resembles a unit word. Forty is like four; eighty like eight, and so on. Fifty comes before sixty. (A fairly minor problem is that twenty should sound more like two and ideally should be “two-ten;” thirty should be “three-ten” and so on). After saying a tens word, the child appends the unit words, one through nine. Learning to count to 20 and beyond is a child's first experience with base-ten ideas. In this case, teaching needs to stress the base-ten pattern underlying the counting numbers: the structure. We need to “instructure” (teach the structure) not “instruct.”
Counting Things: How Many Are There?
Context and overview
Children’s ideas about same, more, less, and order are heavily influenced by perception and by their own imperfect logic (for example, that what looks like more is more). These are good ideas but lack precision, so children need help in taking the next step. The counting words that children learn early on can be used for enumeration; in determining the exact number of a collection, it is the cardinal number that tells how many. Accurate enumeration and understanding of cardinal number are fundamental for all arithmetic (and measurement) and are not as simple as they seem. Rather they involve key mathematical ideas and strategic thinking.
These are good ideas but lack precision, so children need help in taking the next step. The counting words that children learn early on can be used for enumeration; in determining the exact number of a collection, it is the cardinal number that tells how many. Accurate enumeration and understanding of cardinal number are fundamental for all arithmetic (and measurement) and are not as simple as they seem. Rather they involve key mathematical ideas and strategic thinking.
Principles needed to understand enumeration
Enumeration refers to using the counting words to figure out the number of objects. (This includes any object, from imaginary monsters to marbles.) Children must learn to follow several rules and principles to enumerate accurately. This set of rules is fundamental:
- Say number words in their proper order.
- Match one number word with only one thing (one-to-one correspondence between number word and thing).

- Count each thing once and only once.
Given these rules and principles, there are several ways to enumerate with accuracy. Children need to be able to:
- "See” small numbers (up to four or so) without counting. This is subitizing, which can reduce the drudgery of counting.
- Count one object at a time.
- Point at objects.
- Push objects aside to keep track of which ones have been counted.
- Put objects in a line or other orderly arrangement.
- Count on the fingers.
- Group objects into convenient groups that can be subitized or counted.
- Group by 10s.
- Check the answer.
Children need to learn to use these approaches in appropriate situations. For example, if there are only two objects, subitizing may useful, but if there are nine, then pushing objects aside may be indicated.
Understanding cardinality
Children who enumerate accurately also need to understand the result achieved.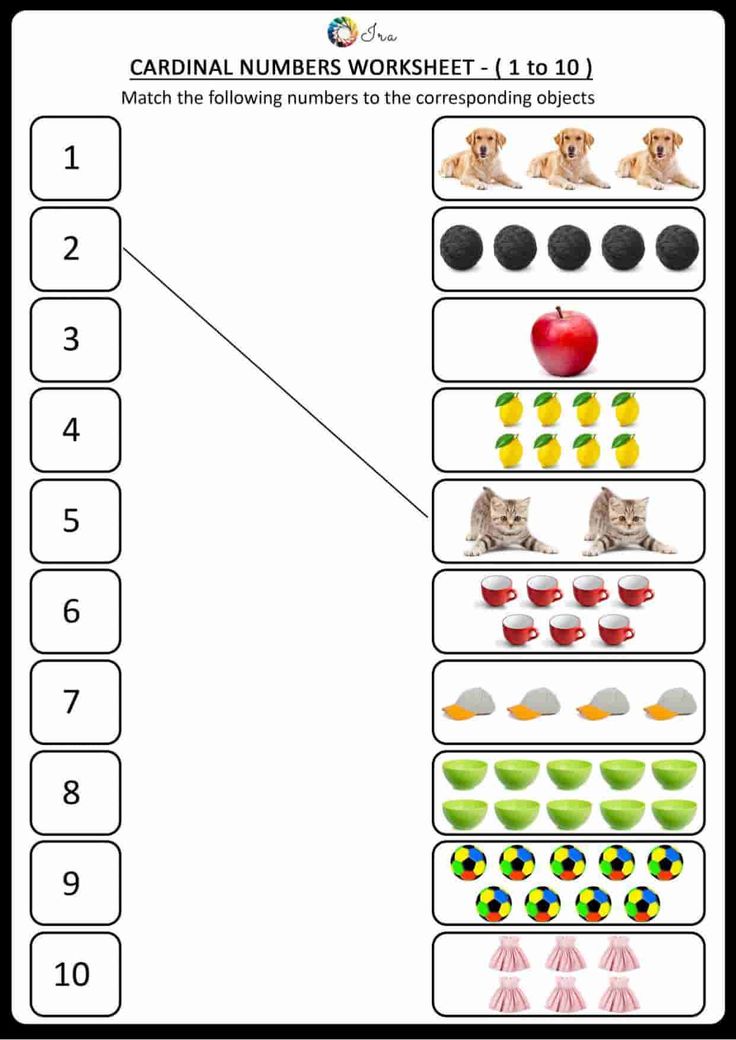 Suppose a child accurately counts five things. Correct enumeration alone does not necessarily mean that the child understands cardinality. Asked how many there are, the child may simply count the objects another time. For that child, answering the question of how many simply activates the counting routine but does not provide an understanding of the result. Children need to learn several things about cardinal number. The core idea is that correct enumeration yields the cardinal value of set. The last number word does not refer to the last object counted but to the set as a whole. When we count, the number one refers to the first object; two refers not to the second object counted but to the two objects in the new group, and so on. Furthermore, once the child has determined that there are five objects in the set, it does not matter if they are hidden, or if the objects are simply rearranged (say from a straight line to a circle). There are still five objects. This is conservation of number.
Suppose a child accurately counts five things. Correct enumeration alone does not necessarily mean that the child understands cardinality. Asked how many there are, the child may simply count the objects another time. For that child, answering the question of how many simply activates the counting routine but does not provide an understanding of the result. Children need to learn several things about cardinal number. The core idea is that correct enumeration yields the cardinal value of set. The last number word does not refer to the last object counted but to the set as a whole. When we count, the number one refers to the first object; two refers not to the second object counted but to the two objects in the new group, and so on. Furthermore, once the child has determined that there are five objects in the set, it does not matter if they are hidden, or if the objects are simply rearranged (say from a straight line to a circle). There are still five objects. This is conservation of number.
Common mistakes or misconceptions
When counting, children often rely too heavily on physical appearance, just as they did in determining more or less. One goal of teaching should be to help children learn that reason must trump appearance. Children need to think abstractly about tangible things. Eventually, they need to embed understanding of cardinal number (for example, the abstract idea that there are five objects here) within the larger system of number, for example, that five comes after four and is half of 10.
Everyday Numerical Addition and Subtraction
Context and overview
Next we need to understand how concepts of more/less, order, same, adding and subtracting without exact number (knowing that adding means making a set larger even if you don't know of the exact number), and enumeration get elaborated to create numerical addition and subtraction. Children learn some of this on their own, but adults can and should help.
Children learn some of this on their own, but adults can and should help.
Understanding addition
These concepts need to be learned to understand addition (subtraction is similar):
- Addition can be thought of in several ways, including combining two sets, increasing the size of one set, and jumping forward on a number line.
- Simple counting is also adding, one at a time.
- The order of addition makes no difference (the commutative property).
- Adding zero changes nothing.
- Different combinations of numbers can yield the same sum.
- Addition is the inverse of subtraction.
Strategies used to add (or subtract)
Children often begin by using concrete objects and fingers to add but gradually learn mental calculation and remember some of the sums.
- Using concrete objects, children may do the following to solve a simple problem like 3 + 2: They may count all ("I have three here and two there and now I push them together and count all to get five") or they may count on from the larger ("I can start with three and then say, four, five.
 ")
") - Approaching the problem mentally, children may solve the problem by derived facts, building on what is known ("I know that two and two is four, so I just add one to get five") and by memory ("I just know it!").
More features of numerical addition and subtraction
- It’s always useful to have backup strategies in case one doesn’t work. For example, if unsure about memory, the child can always count to get the answer.
- It’s important for the child to be able to check the answer.
- It’s important for the child to explain why 3 + 2 gives five as the answer, since proof is a social act requiring language.
- The child needs to learn different strategies for different set sizes. (Counting one by one is good for adding small sets but tedious and inefficient for larger sets.)
- The child should also be able to describe how he got the answer. (Self-awareness is one aspect of metacognition. Of course, remembering what you just did is essential for describing it in words.
 )
) - Language is vital for describing one’s work and thinking, and to convince others; children need to learn mathematical vocabulary.
- The child should be able to apply the math in real situations or stories about real situations (such as word problems).
Number Sense
Context and overview
Children need to develop number sense, a concept that is notoriously difficult to define in a simple and exclusive way. I like to think of it as mathematical street smarts, which can be used in just about any area of number, including those discussed above. Number sense, which helps the child to make sense of the world, has several components, each of which undergoes a process of development.
Thinking instead of calculating
Number sense involves using basic ideas to avoid computational drudgery, as when the child knows that if you add two and three and get five, then you don’t have to calculate to get the answer to three-and-two.
Use what is convenient
Number sense involves breaking numbers into convenient parts that make calculation easier, as when we mentally add 5 + 5 + 1 instead of 5 + 6.
Knowing what’s plausible or impossible
Number sense may involve a “feel” for numbers in the sense of knowing whether certain numbers are plausible answers to certain problems (if you are adding two and three you know that the answer must be higher than three; anything lower is not only implausible but impossible).
Understanding relationships
Number sense involves intuitions about relationships among numbers. (For example, "this is 'way bigger' than that.")
Fluency
Number sense involves fluency with numbers, as when the child knows immediately that eight is bigger than four, or sees that there are three animals without having to count.
Estimation
This involves figuring out the approximate number of a group of objects and is related to the notion of plausible answers.
The Transition to Written, Symbolic Math
Context and overview
Formal, symbolic mathematics can provide children with more powerful tools and ideas than those provided through their informal everyday math. Formal math (and its use of symbols) developed in several cultures and is now virtually universal. Children need to learn it.
Everyday origins and formal math
Children encounter math symbols in everyday life: elevator numbers, bus numbers, television channels and street signs are among the many. Often parents, television, and software activities introduce some simple symbolic math, such as reading the written numbers on the television or on playing cards.
Schools certainly have to teach formal math. But doing so is not easy. Even if they are competent in everyday math, children may have trouble making sense of and connecting their informal knowledge to what is taught in school. Teachers often do not teach symbolism effectively. If children get off on the wrong symbolic foot, the result may be a nasty fall down the educational stairs. So the goal for teachers is to help children, even beginning in preschool, to understand why symbols are used, and to use them in a meaningful way to connect already-known informal mathematics to formal symbolic mathematics. The teacher needs to “mathematize” children’s everyday, personal math; that is, help children connect their informal system with the formal mathematics taught in school. It’s not ill-advised or developmentally inappropriate to introduce symbols to young children, if the activity is motivating and meaningful. On the contrary, it is crucial for the teaching of symbols to begin early on, but again, if and only if it is done in a meaningful way.
If children get off on the wrong symbolic foot, the result may be a nasty fall down the educational stairs. So the goal for teachers is to help children, even beginning in preschool, to understand why symbols are used, and to use them in a meaningful way to connect already-known informal mathematics to formal symbolic mathematics. The teacher needs to “mathematize” children’s everyday, personal math; that is, help children connect their informal system with the formal mathematics taught in school. It’s not ill-advised or developmentally inappropriate to introduce symbols to young children, if the activity is motivating and meaningful. On the contrary, it is crucial for the teaching of symbols to begin early on, but again, if and only if it is done in a meaningful way.
Here are key issues surrounding the introduction of formal math to young children:
Young children have a hard time connecting numerals and the symbols of arithmetic (+ and -) to their own everyday math
They may add well but be confounded by the expression 3 + 2. It is as if the child is living in alternate realities: the everyday world and the “academic” (in the pejorative sense) world. The everyday world makes sense and the world of school does not. You think for yourself in the former and do what you are told in the latter.
It is as if the child is living in alternate realities: the everyday world and the “academic” (in the pejorative sense) world. The everyday world makes sense and the world of school does not. You think for yourself in the former and do what you are told in the latter.
The equals sign (=) is a daunting challenge
The teacher intends to teach the equals sign as "equivalent," and thinks she has, but the child learns it as “makes” (e.g., 3 + 2 makes 5). This is a tale of how child egocentrism meets teacher egocentrism but neither talks with the other.
The solution
We should not avoid teaching symbols but need to introduce them in a meaningful way. This means taking account of what children already know and relating the introduction of symbols to that prior knowledge. It also means motivating the use of symbols. Thus if you want to tell a friend how many dolls you have at home, you need to have counted them with number words (symbols) and then use spoken words (“I have five dolls”), written words (“I have five dolls” written on a piece of paper or a computer screen), or written symbols (5) to communicate the result.
Manipulatives can help
Use of manipulatives can be effective in teaching symbolism and formal math, but they are often utilized badly. The goal is not to have the child play with concrete objects but to use these objects to help the child learn abstract ideas. The goal of manipulatives is to get rid of them by putting them in the child’s head to use as needed in thought. For example, suppose the child learns to represent tens and ones with base-ten blocks. Given the mental addition problem 13 plus 25, the child may understand that each number is composed of 10s (the 10 by 10 squares) and some units (the individual blocks), and that solving the problem involves adding one 10 and two more, which is easy, and then figuring out the number of units. The mental images of the 10s and ones provide the basis for her calculation, part of which may be done by memory (one plus two is three) and part of which may be done by counting on her fingers (five fingers and three more give eight).
Conclusion
The basics of number are interesting and deep. Although young children develop a surprisingly competent everyday mathematics, they have a lot to learn and teachers can help.
Resource Type
Handout
Lesson 3. Preparing for counting for the little ones: tips, activities, games, books
Any child can be taught to count. The only question is how to do it. Despite the fact that counting (including quick calculations) is not a serious difficulty, some children are given it almost in the blink of an eye, while others understand the information with difficulty. Not knowing how to convey seemingly elementary things to the baby, some parents resort to all sorts of tricks, while others give up altogether. In the matter of the full-fledged upbringing and development of the personality, neither one nor the other is completely suitable, and there is only one way out of the situation - to know how, when and what to do. We will talk about this.
We will talk about this.
Contents:
- Peculiarities of learning to count babies
- Initial steps for teaching children to count
- Tasks for the little ones in pictures
- Children's educational games
- Educational literature for children
Peculiarities of teaching kids to count
First of all, it should be said that a child's memory has one special property - selectivity. Therefore, children learn some skills on the fly, without making any effort, and with others, as they say, they have to “tinker”.
It is important to know and always keep in mind that many things cause children to associate with emotional sensations, such as joy, fear or surprise. It is possible to teach a child to count competently and quickly only when this process will also cause him emotional reactions (positive, of course) and interest.
At first, you should make every effort to get your child interested in counting, numbers and numbers. If this is done successfully, even the most fidget will be able to master the skill. A huge plus is that while the development of reading and writing in most cases requires intensive work with notebooks and books, then with the account all this can be relegated to the background. By the way, an interesting fact: thanks to scientific research, it was possible to establish that when studying any language, children remember numerals best of all. But let's continue.
If this is done successfully, even the most fidget will be able to master the skill. A huge plus is that while the development of reading and writing in most cases requires intensive work with notebooks and books, then with the account all this can be relegated to the background. By the way, an interesting fact: thanks to scientific research, it was possible to establish that when studying any language, children remember numerals best of all. But let's continue.
You can start training from the first months of your baby's birth. Of course, this cannot yet be called a full-fledged training - it is rather a preparation. In the period up to about two years, you can play fingers with your child, hum all kinds of songs and counting rhymes, so that the child's consciousness fixes that there are generally such "things" as numbers and numbers. When the baby is two years old, you can move on to more specific methods and techniques. We’ll talk about the methods a little later, but for now, let’s briefly dwell on how to behave with the child in terms of the issue we are considering.
Getting started in teaching children to count
So you've decided to start teaching your child to count. It's time to get started.
First you need to teach the child the simplest number sequence, consisting of five numbers. Remember that almost everything in life can be calculated. Watch a cartoon - count the number of characters on the screen, dress the baby on the street - pay attention to the wardrobe, and tell him that you can only wear one coat on him, that he has two legs, but only one pair of shoes is put on them.
When reading a book, linger on the illustrations longer, count the number of elements depicted in it, animals, little men, houses. When you walk down the street, count the dogs and cats running by, the cars passing by. Doing this every day, and even at every opportunity, your little miracle will definitely learn the order of counting. In addition, auditory and visual memory, as well as attention, will develop.
When a child gets acquainted with numbers and counting, he must understand that he is performing some actions or tasks not because you ask him to, but because it will be useful to him. Show the kid the practical benefits of the ability to count, and then giving out two cookies to everyone at home will not be difficult for him.
Show the kid the practical benefits of the ability to count, and then giving out two cookies to everyone at home will not be difficult for him.
Involve your child in household chores as often as possible. For example, when you are going to have dinner, ask him to serve you a specific number of glasses, plates or cutlery. While cooking, explain that a specific amount of ingredients is required to prepare a particular dish, otherwise the dish will not work.
Dust the bottom shelf - draw a number with a rag and ask the young mathematician to tell you. You can even write an example and then present its solution. Walking around the store will also be a great way to exercise for the baby. Make a grocery list with the baby, clearly pronouncing the amount of everything you need to buy, and bending your fingers on the handles. Let the baby try to remember the information, at least a couple of lines.
Already at the store, remind your tiny assistant that he has to help you and refresh the shopping list in his head. This will activate his brain centers, which means that he will learn to count faster. In addition, you will show the baby that you cannot do without him, and, realizing his importance, he will show more eagerness to help you.
This will activate his brain centers, which means that he will learn to count faster. In addition, you will show the baby that you cannot do without him, and, realizing his importance, he will show more eagerness to help you.
And wind on one important rule: all your actions will not bring any result if you do them randomly. In the matter of training, regularity and perseverance are important. By systematically studying with your child, inventing new forms of elementary everyday learning to count, you will achieve high results.
Now let's get acquainted with more systematic methods of teaching children to count, namely: tasks for the smallest in pictures and children's educational games. Let's start with pictures, because. they are the easiest to work with.
Tasks for the little ones in pictures
Tasks related to pictures are very common and very popular. We offer you a small list of those and brief instructions for use:
- Special cards for learning to count and study mathematical symbols.
 You can find them in any bookstore in a large assortment. You just need to show such cards to the child, explain what is shown on them, and use them to illustrate the performance of mathematical operations.
You can find them in any bookstore in a large assortment. You just need to show such cards to the child, explain what is shown on them, and use them to illustrate the performance of mathematical operations.
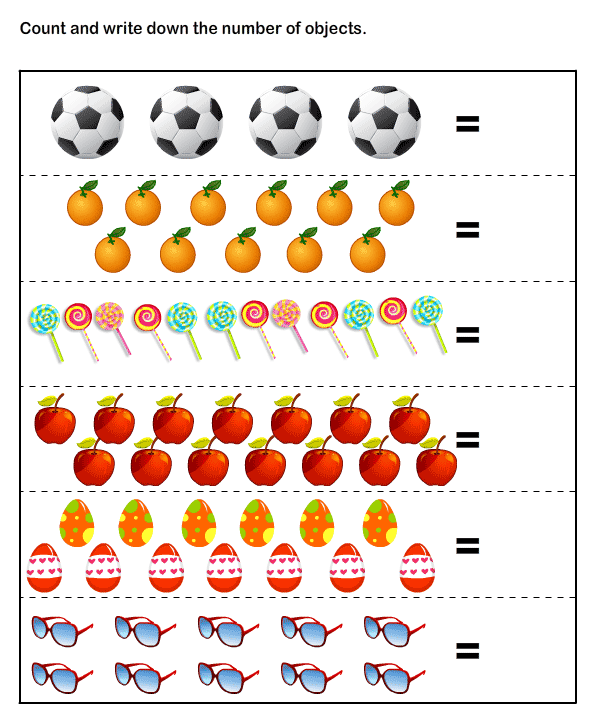
- Pictures with images of various objects. They can not only be counted, but also painted and compiled in the correct sequence. You can buy didactic material in the store, or you can make it yourself (we recommend the first option).
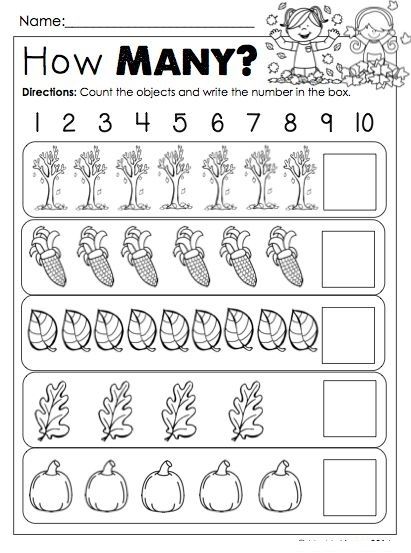
- Images that involve matching pictures and numbers. It is very simple to use: the kid looks at the picture, determines the number of objects and draws a line with a pencil to the corresponding number. Collections of similar images are also available in bookstores.
- Pictures of different objects and you want to determine the number (little or many), size (small or large) and height (high or low).
- Images with specific tasks, such as walking through a maze, finding the same items, finding differences, etc.

Toddlers are very fond of tasks with pictures, because they are funny, cheerful and colorful. But for you, as teachers, it is more important that they clearly show the child what is what, thanks to which he easily remembers the material, understands the meaning of his actions and can explain it to you. Be sure that the kid will look forward to each new lesson with pictures.
Children's educational games
We will not surprise you if we say that the best form of learning for children is the form of play. If you build the learning process based on the game, the child will be involved and interested in it. And even numbers that may seem boring will delight and bring pleasure. But we want to introduce you not to simple games, but to interactive ones, i.e. with those that you can safely download and install on your computer or tablet, or simply open on the Internet.
1
The game "Masha and the Bear answer questions"
A very exciting and colorful game where the kid will have to be smart and use the ability to add and subtract. The bottom line is that a small player must help Masha give the correct answers to mathematical questions. By doing this, he will help her get to visit her grandparents. If the child answers incorrectly, the bear sits on a stump, preventing Masha from passing. You need to give as many correct answers as possible.
The bottom line is that a small player must help Masha give the correct answers to mathematical questions. By doing this, he will help her get to visit her grandparents. If the child answers incorrectly, the bear sits on a stump, preventing Masha from passing. You need to give as many correct answers as possible.
2
The game "Math with Luntik"
Luntik is one of the favorite cartoon characters of children. If your little one plays this game, he will quickly learn to add numbers up to ten. With the correct answer, Luntik rejoices, and with the wrong answer, he is sad. Tasks in the game like this: Luntik writes an example with a plus sign, and the player must find the correct answer (several options are offered). The game is accompanied by pleasant music that helps the baby to concentrate.
3
Bouquet game
The meaning of the game is as follows: flowers bloom in the garden, which you want to put in vases. The player is given three vases with different numbers. In each vase you need to put the appropriate number of flowers. So, while happily manipulating virtual objects, your child will quickly learn to identify numbers and correlate them with the number of objects.
In each vase you need to put the appropriate number of flowers. So, while happily manipulating virtual objects, your child will quickly learn to identify numbers and correlate them with the number of objects.
4
Piggy treats game
Another wonderful toy, the main characters of which are Piggy and his friends. The task of the game is to properly distribute treats to guests. For example, you need to help Piggy to share the nuts for everyone. There is a number next to the plate of each guest, and the correct number of nuts should be put on each plate. The interface of the game is designed so that the child can easily learn to count and memorize the images of numbers.
5
Animal Count Game
This game is suitable for toddlers who can count to five. Your child is presented with four pictures and one number, and he must find the picture, the number of animals in which corresponds to this number.
By and large, you can find a lot of similar games. All that is required for this is to type the desired request on the Internet. But games, of course, should not be limited, because they should be only an accompanying element of classes. In addition to them, we strongly recommend that you do not neglect children's poems and rhymes that activate children's thinking and make it more flexible. Be sure to connect the numbers when your beloved gold draws, paints, sculpts from plasticine or cuts something. And don't forget about children's books that contain counting tasks, drawings of numbers, simple examples, and other attributes of mathematics.
All that is required for this is to type the desired request on the Internet. But games, of course, should not be limited, because they should be only an accompanying element of classes. In addition to them, we strongly recommend that you do not neglect children's poems and rhymes that activate children's thinking and make it more flexible. Be sure to connect the numbers when your beloved gold draws, paints, sculpts from plasticine or cuts something. And don't forget about children's books that contain counting tasks, drawings of numbers, simple examples, and other attributes of mathematics.
Speaking of literature, at the end of the lesson we want to present some good teaching aids that will help you learn many interesting features of the process of teaching children to count and build the process even more effectively.
Educational literature for children
A variety of manuals are used today to teach kids to count. As a rule, they describe all kinds of techniques that develop mathematical abilities, memory and attention, logic and thinking in general, and also allow children to instill a love of mathematics.
Given that there are a lot of such manuals today, you need to find one that will be of interest to you and your little one. Therefore, you need to be prepared to spend some time studying thematic literature (if, of course, you have a desire).
We offer you a small list of excellent books that you can choose without fear that time will be wasted:
- Alla Kharchenko “Mathematics for kids. I count to 10"
- Daria Denisova "Mathematics for kids"
- Svetlana Gavrina "Mathematics for the little ones"
- Alexander Zvonkin "Kids and Mathematics"
- Elena Kolesnikova "Mathematics for children 3-4 years old"
- Elena Bakhtina "Mathematics for kids from 2 to 5"
In the fifth lesson you will learn a little more about how to work with preschoolers, how to introduce the child to the world of numbers and the composition of the number, and some simple tasks that can be given to children to solve.
Test your knowledge
If you would like to test your knowledge on the topic of this lesson, you can take a short test consisting of several questions. Only 1 option can be correct for each question. After you select one of the options, the system automatically moves on to the next question. The points you receive are affected by the correctness of your answers and the time spent on passing. Please note that the questions are different each time, and the options are shuffled.
Only 1 option can be correct for each question. After you select one of the options, the system automatically moves on to the next question. The points you receive are affected by the correctness of your answers and the time spent on passing. Please note that the questions are different each time, and the options are shuffled.
Statistics Full screen
Kirill
← 2 Advantages and disadvantages 4 Learning numbers →
Teaching children to count
Along with such skills as reading and writing, the ability to count is very important. Despite this, many parents prefer to focus their efforts on teaching their child other skills. However, we do not advise you to delay this, because early learning to count will serve your child as an excellent service in the future.
In favor of this, we will give several arguments, and at the same time answer the question: why does a child need to be able to count at all?
Contents:
- Why is it important to teach your child to count
- Features of teaching children to count
- Stages of teaching children to count according to A.
 M. Leushina
M. Leushina - When to start teaching children to count. Initial teaching methods
- How to explain to a baby the concept of the number
- Quotes of famous people about the ability to count
Why it is important to teach a child to count
One can talk endlessly about the benefits of reading, but we will only point out the main reasons and benefits of teaching a child to count:
- Mathematical calculations are considered one of the highest functions of the human brain. Only humans can count. Mastering counting skills has a beneficial effect on brain development.
- Mastering counting skills develops mathematical thinking and thinking in general.
- Learning to count instills an interest in mathematics, which means that from an early age you can prepare a child to study in a mathematical class and participate in arithmetic Olympiads (unless, of course, interest is maintained over time and does not disappear).

- Mastering counting skills contributes to the development of memory, logic and attention.
- The ability to count is always useful in life, because many professions, and life situations often require a person to be able to count.
This list can be continued, but the bottom line is that the development of numeracy is part of the full and harmonious development of the child's personality. It is extremely important that parents develop their child in different directions during upbringing, and counting is one of those.
But how do you start developing your baby's first counting skills? Are there any rules to follow? We will answer these questions in the next section.
Features of teaching children to count
Unfortunately, there is no consensus on teaching children the science of counting. For example, Anna Mikhailovna Leushina, a well-known teacher, doctor of pedagogical sciences and a recognized specialist in preschool education, believed that one should not rush to learn counting at all, and one should learn to count only after mastering the simplest operations on sets.
The fact is that the account is such an activity that has its own specific features, namely: the goal, means, methods of implementation and results, expressed in the form of a final number as an indicator of the power of the set.
The meaning of counting as an activity is to establish a one-to-one effect between the elements of a certain set and the numbers of the natural series as a standard set of numbers, where all these numbers reflect a certain class of sets.
A huge number of psychological and pedagogical research, carried out at one time by such specialists as V. V. Danilova, G. S. Kostyuk, A. M. Leushina and others, showed that children begin to master the account gradually, and this process itself passes a number of stages.
Stages of teaching children to count according to AM Leushina
It is always necessary to teach children to count from practical operations with sets, their splitting into components and comparison of adjacent sets. Account activity can be divided into the account stage and the total stage. Based on this, there is a correlated account and a final account. Correlated account, i.e. the process of counting, expressed in naming a number, is much easier for children to master, and it is more difficult to master the result of counting.
Account activity can be divided into the account stage and the total stage. Based on this, there is a correlated account and a final account. Correlated account, i.e. the process of counting, expressed in naming a number, is much easier for children to master, and it is more difficult to master the result of counting.
Thus, AM Leushina identified six basic stages in the development of counting skills in children. The first two stages are considered preparatory. Passing them, children carry out operations with sets without using numbers. The quantity is estimated by means of the words “none”, “one”, “many”, as well as “more”, “less” and “equally”. In other words, the first two stages are pre-numeric stages, and the other four are numeric. Let's talk in more detail about each of the stages.
First stage
Typically, the first stage corresponds to the second and third years of a child's life.
The purpose of this step is to familiarize yourself with the structure of the set.
The main methods of learning are the selection of components in the set, as well as the compilation of a set of elements. At this stage, kids compare one and many.
The second stage
The second stage refers to the same age period. But the difference with the first is that kids learn to count by going through special math classes.
The purpose of the stage is to teach the child to compare element by element adjacent sets - sets that differ in the number of components by one unit.
The main methods of learning are comparison, application and overlay. Thanks to them, the child masters the skill of establishing equality from inequality by adding or eliminating one element.
The third stage
The third stage corresponds to the fifth year of life.
The goal is to familiarize the child with the formation of numbers.
At this stage, children learn to compare adjacent sets and establish equalities, as a result of which they master the result of counting, indicated by a number.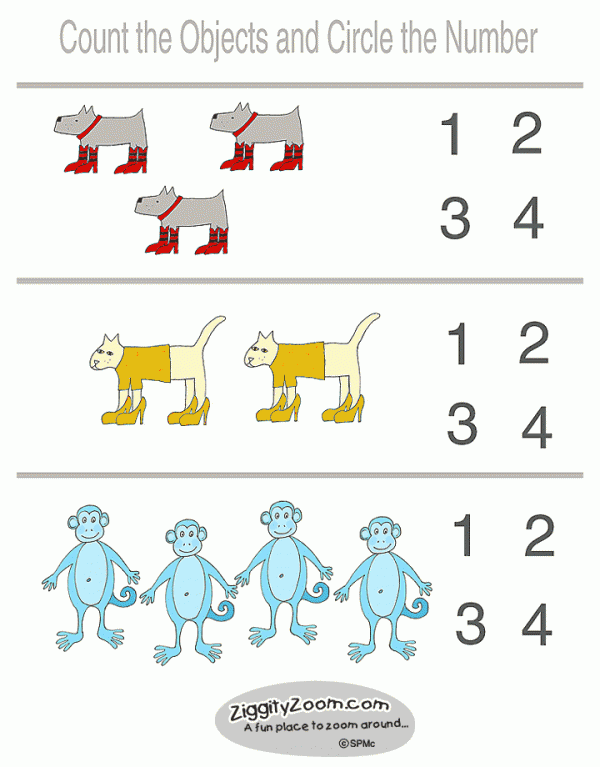 It turns out that at first the baby learns to count, and then he understands its result - the number.
It turns out that at first the baby learns to count, and then he understands its result - the number.
Fourth stage
The fourth stage is realized in the sixth year of life.
The goal is to introduce the child to the ratio of adjacent numbers of the natural series. As a result, he comes to understand the basic principle, according to which each number has its place, each next number is more than the previous one by one, and each previous one is one less than the next.
Fifth stage
The fifth stage corresponds to the seventh year of life.
The goal is to explain to the child the group count (counts in groups of 2, 3 or 5). As a result, the child begins to master the decimal system of calculus.
In most cases, at the fifth stage, preschoolers finish learning to count.
Sixth stage
The sixth stage also corresponds to the seventh year of life.
Aimed at improving children's skills in decimal calculus. The child learns how the numbers of the second ten are formed, begins to understand how any number is formed, that there are ten units in one ten, that when ten units are added to one ten, two tens are obtained, etc.
These are the main stages of teaching children to count, established by AM Letushina. If you take this information into account and build the process of teaching your child to count, guided by it, the material will be absorbed much more efficiently, and the results will please you and your child.
Now it is worth talking about when you can directly start practical actions, and what methods are most effective at each age.
When to start teaching children to count. Initial teaching methods
As it has already become clear, it is better not to hurry with learning to count, but it is still necessary to prepare the baby little by little to master the count. Here's a system you can follow:
- While the baby is not a year old. The child's brain is not yet ready for the full perception of information, so there is no point in teaching counting. However, you can start preparing it.
- Period from 1 to 3 years. Introduce the little one to what is little and what is much.
 For example, one toy is in the pen, but there are many toys in the box. Use dolls, nesting dolls, cars and other toys that fit easily in a child's hand. It is not necessary to conduct classes for a long time, otherwise the child will quickly get tired. As soon as you see that interest is gone, take up another activity.
For example, one toy is in the pen, but there are many toys in the box. Use dolls, nesting dolls, cars and other toys that fit easily in a child's hand. It is not necessary to conduct classes for a long time, otherwise the child will quickly get tired. As soon as you see that interest is gone, take up another activity. - Period 3 to 4 years. Go to comparison. In the process, you can use absolutely everything that can be compared. Offer your baby objects of different sizes and in different quantities.
- Period 4 to 5 years. Start counting a little. It is convenient to start with picture cards so that the child learns the relationship between the concept of the number and the number of objects. Provide as much visual information as possible - show cards with the number of objects and name their number. In addition, introduce the child to the numbers, again showing the cards. Bending and unbending your fingers, learn to count to ten.
 Use "Stoschet Zaytsev" in your work. Explain the numbers figuratively: the number "1" looks like a thin man, the number "2" looks like a swan, etc.
Use "Stoschet Zaytsev" in your work. Explain the numbers figuratively: the number "1" looks like a thin man, the number "2" looks like a swan, etc. - Period 5 to 6 years. At this stage, move on to solving simple problems. Strive to convey to the child information about the quantitative meaning of the number, i.e. three is three ones, four is four ones, and so on. Buy a number line from a bookstore and show which numbers are bigger, which ones are smaller, which ones are ahead, which ones are further, etc. Be sure to spend time solving problems like “How many bears?”, “Which is more: cubes or balls?” etc.
Remember that you need to teach counting only gradually and systematically. In future lessons, we will talk about the methods of teaching counting in more detail. In the meantime, our task is to understand the principle of future actions.
And summing up the introductory lesson, we want to tell you about how you can explain to a child what a number is.
How to explain the concept of number to a child
The concept of number can safely be called the basis of counting and mathematics. But it, like any concept from the field of mathematics in general, is an abstract category. For this reason, difficulties often arise when explaining to a child the essence of a number.
To make this easier, here are some good tricks:
- Read nursery rhymes (some can be memorized). The counters are most effective - they can become the basis for understanding the concept of number. The counting rhymes are extremely simple: “One, two, three - look at your mother”, “One, two - we go for firewood”, etc. Even before the moment when the child notifies you that he has four cubes, he will already be able to pronounce counting rhymes, thereby studying the pronunciation of numbers and recognizing their features.
- Compare pictures where there are similarities and differences in terms of the number of objects depicted in them.
 Ask the child what is the difference between the pictures, and also give him the task to independently draw on paper a different number of objects - houses, animals, trees, people, etc.
Ask the child what is the difference between the pictures, and also give him the task to independently draw on paper a different number of objects - houses, animals, trees, people, etc. - Use counting sticks. Ask the little one to put three sticks on the table, and then ask how many sticks are in front of him. You can spread the sticks on different sides of the table and ask how many sticks are on which side. Do as many manipulations with these sticks as possible.
- Everywhere and always count: climbing stairs, eating porridge with spoons, collecting a pyramid of cubes, bending and unbending fingers on arms and legs, etc. Try to draw your child's attention to what is happening around, wherever you are and whatever you do. And always be interested in how much of this or that he sees next to him.
- Even at the smallest age, one can not only name numbers, but introduce elements of mathematical operations. For example, like this: “There are five benches in the yard, you and I have already sat on three.
 How many benches have we not sat on yet?”, or “Look, there are only ten steps, here we have passed one. How many steps are left”, etc. Let the baby still not understand what you want from him, but he will subconsciously perceive the incoming information, which will certainly manifest itself in the future.
How many benches have we not sat on yet?”, or “Look, there are only ten steps, here we have passed one. How many steps are left”, etc. Let the baby still not understand what you want from him, but he will subconsciously perceive the incoming information, which will certainly manifest itself in the future.
Understand the most important thing for yourself: learning to count should be fun for the child, and he should enjoy it. Therefore, in no case do not force the child to study the account and numbers. It is better to turn all activities into a game. It is also very important to show the growing little man why you need to be able to count and what is the use of it. However, we will talk about all this later.
In the second lesson, you will learn the most common approaches to learning to count, some exercises and the secrets of successful learning.
Lesson 1. The most common methods of teaching children to count
The ability to count makes the life of even an adult much easier, because it allows you to be more efficient at work, save time, and achieve better results. As for children, oral counting skills are needed so that they can more successfully master the exact sciences when they study at school, and also competently operate with objects of the world around them.
As for children, oral counting skills are needed so that they can more successfully master the exact sciences when they study at school, and also competently operate with objects of the world around them.
As it has already become clear, it is necessary to think about how to teach your precious child to count long before the moment when it is time to go to the first grade. It is precisely because of the need for appropriate teaching methods and the relevance of this issue in general that not only specialists in preschool education, but also parents themselves, for many years, learning from their mistakes, came up with various ways to teach children to count.
Lesson 2. Advantages and disadvantages of the main methods of teaching children to count
In the second lesson we talked about the most common methods of teaching children to count. In the same lesson, we will analyze in more detail the methods of Nikolai Zaitsev and Glen Doman we mentioned earlier, talk more specifically about counting on fingers and mental counting, and also point out the pros and cons of all these methods.
We have already understood that the ability to count, together with the ability to read and write, belongs to the first step in home schooling. It is likely that you have already tried your hand at teaching a child to count, and most likely noticed that success can be achieved even without special didactic tools and pedagogical skills.
Lesson 3. Preparing for counting for the little ones: tips, activities, games, books
Any child can be taught to count. The only question is how to do it. Despite the fact that counting (including quick calculations) is not a serious difficulty, some children are given it almost in the blink of an eye, while others understand the information with difficulty. Not knowing how to convey seemingly elementary things to the baby, some parents resort to all sorts of tricks, while others give up altogether. In the matter of the full-fledged upbringing and development of the personality, neither one nor the other is completely suitable, and there is only one way out of the situation - to know how, when and what to do. We will talk about this.
We will talk about this.
Lesson 4. Studying numbers
Any teaching of counting and numbers should always begin with the assimilation of elementary quantitative concepts, such as "a lot", "little", "more", "less", "equally", etc. . And children easily understand them even at a toddler age. Your main parental task is simply to help them with this. The skills of quantitative comparison can be formed in the process of everyday life. So, together with the baby, you can compare the number of sweets or sandwiches, apartments on the playgrounds and steps on the stairs, pigtails and bows for girls, etc. However, it is not necessary to take on large groups of objects at once, because everything should start small.
After mastering quantitative concepts, it's time for the baby to get acquainted with the world of numbers. As you already know, this should happen in an interesting and exciting way for the child, for which the methods we discussed in the first lessons should be applied.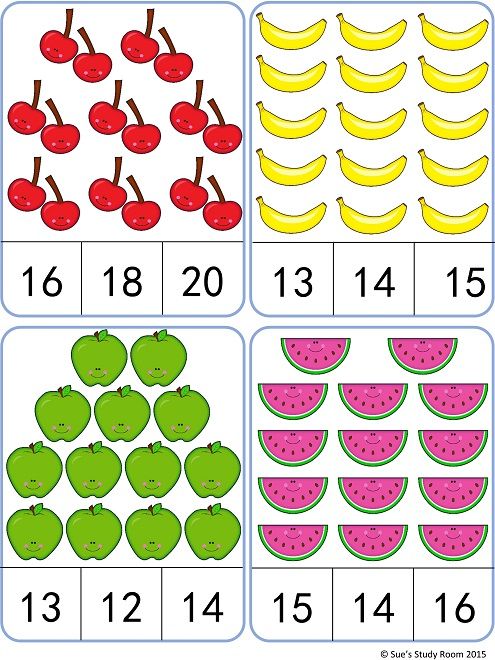
Lesson 5. Principles of learning to count. Counting up to 10, up to 20 and up to 100. Counting in a column
As soon as children reach the age of 2-3 years, it is time to deal with counting more seriously with them than just telling them what is "little" and "a lot" and how much will be "2 + 2". This age period is characterized by maximum cognitive activity, and cognitive abilities reach their peak. That is why the children themselves are distinguished by curiosity and the desire to learn something that they did not know how to do before. As a result, the incoming information falls on fertile ground, and then begins to be actively used by children in their interaction with surrounding objects and people.
But when teaching a child to count, one should always keep in mind that some data can be somewhat problematic to assimilate. The child may, for example, miss some numbers from the number series or completely change their order. The reason for this is the selectivity of children's memory - for the most part, it lingers in what caused an emotional response in the mind, in particular, interest. Therefore, training should be built with a foundation on several fundamental principles that you definitely need to get acquainted with.
Therefore, training should be built with a foundation on several fundamental principles that you definitely need to get acquainted with.
Lesson 6. Studying the multiplication table
The numbers are studied, the basic mathematical concepts are mastered, the child freely counts up to a hundred, adds and subtracts - all this suggests that it is time to start studying the multiplication table.
The multiplication table can be given to a future student more difficult than the basics of mathematics, and as a parent interested in the development of his child, you are obliged to support him in this matter. As before, you will need a fair amount of patience and perseverance.
Lesson 7. Eliminating problems with mathematics
In this lesson, we will try to consider not so much the problems with the technical side of mastering mathematical knowledge, but the problems of a more global, one might say, psychological nature.
There are several reasons for this. You will learn about them in this lesson.
Lesson 8. How to make a child fall in love with mathematics
You can endlessly engage in mathematics with your child, learn the multiplication table, solve hundreds of examples, but still you can’t make him begin to have warm feelings for this subject. For many children, mathematics is not only difficult, but also a very boring subject. As a result, numbers, examples and tasks are not interesting for children, and are given to them with great difficulty. Many parents in such cases come to the conclusion that their children have a humanitarian mindset, but not always the reason lies in the lack of abilities for technical sciences and all kinds of calculations.
As you know, attitude towards something automatically affects the desire to deal with it. Remember yourself: how often does it happen that you don’t like something, as a result of which, even if you have to interact with it (do some things, solve some tasks, communicate with specific people), you show absolutely no enthusiasm. The situation is exactly the same in the context of our topic. It is likely that the child's failures in mathematics are due to the fact that he simply does not like it. And in order to remedy the situation, you need to know the ways by which you can instill in your child a love of mathematics. Remember that, first of all, your task, as a parent-teacher, is to convey to the mind of the child that mathematics can be both interesting and useful, and in general, you can enjoy it.
The situation is exactly the same in the context of our topic. It is likely that the child's failures in mathematics are due to the fact that he simply does not like it. And in order to remedy the situation, you need to know the ways by which you can instill in your child a love of mathematics. Remember that, first of all, your task, as a parent-teacher, is to convey to the mind of the child that mathematics can be both interesting and useful, and in general, you can enjoy it.
Lesson 9. Basic math tricks
Having covered the most important questions and the most difficult moments in the process of teaching children to count, now we can afford to relax a little. Today we will get acquainted with ten simple mathematical tricks, which, firstly, will help your child realize that mathematics is simple and interesting, and secondly, will teach him to enjoy computing. However, it will be useful for you, as parents, to brush up on arithmetic knowledge and, perhaps, discover something new for yourself.
The following math tricks will improve your precious child's skills and speed up their mental math skills.
- Firstly, the presented section of our course is devoted to teaching counting to children, mainly preschool and primary school age.
- Secondly, many technical problems have already been discussed in the first lessons of this section, and we have given a lot of information on how to avoid the most common mistakes that cause technical problems.
- Thirdly, the psychological aspect is important because already at a young age it is possible to trace whether the child has difficulties in mastering the material, whether he has a craving for mathematical knowledge, what he gravitates more to - to the humanities or the exact sciences.
Next, we suggest taking a break and getting a charge of additional motivation for taking the course.
Quotes from famous people about numeracy0005 quotes from famous people
about numeracy:Everything that is known has a number, because it is impossible to understand anything, or to know without it.

Pythagoras
A purely mathematical mind will work correctly only if all definitions and beginnings are known to it in advance, otherwise it gets confused and becomes unbearable, because it works correctly only on the basis of clearly formulated beginnings.
Blaise Pascal
Mathematics contains not only truth, but also the highest beauty - cold and austere beauty, like the beauty of a sculpture.
Bertrand Russell
The Lord created whole numbers, the rest is the work of man.
Leopold Kronecker
Mathematics is the queen of sciences.
Carl Friedrich Gauss
The Book of Nature is written in the language of mathematics.
Galileo Galilei
Mathematics is proving the most obvious things in the least obvious way.