Ordinal math definition
What are Ordinal Numbers? Definition, List, Examples, Facts
What are Ordinal Numbers?
Numbers that are used to represent the rank or position of an object or a person are known as ordinal numbers. They are also referred to as positioning or ranking numbers.The sequence of ordinal numbers vary on the parameters that are based on the positions that are defined, such as weight, height, marks, size, etc. Such numbers are also known as ordinals.
Related Games
How to Write Ordinal Numbers?
Ordinal numbers or ordinals are written using numerals as prefixes and adjectives as suffixes.
For example, 1st, 2nd, 3rd, 4th, 5th, 6th, 7th, 8th and so on. We can easily identify an ordinal number: it talks about positioning.
So, if we were to say, “Bring me the bottle of jam that is lying on the 4th shelf.”, one would know that the ordinal number here is 4, which informs us about the position of the jam bottle.
The above picture shows different floors of a building. Here, we can use ordinal numbers to define the position of the floors.
The numbers 1st (first), 2nd (second), 3rd (third), 4th (fourth), 5th (fifth), 6th (sixth), 7th (seventh), 8th (eighth), 9th (ninth) and 10th (tenth) tell us about the positions of various floors in the building. Therefore, all of them are the ordinal numbers.
Related Worksheets
Applications of Ordinal Numbers
Ordinal numbers are a great way to talk about the order of something. For example, the order of dates. These numbers are only used when data is provided and the data is to be arranged in order.
For example: Someone who has performed well throughout the year may get the chance to be valedictorian. They would be first in line. But someone who performed well, but was unable to score as much as the person before in various tests and exams, may be second in line to be valedictorian. The person who has not performed well at all, has the least amount of chance.
The person who has not performed well at all, has the least amount of chance.
The picture given below shows some athletes competing in a 500-m race. We can also use ordinal numbers to define their positions in order to see who the winner and runners-up of the race are.
Other examples of ordinal numbers are as follows:
- Jennifer always ranks 2nd in the class.
Here 2nd is the ordinal number that tells you about the position that Jennifer has secured.
- Jane is standing at the 5th place in the queue.
Hereby the ordinal number is 5th, we understand Jane’s position in the queue.
- Jenny came 3rd in the race.
Here, 3rd is the ordinal number which tells you about the place that Jenny has secured in the race.
- The 10th table is reserved.
Here, the ordinal number 10th refers to the number of table reservations made.
Ordinal Numbers 1
– 50 listOrdinal Numbers 51
–100 listOrdinal Numbers v.
 Cardinal Numbers
Cardinal NumbersThe type of numbers that are used for counting the number of objects or persons are known as cardinal numbers. This type of numbers are used for representing the cardinality of the number of elements in a set.
Cardinality means to know about the number of elements in a set.
Cardinal numbers can be the natural numbers that we use while we are counting like one, two, three, four, five and so on.
On the other hand, ordinal numbers are used to determine the rank or position of any object or person. We write ordinal numbers using numbers as prefixes and adjectives as suffixes.
Let us understand the difference with the help of an example.
Some students were asked to collect marbles.
Tom collected 1, Jane collected 2, and Clove collected 3 marbles.
Here the numbers 1, 2, 3 are cardinal numbers as they represent the quantity of marbles.
Now, the one who scores maximum wins. So, Clove stands 1st, Jane stands 2nd and Tom stands 3rd.
Here the numbers 1st, 2nd and 3rd are ordinal numbers as they represent the position of the students.
Ordinal Numbers v. Nominal Numbers
A set of numbers that are used for labeling certain items or places so that they can be identified easily are known as nominal numbers. Whenever we have to identify an object uniquely, we use nominal numbers. These numbers are not of much use because they are just going to give information about location and not about its quantity, quality, etc. Nominal numbers can be used as area codes, on number plates of vehicles, etc. Operations such as addition, subtraction, multiplication and division are meaningless on nominal numbers.
For example: In a phone number like 202 588-6500, the number is a nominal number. Even if we apply an operation, it will not give us anything meaningful.
On the order hand, the ordinal numbers tell us about the rank or position of any object or person.
For example: Sophia lives in the 34th house on San Pablo Avenue, California.
Fun Fact!
11, 12 and 13 are the only numbers to use a suffix ‘–th’ but all other numbers ending with 1 use ‘–st’, those ending with 2 use ‘–nd’ and those ending with 3 use ‘–rd’.
Solved Examples On Ordinal Numbers
Example 1: Which English alphabet is 12th from the beginning?
Solution: The alphabet that is 12th from the beginning is L.
Example 2: Kim, Kethy, Kiah and Kaina are sitting in the line in alphabetical order. What is the position of Kiah from the beginning?
Solution: According to alphabetical order, the order in which they’re sitting would be: Kaina, Kethy, Kiah, Kim. So, Kiah is at the 3rd position.
Example 3. Christmas lies on the _____ of December.
Solution: Christmas lies on the 25th of December.
Practice Problems On Ordinal Numbers
1
Which one of the following denotes an ordinal number?
The vehicle number of Sarah is KL23AB89.
There are 9 apples on the tree.
Catheline came 4th in the drawing competition.
None of these
Correct answer is: Catheline came 4th in the drawing competition.
In the option C, the number 4th is telling about the position of Catheline in the drawing competition.
2
How do you write 51 in ordinal numbers?
51
51st
51th
51rd
Correct answer is: 51st
The ordinal number for 51 for 51st.
3
In the word, “COMPENSATION”, which are the fourth and tenth letters?
M and O
M and N
P and I
E and O
Correct answer is: P and I
The fourth letter is P and the tenth letter is I.
Frequently Asked Questions On Ordinal Numbers
Is 0 an ordinal number?
No, we cannot write 0 as an ordinal number.
What are exceptional ordinal numbers?
Exceptional ordinal numbers are the ordinal numbers that do not end with -th. For example: 1st (first), 2nd (second), 3rd (third), etc.
For example: 1st (first), 2nd (second), 3rd (third), etc.
Who invented ordinal numbers?
Ordinal numbers were invented by Georg Cantor in 1883.
Ordinal Numbers - Meaning, Examples
Ordinal numbers are the numbers that talk about the position of objects. For example, 'The cookies are kept in the 3rd drawer from the top', 'The orange dress is the 7th one from the right', 'The soccer ball is kept in the 3rd carton from the left'. All these sentences have one thing in common - they talk about the positions of the objects. This is the main element in the discussion of ordinal numbers.
| 1. | What are Ordinal Numbers? |
| 2. | Difference Between Cardinal and Ordinal Numbers |
| 3. | List of Ordinal Numbers from 1 to 100 |
| 4. | FAQs on Ordinal Numbers |
What are Ordinal Numbers?
An ordinal number is a number that indicates the position or order of something in relation to other numbers, like, first, second, third, and so on. This order or sequence may be according to the size, importance, or any chronology. Let us understand the ordinal numbers with an example. Ten students participated in a contest. Out of them, the top winners were given medals and were ranked as 1st, 2nd, and 3rd. In this case, the positions: 1st, 2nd, and 3rd are ordinal numbers.
This order or sequence may be according to the size, importance, or any chronology. Let us understand the ordinal numbers with an example. Ten students participated in a contest. Out of them, the top winners were given medals and were ranked as 1st, 2nd, and 3rd. In this case, the positions: 1st, 2nd, and 3rd are ordinal numbers.
Difference Between Cardinal and Ordinal Numbers
A cardinal number is a number that denotes the count of any object. Any natural number such as 1, 2, 3, etc., is referred to as a cardinal number, whereas, an ordinal number is a number that denotes the position or place of an object. For example, 1st, 2nd, 3rd, 4th, 5th, etc. Now, if we say, 'There are 3 ants and 5 bears'. This is an example of cardinal numbers. However, if we say, 'The position of the runners in the running event is first, second, third, and so on', this represents ordinal numbers. Observe the table given below to note the difference between cardinal numbers and ordinal numbers.
Observe the table given below to note the difference between cardinal numbers and ordinal numbers.
List of Ordinal Numbers from 1 to 100
The list of ordinal numbers from 1 to 100 can be learned easily and is quite helpful for specifying the order of any given object. You can use the combinations from this list to find out the ordinal numbers from 100 onward. Observe the table given below in order to understand how ordinal numbers are written. You might be able to pick up a pattern after referring to the first twenty ordinal numbers.
| 1st: First | 21st: Twenty-First | 41st: Forty-First | 61th: Sixty-First | 81st: Eighty-First |
| 2nd: Second | 22nd: Twenty-Second | 42nd: Forty-Second | 62nd: Sixty-Second | 82nd: Eighty-Second |
| 3rd: Third | 23rd: Twenty-Third | 43rd: Forty-Third | 63rd: Sixty-Third | 83rd: Eighty-Third |
| 4th: Fourth | 24th: Twenty-Fourth | 44th: Forty-Fourth | 64th: Sixty-Fourth | 84th: Eighty-Fourth |
| 5th: Fifth | 25th: Twenty-Fifth | 45th: Forty-Fifth | 65th: Sixty-Fifth | 85th: Eighty-Fifth |
| 6th: Sixth | 26th: Twenty-Sixth | 46th: Forty-Sixth | 66th: Sixty-Sixth | 86th: Eighty-Sixth |
| 7th: Seventh | 27th: Twenty-Seventh | 47th: Forty-Seventh | 67th: Sixty-Seventh | 87th: Eighty-Seventh |
| 8th: Eighth | 28th: Twenty-Eighth | 48th: Forty-Eighth | 68th: Sixty-Eighth | 88th: Eighty-Eighth |
| 9th: Ninth | 29th: Twenty-Ninth | 49th: Forty-Ninth | 69th: Sixty-Ninth | 89th: Eighty-Ninth |
| 10th: Tenth | 30th: Thirtieth | 50th: Fiftieth | 70th: Seventieth | 90th: Ninetieth |
| 11th: Eleventh | 31st: Thirty-First | 51st: Fifty-First | 71st: Seventy-First | 91st: Ninety-First |
| 12th: Twelfth | 32nd: Thirty-Second | 52nd: Fifty-Second | 72nd: Seventy-Second | 92nd: Ninety-Second |
| 13th: Thirteenth | 33rd: Thirty-Third | 53rd: Fifty-Third | 73rd: Seventy-Third | 93rd: Ninety-Third |
| 14th: Fourteenth | 34th: Thirty-Fourth | 54th: Fifty-Fourth | 74th: Seventy-Fourth | 94th: Ninety-Fourth |
| 15th: Fifteenth | 35th: Thirty-Fifth | 55th: Fifty-Fifth | 75th: Seventy-Fifth | 95th: Ninety-Fifth |
| 16th: Sixteenth | 36th: Thirty-Sixth | 56th: Fifty-Sixth | 76th: Seventy-Sixth | 96th: Ninety-Sixth |
| 17th: Seventeenth | 37th: Thirty-Seventh | 57th: Fifty-Seventh | 77th: Seventy-Seventh | 97th: Ninety-Seventh |
| 18th: Eighteenth | 38th: Thirty-Eighth | 58th: Fifty-Eighth | 78th: Seventy-Eighth | 98th: Ninety-Eighth |
| 19th: Nineteenth | 39th: Thirty-Ninth | 59th: Fifty-Ninth | 79th: Seventy-Ninth | 99th: Ninety-Ninth |
| 20th: Twentieth | 40th: Fortieth | 60th: Sixtieth | 80th: Eightieth | 100th: Hundredth |
Ordinal Numbers 1 to 20
Ordinal numbers from 1 to 20 are different from the rest.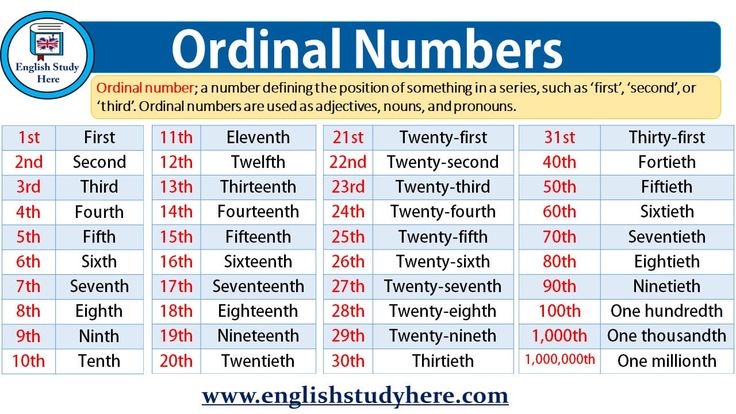 After the number 20, a repeated pattern of ordinal numbers can be observed. Ordinal numbers from 1 to 20 can be listed as follows. 1 - First, 2 - Second, 3 - Third, 4 - Fourth, 5 - Fifth, 6 - Sixth, 7 - Seventh, 8 - Eighth, 9 - Ninth, 10 - Tenth, 11 - Eleventh, 12 - Twelfth, 13 - Thirteenth, 14 - Fourteenth, 15 - Fifteenth, 16 - Sixteenth, 17 - Seventeenth, 18 - Eighteenth, 19 - Nineteenth, 20 - Twentieth.
After the number 20, a repeated pattern of ordinal numbers can be observed. Ordinal numbers from 1 to 20 can be listed as follows. 1 - First, 2 - Second, 3 - Third, 4 - Fourth, 5 - Fifth, 6 - Sixth, 7 - Seventh, 8 - Eighth, 9 - Ninth, 10 - Tenth, 11 - Eleventh, 12 - Twelfth, 13 - Thirteenth, 14 - Fourteenth, 15 - Fifteenth, 16 - Sixteenth, 17 - Seventeenth, 18 - Eighteenth, 19 - Nineteenth, 20 - Twentieth.
☛ Related Topics
- Cardinal Numbers
- Ordinal Numbers Worksheets for Kindergarten
- Numbers
- Rational Numbers
- Prime Numbers
- Composite Numbers
- Even Numbers
- Odd Numbers
- Real Numbers
- Natural Numbers
- Irrational Numbers
- Counting Numbers
Ordinal Numbers Examples
-
Example 1: What is the 3rd letter in the word: SUMMERS?
Solution:
In the given word, SUMMERS, the first letter is 'S'.
The second letter is 'U'. Similarly, we count the position of the letters in order, like, first, second, third, and so on which denotes ordinal numbers. So, we can see that the letter 'M' comes in the 3rd position. Therefore, the third letter in the given word is 'M'.
-
Example 2: Sam, Jenny, Mary, and Jack are standing in a queue in the given order. Who is in the fourth position?
Solution:
From the given information, we can say that: Sam is in the first place, Jenny is in the second place, Mary is in the third place, and Jack is in the fourth place. Therefore, Jack is standing in the fourth position. Here, 4th is an ordinal number because it denotes the position of Jack.
-
Example 3: State true or false with respect to ordinal numbers.
a.) An ordinal number is a number that denotes the position or place of an object.
b.) Ordinal numbers are written as 1st, 2nd, and 3rd, and so on.
Solution:
a.) True, an ordinal number is a number that denotes the position or place of an object.
b.) True, ordinal numbers are written as 1st, 2nd, and 3rd, and so on.
go to slidego to slidego to slide
Ready to see the world through math’s eyes?
Math is a life skill. Help your child perfect it through real-world application.
Book a Free Trial Class
Practice Questions on Ordinal Numbers
go to slidego to slide
FAQs on Ordinal Numbers
What Does Ordinal Number mean?
Ordinal numbers are the numbers that specify the position of objects. For example, when we say that the books are kept on the 3rd shelf, here 3rd is an ordinal number. Similarly, first, second, twentieth, fiftieth, and so on are ordinal numbers.
What is the Difference Between Cardinal and Ordinal Numbers?
Cardinal numbers denote the count of any object. For example, natural numbers like 1, 2 3, and so on are cardinal numbers. On the other hand, ordinal numbers denote the position or place of an object. For example, 1st, 2nd, 3rd, 4th, 5th, and so on, are ordinal numbers.
How to Write Dates with Ordinal Numbers?
Ordinal numbers are used to mention the dates in English. For example, if we need to write the date of Christmas, we write the month and then the ordinal number of the day. In this case, we say that Christmas is on December 25th. Here, 25th is an ordinal number.
Is Zero an Ordinal Number?
No, 0 cannot be considered an ordinal number. Specifying the position of anything as 0th or zeroth does not give a logical explanation.
How to Write Ordinal Numbers?
Ordinal numbers have a suffix added at the end. They can be written as first, second, third, and so on when expressed in words. When ordinal numbers are expressed as numerals, the last two letters of the words are added to the respective numbers, like, 1st, 2nd, 3rd, 4th, and so on.
Why do we use Ordinal Numbers?
We use ordinal numbers for specifying the position or order of something. For example, the pens are kept in the 3rd drawer from the top, or, Ria stays on the second floor of the apartment. Here, the respective numbers specify the position or order of the object or people, whatever the case may be.
What are Ordinal Numbers From 1 to 10?
The ordinal numbers from 1 to 10 are as follows: 1st: First, 2nd: Second, 3rd: Third, 4th: Fourth, 5th: Fifth, 6th: Sixth, 7th: Seventh, 8th: Eighth, 9th: Ninth, and 10th: Tenth.
What is the Ordinal Number of 1?
The ordinal of 1 is written as First. In the numeral form, it is represented as 1st.
Download FREE Study Materials
Worksheets on Ordinal Numbers
Ordinal number | it's... What is Ordinal Number?
Ordinal number , ordinal (lat. ordinalis - ordinal) or transfinite number (lat. trans - beyond, through + finitio - edge, limit) in the theory of sets - "beyond infinity". First introduced by Georg Cantor in 1897 with the aim of classifying well-ordered sets. They play a key role in the proof of many theorems of set theory, especially in connection with the related principle of transfinite induction.
|
Contents
|
Definition
Ordinal numbers allow for various variants of equivalent definitions in one sense or another. One of the modern formulations of the definition of an ordinal number according to von Neumann is as follows:
- Let's call the set transitive if each element is a subset of : .
- A set satisfying the foundation axiom is called an ordinal , or an ordinal if it and each of its elements are transitive: .
Note that the foundation axiom is essentially used in this definition, which must be taken into account when working with axiomatic systems other than the Zermelo-Fraenkel system.
Ordinal numbers are usually denoted using lowercase Greek letters. This article adheres to such notation.
Properties
- If is an ordinal number, then each element is an ordinal number.
- Exactly one of the following relations holds for any:
- Any set of ordinal numbers is well ordered by the relation (in particular, any ordinal number considered as a set is well ordered by the relation ), and is the smallest element of the set , is an ordinal greater than or equal to any of the elements of the set . The expressions and for ordinal numbers are equivalent. The following assumes that ordinal numbers are compared using the relation
- For any well-ordered set there exists a unique ordinal isomorphic (in particular, for any set of ordinals there is a unique ordinal isomorphic to it).
- Any coincides with the set of all ordinal numbers less than .
- The starting segment of any ordinal number is an ordinal number.
- The empty set is the smallest ordinal number (which means it is an element of any other ordinal number).
- is called regular (synonym: unlimited ) if either it is equal to , or there is an immediately preceding it, in other words, if it exists but no other ordinal number can be inserted between them. , and write: (sometimes just what turns out to be consistent with the notation for the sum of ordinal numbers).
- Ordinal numbers that are not nonlimiting are called limit ordinal numbers (sometimes also referred to as limit ordinal numbers).
- The set of all finite ordinal numbers is isomorphic to the set of non-negative integers, and the same notation is used for them as for integers. In this case, the operations of addition, multiplication and exponentiation for ordinal numbers are transferred to the corresponding operations for integers.
Several first ordinal numbers:
- The set of all finite ordinal numbers is denoted by . It is the smallest limiting ordinal number and the smallest infinite (namely, countable) ordinal number. The next serial number is
- The finite condition can be written as or, which is the same,
- There is an infinite set of ordinal numbers, but there is no set of all ordinal numbers. In other words, the collection of all ordinal numbers is a proper class.
- Each set of ordinal numbers is bounded from above and has a least upper bound, which is denoted by
- If - limit ordinal or , otherwise
- The least upper bound of a countable set of countable ordinal numbers is countable.
- Every ordinal number has a unique representation in Cantor normal form ( eng. ).
Ordinal arithmetic
Operation definitions
- The sum of ordinal numbers is determined recursively as follows:
- where the third rule applies when is the limit ordinal.

- Using the same notation, we define the operation of multiplication:
- Using the same notation, we define the exponentiation operation:
Properties of operations
- Ordinal addition is noncommutative; in particular
- Ordinal addition is associative: which allows you to write the sum of several terms without brackets.
- The sum increases with the growth of the right term and does not decrease with the growth of the left term: it follows from
- If then there is a single ordinal for which
- Ordinal multiplication is non-commutative; in particular
- Multiplication of ordinal numbers is associative: which allows you to write the product of several factors without parentheses.
- Addition and multiplication are left distributive:
- If the arguments are finite, addition, multiplication, and exponentiation are converted to the corresponding operations for integers (with final results).

- If the arguments are countable, the results of addition, multiplication and exponentiation are also countable.
See also
- Cardinal number
Literature
Ordinal and quantitative counting for preschoolers
11/24/2020
To teach a child to count even before he becomes a first grader? Easily! To do this, you need to awaken in a preschooler an interest in mathematics and simple calculations. Of course, the game will help in this! Playfully, you can learn not only to count, but also to distinguish a quantitative account from an ordinal one. Forgot what it is and what is the difference? We invite you to refresh your knowledge.
Mathematical counting is the act of counting something. The school teaches ordinal and quantitative counting. Let's talk about them.
Contents:
- What is a quantitative account
- What is an ordinal account
- Ordinal and quantitative accounts - 5 differences
- Targets
- Numerals
- Questions and answers
- Direction
- Meaning
- Reinforcement games
- "On the clouds" with an ordinal score of
- Number and Ordinal Counting Game - Rainbow Arc
- Game - Luntik's birthday
- Helpful Hints
What is a quantitative account
A quantitative account implies the answer to the question: "How much?".
As soon as the child remembers the question, he will understand what is required of him. Of course, information is best absorbed in the form of gaming exercises.
Example: Place objects in front of the baby. Ask him a question, give him the opportunity to count and answer.
The game can be gradually made more difficult. For example, adding or removing some of the items, grouping according to characteristics, etc.
What is an ordinal score
An ordinal score is associated with the question: "What is the score?".
It's simple. Again, the game and objects, preferably something different from each other, for example, felt-tip pens. Ordinal from the words "order, in order", this will help the child remember the main question. Ask him to determine the serial number of any of the items.
To complicate the game tasks, swap items, take away or add new ones, asking the child to explain how and why the serial number changes.
Ordinal and quantitative accounts - 5 differences
Only an account is common between them. You have to count to get the answer to the question in the end. Everything else is different:
- targets;
- numerals;
- questions;
- direction;
- value.
Difficult at first glance. For a preschooler, it may even be incomprehensible, but if you play a little, everything will become clear!
Goals
A quantitative account is used to count something. The end goal is to determine the total number. An ordinal count is needed to determine the number of an item in an ordered set.
A simple example. Arrange the fruits in a row: apple, pear, tangerine, orange and pomegranate. A quantitative account will help us calculate how many fruits are on the table - 5.
Ordinal is needed to determine the ordinal number of each fruit in the row. The apple is the first, the pear is the second, the tangerine is the third, the orange is the fourth and the pomegranate is the fifth.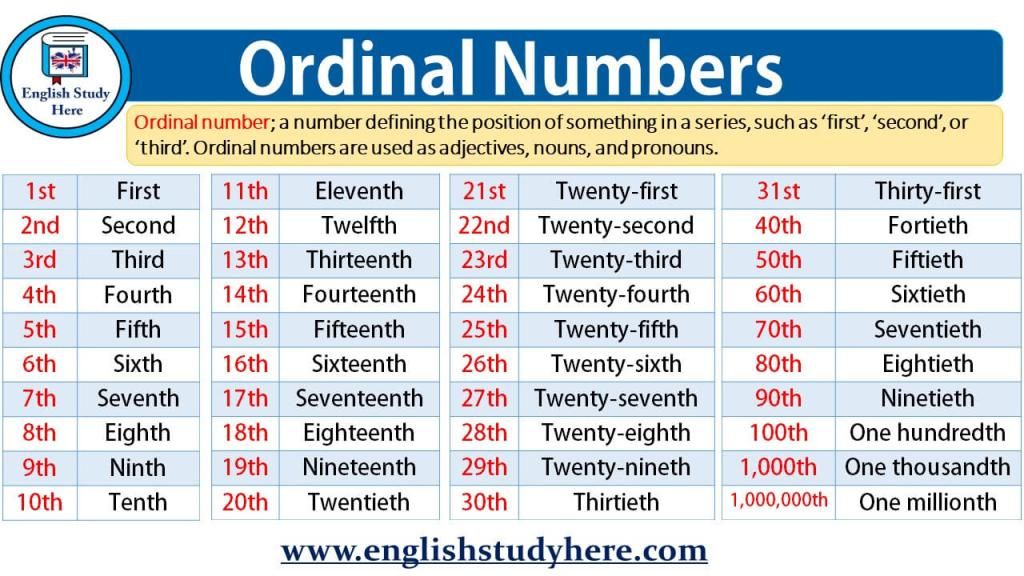 The same can be done from right to left, the serial numbers of fruits in this case will change.
The same can be done from right to left, the serial numbers of fruits in this case will change.
Numerals
Ordinal counting is impossible without ordinal numbers (indicate the order of an object in a series of sequences), and quantitative counting is impossible without quantitative ones (indicate the quantity).
For example, one, two, three are quantitative, the first, second, third are ordinal numerators.
Questions and answers
It is easiest for children to remember how the ordinal count differs from the numeral count by asking questions. "How many?" - numeral, "what, what number?" - ordinal.
This example game can be played all day long until the child memorizes the information. Ask questions about everything around him. For example:
How many legs does a stool have?
How many fingers are on the hand?
How many rooms are there in the apartment?
or
What floor are we on?
What candy do you eat?
Direction
To calculate how many items in total, it does not matter how to do it from right to left or vice versa. The goal is to determine the total. You can find out the number of an item in a set only after specifying the direction. Ordinal numbers change depending on whether you count from right to left or vice versa.
The goal is to determine the total. You can find out the number of an item in a set only after specifying the direction. Ordinal numbers change depending on whether you count from right to left or vice versa.
Example:
Show the third bird from the right?
What color is the second house on the left?
These are tasks for determining the sequence number with direction. Explain to the child that the total number of objects does not change when the direction changes.
Meaning
The quantitative score indicates the totality of items, and the ordinal score helps to determine the place of each.
Games to reinforce the material
"On the clouds" with an ordinal score
An interesting game to reinforce the ordinal score with the smallest. To play, you will need any small toy smaller than an A4 sheet. The toy is the main character of the game. She will ride on fluffy clouds.
Ordinary white sheets of A4 format are suitable for the role of clouds. By the way, by inviting your child to imagine the sheets in the form of funny clouds, you will push him to dream up a little.
By the way, by inviting your child to imagine the sheets in the form of funny clouds, you will push him to dream up a little.
So what needs to be done. Lay out the sheets-clouds in a row. Place the toy on any of them. Start asking questions:
How many clouds, let's count?
Are all clouds the same?
Can you show me where the toy sits?
How can we find out which cloud she is riding?
Answering the questions, the child will count the clouds, he will be able to find out for himself that the toy is sitting on the first, second or third. You can play this game for a long time. The toy will soon get bored on its own cloud, it will want to transfer to another one, and then to the next one, and so on. As you play, keep asking your child probing questions.
Number and Ordinal Counting Game - Rainbow Arc
You will need multi-colored identical objects. Ideally 5-7 colors. It can be anything - from building blocks and cubes to carved figures from cardboard, balls, plastic plates, etc.
To reinforce quantitative counting, simply ask your child to count objects. Complicate the tasks by grouping them by color or some specific features.
When practicing ordinal counting, invite your child to name the number of an object by color and vice versa. For example:
What color is the third ball in a row?
What is the blue cube on the right?
Show me the second clothespin from the left, what color is it?
Change objects, direction of counting, number before the child begins to lose interest in what is happening.
Game - Luntik's birthday
If the child does not know or does not like Luntik, you can replace him with any other cartoon character. So how to play.
Cut out 5 identical balloons on a stick with your child or on your own. Under one draw a birthday cake. The purpose of the game is to fix in the mind of the child the idea that the serial number always points to a specific object and depends on the direction of the count.
The essence of the story is as follows. Luntik has a birthday. All the guests decided to give him a balloon. But someone could not resist and prepared a birthday cake for the birthday boy. Luntik knows that a surprise awaits him. The caterpillars told him about this in secret. But apart from the fact that the guest who brings the second ball will have a surprise, he does not know anything!
Task: Find the second ball and make sure that Luntik gets a cake with it. To begin with, try to do it for the birthday man. For visibility, let him begin to count from the wrong end, skip the balls or swap them. The main thing is to clearly show the baby that the direction of the account affects the final result.
Variations of the game are different. You can swap balls, pick up, add, etc. Each time the child must determine what has changed, why, what has become the serial number of the balloon with a birthday cake.
Helpful Hints
To get kids under 4 interested in counting in the summer, tell them that it will help them find out the total number of items and find a place for each.