Pre k math concepts

The 4 Major Math Concepts Your Kids Learn in PreK & Kindergarten

There are so many different topics our children learn throughout the year, just keeping up with each night’s new piece of homework and its latest ideas can feel very overwhelming. As parents, we don’t get to see the major idea behind the “everyday” work and it can be frustrating to understand where each skill is going. In this first blog post of a continuing series, I will be highlighting the major math concepts that are taught at the different grade levels so we, as parents, can help to build and support these ideas at home.

Here are the four major math concepts taught in pre-kindergarten and kindergarten, along with exercises you can practice with your children to help reinforce their learning.

1. Counting. Students are beginning their experience with numbers through counting, number names and written numerals. Students are learning to count objects and understand a one-to-one correspondence. They are also starting to compare different sets of objects and use appropriate language.

Encourage your child to:

• Touch different objects and count out loud.
• Move objects from one group to another.
• Count a set of objects and “see” or “write” that corresponding number.
• Start to use comparing words: more than, less than, the same as.

2. Addition & Subtraction. This is the very early stage of adding and subtracting. The focus should be on developing an understanding of addition as “putting together and adding to,” and subtracting as “taking apart and taking from.” Students do not need to write equations at this young an age, but are encouraged to begin using them.

Encourage your child to:

• Tell stories about adding and subtracting. For example, for addition: Two bunnies sat on the grass. Three more bunnies hopped there. How many bunnies are on the grass now? For subtraction: Five apples were on the table. I ate two apples. How many apples are on the table now? Draw pictures about putting together and taking apart.
• Count to 10 and break apart numbers (decompose – math’s fancy word for “breaking apart”) into different combinations. For example, 5 can be seen as:

Image Credit: http://kindercraze.com

3. Measurement & Data. Young children are beginning to describe and compare their physical world. They are starting to classify, sort and group objects into categories.

Encourage your children to:

• Compare two different objects using appropriate language. For example:
  “John is taller than Sarah.”
  “This tree is shorter than that tree.”
  “My bag is heavier than your bag.”
• Sort objects by color, size, material, etc.
• Describe their physical world with directional words: in front of, behind, on top of, next to, below, etc.

4. Geometry. Students are starting to look at and compare two-dimensional (flat) and three-dimensional (solid) shapes. They are using appropriate language to recognize different shapes and talk about their attributes.

Encourage your child to:

• Find 2-D shapes in the world: squares, circles, triangles, rectangles, and hexagons.
• Find 3-D shapes in the world: cubes, cones, cylinders, and spheres.
• Count the different number of sides, vertices, angles, etc.Model different shapes using clay, sticks, pipe-cleaners, etc.

See all blog posts in this series for information on what your child will learn in math class from preschool all the up through 8th grade. 

The Most Important Math Concepts Kids Learn in Pre-K

Although there’s a lot of emphasis placed on emergent reading, experts show that pre-k math skills are just as important for your child’s learning development.

Understanding what skills your child will be exposed to as a math beginner will give you an idea of what concepts you can emphasize in fun, easy ways at home!

Fortunately, kids are exposed to many math concepts from a very young age — putting puzzles together, sorting objects, and even playing with building blocks. These activities all help build a good foundation for math.

In this article, we’ll take you through the most important pre-k math concepts so you can encourage and motivate your budding mathematician!

Table Of Contents

• What Are The Components Of Pre-K Math?
• Basic Pre-K Math Checklist
• Pre-K Math Development
• 9 Fun Pre-K Math Activities

What Are The Components Of Pre-K Math?

There are five basic components of pre-k math. They act like umbrella terms, each with many different elements hidden inside their broad concepts.

Your child will become acquainted with all of these essential concepts when they begin learning pre-k math.

1) Numbers And Counting

Children typically start with the bedrock of math — numbers! They’ll learn number names and how to write numbers, typically beginning with 1-10.

Counting is not easy business! While your child learns how to count — first with physical objects, then conceptually — they are bound to make mistakes here and there. This is perfectly all right. Counting will take time to master.

Most of kids’ initial exposure will be through representational counting. This could mean counting the number of strawberries in their lunch box, how many blocks are on the floor, and so on. These counting activities will set the stage for a strong foundation in counting.

By understanding that numbers represent objects, your child will begin to understand one-to-one correspondence (each object counted gets its own number and only that number) as well as the counting principle that when counting the number of objects, the last number counted equals the amount present.

Over time, a child’s reliance on physical objects for counting will decrease. They’ll depend more on conceptual counting as their skills develop.

This conceptual counting is called “number sense.” They’ll understand that quantities, whether tangible or theoretical, are countable. They’ll also learn that numbers can be compared: two or more numbers can have a more-than, less-than, or same-as number relationship.

There are many fun ways to get your child comfortable with numbers and counting at home without making it feel burdensome.

Here are a few simple yet effective strategies you can try:

• Encourage your child to touch and count objects they see in everyday life — for example, a bunch of bananas or a stack of books.
• After they count a set of objects, help them write down the corresponding number on a piece of paper.
• Have your child compare different items using the appropriate language. For example, “Let’s count the number of blueberries and strawberries on the plate. Are there more strawberries than blueberries?”
• Hang a simple number line on the wall or tape one to your refrigerator. Throughout the day, point to each number with your child and count from 1-10 together.
• Ask your child to help set the table by counting out the right number of forks and spoons. Once they have collected them, they can count them again as they put one at each place setting.

These simple activities allow children to make sense of numbers. And the more they practice counting principles outside of the classroom, the more they’ll realize how relevant they are to everyday life.

2) Addition And Subtraction

Once your child has a firm grasp on counting and is developing number sense, they’ll explore the relationships between numbers more often. Describing how numbers are the same or different will lead into learning how to combine two numbers to make a new number!

Similar to the last concept, children will typically learn how to add and subtract by relying on counting activities with tangible objects. For example, you could set up two separate groups of apples and ask how many you will have if you join them together.

The first group may have three apples, while the second group has two apples. At first, many children will count one group and then start over to count the second group. It is a good idea to count both groups individually and then bring them together and count the total amount.

This is their first introduction to addition! The same idea works for subtracting. What happens when you begin with five apples and then take away two of them?

“Taking away” objects may be a little harder for your child to master at first. This is why many children will remove apples first and then count the remaining apples rather than counting backward.

To help, practice counting backward together. Pretend to be a rocket ship, and start counting down from five to one, gradually increasing the beginning number each time. After you get to one, shout, “Blastoff!” and jump into the air as high as you can. This fun game can help your child become more comfortable with counting down.

Pictures can also help your child master addition and subtraction concepts. For addition practice, present one sheet of paper with three apples and another with two. Then say, “Count the apples on both pieces of paper. How many apples do you have total?”

For subtraction problems, present this scenario: “On our paper, we have five apples total. How many apples will you see if I cover up two of them?” Then, count the remaining apples together.

Pictures are an effective way for your child to visualize mathematical problems. But, if you prefer not to draw, you can also use real objects instead. You could get out several apples (stuffed animals, cups, or whatever) and count them. Then, use those items for math practice.

Remember that adding and subtracting are basically making comparisons between numbers or establishing relationships between them. There are many strategies a child might use to solve a problem, which is a good thing since our main goal is to help children think mathematically.

3) Geometry And Spatial Reasoning

Shapes are everywhere in our world, which will be one of your greatest assets when it comes to teaching your child about shapes and spatial reasoning.

They’ll start out by learning about the basic 2-D shapes that are used in math: squares, triangles, circles, rectangles, rhombuses, and ovals. Learning how to draw these basic shape illustrations can be helpful for their learning process.

Some of these shapes you’ll be able to reference easily in your day-to-day life. This will help reinforce your child’s understanding of the shapes after their initial introduction.

For example, when making breakfast with your child, you could hold up a plate and ask them, “What shape is this? Do you think it’s a square or a circle?”

Other shapes, like triangles or rhombuses, may be a little harder to find hanging around. Challenge your child to find these shapes in nature. Are there any flower petals in your garden that are shaped like triangles (or an aloe vera plant hanging in their windowsill)?

Encourage your child to be creative with identifying shapes! It will help them with learning geometry in the long run.

Next, learning 3-D shapes will come after learning 2-D shapes. Like their flatter cousins, 3-D shapes are all around the world, too! Your child’s soccer ball is a sphere; the paper towel roll in the kitchen is a cylinder.

We recommend learning the basic form of these shapes and how they appear first. Then, you can use the natural 3-D shapes in your child’s environment to reinforce their learning!

Point out shapes when you see them and play a shape version of “I Spy” to practice. If your child has a set of blocks, talk about the different shapes of the blocks. Challenge them to use only one shape to build something. Then, see what they can make by using all of the shapes.

Kids also learn about spatial reasoning by discovering how to describe the shapes they see and play with. They can compare them with dimensional adjectives like “big” and “small,” or characteristics of their shape like “straight” and “curvy.”

This includes the spatial relationship between different objects, too. Look out for observations using location adverbs like “under,” “beside,” or “around.” These are all different ways for your child to “measure” or observe how shapes take up space.

4) Sorting And Patterns

We categorize things in our daily lives without even realizing it. Your child probably already does this, too — they may arrange their stuffed animals or toys in a certain way. For example, they may keep farm animals separated from dinosaurs.

Sorting and patterns are related to categorical reasoning. In the same way grocery stores sort out items by their parallel uses, your child will learn how to sort things based on their characteristics and how they are the same or different from other objects.

They’ll sort objects by weight, shape, quantity, texture, color, and other traits, often without even realizing it!

It’s important to note here that sorting and counting aren’t sequential. Your child might begin sorting before they begin counting, in fact.

For instance, if you want your child to sort a bowl of fruit, you can ask them to count all of the strawberries. They’ll sort the strawberries from the rest of the fruit. If you ask them to count the red fruit, they’ll sort out strawberries, cherries, and watermelon and count them together.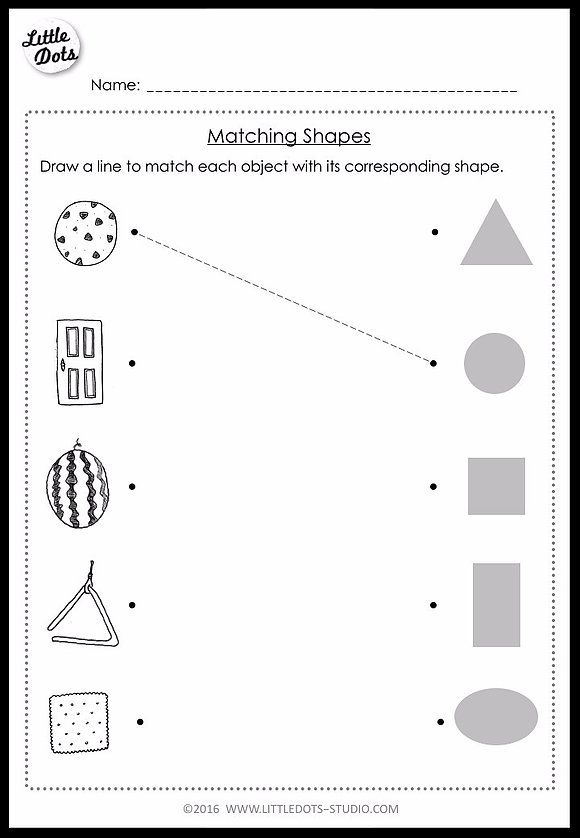

Once a child has learned to isolate characteristics, they can begin to identify, extend, and even create patterns. Your child will learn how to:

• Copy a pattern
• Identify the parts that repeat and continue a pattern
• Correct a mistake in a pattern
• Explain a pattern
• Create their own patterns

To encourage your child to explore patterns, take a few moments to build a pattern for them when you play together. Use whatever materials you have available and create a simple AB pattern, such as truck, car, truck, car.

Next, point to each object. Say its name aloud. Then, when you get to the end of the row, ask them what comes next. If they aren’t sure, grab the next object and put it down. Once you’ve completed one round, start at the beginning and repeat each item to reinforce the pattern.

5) The Language Of Math

Part of learning how to do math means learning how to “speak” math. We don’t mean your child will turn into C-3PO — just that they will learn how to use mathematically correct language, or how to tell a story with math terms.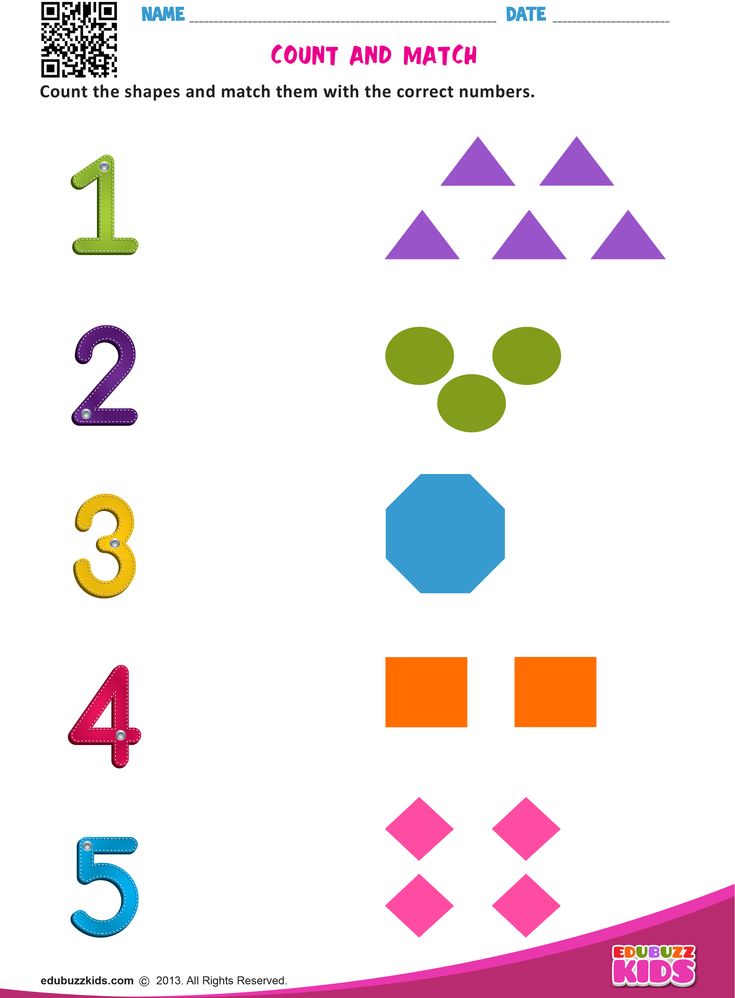

This can happen in daily life. While picking at an afternoon snack, your younger child may say, “Hey! My brother has more crackers than me!” Then you might agree to “add” to the cookies on the younger child’s plate so that both plates are “equal.”

These skills may be naturally exciting for your child — they’ll feel like they’re learning how to speak “grown up!” Show them how fun it is to incorporate mathematically appropriate language into their daily speech and use it to tell stories about what’s going on around them.

Using words to describe things in their lives will help them give ownership over ideas and observations. Motivate them to think about the order of the world around them and use different words to describe them, such as:

• More than
• Less than
• Shape names
• Light or heavy
• Small or big

Mastering math language will help them in their quest to become robust mathematicians! It’ll also help them develop a strong vocabulary so they’re better prepared for kindergarten.

Basic Pre-K Math Checklist

Now that you know some of the concepts your child will be learning in pre-k math, let’s look at some of the skills they’ll build during this time.

• Rote count to 10
• Use one-to-one correspondence to count up to 10 objects and tell how many there are altogether
• Recognize basic shapes (circle, triangle, square)
• Understand the concept of quantity (more/less)
• Sort objects by one characteristic
• Understand and use directional terms, such as up, down, in, out
• Pick what object goes next in a simple pattern

While these aren’t all of the math skills your child might learn in pre-k, they will give your child a solid mathematical foundation to build on in kindergarten. And they’re all skills you can practice in fun ways!

Pre-K Math Development

As your child grows and learns, they’ll work through three phases of mathematical development: concrete, representational, and abstract. They’ll likely be in the concrete stage at the beginning of pre-k.

During this phase, students need hands-on activities and real-world examples to help them understand mathematical concepts. This is why math manipulatives are so crucial in the early years. It’s also essential to present math concepts in a very concrete way during this stage.

For example, if you’re teaching your child about numbers, don’t just tell them that five is more than three. Instead, show them five objects and three objects, and let them count for themselves. This will help them understand the concept of more and less.

As your child continues to learn and practice a mathematical concept, they can move into the representational phase. Here, students can count pictures or images instead of actual objects. For example, they realize that numbers can be represented by lines or drawings.

Then, they’ll be ready to try the abstract stage. At this point, children understand that numbers can be represented by symbols.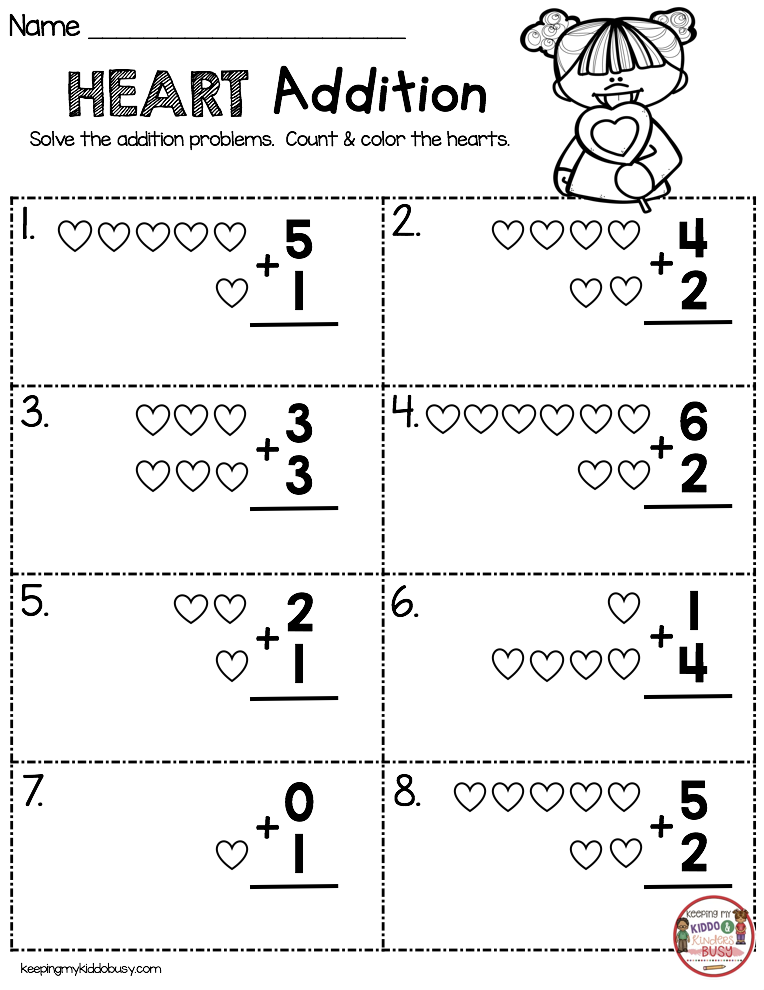 They don’t need manipulatives or visual aids to do math problems. They can start using numbers and symbols such as + or – to solve math problems.

The activities above will help your child to build their understanding of mathematical concepts so they can move through the different stages.

But, in pre-k, it’s important to focus on the process, not the answer. So don’t worry if your child doesn’t get the solution right away. Let them work through the problem and try to figure it out for themselves.

A strong foundation in pre-k math sets children up for success when they start kindergarten. By providing opportunities for them to explore and experiment with math, you can help them develop the skills they need to be successful in school and beyond.

9 Fun Pre-K Math Activities

Now that you’re clear on all of the exciting new math concepts your pre-kindergartener will be exposed to and what skills they’ll practice, let’s talk about some games and activities you can play at home to help your child hone them.

We’ve already discussed some math activities you can incorporate into everyday life. Now, we’re sharing our list of fun games to encourage your young learner to love math even more.

1) What Did I Do?

This game helps reinforce counting, adding, and subtracting. It’s quick to play, so it’s perfect for when you have a few extra minutes.

What You’ll Need

• Small objects (e.g., paper clips)

What To Do

Place some paper clips (or any other small objects) in your hand, and let your child count how many you have. After they’ve done this, put your hands behind your back and either add or remove some.

Next, show your child the new quantity and ask them to count how many there are now. You can ask your child questions, such as, “Did I add or take away some paper clips?” or “How many did I add or take away?”

For even more fun and learning opportunities, take turns playing the game. And when it’s your turn to guess, it’s OK to guess wrong — “I think you took away 10!… No! I added two!” This back and forth offers lots of laughs and critical thinking for your little mathematician.

Remember that because your child is in pre-k, the concepts of addition and subtraction are still new. Therefore, it’s best to keep the number of objects used in this game low (e.g., 1-10 clips) so they aren’t confused or overwhelmed.

2) Math Tic-Tac-Toe

Add a mathematical twist to the classic game of Tic-Tac-Toe!

What You’ll Need

• Paper
• Pencil
• Ruler
• Markers (or colored pencils)

What To Do

Start by dividing your sheet of paper into squares by drawing lines (three horizontal by three vertical). In traditional tic-tac-toe, you’d leave these squares blank until the game starts. Not this time.

For this version of the game, you’ll need to fill each box with dots and have your child tell you how many dots are in a box before placing their X or O in it. The first player to get three Xs or Os wins!

The Xs or Os don’t have to be in order at this point, but you can add that requirement as a challenge once your child gets the hang of playing the game.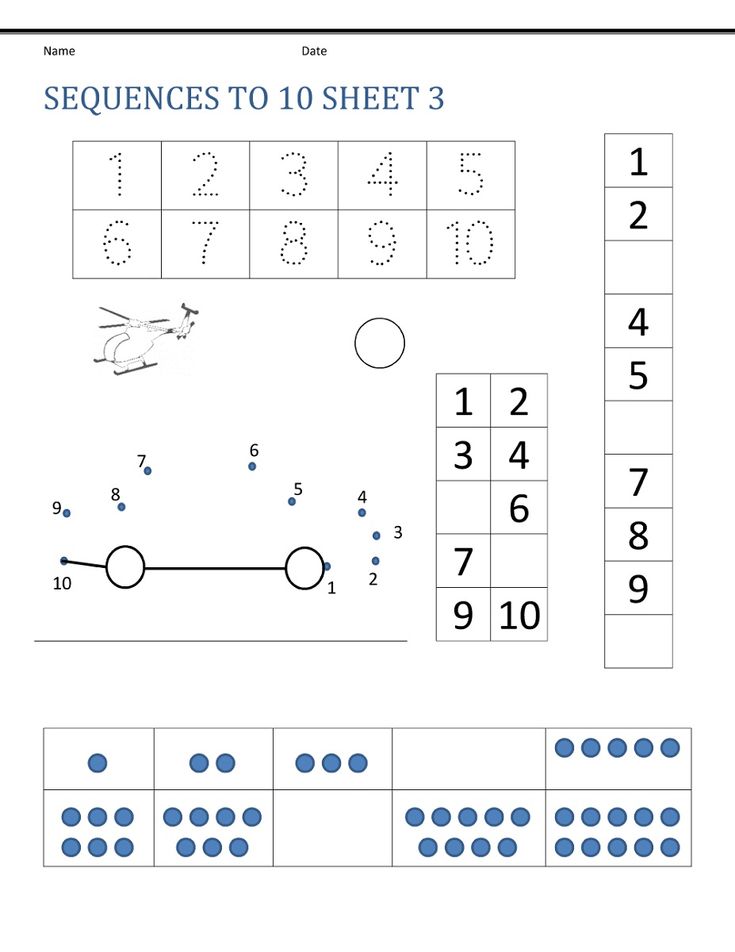

This activity helps kids work on their counting skills while also incorporating lots of fun.

3) NumberBow

Your child will add numbers to create a beautiful rainbow in this game.

What You’ll Need

• Two dice
• Two sheets of paper
• Colored pencils (or crayons)
• Pencil

What To Do

Draw two identical rainbow-shaped boards (one on each sheet of paper) with numbered boxes on the rainbows. (You can check out this link for reference.). The aim of the game is to color the numbered boxes in.

To play, each player throws two dice, then adds the numbers from the throw together and colors in the corresponding box on their rainbow.

For example, if your child throws a three and a one, they’d need to add 3+1 and color in the “4” box. If they’ve already colored that box in, they’d have to wait for their next turn. Each player gets 10 turns to have the most colorful rainbow at the end!

While this is an effective game to help your child work on their addition skills, some children might experience difficulty adding larger numbers together (e.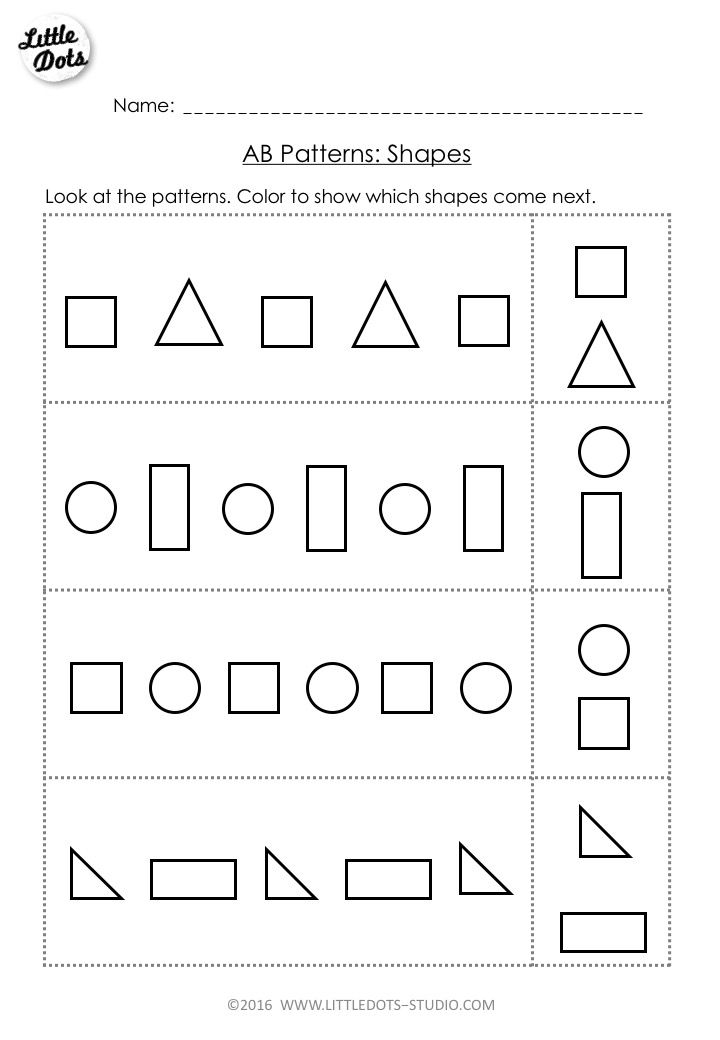 g., 5 and 6). If you need to help them, that’s OK!

Remember that exposure and repetition are very beneficial for young learners.

4) Fill The Cup

This game can be challenging for younger children, so if it causes frustration, play other math games until your child is more comfortable with adding and counting.

What You’ll Need

• Dice
• Plastic cup
• Small objects that are easy to count (e.g., paper clips, dried beans, pebbles, etc.)

What To Do

To begin the game, players roll the dice at the same time. The number rolled indicates the number of items you can add to your cup. For example, if you roll a five, you add five dried beans. The goal for your child is to be the first one to fill their cup.

At the pre-kindergarten stage, some children might not be comfortable with the steps needed to play this game (rolling the dice, reading the number aloud, adding the items to the cup). So, before starting, take a few minutes to get them used to the process.

If you notice that it’s still too challenging, you can make it easier by choosing to roll the dice for each other. In this option, you can roll the dice and then help your child read the number and add the right amount of items to their cup.

Whichever variation you choose, this is a fun and engaging way to help children learn numbers and practice counting.

5) Stand Up, Sit Down

Kids enjoy playing this active game where they get to use their bodies and their brains! (Note: This game requires more than one child player, so it’s a great activity for siblings or to do when your child has a friend over.)

What You’ll Need

• Index cards
• Marker

What To Do

Write the numbers 1-10 on the index cards (one number per card) and hand three to each participant. Then, say a math equation (or word problem) out loud.

If the answer matches a number they’re holding, the child will stand. If they don’t have the answer, they remain seated.

For example, if the question is, “If I have three dried beans and I throw away one, how many do I have left?”, the child with “2” would then need to stand up and show their card.

The player who has the least number of cards left at the end of five rounds wins. Note: To make it easier, you can give children small items (e.g., blocks, dried beans, paper clips, etc.) to help them count.

Stand Up, Sit Down is also helpful for children learning shapes. Instead of writing numbers on the cards and handing them out, you can draw different 2-D and 3-D shapes that children learn in pre-k (as discussed above) and hand those out.

To play, someone describes a shape and the player who has that shape stands up and says what it is. For example, “If you are holding a shape that has three sides, stand up right now!”

When the child stands up, they’ll need to say that their shape is a triangle, and they get the point. In this version of the game, the player with the most points at the end wins.

Using this game allows children to learn the names and attributes of the different 2-D and 3-D shapes they get exposed to in pre-kindergarten.

6) Who Has More?

This game is perfect for helping kids understand the concepts of more and less, which are critical in early math development.

What You’ll Need

• A small bowl or container
• A teaspoon
• A handful of objects (e.g., buttons, pennies, cereal pieces, etc.)

What To Do

Place the objects in one bowl. Have your child scoop a teaspoon of them out and count them. Then, you do the same and see who got the most. That person’s the winner!

Note: Counting past 10 is difficult at this age, so you’ll want to use big enough items (such as large kidney beans) and stick to a teaspoon for scooping so your child doesn’t end up with more than 10 per spoonful.

7) Read Math Books

Help your child develop a love for math by reading math-related books together.

What You’ll Need

• A mathematical-themed book to read together (see some recommendations below)

What To Do

Grab one of the following books and snuggle up with your little one for a math-themed storytime. As you read, point out any mathematical concepts in the book.

• From the Garden by Michael Dahl
• The Shape of Me and Other Stuff by Dr. Seuss
• The Button Box by Margarette S. Reid
• A Pair of Socks by Stuart J. Murphy
• The Berenstain Bears and the Spooky Old Tree by Stan and Jan Berenstain
• Pattern Fish by Trudy Harris

When you finish reading, discuss any new math concepts your child learned. You could even do a related activity or two to reinforce what they’ve learned.

8) In The Box

This game helps your child practice prepositions or direction words, like “under,” “behind,” and “in front of.” These concepts are essential for mathematical development as well as reading comprehension.

What You’ll Need

• A stuffed animal
• An empty box large enough for the animal to fit inside

What To Do

Ask your child to put the animal inside the box. If they have difficulty understanding what you mean, give them some clues. For example, you could say, “Put the animal in the box so that its head is sticking out,” or “Put the animal in the box so that only its tail is showing.”

Once the animal is in the box, ask them to describe where it is using prepositions. So, they might say, “The animal is in the box.”

Then, take the animal out and place it behind the box. Ask your child to describe its location again. For example, they might say, “The animal is behind the box.”

Next, let them take a turn placing the animal in, on, under, next to, etc. the box. When they’re done, you describe where it is. Continue taking turns as you practice different prepositions.

9) Number Line Race

This game helps kids with number recognition as well as one-to-one correspondence.

What You’ll Need

• Number cards (we recommend the ones from the HOMER Explore Numbers Kit)
• A die

What To Do:

Spread the cards out in numerical order, with a bit of space between each one. They should form a line on the floor, though it doesn’t need to be perfectly straight.

Have your child stand on the card with the number one on it. Hand them the die and let them roll it. Call out the number they rolled. Next, ask them to move that many numbers forward, moving from one index card to the next as they count aloud.

If they land on a number that would take them off the end of the line, they start from the beginning for their next throw (each player gets five throws). Then, it’s your turn! Start on one and see how far you can get, too.

The person to end on the card with the highest number is the winner!

Encouraging A Love Of Pre-K Math At Home

Pre-k math isn’t just reserved for pre-k classes. You can help your child explore the exciting world of pre-k math right from your home!

HOMER is always here to help and happy to be your at-home learning partner. Our Learn & Grow app offers tons of opportunities for your child to develop their pre-k math skills from conception to execution.

Our games are personalized to accommodate your child’s specific interests. They include pattern-identification games like Ribbons or shape-building games like the Castle Creator.

Your child can also explore the Shapery Bakery, where they help the cute, cuddly Tisa the Cat by sorting treats based on their shape. All that and so much more can help your child develop their pre-k math skills!

Author

Philosophy of Mathematical Knowledge and Problems of Computer Education

The problem of finding such algorithms for computers, which can be used to simulate some real processes, has been solved. The philosophical and methodological aspects of computational mathematics are considered in the context of modern problems of computer education.

Keywords: mathematical knowledge, computer mathematics, philosophy of mathematics.

The computer can be considered the most revolutionary technical invention of the last century. This powerful tool, originally created for mathematical calculations, made it possible to carry out mathematical modeling of huge classes of various natural-science and social-humanitarian processes, explicating new educational perspectives of mathematical knowledge.

The advent of computers not only changed the face of the entire civilization, but also gave rise to doubts about the reliable methodological validity of machine methods for proving mathematical theorems. In this regard, a philosophical problem arose: how to understand and apply such results? The main methodological idea is that this is a way of obtaining new information that was not previously visible in the usual strictly mathematical formalism.

Computational mathematics

There are two types of problems and results in teaching mathematics. Some of them concern the fact that mathematics exists in itself. Others concern the results of the possibilities of our activities. In classical mathematics, questions of the "second plan" - about calculations and constructions - played a subordinate role. But now their meaning has changed significantly.

Even the most insightful philosophers of mathematics in the first half of the twentieth century. could not foresee the emergence of such a powerful new direction in modern mathematics as computational mathematics (VM). For definiteness, by "computational mathematics" we mean the area of ​​modern technologies related to mathematical calculations.

What contributed to the fundamental change in mathematics? The trivial answer is an increase in the practical need for calculations and the use of computers. But the deep essence of such a radical change in cognitive mechanisms is by no means in this. The process by which the human mind understands mathematical propositions is quite different from what we can get from a computer. Only within a mathematical framework can we count on the possibility of any rigorous demonstration of the non-computability of at least some part of our conscious activity, since the question of computability by its very nature is, of course, mathematical.

Thanks to new theories of mathematics, such as algorithm theory and game theory, as well as information technology, the study of human action is also included in the field of mathematics, contributing to the modeling of understanding. From the ability of mathematical theories to complete stabilization follows such a feature of their development as the cumulative nature of mathematical knowledge. This characteristic indicates the possibility of storing and cumulating the results of mathematical knowledge through the classification of mathematical theories arranged in a hierarchical order. Its essence lies in the fact that new stages in the development of mathematics do not eliminate the results of previous theories as false, but in the vast majority of cases they completely confirm them, changing only in terms of their linguistic design, i.e. assimilated into new concepts.

As for the development of computational mathematics, A.S. Narignani characterizes it as follows: “The current state of affairs in the WM can be assessed by confronting two alternative points of view. One, as if for granted: VM is a successful, rapidly developing area, extremely demanded by practice and basically meeting its needs. The second, far from being so optimistic, is that the VM is in a deepening crisis, proving to be more and more inadequate in the context of the growing demands of practice” [1. S. 71]. Since the market of the most demanded tasks of computational mathematics in the context of modern computer education is too vast and diverse, then only the statement of the crisis and the identification of its causes does not solve the problem of its potential development.

This requires a preliminary philosophical analysis of the basic concept of computational mathematics and its methodological paradigm. On the one hand, the widespread introduction of computer education and the development of new information technologies contribute, first of all, to a qualitative change in the organization of information resources, including their storage and access to them. On the other hand, one of the main reasons for the limited possibilities of the heuristic potential of a computer experiment in education is that the tasks for which it is possible and expedient to use a computer must have a certain structure.

The classical mathematical theory of computation, which for more than half a century remained the philosophical and methodological basis for computational procedures, has now turned into a formalized approximation scheme. The progress of modern computational mathematics is also associated with the intuitive component, more precisely, it depends on the flexibility of mathematical thinking and imagination. However, in a retrospective analysis of mathematical proofs, the formal component, or rather the cognitive power of deductive inferences, creates the illusion of automatic derivation of mathematical proofs, in which each subsequent step inevitably follows from the previous one, providing the conceptualization of new knowledge in an already established system of concepts.

But only some particular processes, and not the whole theory as a whole, lend themselves to computer modeling, since the study of a mathematical model also uses reasoning that does not have a specifically expressed deductive nature. Therefore, the progress of computer mathematics still looks different from the progress of the natural sciences, as well as the social sciences and the humanities, which indirectly affect the public consciousness.

Despite the growing role of computer systems in mathematical cognition, the information model of modern mathematical cognition, partially implemented with the help of a computer or verbalized in a mathematical text, is to a large extent only an "explicit hint" of theoretical knowledge - in contrast to well-formalized mathematical theories, allowing to reconstruct the architecture of the modeled knowledge. From the point of view of the sociocultural philosophy of mathematics, the presentation of mathematics in accordance with a strict axiomatic approach is historically associated with the emergence of theoretical geometry and the mechanism of the formation of the deductive method. The development of mathematical culture occurs not in the process of natural evolution, as, for example, in nature, but as a result of the conscious efforts of mathematicians. Therefore, the philosophical criticism of the idea of ​​the cumulative development of modern mathematics, as well as the rapid change in computer technology and the associated crisis in the ideas of mathematical education can be considered as prerequisite signs of the transition of mathematics to a new quality.

The main feature of mathematics is that it develops somewhat autonomously, since, as a living organism, it is similar to self-regulating systems. This, in turn, contributes to the process of self-justification of the mathematical theory, bringing the meaningful theory to logical perfection in a finite number of steps, a sufficient sign of which is the stabilization of its axiomatic foundation. With regard to structurally complex self-justifying systems, philosophical categories of part and whole acquire new characteristics. The specific direction of the substantiation of the mathematical theory fixes that the part inside the whole and outside it has different properties.

The holistic concept of modern computer education is also not limited to the properties of its parts, although it is characterized by their properties. Therefore, there is a methodological need to take into account the systemic quality of the whole. Just as, for example, in mathematical proof, the methodological conjugation of the whole and the part is essentially connected with persuasiveness and visibility. “If persuasiveness is, to a certain extent, the feasibility of a proof as a whole, completed, but in which the initial and concluding points are especially highlighted,” says the philosopher of science A.N. Kochergin , “visibility is the feasibility of a proof at each point of the chain of evidence without revealing contradictions in the whole, violating the feasibility of the proof as a whole” [2. S. 75].

The duality of these important concepts is manifested primarily in the fact that persuasiveness in a certain sense reflects the visibility of the whole, and visibility can also be interpreted as the persuasiveness of the parts that make up the proof.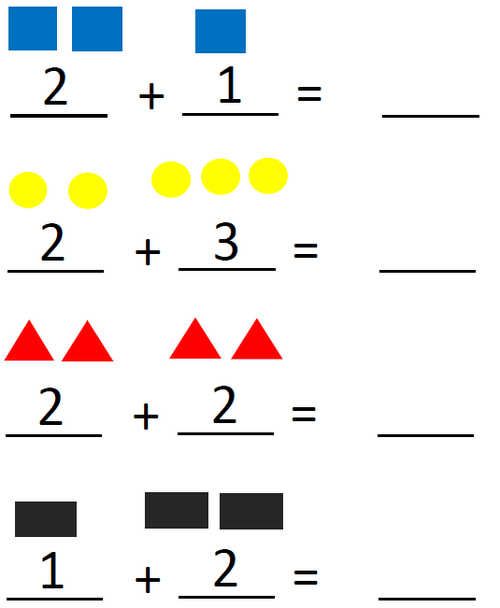

Quantum computer

The formalization of the mathematical proof is still a necessary simplifying procedure that makes the mathematical proof more universal and accessible to the computer. With the help of a computer, you can find options for solving mathematical problems if it is used not only as a computing device for the conceptual enrichment of thinking, but also as a tool that allows you to change stereotypes in the assimilation of mathematical knowledge and in mental activity itself.

In this connection, the outstanding German mathematician David Hilbert wondered whether it is possible in principle to replace the mathematical style of thinking with some kind of automatic process imitating mechanical thinking. In a more precise formulation, it was about whether there is such a universal method by which it would be possible to prove the truth or falsity of any mathematical statement. In the philosophy of mathematics this question has been reformulated.

In the new interpretation, it no longer consisted in proving the truth, but in connection with the development of computer technology in proving solvability. This issue was successfully dealt with by the English engineer and mathematician Alan Turing , whose bold idea was to invent a mechanical device that is actually an analogue of a typewriter, namely: a paper punched tape with symbolic logic. To solve abstract logical problems, he proposed a hypothetical machine to determine which mathematical problems are solvable and which are not, which led to an instrumental revolution in the performance of complex mathematical calculations on real machines.

It should be noted that until the end of the XIX century. complex calculations were considered a purely mental process. The problem that Turing was investigating does not depend on a particular program to justify mathematics in terms of the chosen system of axioms. He was interested in the problem, which in the modern methodological interpretation can be formulated as follows: is there a certain universal mechanical procedure that allows, in principle, to solve all mathematical problems of a certain class?

When a mathematician in difficult situations wants to make sure that a mathematical result is correct, he does not formalize its proof, i.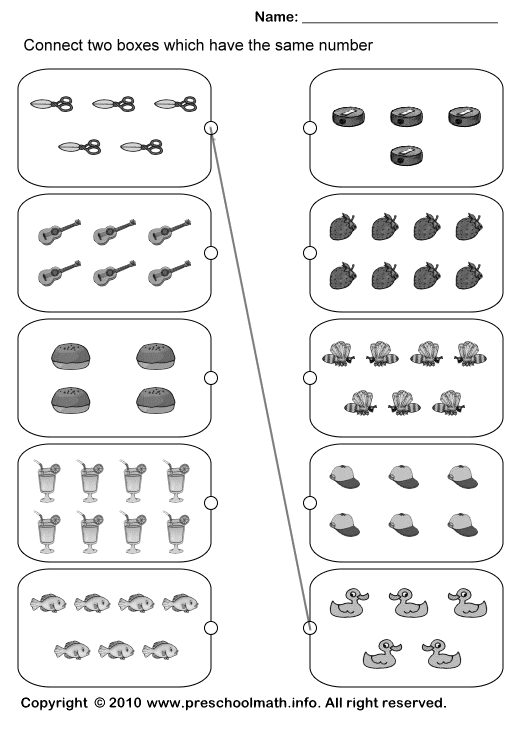 e. does not compare its steps with formal rules, but tries to make it understandable. Believing in the practical reliability of ordinary mathematics, he relies not on logical, but on mathematical foundations. Alan Turing grasped a certain connection between the problem of solvability and the idea of ​​computability. The relevance of the notion of computability, introduced in the 20th century, lies in the fact that “since electronic computers have now become quite familiar to us, it will apparently be sufficient to refer to the operation of these physical devices, and not to the corresponding ideas expressed in the form of strict mathematical formulations. Roughly speaking, - explains the famous mathematician Roger Penrose , a computation (or algorithm) is what some ideal computer does; the word "ideal" means that the computer can work for an arbitrarily long time "without wear and tear", never makes mistakes and has an unlimited supply of memory" [3. S. 324].

This required a simple and accurate model of the calculation process. Mathematically, such a computing device is the so-called "Turing machine", which just met these requirements. In the methodological context, of particular interest are the proofs of mathematical statements, which can be classified as boundless when they reveal new knowledge, but it turns out to be “impossible” to double-check the correctness of the proof, i.e. repeat this process in humans.

In the modern philosophy of computer mathematics, which synthesizes both formalist and constructivist problems of the foundation of mathematics, it is very important to have at least a theoretical possibility to establish exactly the moment when the Turing machine will stop. Turing himself showed that there is in fact no algorithmic procedure for mechanically solving the general halting problem. To this we can add that, in contrast to the classical computer, it is generally impossible to define the subject of a quantum computer. Essentially, a quantum computer is a new cognitive theoretical tool.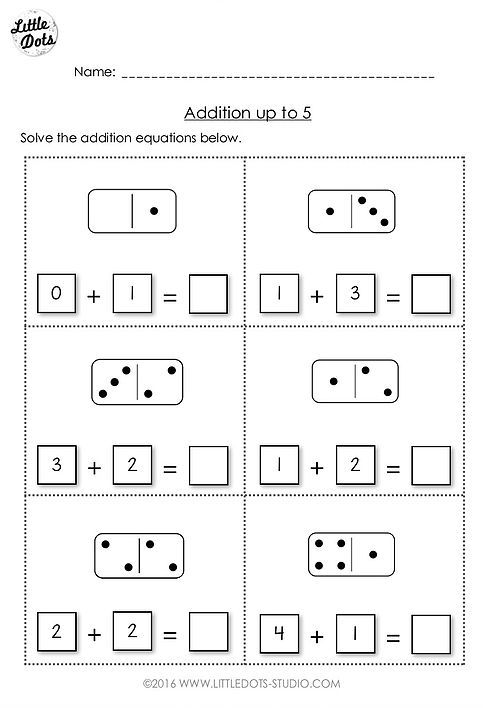 But there are still philosophical questions, the solution of which requires a deeper insight into its essence.

The need for the development of quantum computing in connection with the large information capacity of quantum systems was pointed out back in the 1980s. famous mathematician Yu.I. Manin using unitary transformations in the Hilbert space. This problem was successfully solved by an American specialist in quantum theory and one of the authors of the first quantum algorithm David Deutsch , who formulated the theory of a quantum computer in terms of the Hilbert space, which made it possible to describe the fast counting mechanism, which is inaccessible to classical computing devices [1].

The methodological difficulty of this problem was that it was not enough just to characterize the evolution of a quantum mechanical system, it was necessary to present a more serious proof of its implementation.

In 1985, David Deutsch theoretically proved that in quantum physics there is a so-called "universal quantum computer" capable of performing any calculation that any other quantum computer can perform. “All I had to do,” explained the scientist, “is to copy Turing devices; but to determine the physics underlying them, use not classical mechanics, which Turing implicitly accepted, but quantum theory” [4. S. 213]. In essence, all modern computers, using both traditionally mechanical and quantum mechanical processes, in the philosophical and methodological context are different technological implementations of the same classical idea of ​​a universal Turing machine.

This means that even the mathematical processing of information is a complex task, consisting of a variety of methodological approaches and philosophical ideas that cannot be combined in one mathematics program. And this is directly related to Gödel's incompleteness theorems.

Without exaggerating the philosophical role of Godel's incompleteness theorem, we can say that Godel's result says, first of all, that the entire set of arithmetic truths demonstrated as formal mathematical statements cannot be enumerated by a Turing machine. But to focus only on Godel's limitations, without taking into account the experience of research traditions in mathematics, the rich and varied content of which is not limited to abstract set-theoretic mathematics, is to be proud of its philosophical and methodological impotence or the failure of the modern philosophy of mathematics as a science.

Computer proofs

The practical application of a mathematical theory is, as a rule, wider than the solution of the practical problem with which this theory was originally associated.

As for the "world of abstract mathematics", it is, as before, rarely open to direct perception, so it cannot be identified with the "world of conceptual ideas" of reality. The embodiment of an idea into strict mathematical statements with valid deductive conclusions capable of transmitting information in an accessible way requires considerable effort and theoretical capabilities [2].

In the modern theory of creative thinking, it is substantiated that in the process of solving difficult creative problems, “passing through mistakes” is inevitable. The dual nature of the error manifests itself when it is necessary to distinguish formal memorization from conscious understanding. In the practice of mathematical education, the quality of errors is incomparable.

A new philosophical understanding of this problem arose when American mathematicians Kenneth Appel and Wolfgang Haken proposed their own method for solving the "four colors" problem. It consisted in proving that in order to color any conceivable map, provided that no two adjacent regions, i.e. having a common border, did not turn out to be painted in the same color - only four colors are enough [3].

Although this conjecture was proven for some finite number of domains, progress to infinitely many domains was unsuccessful until, in 1976, the problem was solved by a computer, thereby overturning traditional ideas about mathematical proof. But such non-standard peer review was strongly objected to by some leading mathematicians, who considered computer verification inadequate, since it does not guarantee trouble-free operation in the "bowels of the computer" and against corresponding failures in its logic.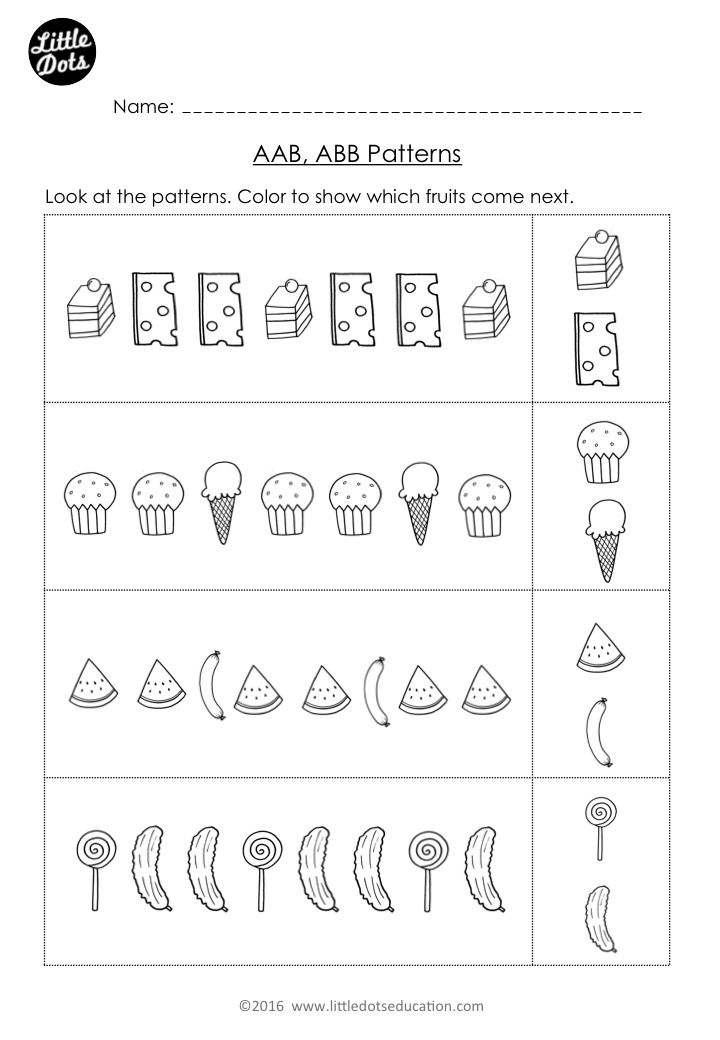 In addition, in the operation of every modern computer, due to its dual structure, namely, possible weaknesses in software or electronic equipment, there may be unnoticed errors[4].

The evidence so far does not clarify this situation, since the critical stage of mathematical proof requires the use of a computer, and its “answer” replaces the identification of mathematically formalized truth.

The essence of this philosophical and methodological objection is as follows. In hard-to-see mathematical reasoning using a computer, one has to translate the relative into the absolute with the help of a finite and strictly indefinite number of checks. Perhaps that is why the justification of the correctness of computer calculations is subject to the same methodological restrictions as the results on the unsolvability of certain mathematical problems, and it is more difficult to justify them, the more efficient the corresponding computer program is.

Nevertheless, the use of "silicon logic" in the future changes the practice of mathematical proof. And although for some mathematicians the proofs of theorems carried out using complex computer programs cannot be considered reliable and are considered as guiding the theoretical search for hypotheses, they can still be considered as a theoretical construct of the prerequisite for developing a new concept of substantiating mathematics, taking into account its practical needs.

Computer evidence marked a fundamentally new stage in understanding the role of computer education and mathematical modeling of processes occurring in the real world. The mathematical model as a "generally recognized canon of representation" of the external world and its conventional nature fix a certain attitude towards the modeled object of the cognizing subject himself.

Even if we assume that intuitive mathematical concepts contain some latent aspects that may not appear for quite a long time in "real mathematical practice", then this is essentially the same mathematical Platonism, considering the world of mathematical objects as independent of the reasoning of mathematicians . The last statement should be treated with some skepticism [5].

Therefore, according to the English mathematician John Barrow , “it is possible that in the future the nature of mathematics will be perceived in a closer association with physically realizable processes, such as calculations” [6. S. 321]. Although the application of this classification outside of mathematics is still not so significant, in mathematics this result has already found applications in various fields. This is one of the most striking and instructive examples of the methodological complexity of the modern problem of understanding mathematical proofs. It can be classified as a crisis, which refers precisely to those mathematical proofs that were carried out using a modern computer.

The corresponding problem can, for example, be formulated as follows: Can a proof be considered mathematical if it is done on a computer?

On the one hand, crises in the philosophy of mathematical knowledge are epistemological in nature and do not seem to be connected with the ontology of mathematics; but, on the other hand, if we consider mathematics as a creative process, it can be structurally likened to a kind of "architecture", as the famous Bourbaki group did . However, then these crises can be interpreted as crises of human thought, when the "architects" of science realized that it was impossible to build a multi-kilometer structure, and therefore it makes no sense to discuss what stability properties they would have.

Regarding the new post-Gödelian crisis associated with the use of computers in theorem proving, we can say that no clarity has yet been brought to this problem, since there are no real technologies for proving the correctness of computer programs. Different philosophical views on the sources of human knowledge, as well as the difficulties of mathematical knowledge based on the ontological unity of sign constructions, led to pluralistic, at first glance, incompatible points of view on the future of mathematics.

Conclusion

In summary, let's pay attention to the interesting philosophical work of the beginning of the new millennium by the English mathematician Brian Davies "Where is mathematics going?". It substantiates the thesis that by the end of the last century, the most exact of the sciences experienced upheavals that could fundamentally change the nature of the results obtained in it. Logical insights Gödel led to 1930s to the first of three crises. But, according to Davis, since the 1970s. two more crises have occurred in modern mathematics, as unpredictable as the crisis caused by Gödel's incompleteness theorem.

“Both of them,” believes B. Davis, “are connected with the problem of overcomplication: the proofs have become so long and complex that no scientist would have taken the liberty of unambiguously confirming or challenging their correctness” [7. S. 1351]. The second crisis relates to the implicit validity of mathematical proofs carried out using modern computer tools. The third crisis of overcomplexity is related to the excessive complexity of the proofs of some famous mathematical problems. Just about them was discussed above.

The solution of a mathematical problem formulated in several sentences can take tens of thousands of pages of mathematical text. How, then, can it be fully understood by a single mathematician, even the most highly qualified?

In the context of substantiating mathematical knowledge, what happens when solving mathematical problems with the help of a computer, one can try to explain at different levels of understanding from the point of view of the implementation of thought processes in terms of modern computer tools. Although the principles of operations carried out through computer programs cannot in themselves be understood and justified only through the "architecture" of modern computer equipment.

Not only a philosophical, but also a purely practical problem is the substantiation of the growth strategy of mathematics, based on the transformation of its historical development.

Under the conditions of cumulative-information “flood”, the mathematical tools used earlier cease to work not because the traditional mathematical disciplines have grown too much, but because there are a lot of new areas of modern computational mathematics. The methodological problems of the constructivist philosophy of mathematics are directly related to the conceptual problems of the development and formation of modern computer mathematics. Therefore, it is impossible to "go in cycles" in the scientific style that declares the desire for progress and hush up difficulties and shortcomings, thereby exacerbating the conceptual contradictions that are an indispensable attribute of any concept of the development of computer education and informatics.

Literature

1. Narinyani A.S. Mathematics XXI is a radical paradigm shift. Model, not Algorithm // Questions of Philosophy. - 2011. - No. 1. - S. 71-82.

2. Kochergin A.N. Machine proof of theorems as an unconventional research program in mathematics // Research programs in modern science. - Novosibirsk: Nauka, 1987. - S. 70–89.

3. Penrose R. The Way to Reality, or the Laws Governing the Universe. Complete guide - M.-Izhevsk: Research Center "Regular and Chaotic Dynamics", 2007. - 912 s.

4. Deutsch D. Structure of reality - M.-Izhevsk: Research Center "Regular and Chaotic Dynamics", 2001. - 400 p.

5. Kudryavtsev L.D. Modern mathematics and its teaching - M .: Nauka, 1985. - 170 p.

6. Barrow D. New theories of everything - Minsk: Potpourri, 2012. - 368 p.

7. Davies B. Whither mathematics? // Notices of the American Mathematical Society. - 2001. - Vol. 52. - No. 11. - P. 1350-1356.

[1] Although quantum computers do not yet exist and it is still unclear when their practically useful designs will appear, he formalized the issue of quantum computing in the framework of modern computing theory, considering the first approximate scheme of a quantum computer. But if we take into account the current trend of creating high-speed computers with more efficient and compact software, then modern information technologies should become universally quantum in this sense, because quantum mechanical processes now dominate in all sufficiently small physical systems.

[2] Let us point out, for example, the phenomenon of the amazing efficiency of applications of modern algebra in solving applied problems of cryptography related to the problem of information security. In a purely logical-formal approach, the number of chains made up of links of the "premise-output" type grows at least exponentially with their length, while those that lead to a solution form an exhaustively small fraction of this number.

[3] Our intuition, unfortunately, says nothing about whether this statement is true or not. Perhaps there is a case when five colors are required. It is no coincidence that this problem remained unresolved for almost 125 years.

[4] A detailed criticism of the idea of ​​proving mathematical theorems using a computer is given in a letter from N.M. Nagorny: “Appel and Haken propose to consider some physical process as an element of proof - the process of computing on a computer that has flown and disappeared without a trace. Even if one can prove that their programs were written correctly, one still cannot be sure that the machine and, in particular, the device that printed the final answer, worked correctly. And suddenly the car gave a "failure"? [5. S. 103]. Therefore, in his opinion, the only thing that follows from the work of Appel and Haken is that the search for counterexamples to the four-color theorem can be considered unpromising. But there is no solution to the problem, from the point of view of the standards of modern mathematics, although the recalculation may well increase confidence, but it cannot transfer the proof from the “probable class” to the “absolutely reliable class”.

[5] For example, a complete proof of the classification of simple finite groups, obtained in the early 1980s, takes about 10-15 thousand journal pages. This work was done by the combined efforts of more than a hundred mathematicians and published in various scientific journals in about 500 articles. However, by any mathematical standards, a proof of 3,000 pages would still be too long and overwhelming.

Vizgin Vl.P. Mathematization of Physics – Department of Philosophy

Often under mathematization of science is understood as “the use of mathematical language not only in physics, but also in other sciences of nature” [1. P. 83], as well as the introduction of mathematical methods in the field, previously very far from their influence economics, medicine, pedagogy, psychology, linguistics and even theory art [2. S. 245]. In this section, we briefly review the mathematization namely physics and related sciences related to exact natural science. In fact, it is in this area that vast material has been accumulated, there is a powerful tradition dating back to antiquity, and a number of fundamental philosophical and methodological problems.

We will understand the mathematization of science as the application mathematics for the theoretical presentation of scientific knowledge. At the same time, speech will go not only about the auxiliary, purely computational aspect, but about such an understanding of the role of mathematics, when it is "the main source of ideas and principles on the basis of which new theories are emerging” [3. P.112].

To a large extent our consideration of the problem of mathematization will be of a historical nature: from antiquity to the present.

First math the concept of nature was created by the Pythagoreans (“all things are numbers”). Plato continued Pythagorean tradition, highlighting geometry (“God is always geometer). Plato's theory of matter is the theory of regular polyhedra. Aristotle did not deny the importance of mathematics in the knowledge of nature, but believed scientific concepts extracted from the real world abstractions that can be useful in describing phenomena. Later, during the Hellenistic period, Euclid created the first axiomatic-deductive system of geometry, which became the basis of mathematization ancient optics, statics and hydrostatics (Euclid and Archimedes) and astronomy (Ptolemy). However, the geometry of the "Beginnings" Euclid itself was a physical theory, since it was considered creators as a result of the study of real space. But already in the works Archimedes on the theory of leverage and swimming bodies geometry is used as a finished mathematical structure. Essentially, from Archimedes the Pythagorean maxim "everything there is a number" is replaced by “everything is geometry” [4]. The ancient heritage was preserved and multiplied (in in terms of mathematization of scientific knowledge) by Arab scientists and medieval thinkers. R. Bacon, for example, believed that all sciences should be based on maths. The most impressive achievement of the mathematical approach to astronomy was the heliocentric system of N. Copernicus. In modern times and luminaries exact natural science (I. Kepler, G. Galileo, H. Huygens, I. Newton), and philosophers (F. Bacon, R. Descartes, G.W. Leibniz) considered mathematics (geometry) to be the “prototype of the world” (cf. Leibniz: “Cum Deus calculat, fit Mundus”, i.e. “As God calculates, so the world and does"). However, the development of mechanics and hydrostatics in the XVI century. (especially S. Stevin) and in the XVII century. (G. Galileo and B. Pascal) demonstrates preservation of the Archimedean type of mathematization: Euclidean geometry continues remain the defining mathematical structure.

Newton in "Mathematical principles of natural philosophy" spoke of "the subordination of phenomena to the laws mathematics", and although he used the language of geometry, to formulate the laws mechanics he had to create differential and integral calculus. First carried out breakthrough beyond Euclidean geometry as the mathematical structure of physics: through the efforts of Newton, Leibniz, K. Maclaurin, L. Euler, classical mechanics appeared as theory of ordinary differential equations of the 2nd order. At the same time, the most important stimulating role in the emergence and the development of mathematical analysis and the theory of differential equations played problems of classical mechanics.

Later identified and other mathematical representations mechanics who laid the foundation for the phenomenon of analytical mechanics (J.L. Lagrange), aimed at studying the mathematical structures of the classical mechanics [5]. It turned out that it can be formulated as a calculus of variations (Euler, Lagrange, W.R. Hamilton, K.G. Jacobi, M.V. Ostrogradsky), as a theory differential equations with partial derivatives of the 1st order (Hamilton, Jacobi, S. Lee) as a Riemannian geometry (Jacobi, R. Lipschitz, G. Darboux, G. Hertz), as a symplectic geometry (Lagrange, Hamilton, Ostrogradsky, Lee). These identifications had a decisive influence on the development of mathematics in 19th century and identified structural and mathematical power of classical mechanics (in accordance with "mathematical" criterion for the effectiveness of the research program by I. Lakatos, the power of the program is determined by the degree of its influence on the development of mathematics; this the criterion is related to the criterion of the "good" theory of R. Feynman, according to to which the quality of a theory is determined by the possibility of its presentation in the language of various mathematical formalisms). Lagrangian, Hamiltonian and other formalisms of analytical mechanics discovered amazing vitality, having played an important role in the creation of quantum and relativistic theories of the twentieth century. By the way, analytical mechanics became the first model mathematical physics, which, unlike theoretical physics, at the forefront puts the study of the mathematical structures of physics.

Classic mechanical the program (and the corresponding picture of the world) discovered the method described above mathematization of exact natural science, which, despite the significant the number of adherents from P.S. Laplace to G. Helmholtz and J. Maxwell, turned out to be very limited. Physics (as the science of light, heat, electricity and magnetism), which, with a few exceptions, until the beginning of the 19th century. had no theoretical design, similar to classical mechanics, required the involvement of a new type mathematization. The decisive turn was the intensive use mathematical analysis to represent elementary phenomenological relations in a theoretical form that is not reducible to classical mechanics. On this path to 1st quarter XIX in. were created (mainly by the efforts of French scientists S.D. Poisson, J.B. Fourier, A.M.Ampera, O.Fresnel, S.Carnot and others) mathematical electrostatics, theory thermal conductivity, elements of thermodynamics, electrodynamics, wave optics [6].

In the 1860s - 1870s the creation of classical physics, coupled with its mathematization, was mainly completed (Maxwell's electromagnetic field theory, W. Thomson's thermodynamics and R. Clausius, fundamentals of statistical mechanics of Maxwell and L. Boltzmann). Mathematical analysis and, above all, theory differential equations with partial derivatives of the 2nd order, remained the basic mathematical structure of classical physics. But, at the same time, important additional tools for its mathematization have become vector calculus and probability theory. In crystallography, the theory has been applied groups. By the end of XIX in. revealed a fundamental feature of the basic differential equations classical physics - their variational structure, i.e. the possibility of obtaining based on the calculus of variations (of the variational principles, primarily Hamilton's principle). Looking ahead, we emphasize that the fundamental differential equations of motion (field) appearing in quantum mechanics, general theory of relativity, quantum field theory and elementary particles (i. e. equations of Schrödinger, Einstein, Dirac, etc.), as it turned out later, are also derivable from the variational principle. Variation of the basic equations physics makes it possible to relate the basic conservation laws with symmetries (groups invariance), corresponding theories in the spirit of the famous theorem of E. Noether [7,8].

Mathematization of others natural sciences was carried out through physics and classical mechanics (celestial mechanics, astrophysics, some branches of chemistry, etc.). A. Poincare on at the turn of the 19th and 20th centuries. connected the mathematical-analytical (i.e., based on mathematical analysis and differential equations) the nature of classical physics with its locality and homogeneity. As a result, knowledge of an elementary fact made it possible to obtain description of the process by means of differential equations, the integration of which led to the description of many observed phenomena. The absence in biology of characteristic for the physics of locality, homogeneity, simple elementary relations, according to Poincare, prevented the mathematization of biological sciences [6].

Scientific revolution, occurred in physics in the first third of the twentieth century, significantly changed the relationship between physics and mathematics. In addition, mathematics played a significant role in this revolution itself [9]. First of all, at construction of the theory of relativity, especially general, and quantum mechanics in full to a lesser extent, the leading role of mathematics was manifested. Unlike the classics, in which mathematics (differential equations) was preceded by the establishment of a connection between physical concepts and mathematical quantities, in the development of relativistic and quantum theories the search for an adequate mathematical structure was ahead of its physical comprehension. So, when creating the general theory of relativity, it was first found Riemannian structure of space-time and tensor-geometric concept gravity, and only after that the actual physical side was clarified affairs. When creating quantum mechanics, the mathematical foundations of the theory (for example, the Schrödinger equation for the wave function, the physical meaning of which remained unclear) and only after that the physical interpretation of the theory was developed (probabilistic interpretation of the wave function, the principles of uncertainty and additionality). It is these achievements theoretical physics allowed to talk about "pre-established harmony" between mathematics and physics (G. Minkowski, F. Klein, D. Hilbert, A. Einstein and etc.) [10], or about “the incomprehensible effectiveness of mathematics in the natural sciences” (E. Wigner) [11]. To some extent, it looked like a revival of the Pythagorean-Platonic the concept of mathematization of scientific knowledge or its more modern version in spirit of Kepler, Newton and Leibniz.

If classical physics looked from a mathematical point of view primarily as a theory of differential equations with partial derivatives of the 2nd order and, accordingly, the mathematical-analytical structure was decisive, then in non-classical science to the fore advanced the theory of transformation groups and their invariants, differential-geometric structures and functional analysis. Important importance was also retained by the theory of differential equations and the calculus of variations, with the help of which the laws of motion were formulated, as well as the theory of probability, which allows correctly formulate the concept of a state in the statistical and quantum mechanics. The invariant-theoretic approach, which became after the creation of a special theory of relativity as a powerful and universal means of constructing a theory, meant the spread "Erlangen program" F. Klein on physics, in other words, led to understanding scientific theories, first of all, as theories of invariants of some underlying fundamental symmetry groups [12]. General relativity led for the first time to the geometrization of physical interaction (namely, gravity) in the language of the theory of Riemannian curved spaces. Transition from classical to quantum corresponded to the transition to an infinite-dimensional Hilbert state space and self-adjoint operators, i.e. transition from conventional analysis to functional analysis. Further development in the 2nd half of the twentieth century. put into circulation such sections as the geometry of fiber spaces, topology, infinite-dimensional Lie algebras, etc.

Intensive Triumphs mathematization in the creation of non-classical physics led to such an understanding of the role mathematics, when it is considered not only as a means of quantitative description of phenomena, but also as a generator of fundamental physical concepts and theoretical constructions. Until now, hopes for a breakthrough in fundamental physics theorists associate with the search for mathematical structures, mathematical images, previously not associated with reality (Yu.I. Manin and others) [13]. Essentially, this close to the method of mathematical hypothesis, whose importance in non-classical physics was emphasized by S.I. Vavilov [fourteen].

Despite the steady tradition to consider the above-mentioned "pre-established harmony" as a creed theorists, or the key "empirical law of epistemology", and therefore avoid searching for the foundations of this harmony, there are several promising approaches to its explanation (interpretation).

First - historical and scientific - based on relay model development of physics (natural science) and mathematics D. Hilbert, according to which this efficiency is based “on… the recurring and changing play between thinking and experience” [15.C.17]; on the fact that mathematical concepts in their origins date back to the outside world, physical reality, developing then relatively autonomously into powerful abstract theories, which in turn turn out to be surprisingly suitable for describing new layers of natural science, as if returning his debt [12]. There is an approach based on a reasonable remark about a certain relationship (or even coincidence) of some basic methodological principles of physics and mathematics (N.F. Ovchinnikov and others) [one]. Such, for example, are the principles of symmetry (invariance), saving, matching, etc. In the "preinstalled harmony" between physics and mathematics, of course, there is an aesthetic moment. Sometimes they even think that it is expedient to introduce the concept of "mathematical beauty" of physical theories and that this harmony is connected with him (P. Dirac, S. Weinberg and others) [16,17]. During the process of mathematics a kind of "natural selection" of effective structures, and it is with them that associated with the concept of mathematical beauty. This selection may be related the desire of theorists to choose problems that have "beautiful solutions". The very concept or feeling, "mathematical beauty" evolved from the regularities of whole numbers and regular polyhedra to Euclidean geometry and from it to mathematical analysis and differential equations, and then from them to the theory groups, differential-geometric structures and functional analysis. There are also attempts to link "pre-established harmony" between physics and mathematics with the structure of our brain, with the physical and mathematical nature of our thinking (consciousness) (R. Penrose, J.P. Change and others) [18,19].

Of course possible reassessment of the mathematical principle in the development of scientific theories, when hopes on the "mathematical solution" of scientific problems are not justified. That's how it happened for example, when trying to build a unified field theory based on using more general geometries than Riemannian. Despite the elegant and powerful geometric methods, due to lack of physical grounds for the geometrization of the electromagnetic field, these attempts were unsuccessful [twenty].

fear the so-called "Pythagorean syndrome" (an expression by R.A. Aronov), interpreted as unjustified identification of mathematical forms and theoretical structures with forms and structures of the objective world [21,22]. Justification for such identification is the success of the theory (this was the case when creating a general theory relativity and quantum mechanics). If identification does not lead to success, the corresponding mathematical hypothesis is discarded. However, mathematical structures that have not justified themselves at this stage can be not only valuable for mathematics, but also be useful in subsequent development physical theory. Those for example, turned out to be geometry Weyl and the five-dimensional generalization of Riemannian geometry, which did not lead to a successful solution of the problem of a unified field theory, but became sources of such important physical concepts like gauge interpretation of the field and the idea of ​​a multidimensional space [20].

Scientific and technical revolution of the 1940s-1960s, or the transition to "big science" associated with the development of nuclear energy and outer space, the creation of computers, lasers, etc., led to a new wave of mathematization of natural and technical sciences, which, in turn, made a significant contribution to this revolution. The key achievement here was the creation electronic digital machines (computers) and the concept of computing experiments that radically expanded the scope of mathematization, including in its scope not only the tasks of management and economics, but partly also the humanities.

At the intersection of various sciences in 2nd half of the twentieth century. formed a new synthetic direction of the mathematization of science, called synergetics or non-linear dynamics, in which non-linear tasks, processes of self-organization and stochastic dynamics. On the one hand, within this direction managed to solve a number of important problems of physics and technology, as well as to mathematize important branches of chemistry, biology and social sciences. On the other hand, this led to new impulses for the development of mathematics (nonlinear differential equations, fractal geometry, theory of singularities of differentiable mappings and etc.) [23].

Mathematics physics is often accompanied by the reverse process - the physicalization of mathematics. it expressed, on the one hand, in the richness and fruitfulness of mathematical concepts generated by physics (V.I. Arnold et al.) [24]. On the other hand, theoretical physics sometimes prompts mathematicians to transform even Foundations of Mathematics (Jet Nestruev, A.M. Vinogradov) [25].

Mathematization of scientific knowledge is introduced into the methodology and philosophy of science. interesting and important an example of this kind is the approach of L.D. Faddeev to one of the fundamental methodological principles of physics - the principle of correspondence, as well as the concept scientific revolution. Using the language of mathematical deformation theory algebraic structures, which, in particular, are the fundamental groups physical theories (say, the Galileo-Newton groups and the Poincaré group), and the transitions considering them as deformations, he comes to the conclusion that the transition from classics to non-classics, or "the two main revolutions in physics . .. from the point of view of mathematics are deformations unstable structures into stable ones” [26.С.15]. At the same time, under a stable, according to L.D. Faddeev, one should understand such a structure, all close deformations of which are equivalent to her. From this point of view, classical mechanics is "doubly unstable" - by the constants of the speed of light and Planck, which in this case are parameters deformations.

The issue of whether to consider mathematization one from the methodological principles of physics (N.F. Ovchinnikov, I.A. Akchurin), along with principles of symmetry, correspondence, etc. [1,27], or consider it as a separate common feature of the theorization of scientific knowledge [28]. Regardless of the answer to this question should be recognized that mathematization has always been and continues to be remain the main and most effective means of theorizing scientific knowledge, whose development has a powerful impact on mathematics. Wherein we have to admit that the problem of mathematization of science belongs to number of the most important problems in the methodology of science that require further research.

In conclusion, I would like to without cluttering the section with additional references, among the important works on problem under consideration, in addition to those already cited, to mention the works I.S. Alekseeva, S.V. Illarionov, S.V. Kotina, A.A. Pechenkina, E.M. Chudinova, different time working or working and now at the Department of Philosophy of the Moscow Institute of Physics and Technology.

List of sources

Akchurin I.A. Mathematization as a principle of unity of physical theories // Methodological principles of physics / Ed. ed. N.F. Ovchinnikov and B.M. Kedrov. M.: The science. 1975. P.204–224.

Arnold V.I. Mathematics and Physics: Parent and Child or Sister // Uspekhi physical sciences. 1999. No. 12. pp.1311–1323.

Aronov R.A. Pythagorean Syndrome in Science and Philosophy // Questions of Philosophy. 1996, No. 4. pp.134–146.

Bazhenov L.B. etc. Philosophy of natural sciences. Issue 1. M.: Ed. polit. lit. 1966.

Vavilov S.I. Old and new physics // History and methodology of natural Sciences. Issue III. Physics. M.: Ed. Moscow State University. 1965. pp. 3–12.

Weinberg S. Dreams of final theory: physics in search of the most fundamental laws of nature. M.: URSS, 2004.

Wigner E . Studies on symmetry. M.: Mir, 1971.

Vizgin V.P. "Erlangen program" and physics. M.: Science. 1975 (see also: Vizgin V.P. "Erlangen program" by F. Klein and physics // Uchenye zapiski Academy of Education. 1998. Issue 2. pp.46–63).

Vizgin V.P. Unified theories in the first third of the twentieth century. M.: Science. 1985.

Vizgin V.P. Between mathematics and physics: an ongoing discussion // Historical and mathematical research. Second series. Issue 5 (4)). Moscow: Janus-K. 2000. pp. 361–369.

Vizgin V.P. Development of interrelation of conservation principles in classical physics. M.: Science. 1977.

Vizgin Vl.P. "Doctrine of Faith" theoretical physics: "pre-established harmony between pure mathematics and physics" // The problem of knowledge in the history of science and culture. Rep. ed. E.N. Molodtsova. St. Petersburg: Aletheia. 2001. pp. 123–141.

Vizgin Vl.P. Mathematics in the quantum-relativistic revolution // Physics XIX–XX centuries in general scientific and sociocultural contexts: Physics of the XX century. Moscow: Janus-K. 1997. pp.7–30.

Vizgin Vl.P . Mathematics in classical physics // Physics of the 19th–20th centuries in general scientific and sociocultural contexts: physics of the 19th century. M.: Nauka, 1995, p.6–72;

Vizgin Vl.P. Between mechanics and mathematics: analytical mechanics as factor in the development of mathematics (XIX century).// Studies in the history of physics and mechanics. 1986. M.: Nauka. 1986. pp. 49–62.

Vizgin Vl.P. Reflections on the methodological principles of physics // Philosophy science in a historical context. Collection of articles in honor of the 85th anniversary of N.F. Ovchinnikov. St. Petersburg: RKHGI; ID.SPbGU.2003. p.293–311.

Hilbert D. Mathematical problems // Sat. "Hilbert's Problems". Ed. P.S. Alexandrova. M.: Science. 1969. P.11–64.

Dyson F. Mathematics in the physical sciences // Mathematics in the modern world / Ed. V.A.Uspensky/. M.: Mir. 1967. pp. 111–128

Dirac P. Principles of quantum mechanics. Moscow: Nauka, 1979.

Dirac P. Evolution of the physical picture of nature // Elementary particles. Above what physicists think. Moscow: Fizmatgiz. 1965. Issue 3. pp. 123–139.

Manin Yu.I. Mathematics and Physics. M.: Knowledge, 1979.

Nestruev Jet. Smooth manifolds and observables. M.: MTSNMO.2000.

Ovchinnikov N.F. Principles of theorizing knowledge. Moscow: Agro-print. 1996.

Penrose R, Shimoni A, Cartwright N, Hawking. Big, small and human mind. M.: Mir. 2004.

Pogrebyssky I.B. Mathematical Structures and Physical Theories (From Archimedes to Lagrange) // Questions of the history of natural science and technology.

Learn more

• 
  About rhyming words
• 
  Abc songs for children sesame street
• 
  Short stories for kid
• 
  Learn shapes preschool
• 
  What are the dra levels
• 
  Short stories for kid
• 
  Learn shapes preschool
• 
  What are the dra levels
• 
  What is guided reading level
• 
  The color brown song
• 
  Math problem for first graders