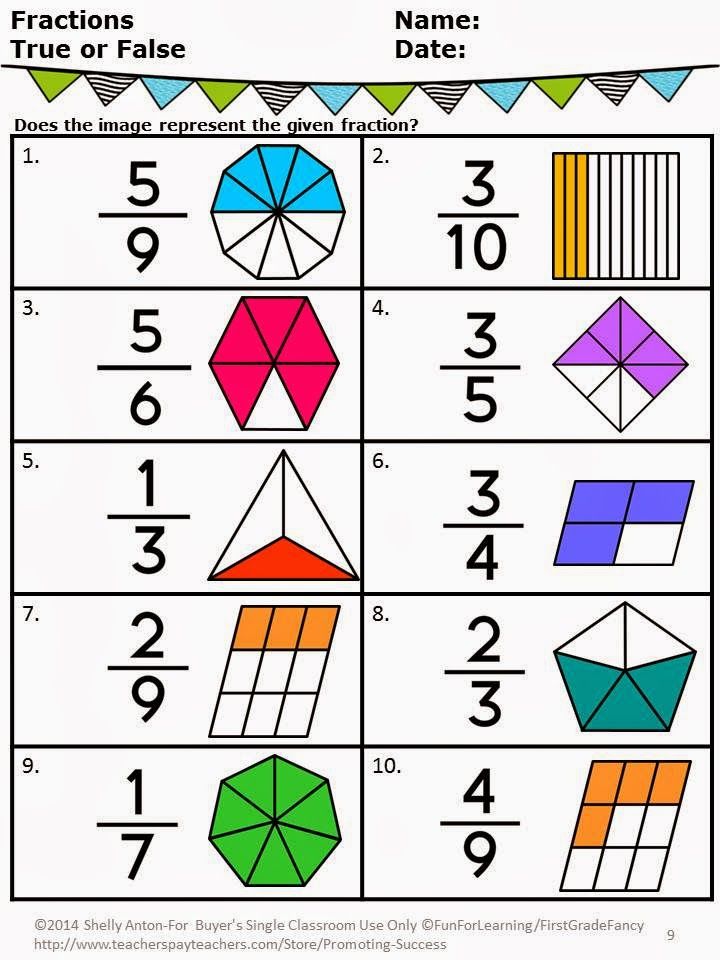
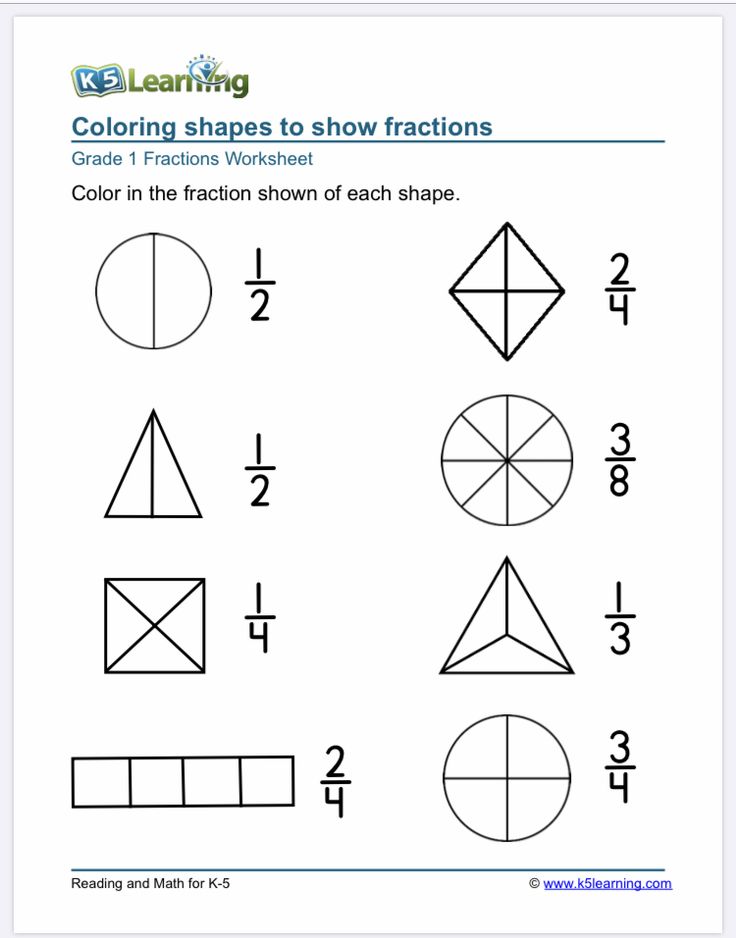
Teaching 1st grade fractions

Miss Giraffe's Class: Fractions in First Grade

I know I seem to say this about every math concept I blog about but I LOVE FRACTIONS.

Well, the first grade version of fractions :)

It's weird to even hear myself say it because I struggled, and I mean struggled, with fractions in school. I was a good test taker though so I always flew under the radar with my teachers but I remember just looking at them like What is this?!

SO I think it is really important to build those fraction foundations so your students don't end up staring at fractions the way I did!

I think the first concept in fractions to teach is EQUAL PARTS, or EQUAL SHARES.

See those funky shapes with unequal parts on the right?? We call those "nutty shapes"!

Our job is to help our squirrel friend find the nutty shapes with unequal parts so we sorted the shapes by whether they had equal parts or unequal parts.

Then some practice!

Once your students understand that fractions have equal parts, I recommend having them partition fractions themselves! The most fun way to do this, in my opinion, is with dough!

In small groups, give each student a ball of dough. Provide a rolling pin for them to roll their balls flat and some circle cookie cutters to cut out circles. If you don't have rolling pins, you can use pretty much anything - even a highlighter - or they can just smash it down with their hands. If you don't have circle cookie cutters, you can use anything with a circle base. Turn a plastic cup upside down and press it in. Can you tell I improvise a lot?? :)

This activity is not only super fun but it promotes SO much good conversation and thinking.

Guide your students by having them cut one of their circles in half. Talk about how each of the 2 shares is a half and together they're called halves. Then have them cut their other circle into half.. and then half again. Let them know these are called fourths because there are four equal parts. As they're looking at their halves and fourths side by side, ask them if they notice anything. Discuss how the more shares you cut it into, the smaller the shares get. You could also cut your circle in an unequal way and ask if it's cut into halves/fourths/whatever and help them see that the shares must be equal to be called halves/fourths/etc.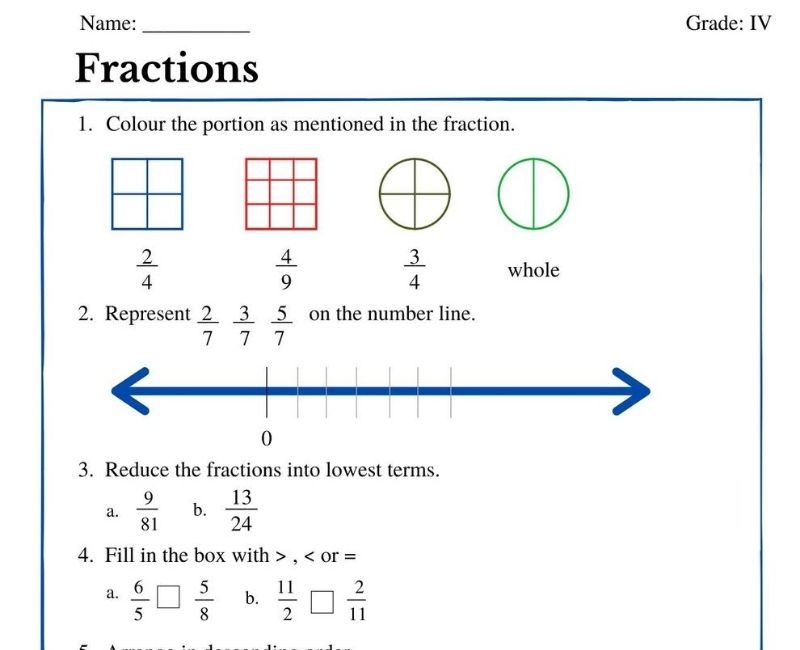 There are so many great concepts you can teach with the dough out! I also made a cute little recording sheet to go along with it so they can write about what they learned during/after their exploration.

For more halves, fourths, etc. practice, I made practice sheets in different difficulty levels.

One of the types of worksheets I made were these sheets that focus on a specific type of fraction (cut into halves, thirds, fourths, or eighths).

I love these because they practice several skills at once but for each type of fraction so it's not too confusing or overwhelming.

If you need something a little easier, this is a great worksheet to do first to review what halves, thirds, and fourths are:

And of course some cutting and pasting action because I love having them for every math concept ever because kids love it and it is great, self-checking practice.

I've said this before but...

According to 5 and 6 years olds:

Math Worksheet = Math.

Math Worksheet + Cutting/Gluing = Party.

and a little coloring action too because who doesn't love coloring?!

Once you think they've got it down, I recommend busting out the Fraction Flowers!!

I included this activity in a bunch of different ways because I love it so much. You can use it as a craft, a math puzzle/center, or hang the flowers up as a poster or visual aid.

The craft makes a super duper cute bulletin board!

I love the way ours turned out! Sorry for the #notsohumblebrag but I can't help it - I love, love them and they were a lot of fun to make!

Can someone help me think of a cute bulletin board title? "Come see what we're growing in our Fraction Garden!" "Our Fraction Garden is Blooming" ... I can't figure out exactly what I want it to say :)

For this math craft, we sorted the HALF OF fractions and FOURTH OF fractions. I also include WHOLE, THIRD OF, and EIGHTH OF.

It's differentiated as well so you can choose how much to challenge your students. Each flower comes in both full color and black & white.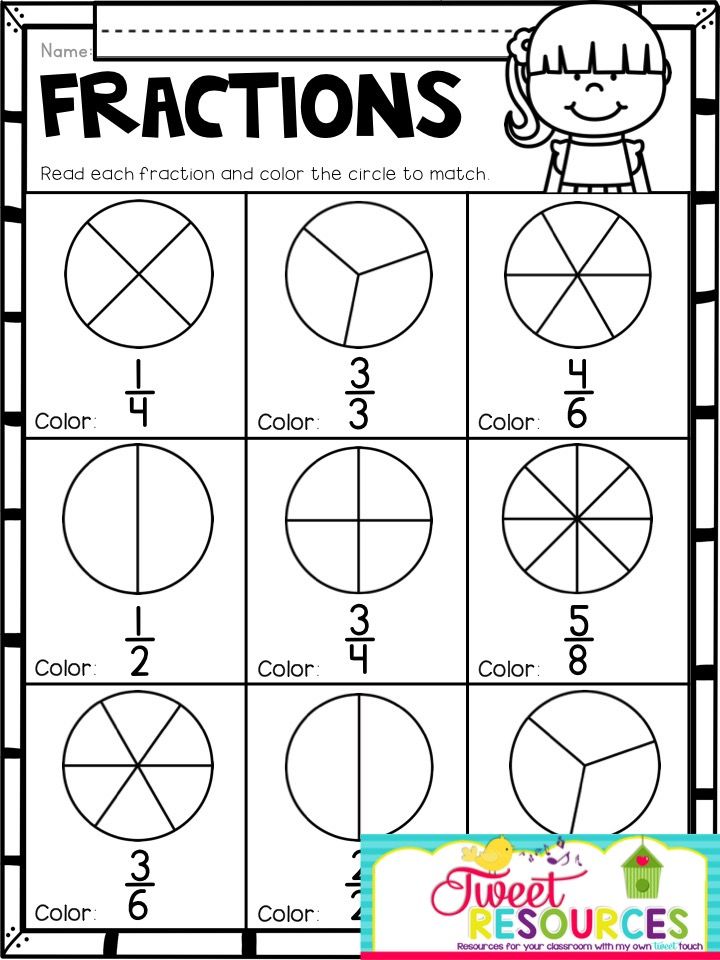 Each of those options also comes in pre-made (where the flower is already put together as a pretty flower like you see above) OR mixed up in pieces for students to sort and build their own flowers.

For the craft, I just printed the premade black and white flowers so all you had to do is color in the fraction either half of or fourth of, color the rest of your flower, and then cut and glue it to the construction paper.

What I recommend if your students are up for the challenge (or you have a select few that are) and you have the time, have them sort the petals to the right flower first! It's an awesome sorting activity that adds even more learning to the craft. Print the 'mixed up in pieces' black and white version for students to SORT FIRST to build their flowers. They'll put the petals with the right flowers and arrange them to build their flowers. It might not be as "perfect" looking for your bulletin board as the above example but it'll be authentic and awesome! (I used to always want bulletin boards to be perfect examples of perfect work and I finally realized that was silly and it was the imperfections and differences that made them authentic and beautiful examples of work - random weird philosophical thought, sorry! :))

The mixed up pieces color version is a review center for next week!

Students sort the petals to the right fraction and then copy what they match onto their recording sheet.

For the premade color ones, I printed and laminated them to use as a visual.

Right now, they're on my table as a reference tool but I'm going to cut them out and hang them up as a classroom poster display soon.

Being able to partition the fractions into halves and fourths themselves is a big concept in first grade so that's important to practice! I made worksheets to practice but this one (the easy level - A) is good to throw in a pocket protector with dry erase markers to practice in small groups when introducing it. Encourage your kiddos to find multiple ways to divide the circle/square into halves/fourths/thirds/whatever.

Once you feel like they really get the fundamental concepts, you can move into the number representation of fractions. I know a lot of first grade teachers are told not to do it but I personally think that once you lay down the basics, they're very capable. If you're saying "1 out of 3" shares, they might as well know the representation.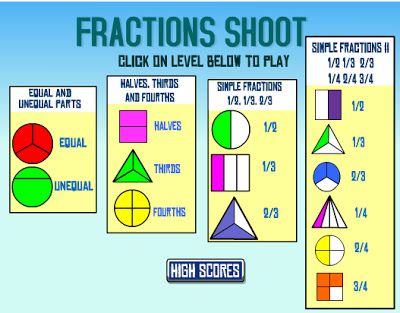 BUT if you disagree, that's fine! I created some very simple straightforward worksheets and centers to practice it for those who want to venture into the fraction abyss.

I think a great way to help kids understand it is to write "out of" on the line that separates the numerator and denominator and teach them to read down to "read" the fraction. It really helps them get what the fraction means, but most importantly, they won't mix up the numerator and denominator if they know what the written expression for the fraction actually means. For example, the circle has 3 out of 4 pieces colored so that is how they would read it starting at the 3 and going down: "3 out of 4". Here is what I mean:

Puzzles obviously because I would make puzzles of puzzles if I could :)

And what else?? Cut and pasting fun! Always <3

Thank you for listening to me share some of my ideas for teaching fractions. I hope you got some new ideas!

If you want the activities from this post, they're ALL included in my:

First Grade Math Unit 18

along with A LOT more worksheets, centers, cutting and pasting activities, and assessments!

Unit 18 is also included in the First Grade Math Units 10-18 Bundle if you want all of the second half of my first grade math units :)

Okay one more thing I want to share with you that I love. ....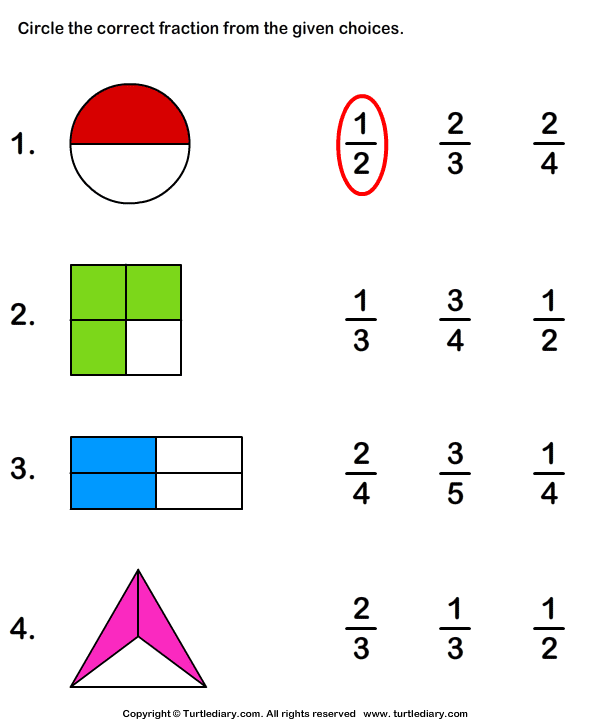

FRACTION BOWLING!!!

I scored this adorable little bowling set at Target for only $7 over the weekend and I'm so excited to use it. You can find 10-piece bowling sets in a lot of places so if you can't find this at Target, I'm sure you can find one online pretty easily. It comes with 10 plastic bowling pins and 2 little plastic balls.

So the way to play Fraction Bowling is to set up all the pins. (It comes with a mat that shows exactly where to set the pins to make it easy for kids to set up but I set it up without it because it's cuter for the picture, not gonna lie :))

Have students take turns rolling the ball to the pins to try and knock them down. I recommend letting them roll it twice just like with regular bowling so they don't completely miss on their turn and get upset. There are 2 balls.. an orange ball and a purple ball so they could get both balls to start and roll each.

At the end of their turn, they go to their recording sheet and color in how many pins they knocked down out of the 10 pins on the worksheet. Then, they write the fraction they made. So if they knocked down 4 pins, they'd color in 4 of the pins on their recording sheet and write 4/10 next to it. You can skip the writing the fraction part if your kids aren't ready for it. Just the 4 out of 10 is great practice anyway! Or if you want to make it harder for your super high kids, make them make a fraction of ALL the pins once they're all done (ex: 36/60 pins total).

I made a simple little recording sheet to go with it that you can download for free by clicking here:
Fractions Bowling
:)

If you want to save these ideas for later on Pinterest, feel free to pin this or any other picture from this post:

Fractions for First Graders - Firstgraderoundup

We've been tackling ~FRACTIONS~ the last two weeks in first grade! I used to dread teaching fractions to 6 year old littles, but thanks to some extra CGI training on fractions...I love it!

The biggest ah-ha I've learned over the years is that fractions and shapes go together. They are all under the umbrella of "geometry." Having math talks about shapes bleeds over into conversations about fractions and vice versa!

We spent the first week talking about the difference between "whole" and "half."

The first day, I posed a CGI problem...

"Mrs. Shaddock has 1 cookie to give to 2 first graders. How much cookie can each friend have to get a fair share?"

I love starting with this problem because it sets kids up for a problem....what are they going to call that part of the cookie? In my experience, most firsties can tell, show or act out the fact that it's a half of a cookie...but not as many know how to label it. I got a wide variety of answers once again this year...

*1 piece

*1 cookie

*2 cookies

*half

We shared many of these and talked about the fact that if I just say "1" or "1 piece" I don't know how much that is. When I just say "1" I'm assuming a whole cookie...If I told you I would give you one cookie, but I only gave you one small piece, you would be upset because you assumed I would give you the WHOLE cookie!

Then, we start our whole/part anchor chart. ..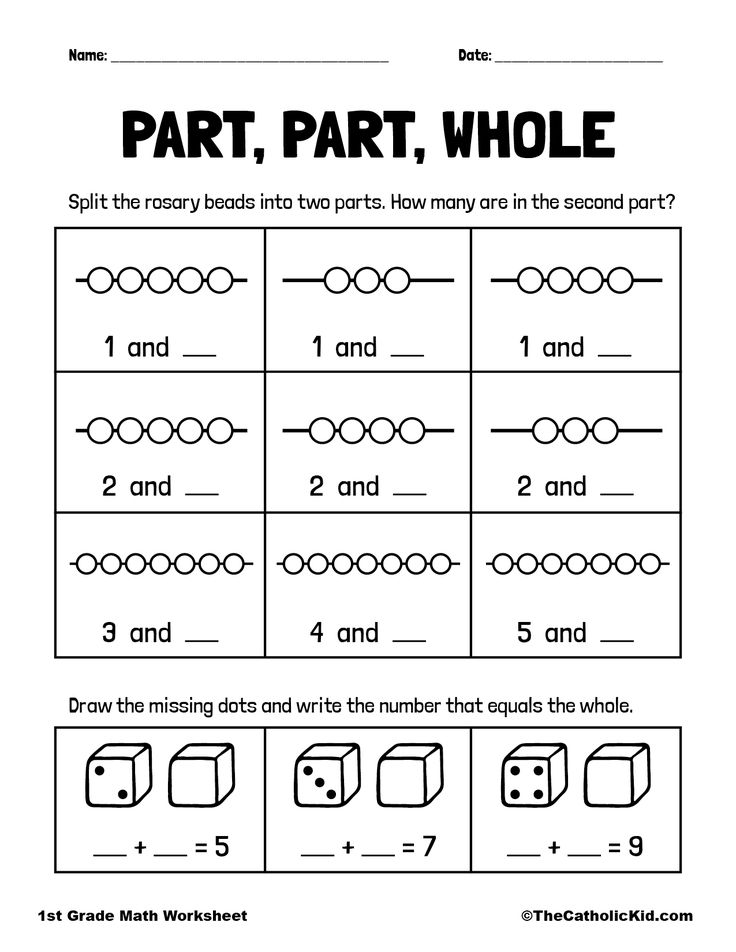

Of course, we didn't add the fourths until the second week. Also, notice the emphasis on this anchor chart on "whole" and "part." We worked on fraction CGI problems these weeks, but also some part part whole CGI problems and we were able to make some really great connections between these problems and fractions during our share time that made fractions easier to understand!

The next day, we did a few math talks about which shapes were divided in half using the math talk slides from my geometry packet...Then, the next morning, the kids did this sort for morning work (halves/not halves the first week and fourths/not fourths the next week)....

On the last "math skill" day of the week, we played "Pass the Pen," which happens to be the simplest game and one of my first graders' favorites....

Get this:
*Share the paper between your table group and choose a "pen" (or pencil or crayon) to share between your table group.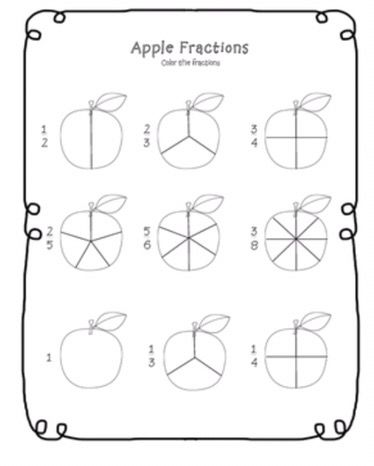
*One person starts and divides a shape in half/fourth.
*Then, they....wait for it...pass the pen...to the next person at the table who has to divide another shape in half/fourths a different or new way.
*They keep passing the pen until they cannot think of any more new ways.

It's definitely not rocket science, but they love it! And this game is so good to use in pretty much any subject area!

If a kid doesn't know what to do, they other friends at the table can help him/her and tell her what to do, but can't do it for him....

We did one round of the squares and then shared pictures and talked about if they were halves/fourths and why or why not. We talked a lot about being precise and how that affects the partitioning. And for whatever reason, squiggly lines were quite popular this year, so we had to talk about that too!

Once we discussed the squares they flipped their paper to the other side and played the same game with circles.

At the end of the activity, I had them pass the pen to assess the squares together and then self-assess the circles as a group. Love these smiley face grades! :)

Fractions came after all of our 2D and 3D shape exploration in geometry, and our next step will be symmetry...but that will probably be after Christmas break! We are about to be in full on assessment mode in my world! #keepinitreal

Grab these activities and more in my complete geometry packet!

How to explain actions with fractions to a child

Fractions are one of the most difficult but important topics in mathematics. It can be difficult for an unprepared student to study it and perform various actions, but with the right approach, the most difficult sections of exact science become understandable and accessible. To study the topic of fractions, you need to use fantasy, imagination and convey the material in a game format. In order for the student to be able to independently complete the tasks, the teacher will need time and patience.

The term "fraction" means division. As part of the school curriculum, the study of this topic begins in high school, but teachers recommend starting its development at preschool age. Getting basic knowledge about fractions allows you to train counting skills, concentration, logical and spatial thinking.

How to start learning fractions for children

You should start studying the topic with the concept of "shares". To do this, you can use illustrative examples - divide a dish or object into equal parts, explaining what a half, a third and a quarter are. A good exercise would be building a construction set, where children can divide the whole into parts, memorize the same cubes and count different elements. The more shares obtained by dividing, the less they will be. The child should be aware of the usefulness and relevance of fractions in everyday life. When he understands this, the process of understanding the topic will be easier and faster.

The fraction is not an integer. To record the required number of shares, the concept of an ordinary fraction is used. It consists of two indicators: the denominator and the numerator, which are separated by an oblique or horizontal line. The numerator is indicated above the fractional bar, and the denominator is written below and indicates the number of parts from the whole.

Types of fractions: regular and improper fractions

There are regular and improper ordinary fractions. Correct fractions are those in which the numerator is less than the denominator (3/4). In improper fractions, the value of the numerator is greater than the denominator, and the whole part (6/4) can be distinguished in them. The numerator is divided by the denominator, resulting in an integer part and a remainder. Improper fractions also include those in which the numerator and denominator are equal (10/10). The constituent parts of such a fraction are converted into a unit.

Mixed numbers can be converted to improper fractions.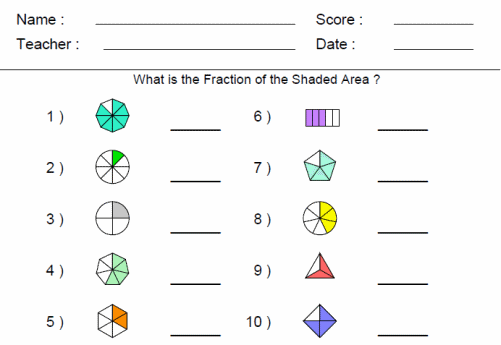 To do this, you need to multiply the part of the whole by the denominator, and add the numerator to the resulting amount. To simplify fractions, it is necessary to reduce. If both parts of a fraction are equal, then they can be divided by a single number. When adding ordinary fractions, the denominator remains unchanged, and the numerators are added. If the denominators are different, then the least common multiple must be determined. Fractions are subtracted in the same way. To multiply ordinary fractions, you need to consistently multiply the denominators and numerators together. When dividing fractions, multiply the numerator of the first by the denominator of the second and vice versa. When comparing fractions, you need to pay attention to the numerator: the one with its value will be larger. With the same numerators, the larger fraction will be the one whose denominator is smaller. If, when comparing, one of the fractions is incorrect, then it automatically becomes larger. These mathematical operations often cause difficulties for children, so you need to understand them in practice.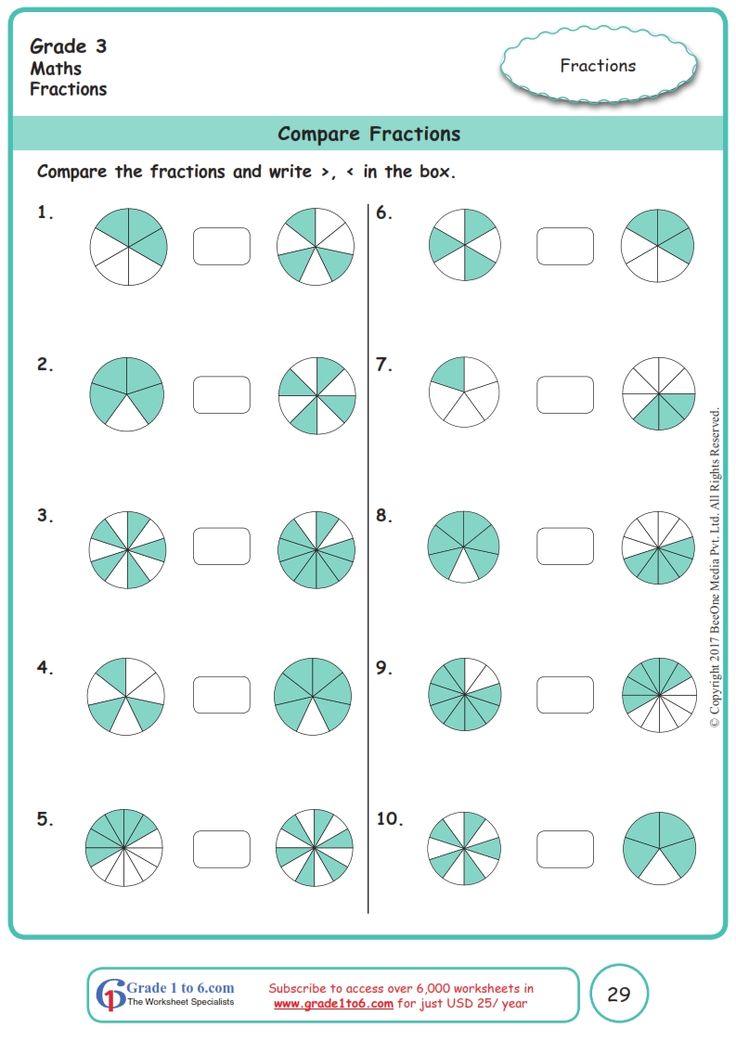

If the denominator of a fraction contains numbers that are multiples of ten, then they are respectively called decimal. Pupils write down the indicator of the whole, separating the tenth parts (5.2) with a comma. In mathematics, there are also fractions without a whole value. To do this, write down zero and after the decimal point indicate the value of the numerator (0.05). Decimals are especially useful for precise calculations. Such a system has long proved its practicality, it is simple and understandable for students.

When children need to learn fractions

In order for the study of the topic of fractions and their place in mathematics to be productive, it is necessary to carefully analyze each action with teachers, consolidating the acquired knowledge and skills in practice. Teaching mathematics online develops the ability to analyze, think critically and draw conclusions, perceive and process information, generalize and systematize knowledge. The remote format of classes allows you to acquire skills at a convenient pace and comfortable conditions, and the results will be noticeable after the first lessons. The sooner children get acquainted with the concept of fractions, the easier it will be for them to write them down and perform mathematical operations in the future.

Teaching Fractions at AMAkids School

The AMAkids Academy for the Development of Child Intelligence provides online mathematics education for children from the age of six. The staff of the educational organization employs qualified teachers with extensive experience who can find an individual approach to each child. Classes are held on a special interactive platform with the use of electronic manuals and game simulators. Teachers convey the material not in the form of standard lectures, but in the process of an exciting game, guided by the author's methodology.

Mathematics online from the AMAkids Academy consists of several blocks: arithmetic, geometry, basic programming and financial literacy. In arithmetic classes, children learn measures of quantities, get acquainted with the concepts of integers and ordinary fractions, learn to perform simple numerical operations.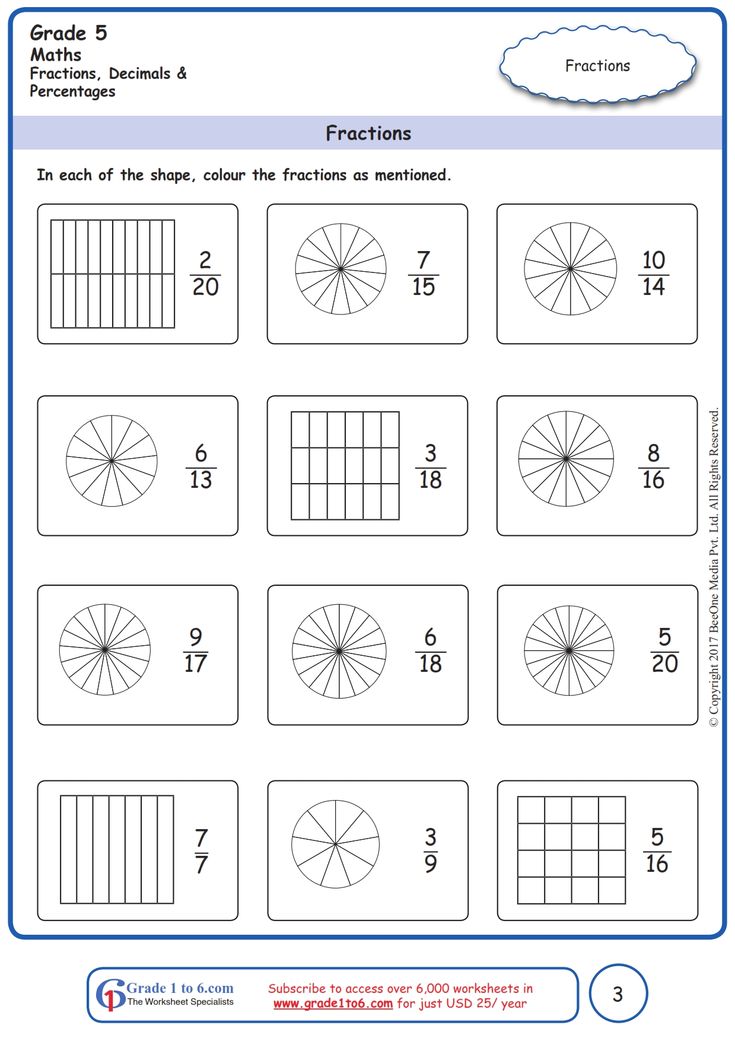 In geometry lessons, students get acquainted with the basic geometric shapes and their characteristic features, explore the concepts of area and perimeter, symmetry and asymmetry.

Financial literacy includes the study of financial security, the concepts of price and value, get acquainted with the history of the monetary system. Students will learn how to make purchases correctly and with maximum benefit. On the basis of programming, children will learn about algorithms and sets. Children solve logical problems and examples of different levels of complexity, perform tasks for the development of memory and voluntary attention.

Construction of a mathematics lesson in the 5th grade on the topic “Ordinary fractions” (to the textbook by S.M. Nikolsky and others)

Construction of a mathematics lesson in the 5th grade on the topic “Ordinary fractions” (to the textbook by S.M. Nikolsky, etc.)

Voronova Svetlana Nikolaevna, mathematics teacher

Sections: Mathematics, School Library Organization

“The only way leading to knowledge is activity”.
B. Shaw

It is the system-activity approach is a feature of the new standard generations in teaching as a GEF methodology. New students receive knowledge not in finished form, but are obtained in the course of educational research under teacher guidance. Learning activities becomes a source of internal development schoolchild, the formation of his creative abilities and personal qualities.

many different approaches and trends. TO These include teaching strategies, under which are understood as goals, distribution of roles and choice of means teaching at a particular stage educational process.

For constructing a math lesson in grade 5 on the topic “Comparison of fractions” is used Interactive Teacher Interaction Strategy and students. This strategy allows for transition from the one-sided influence of the teacher on students to their direct interaction. The focus shifts from lecture methods of teaching for discussion, and the educational process is built in a dialogue mode. Teaching acquires an individual character. Students have the opportunity receive answers to their questions and offer your own solutions. Formulation Topics and issues also occur during the discussion. Questions that are raised when studying the or another topic, are the result of a joint activities of teachers and students.

At different stages of the lesson, different technological methods.

At the stage “Problematization, updating, motivation” used reception “Unannounced topic”, which allows to attract students' interest in the study of a new topic, without obstructing the perception of incomprehensible terms.
At the stages “Initial familiarization” and “Feedback: diagnostics, control, self- and mutual evaluation, formative evaluation, reflection” uses a technique from development technology critical thinking called “Before and after". This approach develops the ability predict events, ability to correlate known and unknown facts, to express their thoughts, compare and draw a conclusion. In the table from two columns, the "Before" part is filled in, in in which the student writes down their guesses about the topic of the lesson, about solving the problem, can write down hypothesis. The "After" part is filled in at the end lesson when new material is learned.
At the stage “Rehearsal and consolidation” “Catch the mistake” and “Cluster” techniques are used. Reception "Catch the mistake" forms the skill analyze information, apply knowledge in non-standard situation, critically evaluate received information. The teacher offers students information containing unknown number of mistakes. Students looking for a mistake in a group or individually, confer, accept solution. Next, the representative of the group sends the results to the teacher or announce them in front of everyone class.

Cluster reception is a graphic organization of the material, revealing the meaning of that or some other concept. The key concept is written in the center of the sheet, arrow-rays depart from it in different sides and connect it with other words, from which, in turn, the rays diverge further.

At the final stage of the lesson, the student compares the contents of the "Before" table and "After" and concludes.

Technological map of the math lesson at 5 class on the topic “Comparison of fractions” is given in Appendix 1.

Literature.

I. Mushtavinskaya, O. Krylova. New didactics modern lesson in the context of the introduction of Federal State Educational Standards LLC. Toolkit. – M.: KARO. 2015.
E. Ivanshina, O. Ivashedkina. Modern pedagogical technologies. methodical allowance. – M.: KARO. 2015.
Zagashev I.O., Zair-Bek S.I. Critical thinking. Critical thinking: development technology.
Learn more