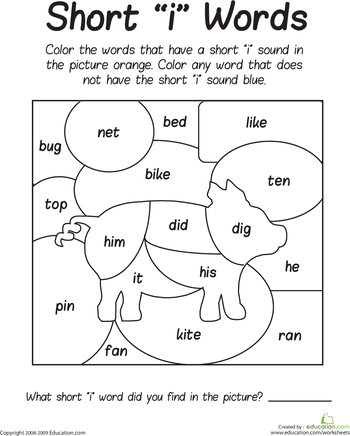
Home » Misc » Teaching letter recognition

Teaching letter recognition


How To Help Your Child Learn The Alphabet

One of the first steps your child will take on their reading journey is learning to recognize letters. Before your young learner can start to sound out words, blend syllables together, or master other early reading foundations, they’ll need letter recognition skills.

Maybe you’re just getting started with letter recognition (or looking for some new ideas) and wondering about the best ways to practice with your child. Good news: HOMER is here to help!

Letter Recognition: Beginnings

When helping your child learn to recognize letters, it’s good to remember that all children have unique personalities, which means they have unique learning styles, too. This will help you and your child feel confident with their reading and learning development!

That being said, many children may express an interest in learning the alphabet by age two or three. This can manifest in a few different ways. If they have older siblings, your child may ask for “homework” to do while their siblings do theirs.

Around this age, your child may also notice the people around them reading books that look different than theirs. Instead of pictures, these books have lots of words. Your toddler may want to know how to read those “big” books, too!

Since your child likely isn’t enrolled in any sort of formal schooling yet, their initial interest in reading and letter recognition may be light and casual. This is great! There’s no need to rush into it.

But if you want to expand your child’s letter recognition skills or engage their interest more purposefully, stay tuned for tips on how to help your child learn the alphabet!

Tips For Encouraging Letter Recognition

Prioritizing letter recognition activities that are fun, simple, and engaging for your child is a great way to help them practice consistently and effectively.

There are many ways to introduce the alphabet to your child and help them learn letters or build their alphabetic skills if they’ve already started recognizing letters. Here are some fun and easy ideas you can try from the comfort of your own home!

Read Alphabet Books

Although this technique may seem simple and common, it’s common for a reason — because it’s effective! And, as a bonus, you likely have several alphabet books around your home already.

Repeated exposure to the alphabet sets a strong foundation for your child to develop their letter recognition skills. Starting with the basics is essential to preparing them for more reading activities as they grow and develop.

Once your child is introduced to the basics, they can move on to more advanced beginning reading activities.

Touch And Feel Letters

Kids spend all day touching and exploring the world around them. Teaching your child letter sounds can be easier (and more fun for them!) when you engage skills that aren’t just visual or auditory.

Plus, let’s be honest — kids love to get messy! Letting them make a mess with letters offers them a great incentive to learn.

We recommend using anything you have around the house that is malleable enough to turn into letters. Shaving cream, pipe cleaners, PlayDoh, and popsicle sticks are all great options.

Play with your child as they build letters out of these materials (or swipe their fingers through a big pile of shaving cream!). If you want to go mess-free, you can also cut out letters from textured paper (like sandpaper).

Here’s how this method works:

  • First, introduce the letter to your child. Trace or make the letter in whatever material you choose.
  • Next, establish an association for your child. Ask your child to follow along while you draw the letter.
  • Once your child has mastered following along with you, you can engage their recall skills. Draw a letter and ask them which one it is.

This activity might take a bit of time and practice, but don’t worry! You and your child will get there.



Explore Names Together

This activity can be effective and useful for helping your child learn letter recognition as well as the names of people on their sports teams, in their school classroom, or any other group of people.

If you want to try this with your child, write down a list of the names of the people in the group you’re focusing on. If it’s your first time doing this activity, consider starting with just your child’s immediate family to make it a bit easier.

Print the names on a large sheet of paper in a dark, easily readable color. Then ask your child to identify letters by saying something like, “Which name has an O in it?”

Change up the letter in question until you cover each name, and then help them tally up all of the letters they find!

To amp up the fun, make a game of seeing which letter appears the most times. You can even make bets beforehand (we suggest banking on a vowel). Whoever guesses which letter will appear most often gets a reward!

This activity helps reinforce two ideas to your child: first, it engages their letter recognition skills by exposing them to the alphabet repetitively.

Secondly, it helps them understand that the alphabet is a code made up of symbols (letters).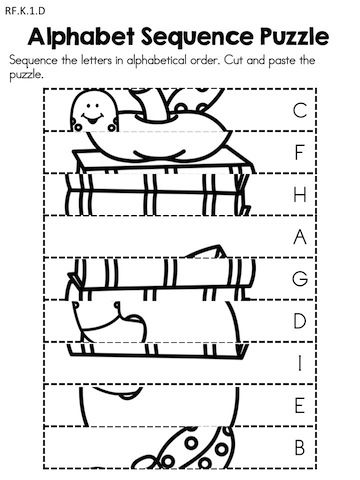 In order to learn how to read, they must learn how to recognize their letters first!

Create A Personalized Set Of Alphabet Cards

Similar to alphabet books, alphabet cards are an easy, reliable option to help your child learn letter recognition. And while there are many alphabet cards on the market, it’s way more fun to let your child make their own!

If you want to try this activity with your young learner, all you need are some large index cards (blank sheets of paper will work if you don’t have index cards) and lots of fun, decorative materials and supplies (glitter is our personal favorite)!

Simply have your child write one letter on each card and then color and decorate it. For younger children, you can also write the letter for them and let them spruce it up to their heart’s content!

This activity is amazing because it allows your child to make their learning highly personal and tailored to their specific interests.

By creating their own cards, your child will be able to exert some autonomy and independence over their learning goals. It may help them become even more invested in their journey toward letter recognition!

Fill In The Dots

One challenge for children when it comes to recognizing letters is understanding what shapes letters are “made” of.

For example, the letter O is often taught as a letter that looks like a circle. Other letters are made up of curves, straight lines, dashes, and all sorts of shapes!

A helpful option for supporting your child’s efforts to recognize their letters is to break down the shapes that make up letters. This is where dot markers (or round stickers) can come in handy!

By utilizing a uniform shape — like a dot — to work through the alphabet, your child can begin to grasp the shape of letters both visually and physically. Understanding how letters are formed can help kids recognize letters more readily.

There are many free downloadable “dot letter” worksheets online that you can use for this exercise. But if you want to create them on your own, simply write out the alphabet in a large script, using empty circles to form the letters.

Your child can then follow along with stickers or dot markers and fill in the empty circles.

Letter Recognition As A Strong Foundation

At the end of the day, practicing letter recognition with your child is all about setting up a strong, solid foundation they can use to launch the rest of their reading and learning journey!

We hope these suggestions come in handy for helping to develop your child’s letter recognition skills. As your emerging reader learns to recognize letters, remember that every child is unique. What works for one may not work for another.

For those days when you need a little extra help, our online learning center is the perfect place to find safe, personalized, and effective activities for your child. Try our free onboarding quiz to get started!

Author

14 Letter Recognition Activities for Preschoolers

  • Share
  • Email

Helping preschoolers to gain letter recognition skills does not need to feel like “work. ”

The best way to teach letter recognition is through play, in a fun, stress-free, and positive manner. 

Here’s a brief intro to letter recognition, followed by 14 letter identifying activities.

What Letter Recognition Means

Learning letter recognition skills involves several different hands-on components. 

Children need to distinguish the shapes of letters from each other (visually recognize them) and be able to point to and state the letter names, as well as the sounds made by each letter.

In addition, they must learn to form letters and write them. 

These skills do not all need to be accomplished during the preschool years and in fact, preschoolers are not yet developmentally ready to learn to read and write. 

By simply exposing children in a fun way, you will begin the process of laying down foundational pre-reading and writing skills.

When Should a Child Recognize Letters of the Alphabet?

Although you can read about average ages when kids gain alphabet skills, those often vary widely.  

Just as children learn to walk and talk at different ages, the same is true for recognizing letters of the alphabet. 

They each learn at their own pace, depending on many factors. 

How to Build Skills to Prepare Children for Letter Recognition

Through fun play activities, parents can help their children gain various developmental skills that prepare preschoolers for letter identification. 

Those types of skills include visual perception, memory and auditory perception.

What this means is that learning the letters does not in fact start with exposure to the actual letters, but rather to play activities that develop these skills.

Visual Perception

Visual perception refers to a child’s brain making sense of what their eyes are seeing, such as details and shapes (shape recognition). 

These skills also include visual-motor and eye-hand coordination. 

Helpful kinds of activities include:

  • Those that exercise the large muscles (such as throwing/catching).
  • Small motor activities (like lacing).
  • Visual perception (such as building puzzles).
  • Limiting screen time, which has limitations related to visual perception skills.

Memory

Memory development relates to storing and using information in the brain. 

Stress-free activities to enhance these skills include:

  • Simple card games
  • Memory card games (get your own by downloading the FREE set of printables at the end of the post)
  • Talking about fun memories
  • Story visualization
  • Reading and talking about books
  • Visual memory games, like picture bingo
  • Auditory memory games 

Auditory Perception

Auditory perception includes the brain’s ability to distinguish sounds and words, which is important for learning the sounds of letters. 

These are the kind of activities that can support this skill:

  • Listening to music
  • Distinguishing animal sounds
  • Clapping out copied rhythm patterns 

[source]

How to Teach Letter Recognition to Children

Even before children show an interest in print, these kinds of activities are meaningful and fun and will set the stage for letter recognition:

  • Reading to them
  • Sharing poems and nursery rhymes
  • Talking to them
  • Telling stories
  • Singing songs to or with them

Keep it fresh, keep it new, and be willing to return to their favourite activities when asked.  

As your children show a growing interest in print, make it available to them whenever possible.

Instead of keeping that book to yourself as you read to them, show children the words, running your fingers over them as you read. Let kids turn the pages of books. 

Have books available in the home to which kids have constant access. 

So many things around the house contain words, like packages, lists, letters, emails, screens, magazines, and greeting cards. 

Point and touch as you read, showing children that you are using words daily, expressing how much can be learned through their use. 

Write in front of your kids for all different purposes, at least sometimes spelling aloud. 

Make drawing and writing tools and surfaces available to children at all times, indoors and out. 

Don’t just offer the traditional papers and crayons – include:

  • Drawing with sticks in the sand
  • Writing on clay or playdough
  • Drawing on shower and bath walls with soap 

Should I Teach the Letters in a Specific Order?

Instead of teaching letters in any special, prescribed order, focus on those that are used most often and in order of importance for your children.  

They typically want to know about the letters:

  • In their names.
  • In “MOM” and “DAD”.
  • In a pet’s name.
  • In environmental print (like on STOP or WALK signs).
  • In outstanding words from a favourite storybook.

Think about and pay attention to those letters and words that appear to be interesting to your kids, using them as the foundation to build upon.

Then, when children are ready to formally learn the letters, teach them using sets of letters that make the most combinations of words, as explained in this article on teaching letters.

Is it Better to Teach Upper or Lowercase Letters First?

For preschoolers, the field of occupational therapy makes a good case for beginning with capitals in handwriting letter formation. 

They are formed from larger lines and curves that avoid retracing and changing directions, while still teaching top to bottom strokes. 

If children try to form letters for which their visual-motor skills are not prepared, they sometimes build poor habits that can be difficult to break later on.  

Of course, your children may be familiar with lowercase letters, seeing them in many print formats, and gradually learning to identify them. 

When their motor skills are ready, they typically make an easy switch to including them along with uppercase when they write. 

 [source] 

Letter Recognition Activities and Games for Preschoolers

Here are some fun ways to teach letter recognition through play. 

1. Point Out Environmental Print

Print is all around us. 

Point out, talk about and stress the sounds of words on signs (such as favourite restaurants and traffic/street signs), cereal or other product boxes/labels, and familiar logos. 

2. Share Rhyming Books

Read favourite rhyming books to your children, accentuating the rhyme and rhythm. 

Afterwards, play an oral game of stating some rhyming words from the story and adding a new rhyming word of your own. 

Challenge your kids to come up with more words that rhyme. Either real or pretend “words” are okay, as it is the rhyming factor that counts. 

3. Letter Hunt

Point out and talk about the letters in your child’s name, making them clearly visible in print.

Show them how you find one of those same letters in a magazine or newspaper and cut it out as a rather square piece (not necessarily trying to cut out close to the letter’s edges). 

Challenge them to find other letters from their name in print and cut those out, as well. 

After all the letters have been found, they can arrange them in the correct order for their name. 

These may be kept in a small bag for future use or glued onto a coloured sheet of paper to post on the fridge or in your child’s room. 

Instead of cutting, another option is to use different colours of highlighters to mark various letters found in print. 

4. Play with Plastic/Wooden Letters

Letters may be sorted and put into piles in different ways: 

  • Those with curves
  • Letters with straight lines
  • Those from a child’s name or other important words
  • Letters they can name
  • Those for which they can say the sounds

Letters with magnets may be used on the fridge or on a magnet board for sorting purposes.

5. Bake Letters

Use bread or pretzel dough to form letters with your children, then bake them to be eaten later.

While you work, talk about the letter names, sounds, and easy words (like their names) that may be formed. 

Special baking tins and cookie cutters may be purchased to bake letters. You can also bake oblong cakes and cut them into large letter shapes, as well.

6. Form Letters with Familiar Materials

Offer kids various types and colours of pasta to form letters on flat backgrounds, either to glue into place or to leave loose and rearrange into different letters. 

Other materials to explore might include:

  • Dry breakfast cereals
  • Buttons or pennies
  • Cotton balls
  • Dried beans
  • Mini-marshmallows
  • Toothpicks
  • Rice
  • Yarn

7. Form Letters with Unusual Materials

Using a tabletop or oblong baking pan with low sides, spread shaving cream or pudding for children to trace letters into with their fingers.  

The same may be done with sand (or moved outside), to trace in with fingers or safe “sticks,” like pencils, dowels, or rulers. 

8. Go on a Scavenger Hunt

Have children choose a letter card or cutout. Talk about how the letter looks and sounds. 

Depending on children’s level of development, challenge them to find things around the house that have that letter printed on them or objects that begin with that letter’s sound. 

9. Fish for Letters

Magnetic letter fishing games may be purchased or made with paper, magnets, paper clips, dowels, and string. 

Name or pick a letter, focusing on how it looks and/or sounds. Kids then “fish” for the matching letters from the “pond.” 

They can also just fish for a random letter and then name it once it is “caught.” 

You can also use a version of this game later on, when children are learning to match upper and lowercase letters.

10. Play Musical Chairs with Letters

Add paper plates with letters or letters cut from cardboard right onto the chairs or onto the floor beneath.  

Children walk around the circle and find a place to sit when the music stops. They each then name the letter on their chair or floor directly beneath.

11. Find Letters on a Keyboard

Make use of an old computer keyboard or typewriter. Get kids to name the letters as they touch the keys. 

They can also find them to press as you say the names, sounds, or hold up cards, one letter at a time. 

12. Spray or Write Letters Outdoors

Offer spray bottles with water for children to spray letters on driveways, sidewalks, or even the side of your house. 

Another option is to use sidewalk chalk to write letters on the driveway, patio, or basketball court. 

13. Form Letters with Bendable Materials

Get your children to bend pipe cleaners, chenille stems, or products like Wikki Stix (string covered in wax) to form letters. 

Children often like to make multiple letters and form words, as well.

14. Find the Hidden Letters

“Bury” plastic or wooden letters in a sand table or sand box. Ask children to name the letters as they are discovered. 

Other materials may be used as alternates in sand tables or large trays, such as coloured rice, pasta, dried beans, or birdseed. 

All of these ideas for teaching letter recognition can help to strengthen a child’s early literacy skills.

Pay attention to where they stand in their development and keep raising the bar just a bit higher, while still returning to those games and activities in which they feel a high measure of success. 

This is the key to learning.

Get FREE access to Printable Puzzles, Stories, Activity Packs and more!

Join Empowered Parents + and you’ll receive a downloadable set of printable puzzles, games and short stories, as well as the Learning Through Play Activity Pack which includes an entire year of activities for 3 to 6-year-olds.
Access is free forever.

Signing up for a free Grow account is fast and easy and will allow you to bookmark articles to read later, on this website as well as many websites worldwide that use Grow.

  • Share
  • Email

do text recognition in half an hour / Sudo Null IT News

Hi Habr.

After experimenting with a well-known database of 60,000 MNIST handwritten digits, a logical question arose whether there is something similar, but with support for not only numbers, but also letters. As it turned out, there is, and such a database is called, as you might guess, Extended MNIST (EMNIST).

If anyone is interested in how this base can be used to make a simple text recognition, welcome under cat.



Note : This is an experimental and educational example, I was just curious to see what happens. I did not plan and do not plan to make a second FineReader, so many things here, of course, are not implemented. Therefore, claims in the style of “why”, “there is already better”, etc., are not accepted. Probably ready-made OCR libraries for Python already exist, but it was interesting to do it yourself. By the way, for those who want to see how the real FineReader was made, there are two articles in their blog on Habré for 2014: 1 and 2 (but of course, without source codes and details, as in any corporate blog). Well, let's get started, everything is open here and everything is open source.

Let's take plain text as an example. Like this:

HELLO WORLD

And let's see what we can do with it.

Breaking text into letters

The first step is to break the text into individual letters. OpenCV is useful for this, or rather its findContours function.

Open the image (cv2.imread), convert it to b/w (cv2.cvtColor + cv2.threshold), slightly enlarge it (cv2.erode) and find the contours. 

 image_file = "text.png" img = cv2.imread(image_file) gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY) img_erode = cv2.erode(thresh, np. ones((3, 3), np.uint8), iterations=1) # Get contours contours, hierarchy = cv2.findContours(img_erode, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE) output = img.copy() for idx, contour in enumerate(contours): (x, y, w, h) = cv2.boundingRect(contour) # print("R", idx, x, y, w, h, cv2.contourArea(contour), hierarchy[0][idx]) # hierarchy[i][0]: the index of the next contour of the same level # hierarchy[i][1]: the index of the previous contour of the same level # hierarchy[i][2]: the index of the first child # hierarchy[i][3]: the index of the parent if hierarchy[0][idx][3] == 0: cv2.rectangle(output, (x, y), (x + w, y + h), (70, 0, 0), 1) cv2.imshow("Input", img) cv2.imshow("Enlarged", img_erode) cv2.imshow("output", output) cv2.waitKey(0)

We get a hierarchical contour tree (parameter cv2.RETR_TREE). The first is the general outline of the picture, then the outlines of the letters, then the internal outlines. We only want the outlines of the letters, so I make sure the "parent" is the overall outline. This is a simplistic approach, and it may not work for real scans, although this is not critical for screenshot recognition.

Result:

The next step is to save each letter, after scaling it to a 28x28 square (this is the format in which the MNIST database is stored). OpenCV is built on top of numpy so we can use array functions for cropping and scaling. 

 def letters_extract(image_file: str, out_size=28) -> List[Any]: img = cv2.imread(image_file) gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY) img_erode = cv2.erode(thresh, np.ones((3, 3), np.uint8), iterations=1) # Get contours contours, hierarchy = cv2.findContours(img_erode, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE) output = img.copy() letters = [] for idx, contour in enumerate(contours): (x, y, w, h) = cv2.boundingRect(contour) # print("R", idx, x, y, w, h, cv2.contourArea(contour), hierarchy[0][idx]) # hierarchy[i][0]: the index of the next contour of the same level # hierarchy[i][1]: the index of the previous contour of the same level # hierarchy[i][2]: the index of the first child # hierarchy[i][3]: the index of the parent if hierarchy[0][idx][3] == 0: cv2. rectangle(output, (x, y), (x + w, y + h), (70, 0, 0), 1) letter_crop = gray[y:y + h, x:x + w] # print(letter_crop. shape) # Resize letter canvas to square size_max = max(w, h) letter_square = 255 * np.ones(shape=[size_max, size_max], dtype=np.uint8) if w > h: # Enlarge image top-bottom # ------ # ====== # ------ y_pos = size_max//2 - h//2 letter_square[y_pos:y_pos + h, 0:w] = letter_crop elif w < h: # Enlarge image left-right # --||-- x_pos = size_max//2 - w//2 letter_square[0:h, x_pos:x_pos + w] = letter_crop else: letter_square = letter_crop # Resize letter to 28x28 and add letter and its X-coordinate letters.append((x, w, cv2.resize(letter_square, (out_size, out_size), interpolation=cv2.INTER_AREA))) # Sort array in place by X-coordinate letters. sort(key=lambda x: x[0], reverse=False) return letters

At the end, we sort the letters by X-coordinate, just as you can see, we save the results as a tuple (x, w, letter) so that we can then extract spaces from the spaces between the letters.

Making sure everything works: 

 cv2.imshow("0", letters[0][2]) cv2.imshow("1", letters[1][2]) cv2.imshow("2", letters[2][2]) cv2.imshow("3", letters[3][2]) cv2.imshow("4", letters[4][2]) cv2.waitKey(0)

The letters are ready for recognition, we will recognize them using a convolutional network - this type of network is well suited for such tasks.

Neural network (CNN) for recognition

The original EMNIST dataset has 62 different symbols (A..Z, 0..9 etc): 

 emnist_labels = [48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122]

The neural network, respectively, has 62 outputs, at the input it will receive images 28x28, after recognizing "1" it will be at the corresponding output of the network.

Creating a network model. 

 from tensorflow import keras from keras.models import Sequential from keras import optimizers from keras.layers import Convolution2D, MaxPooling2D, Dropout, Flatten, Dense, Reshape, LSTM, BatchNormalization from keras.optimizers import SGD, RMSprop, Adam from keras import backend as K from keras.constraints import maxnorm import tensorflow as tf def emnist_model(): model = Sequential() model.add(Convolution2D(filters=32, kernel_size=(3, 3), padding='valid', input_shape=(28, 28, 1), activation='relu')) model.add(Convolution2D(filters=64, kernel_size=(3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(512, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(len(emnist_labels), activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adadelta', metrics=['accuracy']) return model

As you can see, this is a classic convolutional network that highlights certain features of the image (the number of filters is 32 and 64), to the “output” of which is connected the “linear” MLP network, which forms the final result.

Neural network training

Let's move on to the longest stage - training the network. To do this, we will take the EMNIST database, which can be downloaded from the link (archive size 536Mb).

To read the database, use the idx2numpy library. Prepare data for training and validation. 

 import idx2numpy emnist_path = '/home/Documents/TestApps/keras/emnist/' X_train = idx2numpy.convert_from_file(emnist_path + 'emnist-byclass-train-images-idx3-ubyte') y_train = idx2numpy.convert_from_file(emnist_path + 'emnist-byclass-train-labels-idx1-ubyte') X_test = idx2numpy.convert_from_file(emnist_path + 'emnist-byclass-test-images-idx3-ubyte') y_test = idx2numpy.convert_from_file(emnist_path + 'emnist-byclass-test-labels-idx1-ubyte') X_train = np.reshape(X_train, (X_train.shape[0], 28, 28, 1)) X_test = np.reshape(X_test, (X_test.shape[0], 28, 28, 1)) print(X_train.shape, y_train.shape, X_test.shape, y_test.shape, len(emnist_labels)) k = 10 X_train = X_train[:X_train. shape[0] // k] y_train = y_train[:y_train.shape[0] // k] X_test = X_test[:X_test.shape[0] // k] y_test = y_test[:y_test.shape[0] // k] #Normalize X_train = X_train.astype(np.float32) X_train /= 255.0 X_test = X_test.astype(np.float32) X_test /= 255.0 x_train_cat = keras.utils.to_categorical(y_train, len(emnist_labels)) y_test_cat = keras.utils.to_categorical(y_test, len(emnist_labels))

We have prepared two sets, for training and validation. The symbols themselves are ordinary arrays that are easy to display:

We also use only 1/10 of the dataset for training (parameter k), otherwise the process will take at least 10 hours.

We start the network training, at the end of the process we save the trained model to disk. 

 # Set a learning rate reduction learning_rate_reduction = keras.callbacks.ReduceLROnPlateau(monitor='val_accuracy', patience=3, verbose=1, factor=0.5, min_lr=0.00001) model.fit(X_train, x_train_cat, validation_data=(X_test, y_test_cat), callbacks=[learning_rate_reduction], batch_size=64, epochs=30) model. save('emnist_letters.h5')

The training process itself takes about half an hour:

This needs to be done only once, then we will use the already saved model file. When the training is over, everything is ready, you can recognize the text.

Identification

For recognition, we load the model and call the predict_classes function. 

 model = keras.models.load_model('emnist_letters.h5') def emnist_predict_img(model, img): img_arr = np.expand_dims(img, axis=0) img_arr = 1 - img_arr/255.0 img_arr[0] = np.rot90(img_arr[0], 3) img_arr[0] = np.fliplr(img_arr[0]) img_arr = img_arr.reshape((1, 28, 28, 1)) predict = model.predict([img_arr]) result = np.argmax(predict, axis=1) return chr(emnist_labels[result[0]])

As it turned out, the images in the dataset were initially rotated, so we have to rotate the image before recognition.

The final function, which takes an image file as input and a string as output, takes only 10 lines of code: 

 def img_to_str(model: Any, image_file: str): letters = letters_extract(image_file) s_out="" for i in range(len(letters)): dn = letters[i+1][0] - letters[i][0] - letters[i][1] if i < len(letters) - 1 else 0 s_out += emnist_predict_img(model, letters[i][2]) if (dn > letters[i][1]/4): s_out += ' ' return s_out

Here we use the previously saved character width to add spaces if the gap between letters is more than 1/4 of a character.

Usage example: 

 model = keras.models.load_model('emnist_letters.h5') s_out = img_to_str(model, "hello_world.png") print(s_out)

Result:

A funny feature - the neural network "mixed up" the letter "O" and the number "0", which, however, is not surprising because The original EMNIST set contains handwritten letters and numbers that do not quite look like printed ones. Ideally, to recognize screen texts, you need to prepare a separate set based on screen fonts, and train the neural network on it.

Conclusion

As you can see, pots are not fired by gods, and what once seemed like “magic” is done quite easily with the help of modern libraries.

Since Python is cross-platform, the code will work everywhere, on Windows, Linux and OSX. It seems that Keras is also ported to iOS/Android, so theoretically, the trained model can be used on mobile devices as well.

For those who want to experiment on their own, the source code is under the spoiler.

keras_emnist.py 

 # Code source: [email protected] import os # Force CPU # os.environ["CUDA_VISIBLE_DEVICES"] = "-1" # debug messages # 0 = all messages are logged (default behavior) # 1 = INFO messages are not printed # 2 = INFO and WARNING messages are not printed # 3 = INFO, WARNING, and ERROR messages are not printed os. environ['TF_CPP_MIN_LOG_LEVEL'] = '3' import cv2 import imghdr import numpy as np import pathlib from tensorflow import keras from keras.models import Sequential from keras import optimizers from keras.layers import Convolution2D, MaxPooling2D, Dropout, Flatten, Dense, Reshape, LSTM, BatchNormalization from keras.optimizers import SGD, RMSprop, Adam from keras import backend as K from keras.constraints import maxnorm import tensorflow as tf from scipy import io as spio import idx2numpy # sudo pip3 install idx2numpy from matplotlib import pyplot as plt from typing import * import time # dataset: # https://www.nist.gov/node/1298471/emnist-dataset # https://www.itl.nist.gov/iaui/vip/cs_links/EMNIST/gzip.zip def cnn_print_digit(d): print(d.shape) for x in range(28): s="" for y in range(28): s += "{0:.1f} ".format(d[28*y + x]) print(s) def cnn_print_digit_2d(d): print(d.shape) for y in range(d.shape[0]): s="" for x in range(d. shape[1]): s += "{0:.1f} ".format(d[x][y]) print(s) emnist_labels = [48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 97, 98, 99, 100 , 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122] def emnist_model(): model = Sequential() model.add(Convolution2D(filters=32, kernel_size=(3, 3), padding='valid', input_shape=(28, 28, 1), activation='relu')) model.add(Convolution2D(filters=64, kernel_size=(3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(512, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(len(emnist_labels), activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adadelta', metrics=['accuracy']) return model def emnist_model2(): model = Sequential() # In Keras there are two options for padding: same or valid. Same means we pad with the number on the edge and valid means no padding. model.add(Convolution2D(filters=32, kernel_size=(3, 3), activation='relu', padding='same', input_shape=(28, 28, 1))) model.add(MaxPooling2D((2, 2))) model.add(Convolution2D(64, (3, 3), activation='relu', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Convolution2D(128, (3, 3), activation='relu', padding='same')) model.add(MaxPooling2D((2, 2))) # model.add(Conv2D(128, (3, 3), activation='relu', padding='same')) #model.add(MaxPooling2D((2, 2))) ##model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(512, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(len(emnist_labels), activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adadelta', metrics=['accuracy']) return model def emnist_model3(): model = Sequential() model.add(Convolution2D(filters=32, kernel_size=(3, 3), padding='same', input_shape=(28, 28, 1), activation='relu')) model. add(Convolution2D(filters=32, kernel_size=(3, 3), padding='same', activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Convolution2D(filters=64, kernel_size=(3, 3), padding='same', activation='relu')) model.add(Convolution2D(filters=64, kernel_size=(3, 3), padding='same', activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(512, activation="relu")) model.add(Dropout(0.5)) model.add(Dense(len(emnist_labels), activation="softmax")) model.compile(loss='categorical_crossentropy', optimizer=RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0), metrics=['accuracy']) return model def emnist_train(model): t_start = time.time() emnist_path = 'D:\\Temp\\1\\' X_train = idx2numpy.convert_from_file(emnist_path + 'emnist-byclass-train-images-idx3-ubyte') y_train = idx2numpy.convert_from_file(emnist_path + 'emnist-byclass-train-labels-idx1-ubyte') X_test = idx2numpy. convert_from_file(emnist_path + 'emnist-byclass-test-images-idx3-ubyte') y_test = idx2numpy.convert_from_file(emnist_path + 'emnist-byclass-test-labels-idx1-ubyte') X_train = np.reshape(X_train, (X_train.shape[0], 28, 28, 1)) X_test = np.reshape(X_test, (X_test.shape[0], 28, 28, 1)) print(X_train.shape, y_train.shape, X_test.shape, y_test.shape, len(emnist_labels)) #Test: k = 10 X_train = X_train[:X_train.shape[0] // k] y_train = y_train[:y_train.shape[0] // k] X_test = X_test[:X_test.shape[0] // k] y_test = y_test[:y_test.shape[0] // k] #Normalize X_train = X_train.astype(np.float32) X_train /= 255.0 X_test = X_test.astype(np.float32) X_test /= 255.0 x_train_cat = keras.utils.to_categorical(y_train, len(emnist_labels)) y_test_cat = keras.utils.to_categorical(y_test, len(emnist_labels)) # Set a learning rate reduction learning_rate_reduction = keras.callbacks.ReduceLROnPlateau(monitor='val_accuracy', patience=3, verbose=1, factor=0. 5, min_lr=0.00001) model.fit(X_train, x_train_cat, validation_data=(X_test, y_test_cat), callbacks=[learning_rate_reduction], batch_size=64, epochs=30) print("Training done, dT:", time.time() - t_start) def emnist_predict(model, image_file): img = keras.preprocessing.image.load_img(image_file, target_size=(28, 28), color_mode='grayscale') emnist_predict_img(model, img) def emnist_predict_img(model, img): img_arr = np.expand_dims(img, axis=0) img_arr = 1 - img_arr/255.0 img_arr[0] = np.rot90(img_arr[0], 3) img_arr[0] = np.fliplr(img_arr[0]) img_arr = img_arr.reshape((1, 28, 28, 1)) predict = model.predict([img_arr]) result = np.argmax(predict, axis=1) return chr(emnist_labels[result[0]]) def letters_extract(image_file: str, out_size=28): img = cv2.imread(image_file) gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY) img_erode = cv2.erode(thresh, np.ones((3, 3), np.uint8), iterations=1) # Get contours contours, hierarchy = cv2. findContours(img_erode, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE) output = img.copy() letters = [] for idx, contour in enumerate(contours): (x, y, w, h) = cv2.boundingRect(contour) # print("R", idx, x, y, w, h, cv2.contourArea(contour), hierarchy[0][idx]) # hierarchy[i][0]: the index of the next contour of the same level # hierarchy[i][1]: the index of the previous contour of the same level # hierarchy[i][2]: the index of the first child # hierarchy[i][3]: the index of the parent if hierarchy[0][idx][3] == 0: cv2.rectangle(output, (x, y), (x + w, y + h), (70, 0, 0), 1) letter_crop = gray[y:y + h, x:x + w] # print(letter_crop. shape) # Resize letter canvas to square size_max = max(w, h) letter_square = 255 * np.ones(shape=[size_max, size_max], dtype=np.uint8) if w > h: # Enlarge image top-bottom # ------ # ====== # ------ y_pos = size_max//2 - h//2 letter_square[y_pos:y_pos + h, 0:w] = letter_crop elif w < h: # Enlarge image left-right # --||-- x_pos = size_max//2 - w//2 letter_square[0:h, x_pos:x_pos + w] = letter_crop else: letter_square = letter_crop # Resize letter to 28x28 and add letter and its X-coordinate letters. append((x, w, cv2.resize(letter_square, (out_size, out_size), interpolation=cv2.INTER_AREA))) # Sort array in place by X-coordinate letters.sort(key=lambda x: x[0], reverse=False) # cv2.imshow("Input", img) # # cv2.imshow("Gray", thresh) # cv2.imshow("Enlarged", img_erode) # cv2.imshow("output", output) # cv2.imshow("0", letters[0][2]) # cv2.imshow("1", letters[1][2]) # cv2.imshow("2", letters[2][2]) # cv2.imshow("3", letters[3][2]) # cv2.imshow("4", letters[4][2]) # cv2.waitKey(0) return letters def img_to_str(model: Any, image_file: str): letters = letters_extract(image_file) s_out="" for i in range(len(letters)): dn = letters[i+1][0] - letters[i][0] - letters[i][1] if i < len(letters) - 1 else 0 s_out += emnist_predict_img(model, letters[i][2]) if (dn > letters[i][1]/4): s_out += ' ' return s_out if __name__ == "__main__": # model = emnist_model() # emnist_train(model) #model. save('emnist_letters.h5') model = keras.models.load_model('emnist_letters.h5') s_out = img_to_str(model, "hello_world.png") print(s_out)

As usual, good luck with your experiments.

Visual introduction to neural networks using the example of digit recognition

With the help of many animations, a visual introduction to the learning process of a neural network is given using the example of a digit recognition task and a perceptron model.

Articles on the topic of what artificial intelligence is have been written for a long time. But the mathematical side of the coin :)

We continue the series of first-class illustrative courses 3Blue1Brown (see our previous reviews on linear algebra and math analysis) with a course on neural networks.

The first video is devoted to the structure of the components of the neural network, the second - to its training, the third - to the algorithm of this process. As a task for training, the classical task of recognizing numbers written by hand was taken.

A multilayer perceptron is considered in detail - a basic (but already quite complex) model for understanding any more modern versions of neural networks.

The purpose of the first video is to show what a neural network is. Using the example of the problem of digit recognition, the structure of the components of the neural network is visualized. The video has Russian subtitles.

Number Recognition Problem Statement

Let's say you have the number 3 drawn at an extremely low resolution of 28x28 pixels. Your brain can easily recognize this number.

From a computational standpoint, it's amazing how easy the brain is to perform this operation, even though the exact arrangement of the pixels varies greatly from one image to the next. Something in our visual cortex decides that all threes, no matter how they are depicted, represent the same entity. Therefore, the task of recognizing numbers in this context is perceived as simple.

But if you were asked to write a program that takes an image of any number as an input in the form of an array of 28x28 pixels and outputs the "entity" itself - a number from 0 to 9, then this task would cease to seem simple.

As the name suggests, the structure of the neural network is somewhat close to the structure of the neural network of the brain. For now, for simplicity, we will imagine that in the mathematical sense, in neural networks, neurons are understood as a certain container containing a number from zero to one.

Neuron activation. Neural network layers

Since our grid consists of 28x28=784 pixels, let there be 784 neurons containing different numbers from 0 to 1: the closer the pixel is to white, the closer the corresponding number is to one. These numbers filling the grid will be called activations of neurons. You can imagine this as if the neuron lights up like a light bulb when it contains a number close to 1 and goes out when the number is close to 0.

The described 784 neurons form the first layer of the neural network. The last layer contains 10 neurons, each corresponding to one of the ten digits. In these numbers, activation is also a number from zero to one, reflecting how confident the system is that the input image contains the corresponding digit.

There are also a couple of middle layers, called hidden layers, which we'll get to shortly. The choice of the number of hidden layers and the neurons they contain is arbitrary (we chose 2 layers of 16 neurons each), but usually they are chosen from certain ideas about the task being solved by the neural network.

The principle of the neural network is that the activation in one layer determines the activation in the next. Being excited, a certain group of neurons causes the excitation of another group. If we pass the trained neural network to the first layer the activation values ​​according to the brightness of each pixel of the image, the chain of activations from one layer of the neural network to the next will lead to the preferential activation of one of the neurons of the last layer corresponding to the recognized digit - the choice of the neural network.

Purpose of hidden layers

Before delving into the math of how one layer affects the next, how learning occurs, and how the neural network solves the problem of recognizing numbers, let's discuss why such a layered structure can act intelligently at all. What do intermediate layers do between input and output layers?

Figure Image Layer

In the process of digit recognition, we bring the various components together. For example, a nine consists of a circle on top and a line on the right. The figure eight also has a circle at the top, but instead of a line on the right, it has a paired circle at the bottom. The four can be represented as three lines connected in a certain way. And so on.

In the idealized case, one would expect each neuron from the second layer to correspond to one of these components. And, for example, when you feed an image with a circle at the top to the neural network, there is a certain neuron whose activation will become closer to one. Thus, the transition from the second hidden layer to the output corresponds to the knowledge of which set of components corresponds to which digit.

Layer of images of structural units

The circle recognition task can also be divided into subtasks. For example, to recognize various small faces from which it is formed. Likewise, a long vertical line can be thought of as a pattern connecting several smaller pieces. Thus, it can be hoped that each neuron from the first hidden layer of the neural network performs the operation of recognizing these small edges.

Thus entered image leads to the activation of certain neurons of the first hidden layer, defining characteristic small pieces, these neurons in turn activate larger shapes, as a result activating the neuron of the output layer associated with a certain number.

Whether or not the neural network will act this way is another matter that you will return to when discussing the network learning process. However, this can serve as a guide for us, a kind of goal of such a layered structure.

On the other hand, such a definition of edges and patterns is useful not only in the problem of digit recognition, but also in the problem of pattern detection in general.

And not only for recognition of numbers and images, but also for other intellectual tasks that can be divided into layers of abstraction. For example, for speech recognition, individual sounds, syllables, words, then phrases, more abstract thoughts, etc. are extracted from raw audio.

Determining the recognition area

To be specific, let's now imagine that the goal of a single neuron in the first hidden layer is to determine if the picture contains a face in the area marked in the figure.

The first question is: what settings should the neural network have in order to be able to detect this pattern or any other pixel pattern.

Assign a numerical weight w i to each connection between our neuron and the neuron from the input layer. Then we take all the activations from the first layer and calculate their weighted sum according to these weights.

Since the number of weights is the same as the number of activations, they can also be mapped to a similar grid. We will denote positive weights with green pixels, and negative weights with red pixels. The brightness of the pixel will correspond to the absolute value of the weight.

Now, if we set all weights to zero, except for the pixels that match our pattern, then the weighted sum is the sum of the activation values ​​of the pixels in the region of interest.

If you want to determine if there is an edge, you can add red weight faces around the green weight rectangle, corresponding to negative weights. Then the weighted sum for this area will be maximum when the average pixels of the image in this area are brighter, and the surrounding pixels are darker.

Activation scaling to the interval [0, 1]

By calculating such a weighted sum, you can get any number in a wide range of values. In order for it to fall within the required range of activations from 0 to 1, it is reasonable to use a function that would “compress” the entire range to the interval [0, 1].

The sigmoid logistic function is often used for this scaling. The greater the absolute value of the negative input number, the closer the sigmoid output value is to zero. The larger the value of the positive input number, the closer the value of the function is to one.

Thus, neuron activation is essentially a measure of how positive the corresponding weighted sum is. To prevent the neuron from firing at small positive numbers, you can add a negative number to the weighted sum - a bias, which determines how large the weighted sum should be in order to activate the neuron.

So far we have only talked about one neuron. Each neuron from the first hidden layer is connected to all 784 pixel neurons of the first layer. And each of these 784 compounds will have a weight associated with it. Also, each of the neurons in the first hidden layer has a shift associated with it, which is added to the weighted sum before this value is "compressed" by the sigmoid. Thus, for the first hidden layer, there are 784x16 weights and 16 shifts.

Connections between other layers also contain the weights and offsets associated with them. Thus, for the given example, about 13 thousand weights and shifts that determine the behavior of the neural network act as adjustable parameters.

To train a neural network to recognize numbers means to force the computer to find the correct values ​​for all these numbers in such a way that it solves the problem. Imagine adjusting all those weights and manually shifting. This is one of the most effective arguments to interpret the neural network as a black box - it is almost impossible to mentally track the joint behavior of all parameters.

Description of a neural network in terms of linear algebra

Let's discuss a compact way of mathematical representation of neural network connections. Combine all activations of the first layer into a column vector. We combine all the weights into a matrix, each row of which describes the connections between the neurons of one layer with a specific neuron of the next (in case of difficulty, see the linear algebra course we described). As a result of multiplying the matrix by the vector, we obtain a vector corresponding to the weighted sums of activations of the first layer. We add the matrix product with the shift vector and wrap the sigmoid function to scale the ranges of values. As a result, we get a column of corresponding activations.

Obviously, instead of columns and matrices, as is customary in linear algebra, one can use their short notation. This makes the corresponding code both simpler and faster, since the machine learning libraries are optimized for vector computing.

Neuronal activation clarification

It's time to refine the simplification we started with. Neurons correspond not just to numbers - activations, but to activation functions that take values ​​from all neurons of the previous layer and calculate output values ​​in the range from 0 to 1.

In fact, the entire neural network is one large learning-adjustable function with 13,000 parameters that takes 784 input values ​​and gives the probability that the image corresponds to one of the ten digits intended for recognition. However, despite its complexity, this is just a function, and in a sense it is logical that it looks complicated, because if it were simpler, this function would not be able to solve the problem of recognizing digits.

As a supplement, let's discuss which activation functions are currently used to program neural networks.

Addition: a little about the activation functions. Comparison of the sigmoid and ReLU

Let us briefly touch on the topic of functions used to "compress" the interval of activation values. The sigmoid function is an example that emulates biological neurons and was used in early work on neural networks, but the simpler ReLU function is now more commonly used to facilitate neural network training.

The ReLU function corresponds to the biological analogy that neurons may or may not be active. If a certain threshold is passed, then the function is triggered, and if it is not passed, then the neuron simply remains inactive, with an activation equal to zero.

It turned out that for deep multilayer networks, the ReLU function works very well and it often makes no sense to use the more complex sigmoid function to calculate.

The question arises: how does the network described in the first lesson find the appropriate weights and shifts only from the received data? This is what the second lesson is about.

In general, the algorithm is to show the neural network a set of training data representing pairs of images of handwritten numbers and their abstract mathematical representations.

In general terms

As a result of training, the neural network must correctly distinguish numbers from previously unrepresented test data. Accordingly, the ratio of the number of acts of correct recognition of digits to the number of elements of the test sample can be used as a test for training the neural network.

Where does training data come from? The problem under consideration is very common, and to solve it, a large MNIST database was created, consisting of 60 thousand labeled data and 10 thousand test images.

Cost function

Conceptually, the task of training a neural network is reduced to finding the minimum of a certain function - the cost function. Let's describe what it is.

As you remember, each neuron of the next layer is connected to the neuron of the previous layer, while the weights of these connections and the total shift determine its activation function. In order to start somewhere, we can initialize all these weights and shifts with random numbers.

Accordingly, at the initial moment, an untrained neural network in response to an image of a given number, for example, an image of a triple, the output layer gives a completely random answer.

To train the neural network, we will introduce a cost function, which will, as it were, tell the computer in the event of a similar result: “No, bad computer! The activation value must be zero for all neurons except for the one that is correct.”

Setting the cost function for digit recognition

Mathematically, this function represents the sum of the squared differences between the actual activation values ​​of the output layer and their ideal values. For example, in the case of a triple, the activation must be zero for all neurons, except for the one corresponding to the triple, for which it is equal to one.

It turns out that for one image we can determine one current value of the cost function. If the neural network is trained, this value will be small, ideally tending to zero, and vice versa: the larger the value of the cost function, the worse the neural network is trained.

Thus, in order to subsequently determine how well the neural network was trained, it is necessary to determine the average value of the cost function for all images of the training set.

This is a rather difficult task. If our neural network has 784 pixels at the input, 10 values ​​at the output and requires 13 thousand parameters to calculate them, then the cost function is a function of these 13 thousand parameters, it produces one single cost value that we want to minimize, and at the same time in the entire training set serves as parameters.

How to change all these weights and shifts so that the neural network is trained?

Gradient Descent

To start, instead of representing a function with 13k inputs, let's start with a function of one variable, C(w). As you probably remember from the course of mathematical analysis, in order to find the minimum of a function, you need to take the derivative.

However, the shape of a function can be very complex, and one flexible strategy is to start at some arbitrary point and step down the value of the function. By repeating this procedure at each subsequent point, one can gradually come to a local minimum of the function, as does a ball rolling down a hill.

As shown in the figure, a function can have many local minima, and which local minimum the algorithm ends up in depends on the choice of starting point, and there is no guarantee that the minimum found is the minimum possible value of the cost function. This must be kept in mind. In addition, in order not to "slip" the value of the local minimum, you need to change the step size in proportion to the slope of the function.

Slightly complicating this task, instead of a function of one variable, you can represent a function of two variables with one output value. The corresponding function for finding the direction of the fastest descent is the negative gradient -∇C. The gradient is calculated, a step is taken in the direction of -∇С, the procedure is repeated until we are at the minimum.

The described idea is called gradient descent and can be applied to find the minimum of not only a function of two variables, but also 13 thousand, and any other number of variables. Imagine that all weights and shifts form one large column vector w. For this vector, you can calculate the same cost function gradient vector and move in the appropriate direction by adding the resulting vector to the w vector. And so repeat this procedure until the function С(w) comes to a minimum.

Gradient Descent Components

For our neural network, steps towards a lower cost function value will mean less random behavior of the neural network in response to training data. The algorithm for efficiently calculating this gradient is called backpropagation and will be discussed in detail in the next section.

For gradient descent, it is important that the output values ​​of the cost function change smoothly. That is why activation values ​​are not just binary values ​​of 0 and 1, but represent real numbers and are in the interval between these values.

Each gradient component tells us two things. The sign of a component indicates the direction of change, and the absolute value indicates the effect of this component on the final result: some weights contribute more to the cost function than others.

Checking the assumption about the assignment of hidden layers

Let's discuss the question of how the layers of the neural network correspond to our expectations from the first lesson. If we visualize the weights of the neurons of the first hidden layer of the trained neural network, we will not see the expected figures that would correspond to the small constituent elements of the numbers. We will see much less clear patterns corresponding to how the neural network has minimized the cost function.

On the other hand, the question arises, what to expect if we pass an image of white noise to the neural network? It could be assumed that the neural network should not produce any specific number and the neurons of the output layer should not be activated or, if they are activated, then in a uniform way. Instead, the neural network will respond to a random image with a well-defined number.

Although the neural network performs digit recognition operations, it has no idea how they are written. In fact, such neural networks are a rather old technology developed in the 80s-90 years. However, it is very useful to understand how this type of neural network works before understanding modern options that can solve various interesting problems. But the more you dig into what the hidden layers of a neural network are doing, the less intelligent the neural network seems to be.

Learning on structured and random data

Consider an example of a modern neural network for recognizing various objects in the real world.

What happens if you shuffle the database so that the object names and images no longer match? Obviously, since the data is labeled randomly, the recognition accuracy on the test set will be useless. However, at the same time, on the training sample, you will receive recognition accuracy at the same level as if the data were labeled in the right way.

Millions of weights on this particular modern neural network will be fine-tuned to exactly match the data and its markers. Does the minimization of the cost function correspond to some image patterns, and does learning on randomly labeled data differ from training on incorrectly labeled data?

If you train a neural network for the recognition process on randomly labeled data, then training is very slow, the cost curve from the number of steps taken behaves almost linearly. If training takes place on structured data, the value of the cost function decreases in a much smaller number of iterations.

Backpropagation is a key neural network training algorithm. Let us first discuss in general terms what the method consists of.

Neuron activation control

Each step of the algorithm uses in theory all examples of the training set. Let us have an image of a 2 and we are at the very beginning of training: weights and shifts are set randomly, and some random pattern of output layer activations corresponds to the image.

We cannot directly change the activations of the final layer, but we can influence the weights and shifts to change the activation pattern of the output layer: decrease the activation values ​​of all neurons except the corresponding 2, and increase the activation value of the required neuron. In this case, the increase and decrease is required the stronger, the farther the current value is from the desired one.

Neural network configuration options

Let's focus on one neuron, corresponding to the activation of neuron 2 on the output layer. As we remember, its value is the weighted sum of the activations of the neurons of the previous layer plus the shift, wrapped in a scaling function (sigmoid or ReLU).

So to increase the value of this activation, we can:

  1. Increase the shift b.
  2. Increase weights w i .
  3. Swap previous layer activations a i .

From the weighted sum formula, it can be seen that the weights corresponding to connections with the most activated neurons make the greatest contribution to neuron activation. A strategy similar to biological neural networks is to increase the weights w i in proportion to the activation value a i of the corresponding neurons of the previous layer. It turns out that the most activated neurons are connected to the neuron that we only want to activate with the most "strong" connections.

Another close approach is to change the activations of neurons of the previous layer a i in proportion to the weights w i . We cannot change the activation of neurons, but we can change the corresponding weights and shifts and thus affect the activation of neurons.

Backpropagation

The penultimate layer of neurons can be considered similarly to the output layer. You collect information about how the activations of neurons in this layer would have to change in order for the activations of the output layer to change.

It is important to understand that all these actions occur not only with the neuron corresponding to the two, but also with all the neurons of the output layer, since each neuron of the current layer is connected to all the neurons of the previous one.

Having summed up all these necessary changes for the penultimate layer, you understand how the second layer from the end should change. Then, recursively, you repeat the same process to determine the weight and shift properties of all layers.

Classic Gradient Descent

As a result, the entire operation on one image leads to finding the necessary changes of 13 thousand weights and shifts. By repeating the operation on all examples of the training sample, you get the change values ​​for each example, which you can then average for each parameter separately.

The result of this averaging is the negative gradient column vector of the cost function.

Stochastic Gradient Descent

Considering the entire training set to calculate a single step slows down the gradient descent process. So the following is usually done.

The data of the training sample are randomly mixed and divided into subgroups, for example, 100 labeled images. Next, the algorithm calculates the gradient descent step for one subgroup.

This is not exactly a true gradient for the cost function, which requires all the training data, but since the data is randomly selected, it gives a good approximation, and, importantly, allows you to significantly increase the speed of calculations.

If you build the learning curve of such a modernized gradient descent, it will not look like a steady, purposeful descent from a hill, but like a winding trajectory of a drunk, but taking faster steps and also coming to a function minimum.

This approach is called stochastic gradient descent.

Supplement. Back propagation math

Now let's look a little more formally at the mathematical background of the backpropagation algorithm.

Primitive neural network model

Let's start with an extremely simple neural network consisting of four layers, where each layer has only one neuron. Accordingly, the network has three weights and three shifts. Consider how sensitive the function is to these variables.

Let's start with the connection between the last two neurons. We denote the last layer L, the penultimate layer L-1, and the activations of the considered neurons lying in them a (L) , a (L-1) .

Cost function

Imagine that the desired activation value of the last neuron given to the training examples is y, equal to, for example, 0 or 1. Thus, the cost function is defined for this example as

C 0 = (a ( L) - y) 2 .

Recall that the activation of this last neuron is given by the weighted sum, or rather the scaling function of the weighted sum: (L)).

For brevity, the weighted sum can be denoted by a letter with the appropriate index, for example z (L) :

a (L) = σ (z (L) ).

Consider how small changes in weight w affect the value of the cost function (L) . Or in mathematical terms, what is the derivative of the cost function with respect to weight ∂C 0 /∂w (L) ?

It can be seen that the change in C 0 depends on the change in a (L) , which in turn depends on the change in z (L) , which depends on w (L) . According to the rule of taking similar derivatives, the desired value is determined by the product of the following partial derivatives:

∂C 0 /∂w (L) = ∂z (L) /∂w (L) • ∂a (L) /∂z (L) • ∂C 0 /∂a (L) .

Definition of derivatives

Calculate the corresponding derivatives: and desired.

The average derivative in the chain is simply the derivative of the scaling function:

∂a (L) /∂z (L) = σ'(z (L) )

/∂w (L) = a (L-1)

Thus, the corresponding change is determined by how activated the previous neuron is. This is consistent with the idea mentioned above that a stronger connection is formed between neurons that light up together.

Final expression:

∂C 0 /∂w (L) = 2(a (L) - y) σ'(z (L) ) a (L-1)

Recall that a certain derivative is only for the cost of a single example of the training sample C 0 . For the cost function C, as we remember, it is necessary to average over all examples of the training sample: The resulting average value for a specific w (L) is one of the components of the cost function gradient. The consideration for shifts is identical to the above consideration for weights.

Having obtained the corresponding derivatives, we can continue the consideration for the previous layers.

Model with many neurons in the layer

However, how to make the transition from layers containing one neuron to the initially considered neural network.

Learn more