Home » Misc » Teaching number sense

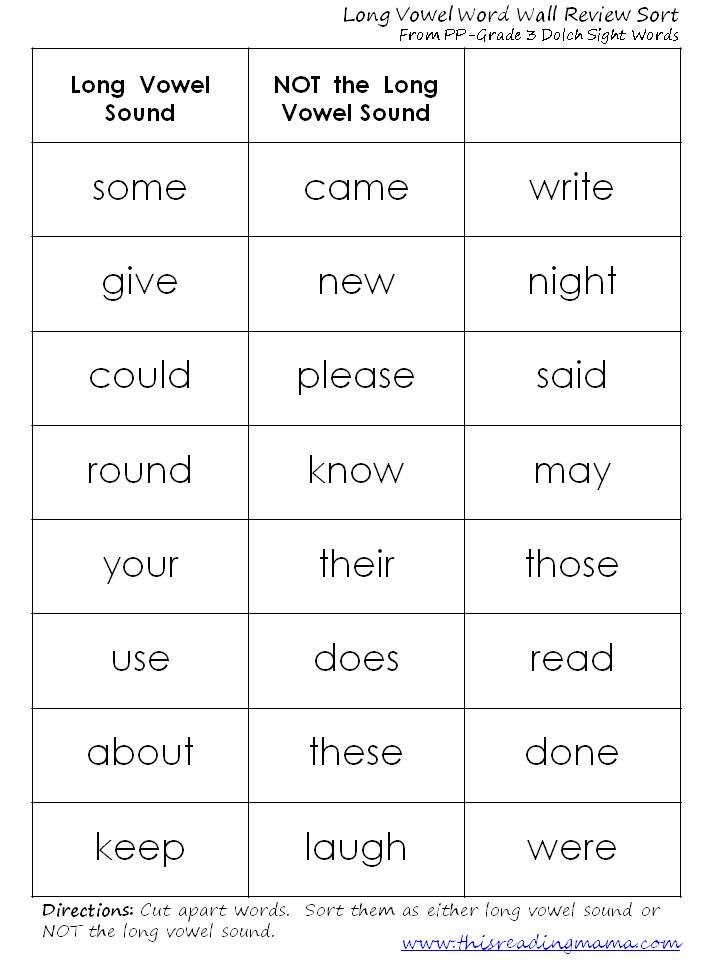
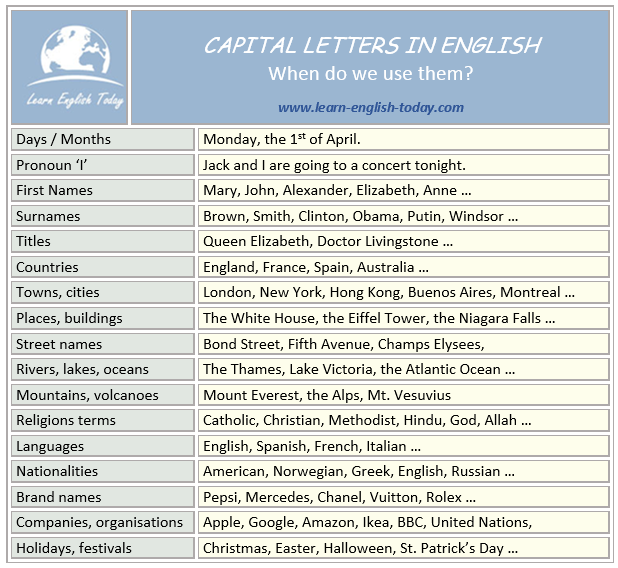
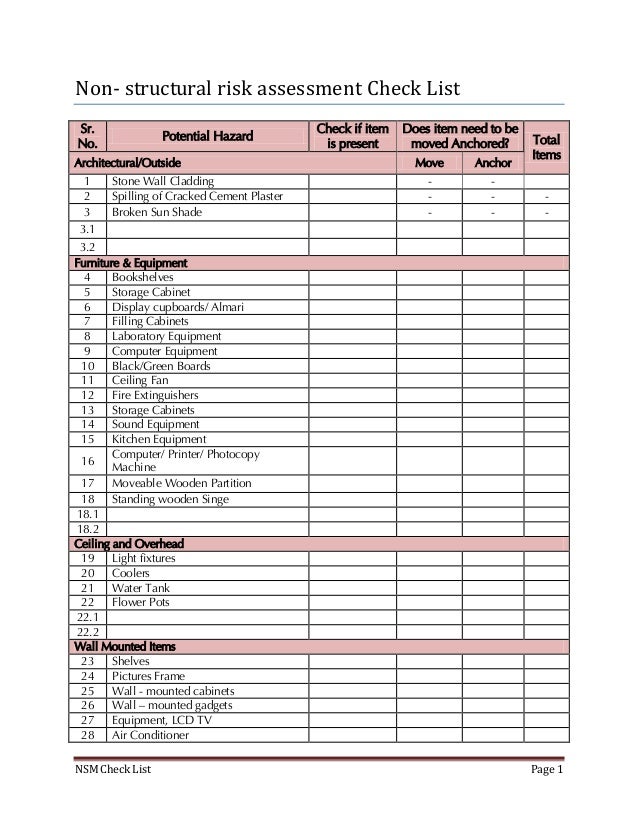
Teaching number sense


8 Strategies to Teach Number Sense to Pre-K and Elementary School Kids

Even as toddlers, the littlest of learners are learning to use their mathematical minds. The word “more” is one of the first words kids learn at the dinner table, and they are quick to learn that they want the most candy or the biggest slice of pie at dessert. Kids are constantly evaluating their world and comparing objects by quantity, size, shape, and more! 

Since kids have this natural capacity to make sense of their world through mathematical concepts, it’s important to take those primitive skills to the next level by helping them make connections between their everyday observations and a more solid understanding of numbers. That’s why it’s so important to support your child’s development of number sense. But how can a parent begin teaching number sense to ensure such a concrete understanding of math concepts? 

If you’re wondering how to teach number sense to your child, try the following strategies to support your little learner’s early math skills: 

Storytime-advertising-container

Adsense-container

Noticing Everyday Math

Nothing is more important than engaging with your child and talking about the math you and your child experience daily. Talk about prices, budget, and quantity at the grocery store, and show your child how you use math to manage money. Practice fractions while cooking and baking, and take note of the shapes found in road signs and outdoors. Talking about the math found in everyday life sets a purpose for using and performing math processes. If kids know why math is so important in real life, they will be excited to find reasons to use it!  

It’s All About the Process

Oftentimes, we get caught up with finding an answer to a math problem that we pay little attention to the process we take to solve it. Sometimes we impatiently want to find the answer quickly and move on to the next task. Instead, teach your child that the most important part of solving a problem is the way they solve it. To do this, encourage your child to look check their work and find mistakes they might have made.    

Strategies for Preschool and Kindergarten Kids

Verbalizing Math Concepts

When a child describes their work and explains the process they took to solve a problem or make an observation, they are more likely to internalize what they’ve learned. This simply means kids will remember more when they talk about it. When working with your child on a homework assignment, encourage your child to tell you how they plan to solve the problem. During completion, have your child tell you about it each step of the way. In doing so, your child will develop number sense as they internalize and understand the process they took to solve the problem. 

Dot Cards

Subtilizing is the skill that refers to instantly and visually recognizing a group of objects and knowing the number just by looking. This is an important mental math skill that aids in solving problems, as well as understanding numbers. Using dot cards can help your child build this critical skill by gaining more practice recognizing groups of dots on the card. 

Using Manipulatives

Learning numbers for kids can be a tough task. To make numbers make sense on paper, it’s helpful to use manipulatives that kids can use to make sense of quantity. A quick Google search for “math manipulatives” will lead you to online vendors who sell place value blocks, counters, magnet manipulatives, and more.  Manipulatives give your child a concrete way to represent numbers. In a pinch, you can even visually show your child simple addition and subtraction using Skittles or M&M’s to demonstrate the concepts for deeper understanding of math.

Check out our collection of fun math videos to satiate your kid's thirst for early number sense concepts. 

Strategies for Elementary School Kids

Number Lines

There’s more than one way to solve math problems, and kids should learn different strategies to increase their number sense. For instance, using a number line can help kids make the connection between addition and subtraction or practice place value. Kids can even learn subtraction by using addition by flipping the problem around. Teaching kids multiple ways to solve problems strengthens number sense by understanding the processes they take to solve problems.   

Mental Math

When kids skip count by 2’s, 5’s, or 10’s, kids are using mental math to add. We can continue this process by asking kids to add less or more, and teaching strategies like splitting and jumping. These strategies focus on different ways to break down math problems to make difficult problems easy to solve mentally. Teaching these strategies give your child one more tool to help them understand numbers inside and out. 

Make Estimations and Predictions

Place a favorite candy in a small container, and ask your child to estimate how many candies are in the bowl. Kids can solidify their number sense by making estimations and predictions based on observations. Moreover, your child will make the connection between quantity and numbers, sharpening their number sense.

Like many adults, for some kids, math can be a source of frustration and anxiety. But solving tricky math problems doesn’t need to be so difficult if only a child understands numbers and math processes. That’s why strengthening your child’s number sense makes a world of difference. When your child has a solid understanding of numbers and how they work, your little learner will have a foundation for future math success!

 

Teaching Number Sense

What is number sense? How does it develop? How can we teach number sense to students who start school without it? Recent research in the learning sciences has found answers to each of these questions. Coming from fields of inquiry that are distinct from education, these answers provide new perspectives on what number sense is and how to teach it.

What Is Number Sense?

Research on teachers' ideas about math (Griffin & Case, 1997) reveals that many teachers define the discipline as a fixed body of knowledge involving numbers and their manipulation through rules and algorithms (Jackson, 1986). Because of their own learning experiences, many teachers believe that math is about numbers. By treating numbers as disembodied entities, these teachers focus their instruction on ensuring that their students know various math rules and the applications of those rules.

Although numbers and algorithms are clearly involved in the business of doing math, they are not the whole story—not by a long shot. Instead, mathematicians and enlightened educators see math as a set of conceptual relationships between quantities and numerical symbols. This view underpins the Principles and Standards for School Mathematics developed by the National Council of Teachers of Mathematics (2000). When teachers see math as about quantity, not numbers, they ask different questions in their classrooms: What are numbers? instead of What are the rules for manipulating numbers? Students do not simply learn and apply rules and try to find the right answer; instead, they construct and discover relationships between quantities and numbers and then examine alternative ways to describe and record these relationships.

What are the consequences of these two views for student learning? On extensive tests of number knowledge and number sense (Griffin & Case, 1997), kindergarten students who have learned to link numbers to quantities have no trouble answering the question, Which is bigger, 7 or 9? Students without this knowledge often look startled by the question, as if it isn't a meaningful thing to ask, and respond by saying “I don't know” or by making a wild guess. At the end of 1st grade, students who understand the connection between numbers and quantities have no trouble crossing out the three incorrect formulas in the following set of choices: 9 + 2 = 92; 9 + 2 = 11; 9 + 2 = 10; 9 + 2 = 7. Although some of these students make a mistake in counting and select 10 as the correct answer, they rarely, if ever, select 92 or 7 as the correct answer. In contrast, students who only learn the rules reveal a lack of understanding of the meaning of numbers and of the operation signs. Students who choose 92 as the correct answer, for example, are clearly putting numbers together, but they are not making sense of the symbolic expression that asks them to add the quantities that these symbols refer to rather than the symbols themselves.

The discipline of mathematics comprises three worlds: the actual quantities that exist in space and time; the counting numbers in the spoken language; and formal symbols, such as written numerals and operation signs. Number sense requires the construction of a rich set of relationships among these worlds. Students must first link the real quantities with the counting numbers. Only then can students connect this integrated knowledge to the world of formal symbols and gain an understanding of their meaning. To attain number sense, students need opportunities to discover and to construct relationships among these three worlds at higher and higher levels of complexity.

How Does Number Sense Develop?

Pioneering work in cognitive neuro-psychology and infant cognition tells us that human infants are born with brain structures that are specifically attuned to numerical quantities. These structures have a long evolutionary history and are at least partially independent of the brain structures that support verbal processing (Dehaene, 1997; Dehaene & Cohen, 1995; Kunzig, 1997).

These structures permit infants, for example, to distinguish a set of two objects from a set of three objects in the first few days of life (Antell & Keating, 1983) and to match a set of three sounds to a set of three objects at six months (Starkey, Spelke, & Gelman, 1990). As early as five months old, infants can even anticipate the results of transformations in small sets. For example, they register surprise if two puppets are placed behind a screen in sequence and only one is present when the screen is raised, and, conversely, show the same response if one puppet is withdrawn from two that have been placed behind a screen and two puppets are present when the screen is raised (Wynn, 1992). Whether one accepts the strong interpretation of these findings (that infants have an innate ability to represent number and to perform simple arithmetic) or prefers a weaker interpretation (that infants have a remarkable attunement to the magnitude of small sets), it is clear that a strong foundation for number sense is present in the earliest months of life.

As infants become toddlers, their natural quantitative competencies expand and they acquire language and, with it, the ability to count. By the age of 4, as documented in extensive cognitive developmental research (summarized in Griffin & Case, 1997), children have constructed two schemas: one for making global quantity comparisons and another for counting. At age 5 or 6, children experience a revolution in thought as they merge these two schemas into a single, superordinate conceptual structure for number. This new concept closely connects number with quantity and enables children to use the counting numbers without needing the presence of physical objects to make a variety of quantity judgments, such as determining how many objects they would have altogether if they had 4 of something and received 3 more.

With this new conceptual structure, which researchers believe provides the basis for all higher-level mathematics learning, children have acquired the conceptual foundation for number sense.

Students' conceptual structures continue to develop across the middle childhood years in the manner predicted by Case's (1992) cognitive developmental theory. By the age of 7 or 8, children's central conceptual structure has become more complex, permitting children to make sense of two distinct quantitative dimensions, such as 10s and 1s in math, hours and minutes in time, and dollars and cents in money. With this more complex structure, students are able to understand place value, solve double-digit arithmetic problems (12 + 54) in their heads, and tell which of two double-digit numbers (69 or 71) is bigger or smaller. Finally, by the age of 9 or 10, students' more elaborate and integrated central conceptual structure permits them to handle three quantitative variables in a coordinated fashion. With this new structure—the culmination of development in this stage—students acquire a well-developed understanding of the whole number system and are able, for example, to perform mental computations with double-digit numbers that involve borrowing and carrying (such as 13 + 39) and to solve arithmetic problems involving triple-digit numbers.

An understanding of this developmental progression is important for teaching number sense to all students. Because the progression describes the cognitive capabilities that teachers normally expect from the average child in developed societies, it exerts a profound and perhaps hidden influence on many issues of schooling, such as the age at which students start their formal math instruction and the age and grade level at which teachers introduce particular math concepts. Students who do not conform to this typical pattern may be seriously handicapped in their attempts to make sense of math instruction in school.

Because higher-level conceptual structures depend on the core concepts that students typically acquire at the age of 5 or 6, students whose core structure is not in place at the expected age will experience serious delays and will have difficulty catching up with their peers. Although most children acquire these developmental milestones at the expected age, a substantial number of students in the United States—typically those living in low-income communities—start school at the age of 5 or 6 without the central conceptual structure in place. On developmental tests of number knowledge, their performance is often nearly two years below the level of their middle-income peers (Griffin, Case, & Siegler, 1994).

We Can Teach Number Sense

  • Significant gains in number knowledge, enabling them to start 1st grade on a level commensurate with that of their middle-income peers;

  • Significant gains on a variety of transfer tests in such skill areas as time knowledge, money knowledge, and scientific reasoning, demonstrating that they could transfer their knowledge to a broad range of quantitative tasks; and

  • Average to above-average performance on a variety of measures in a follow-up study of 1st grade learning and achievement as shown in written arithmetic tests and teachers' ratings of number sense (Griffin, Case, & Siegler, 1994).

In contrast, the control groups of at-risk students whom we followed in these studies, who participated in a variety of other math programs, continued to underperform on all measures. Although they made some progress in kindergarten and 1st grade, the developmental lag that had been present at the beginning of kindergarten was still evident on measures of math learning and achievement administered at the end of 1st grade.

The Number Worlds program's success not only provides support for the psychological theory on which it was based but also suggests that teaching number sense is possible and that certain instructional principles drawn from recent theory and research on how people learn (Bransford, Brown, & Cocking, 1999; Griffin, in press) provide a powerful set of tools to teach it.

How to Teach Number Sense

Three instructional principles lie at the heart of teaching number sense and the Number Worlds program: providing rich activities for making connections, exploring and discussing concepts, and ensuring an appropriate sequence of concepts.

Rich Activities for Making Connections

The Number Worlds program provides a rich set of activities that expose students to the three worlds of math—quantities, counting, and formal symbols—and to multiple opportunities for constructing relationships among the three worlds. Games expose young students to five different forms of number representation that are common in our culture: groups of objects in Object Land, dot-set patterns and numerals in Picture Land, position on a path or line in Line Land, position on a vertical scale in Sky Land, and position on a dial in Circle Land. Motivated by the desire to win the games, students encounter many opportunities to use numbers to make sense of quantity representations. Expanded programs for four grade levels (preK-2) enable students to forge connections among these worlds at increasing levels of complexity.

The games and props in Line Land, for example, enable students to move their own bodies on a life-size, numbered teddy bear path at the preK level; to move a pawn representing the self along a game-board path, numbered 1–10, at the kindergarten level; to move a magic shoe pawn, which can leap over 10 houses in a single bound, along a game board depicting a row of 100 numbered houses at the 1st grade level; and to move a deliveryman pawn up floors and along corridors on a hotel game board with 100 numbered rooms stacked in floors of 10 units each at the 2nd grade level. Because the number system is fixed in these spatial environments and displayed in a prominent fashion, students playing the games can discover important properties of this system.

The games' rules require students to count out loud as they move through these spatial environments, ostensibly so that other players can be sure that they don't cheat. In the process of counting, predicting, and explaining their movements, students become proficient at using the standard linguistic terms—such as the language of distance—for describing quantities in this context. Most of the 1st and 2nd grade games also require students to create a written record of their actions, using the formal symbol system to record their movements and transactions to help determine the winner or who landed on a secret number. Other games and activities serve the same purpose and also expose students to other ways of representing number 5, such as in a dot-set pattern or a position on a scale.

The program provides opportunities for students to actively explore the concepts and to discuss them in a social context. The game formats require small groups of four to five students to work collaboratively to achieve the game goal. Each child actively participates by taking his or her turn, moving through the environments as the games dictate, and describing his or her movements orally or in writing. Students participate enthusiastically because the games are fun and they want to win. The games' rules, the dialogue prompts provided in the teacher's guide, the question cards included with the game props, and the wrap-up period at the end of each lesson all foster mathematical communication.

Appropriate Sequence of Concepts

The program provides a carefully graded sequence of activities that enable students to use their current understandings to construct new understandings at the next level up. Activities in the preK program enable 4-year-old students to use their conceptual structures to acquire the foundational knowledge that they will need later. Activities in the kindergarten program allow students to construct and consolidate their central conceptual structure. Within each grade level, activities have also been classified at three levels of developmental complexity. A seamless sequence of activities permits individual students to start at an appropriate individual level and to move through the normal developmental progression at a suitable pace.

What the Learning Sciences Teach

The cognitive sciences have helped us understand that in the course of development, quantity and number become solidly interconnected in children's thought around the age of 5, providing a foundation for number sense and for successful learning of arithmetic. Students who are at risk for school failure often have not achieved this developmental milestone when they start 1st grade, making it difficult for them to make sense of the math taught in school.

Fortunately, the cognitive sciences have also shown us that we can teach number sense to students who arrive at school without it by using an instructional program that is solidly grounded in recent research on how students learn and think.

Lesson 5. Principles of learning to count. Counting up to 10, up to 20 and up to 100. Counting in a column

As soon as children reach the age of 2-3 years, it is time to deal with counting with them more seriously than just telling them what “little” and “a lot” are and how much will be "2 + 2". This age period is characterized by maximum cognitive activity, and cognitive abilities reach their peak. That is why the children themselves are distinguished by curiosity and the desire to learn something that they did not know how to do before. As a result, the incoming information falls on fertile ground, and then begins to be actively used by children in their interaction with surrounding objects and people.

But when teaching a child to count, one should always keep in mind that some data can be somewhat problematic to assimilate. The child may, for example, miss some numbers from the number series or completely change their order. The reason for this is the selectivity of children's memory - for the most part, it lingers in what caused an emotional response in the mind, in particular, interest. Therefore, training should be built with a foundation on several fundamental principles that you definitely need to get acquainted with.

Content:

  • Principles for teaching children to count
  • Teaching a child to count to 10
  • Learning to count up to 20
  • Learning to count to 100
  • Learning to count with a bar
  • 3 golden rules for teaching children

1

Principles of teaching children to count

It should be noted that some of the information presented may already be familiar to you from the section on teaching children to read and the first lessons on teaching counting. But taking into account its importance and the need for application, we allow ourselves to repeat ourselves in some way.

To begin with, we note that depending on age, children can perceive information in different ways:

  • Up to 2 years. It's too early to talk about mastering the basics of counting. You just need to prepare the baby for future activities, playing with counting sticks, telling counting rhymes, fingering, etc.
  • 2 years. The child is already quite capable of perceiving ordinal counting. You can teach him to count objects one by one from 1 to 10, counting everything that comes into view.
  • 3-4 years. The child begins to count, realizing the meaning of the process. It is useful to introduce him to the simplest mathematical calculations, the grouping of objects.
  • 4-5 years. The child develops the skill of counting in the mind and develops the ability to understand abstract concepts.

Based on this, teaching children to count should be based on age characteristics.

The following principles will help you ease your little one's bumpy journey of learning to count:

  • The basis for the development of new knowledge by a child is the correspondence of information to age, the systematic nature of classes and their fascination, as well as consistency.
  • Before learning to count, it is necessary to explain to the child the meaning of the concepts "less" and "more". To do this, it is useful to draw his attention to the surrounding objects, images in books, etc.
  • When playing counting games with your child, use the concept of “equal” more often. You can ask to share blocks among family members, candies between other children in the yard, etc.
  • The child must clearly understand what it means to add and what it means to subtract. The meaning of these concepts is easy to teach using counting sticks, toys, fruits, vegetables, sweets, etc. It is important to convey to the baby that when adding, the amount increases, and when subtracting, it decreases.
  • Be sure to explain to the child that the amount does not change from changing the places of the terms.
  • First of all, teach your baby to count to ten. Before moving on to more complex numbers, you need to introduce the baby to different options for addition and subtraction within the first ten. Only after that you can move on to second-order numbers.
  • Use a ruler to teach. Counting to ten, rearrange the baby's fingers in centimeters. Although simple, this technique will set the foundation for mental arithmetic in the future.
  • Try to give the lessons a playful form. Memorization and memorization are ineffective here; they can form a negative attitude towards learning in a small student.
  • Do not teach your child to add and subtract on the abacus and do not abuse the manipulation of objects when counting. In the future, it may be difficult to teach a child to conduct mental operations without the use of visual materials.

These principles should be your foundation. Their non-observance, of course, is not catastrophic, but if you want to prevent the occurrence of unwanted problems and difficulties, as well as to avoid the most common mistakes, we advise you not to neglect them.

Now let's move on to the main part of our lesson - exercises for teaching children to count. They are divided into three categories: counting up to 10, counting up to 20 and counting up to 30.

2

0027

Teaching your child to count to 10 is the easiest way. To do this, you just need to play a few games with him at home and have a good time:

  • First, teach your baby the basics of finger counting, introducing him to the numbers from "1" to "5". But keep in mind that accustoming to counting on the fingers is much easier than weaning from it. Due to the inattention of parents, even many fifth graders often continue to count using their fingers. And this, in turn, has a negative impact on further development.
  • Find or draw your own pictures of one to five objects. But do not show the numbers themselves to the child yet, because. he can get confused. Remember that using pictures is most effective up to three years.
  • Arrange joint viewing of educational TV shows and cartoons. However, if desired, training materials can be found on the Internet.
  • Use the abacus to teach from time to time. In stores for children's goods today you can find many variations of them in very different designs (do not forget that you do not need to teach them to count).
  • Read rhymes and rhymes to your child, where counting is used, numbers and other elements of mathematics appear.
  • In your free time, count everything that surrounds you at home, on the street, in a store, etc.
  • After studying the first five digits, proceed to the study of the next five.
    • Learning to count up to 20 easy enough - using this method:

    • First you need to explain to your child that the numbers after the first nine have two digits. Explain that the first digits in these numbers are tens, and the second - units.
    • Prepare two small boxes or some other containers, as well as a couple of dozen items, preferably the same. Place 12, 13, or 14 items in the first box, and 1, 2, or 3 items in the second box. This is necessary so that the child can clearly see the difference.
    • The next step is to tell the kid that the numbers always go in the same sequence, i.e. after "10" comes "11", then "12", then "13", etc.
    • When you see that the young mathematician has mastered the basics of counting up to 20 and does not confuse the sequence of numbers, start giving him small tasks to consolidate the skill. For example, ask your child to give you 14 buttons, 12 berries, 15 coins, etc.

    4

    Learning to count to 100

    It is best to learn to count to a hundred at a younger preschool age - in the period from 4 to 6 years. Everything here is not much more complicated than at the previous stage:

    • Initially, tell the child that there are numbers "30", "40", "50", "60", etc. up to "100", and also that there are ten tens in total. Be sure to mention that there are specific units between all tens, and provide your narrative with simple examples.
    • Take one day to study each ten, completing tasks similar to those for teaching counting to 20. In the evening of each day, spend 15-20 minutes reviewing the material. For clarity, you can first use household items or toys. If you notice that some information is not absorbed by the child very well, return to the beginning of the current topic.
    • Use didactic materials and educational games as auxiliary methods. Write down sequences of numbers and let your child look for missing or specific numbers that you have named.
    • Praise your child as often as possible. Avoid negative evaluative phrases, such as "You are not succeeding", "You did not complete the task", "You do not understand well", etc. Never compare your child with other children. Do your best to keep him motivated and positive.

    Using these simple methods, you can easily and quickly teach your child to count to one hundred. But in parallel with this, you need to start mastering mathematical operations, for a start - addition and subtraction (not the simplest numbers, but two-digit ones). To do this, we advise you to teach your child to count with a column.

    5

    Learning to count with a column

    You should start learning to count with a column, making sure that the little man understands the count to 100 well and understands the tens. If everything is fine, explain how single and multi-digit numbers are formed, and show how they are written. After that, convey to the child's consciousness that operations with numbers are performed bit by bit, i.e. with units and tens when counting in a column, they work separately.

    If you add up numbers that add up to more than ten, the child may initially be misunderstood. For example, you need to add "14" and "18". So, adding "4" and "8" and getting "12", you need to write down the second digit, and keep the first in mind, so that later you can add it to the sum of the first column of numbers. Those. "1" + "1" "2" + "1" (the unit that was in the mind) "3". As a result, in the first column we get "3", and in the second "2", which means "32". If suddenly the baby has difficulty keeping one number in his mind, make it easier for him to write it down over the first column. As the method is mastered, it is better to exclude auxiliary techniques.

    In fact, in mastering the ability to count in a column, a child should not have any problems. But you always need to be patient, and if necessary, explain the same thing several times as clearly as possible. And here it would be appropriate to mention the three main rules for teaching children to count.

    6

    3 Golden Rules for Teaching Children

    If you have the idea of ​​helping your child learn basic math skills in preschool, follow these rules:

    1. Set a specific time when you will study. Take into account that, firstly, you need to practice every day, secondly, at least half an hour a day, and thirdly, the duration of one lesson should not exceed 15-20 minutes. Otherwise, you will overload the child's brain, and this is fraught with rapid fatigue, loss of interest, and even a negative attitude towards classes in general, including a specific subject at school in the future.
    2. Systematically review the material covered in the context of new assignments. This means that you do not need to memorize “by heart” how many “3” + “5” will be, but regularly train already mastered skills, solving more difficult problems.
    3. At any hint that the child is not coping with tasks or does not understand something, do not be persistent. It would be smarter to return to simpler tasks, and after a while try again to solve complex ones. Even if you are not a specialist, you must show pedagogical professionalism, i.e. adjust to your child's mindset.

    This concludes the sixth lesson, and we wish you success in your endeavors. Apply the methods, tips and tricks that we have presented, come up with different options for games and activities, try new things and experiment - then you will certainly succeed.

    The next lesson we devoted to the study of the multiplication table. From it you will learn what and how to do so that the child learns it quickly, where to start, what to do so that it is remembered faster, and how to check progress. We will also give you some tips to help you avoid the most common mistakes.

    Test your knowledge

    If you would like to test your knowledge of the topic of this lesson, you can take a short test consisting of several questions. Only 1 option can be correct for each question. After you select one of the options, the system automatically moves on to the next question. The points you receive are affected by the correctness of your answers and the time spent on passing. Please note that the questions are different each time, and the options are shuffled.