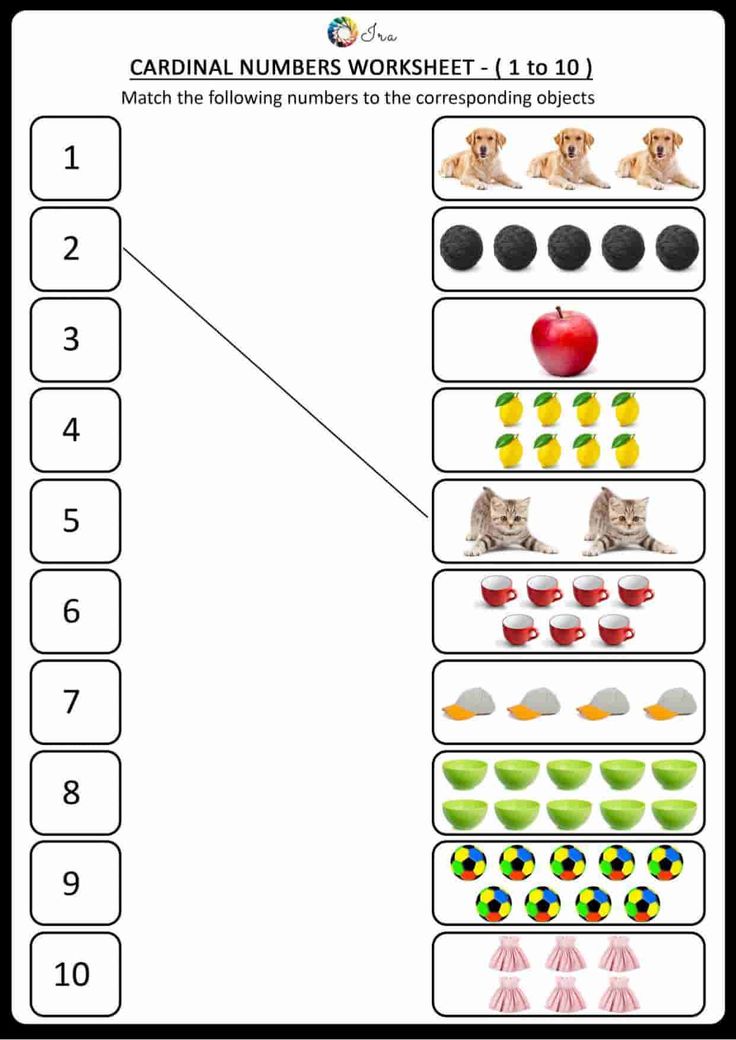
The cardinal numbers
What are Cardinal Numbers? Definition, List, Examples, Facts
What Are Cardinal Numbers?
Cardinal numbers are numbers that are used for counting real objects or counting things. They are also known as “counting numbers” or “cardinals.” We commonly use cardinal numbers or cardinals to answer the question starting with “How many?”
So, how to find the cardinal numbers around us? Let’s see an example.
Example:
How many dogs are in the given picture?
To know the total number of dogs, we need to count the dogs given in the image.
There are 8 dogs in all. Here, 8 is the cardinal number.
Related Games
Cardinal Numbers: Definition
The numbers that we use for counting are called cardinal numbers. They tell us the quantity of objects.
Cardinal Numbers Examples: 2 bananas, 5 suitcases, 100 points, a million dollars, etc.
Cardinal numbers do not include fractions or decimals. Cardinal numbers are natural numbers or positive integers. The smallest cardinal number is 1.
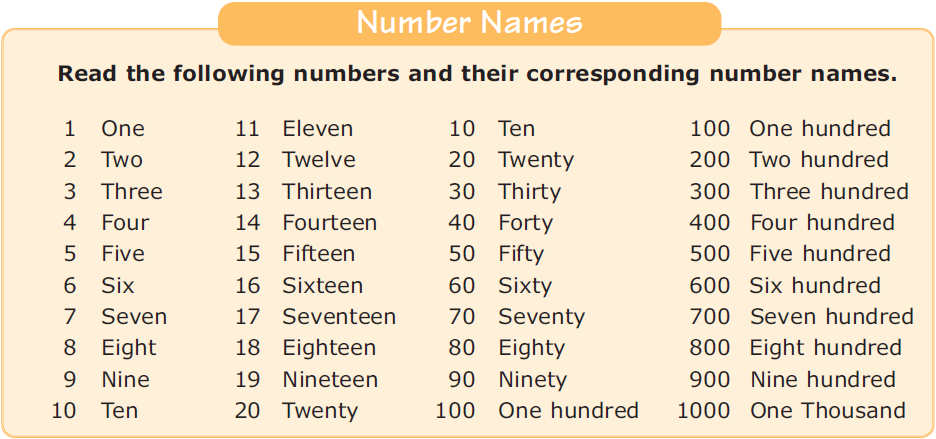
Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on.
The smallest cardinal number is 1.
If we count a bag filled with a million dollars, we get a cardinal number: “one million!”
Example:
Related Worksheets
Cardinal Numbers in Words
We can also write cardinal numbers in words. For the first 10 numbers, we can write the cardinal numbers as:
- 1 – One
- 2 – Two
- 3 – Three
- 4 – Four
- 5 – Five
- 6 – Six
- 7 – Seven
- 8 – Eight
- 9 – Nine
- 10 – Ten
List of Cardinal Numbers
Here’s a list of cardinal numbers up to 100, in figures and in words:
Cardinal Numbers as Multiples of 100:
We can count further and list a few larger cardinal numbers as well:
What Is Cardinality?
The cardinality of a group or a set represents how many elements or numbers are present in a group or in a set.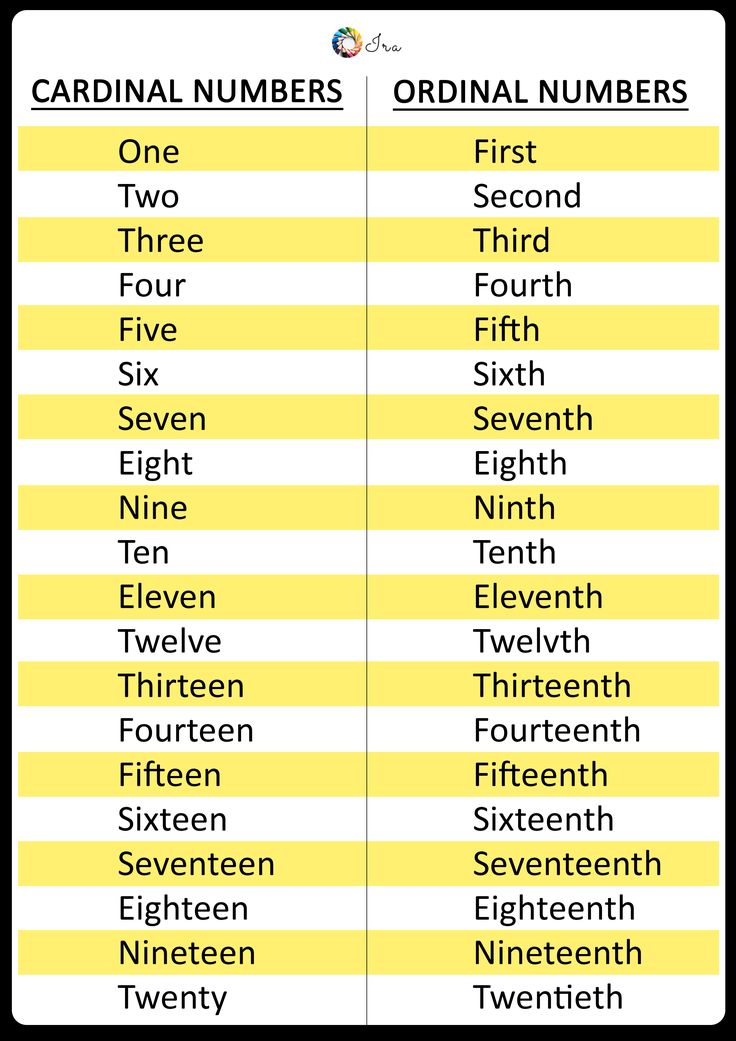
For example, if a pencil set has 10 pencils in it, then the cardinality of pencils is 10.
Cardinal Number of a Set
The number of elements in a set is known as the cardinal number of that set. If A is a finite set and it has N elements, then the cardinal number of set A is given by n(A) $=$ N.
Note: The cardinal number of an empty set is always zero.
For example, what is the cardinal number of a set if the set is defined as A $=$ {2, 5, 7, 9, 11, 15, 19, 22, 24}?
The cardinal number of set A is 9. Hence, n(A) $=$ 9
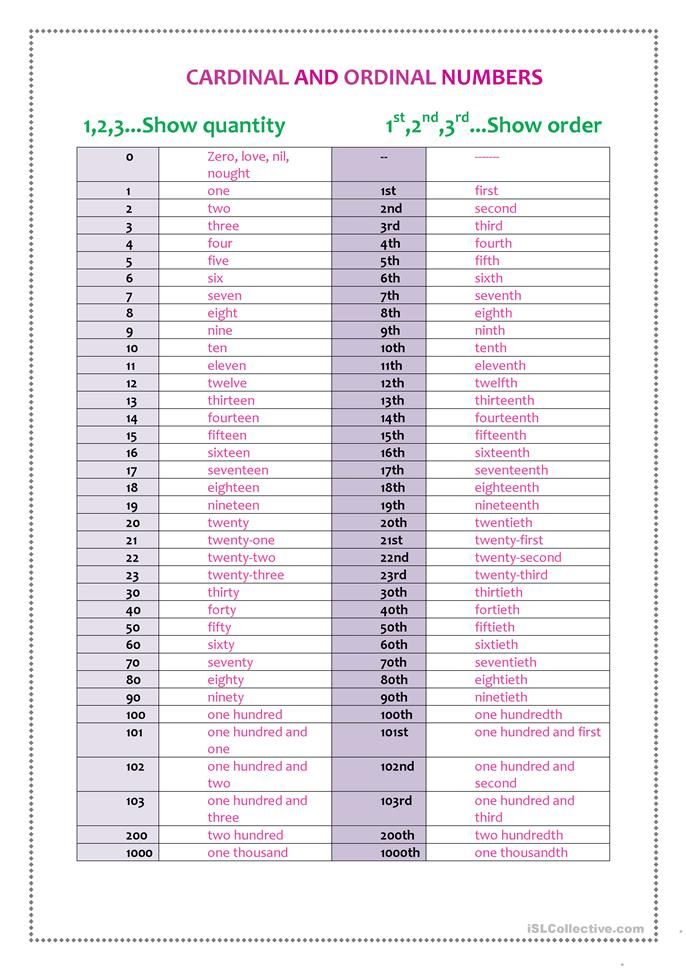
Cardinal Numbers vs. Ordinal Numbers
As we discussed, the cardinal numbers are used for counting. They include all the natural numbers. However, an ordinal number is a number that is used to represent the position or order of an object. Examples:
1st rank, 2nd in a queue, 3rd row, tenth floor, etc.
Ordinal numbers are used for ranking or ordering.
Here’s an example that explain the difference between cardinal and ordinal numbers:
In the image given above, we can see a group of 8 children on the picnic spot. Here, 8 represents the cardinal number.
In the above image, we can see the position of the kids in a running event. Here, first, second, third, fourth, fifth are ordinal numbers.
Difference between Cardinal Numbers and Ordinal Numbers
Nominal Numbers
Nominal numbers, as the name suggests, are used to name an object or a thing in a set of groups. They help us in the identification of objects. It is not used to represent the quantity or the position of an object.
For example:
- Social security number
- Zip code number
- Cell phone number
In the image given below, the numbers 22, 18 are nominal numbers since they are used on the jerseys to represent players or to identify players.
Conclusion
In this article, we learnt about the Cardinal Numbers.
Cardinal Numbers are the numbers used for counting numbers. To read more such informative articles on other concepts, do visit SplashLearn. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.
Solved Examples
1. Kathy has a list of numbers as shown: 10, 9, 7th, 22, Third, Five, 21st. Identify the cardinal numbers.
Solution: The cardinal numbers are used for counting. The cardinal numbers are 10, 9, 22 and Five.
2. Help Mark calculate the number of consonants in “INDEPENDENCE.” Also identify the number of alphabets used to form this word.
Solution: The consonants are alphabets other than vowels. The vowels are a, e, i, o and u. The number of consonants INDEPENDENCE are 7. The number of alphabets in the word INDEPENDENCE are 12.
3. Write the cardinality of the flowers in the vase.
Solution: There are 5 flowers in the vase. So, the cardinality is 5.
4. What is the position of the strawberry from the left?
Solution: The strawberry is at the second position from the left. Here, second is the ordinal number.
5. How many kites are there in all? What is a cardinal number here?
Solution: On counting, we get:
There are 8 kites. 8 is the cardinal number since we used it for counting.
Practice Problems
1
How many two-digit numbers are there?
89
90
91
92
Correct answer is: 90
The smallest two-digit number is 10 and the greatest two-digit number is 99.
From 1 to 99, there are 99 numbers. Out of them 9 numbers (1 to 9) are one-digit numbers.
So, we will subtract 9 from 99 to find the two-digit numbers.
Number of two-digit numbers $= 99 – 9 = 90$
2
The cardinality of the set A $= {12, 18, 23, 65}$ is
4
10
18
Cannot be defined.
Correct answer is: 4
Since the number of elements in the set is 4, the cardinality of the set is 4.
3
Which of the following is not a cardinal number?
23
Sixty-one
4th
77
Correct answer is: 4th
4th is not a cardinal number as it tells us about the position of something.
4
For which of the following are cardinal numbers used?
To find the number of objects
To identify the rank or order of something
To identify objects
All of these
Correct answer is: To find the number of objects
We use cardinal or natural numbers for finding the number of objects.
5
76 is a $\underline{}$ number.
Ordinal
Cardinal
Nominal
None of these
Correct answer is: Cardinal
76 is a natural number and hence, it is cardinal.
Frequently Asked Questions
Which is the smallest cardinal number?
The smallest cardinal number is 1.
Can cardinal numbers be negative?
No, cardinal numbers cannot be negative. They are positive integers or natural numbers, as we count the number of items starting from number 1, and then it goes up to infinity.
Is 0 a cardinal number?
No, we can not count 0 things.
Which is the biggest cardinal number?
The biggest cardinal number is infinity.
Can we do operations with the cardinal numbers?
Yes, we can do operations with the cardinal numbers. We can add, subtract, multiply, and divide the cardinal numbers.
Are all whole numbers cardinals?
All whole numbers are not cardinal numbers. 0 is a whole number but not a cardinal number as we can never say that the number of objects is 0.
What is the Cardinal Counting Principle?
When you count a number of objects in a group, the total number of items is the last word said while counting.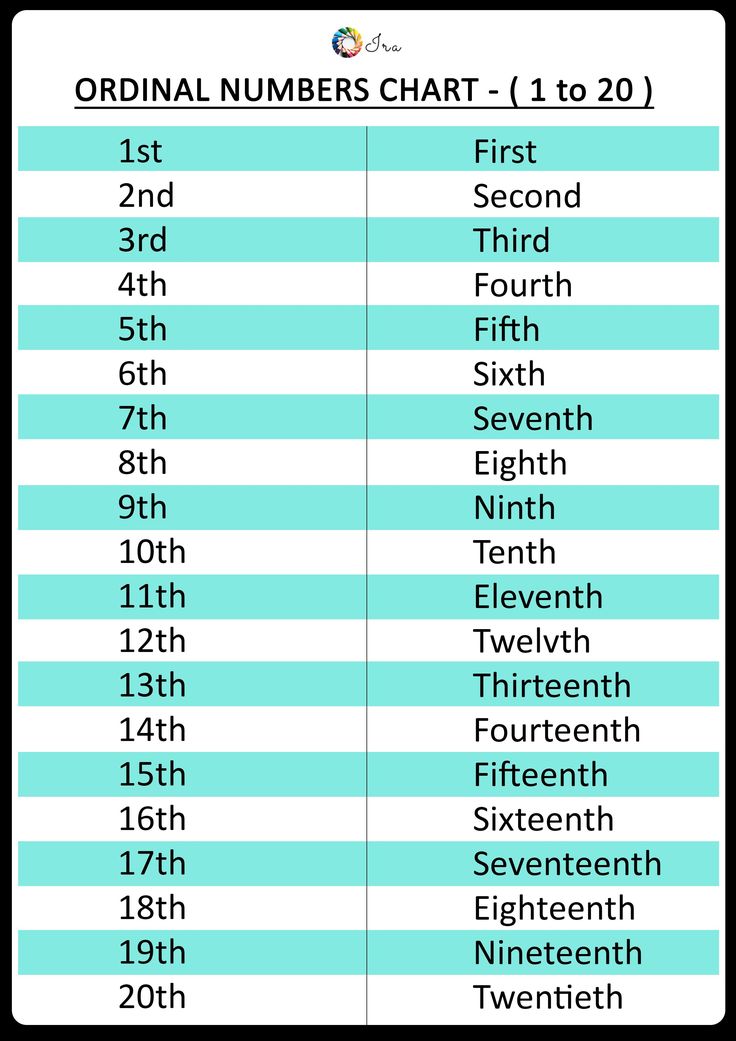
- Number
- First
- Ordinal Numbers
Cardinal Numbers - Meaning, Examples, Sets
Cardinal numbers are numbers that are used for counting. They are also known as natural numbers or cardinals. A set of cardinal numbers starts from 1 and it goes on up to infinity. We use cardinal numbers to answer the question "how many?". For example, how many students are going to the school picnic? The answer could be any number like 20, 23, 30, etc. So, all these numbers come in the category of cardinal numbers. In this article, we will explore the world of cardinal numbers and understand the difference between cardinal and ordinal numbers.
| 1. | What are Cardinal Numbers? |
| 2. | Difference Between Cardinal and Ordinal Numbers |
| 3. | List of Cardinal Numbers from 1 to 100 |
| 4. | Cardinal Numbers of a Set |
5. |
FAQs on Cardinal Numbers |
What are Cardinal Numbers?
A cardinal number describes or represents how many of something are present. Example 2 apples, 5 flowers, etc. It quantifies an object. It does not have values as fractions or decimals. Cardinal numbers are counting numbers, they help to count the number of items. Let's have a look at cardinal numbers examples. Ana wants to count the number of people standing in a queue at a billing counter. Can you help her? Ana started to count using Natural numbers.
Ana counted 1, 2, 3, 4, and 5. There are 5 people standing in a queue at the billing counter. Counting numbers are cardinal numbers! Now, Let's consider another example, Noah kept eight apples in a basket. The number eight denotes how many apples are there in the basket, irrespective of their order.
Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on.
The smallest cardinal number is 1 as 0 is not used for counting, so it is not a cardinal number.
Difference Between Cardinal and Ordinal Numbers
All the natural numbers are also referred to as cardinal numbers. Cardinal numbers are used for counting. While an ordinal number is a number that denotes the position or place of an object. Example: 1st, 2nd, 3rd, 4th, 5th, etc. Ordinal numbers are used for ranking. Here is an example that explains cardinal and ordinal numbers:
In the above image, we can see a team of 4 workers on the construction site. This is an example of cardinal numbers.
In the above image, we can see the position of the runners in the running event. First, second, third, and so on. This is an example of ordinal numbers. Let's discuss ordinal and cardinal number differences in the table below:
| Cardinal Numbers | Ordinal Numbers |
|---|---|
They are counting numbers that represent quantity. |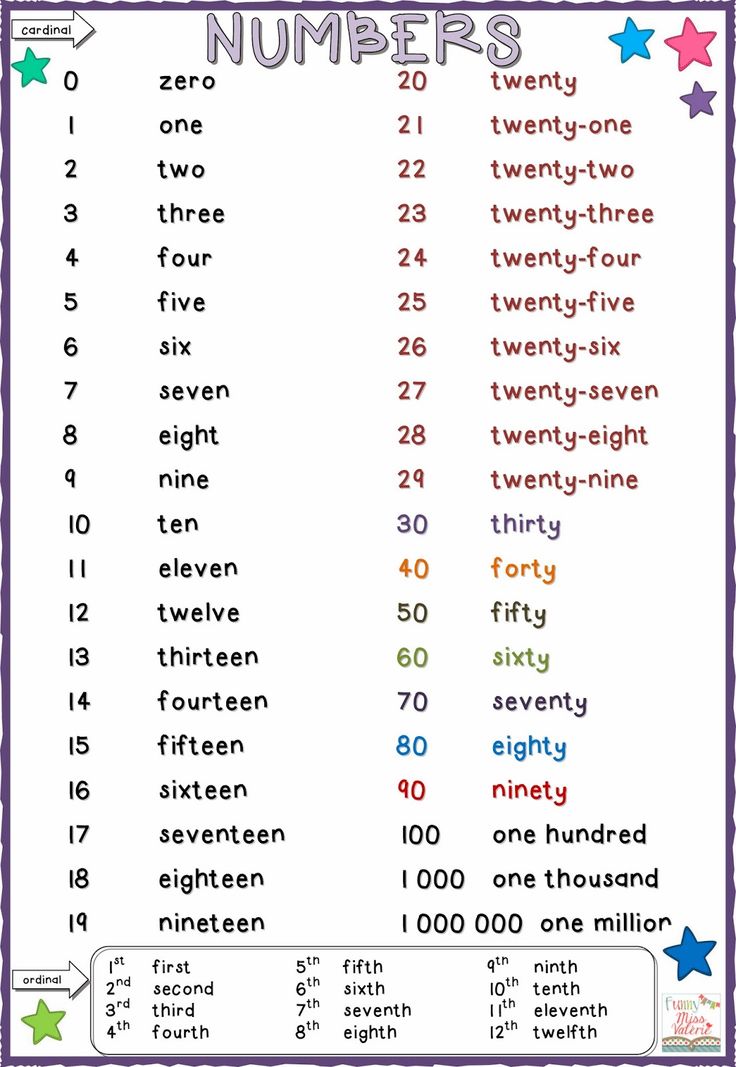
They are based on the rank or position of an object in a given list or order. |
| Cardinal numbers give us the answer of 'how many?'. | Ordinal numbers give us the answer of 'where'. For instance, where does the object lies in the list? |
| Examples are 1, 2, 3, 4, 5, 10, etc. | Examples are 1st, 2nd, 3rd, 4th, 5th, 10th, etc. |
List of Cardinal Numbers from 1 to 100
Given below are the basic and most important cardinal numbers, which form the base for other counting numbers.
| 1 - One | 6 - Six |
| 2 - Two | 7 - Seven |
| 3 - Three | 8 - Eight |
| 4 - Four | 9 - Nine |
| 5 - Five | 10 - Ten |
| 10 - Ten | 60 - Sixty |
| 20 - Twenty | 70 - Seventy |
| 30 - Thirty | 80 - Eighty |
| 40 - Forty | 90 - Ninety |
| 50 - Fifty | 100 - Hundred |
Given below is the list of all cardinal numbers from 1 to 100.
It will also help you to see how we write cardinal numbers in words like 21- twenty-one.
Cardinal Numbers of a Set
In the case of a set, the cardinal number is the total number of elements present in it. In other words, the number of distinct elements present in a set is the cardinal number of the set. The cardinal number of a set A is represented as n(A). For example, the cardinal number of set W = {1, 3, 5, 7, 9} is n(W)=5, as there are 5 elements in it.
Think Tank:
- Maria wrote January 1, 2020, as today’s date in her notebook. Does the number 1 in the date, represent a cardinal number?
- There are _______ people in the line ahead of me. I am the 7th person in the line.
Important Notes:
- Cardinal numbers help us to count the number of things or people in or around a place or a group.
- The collection of all the ordinal numbers can be denoted by the cardinal.
- Cardinal numbers can be written as words such as one, two, three, etc.
- Cardinal numbers tell how many items, whereas ordinal numbers show position or ranking.
Related Articles
Check out these interesting articles to know more about cardinal numbers and its related articles.
- Ordinal Numbers
- Whole Numbers
- Natural Numbers
- Difference Between Natural and Whole Numbers
Cardinal Numbers Examples
-
Example 1: Kate has a list of numbers as shown - 7, 8th, 10, Two, Fourth, 2nd. Identify the cardinal numbers.
Solution:
7, 10 and two help us in counting, whereas 8th, fourth and 2nd helps us in identifying the position. Thus, 7, 10, and two are cardinal numbers.
-
Example 2: Help Ryan, to calculate the number of vowels in "NUMBERS".
Also, identify the number of alphabets used to form this word.Solution:
(i) We know that a, e, i, o, and u are the vowels and in the given word u and e are used. Therefore, 2 vowels are used to form this number (2 is the required cardinal number).
(ii) We start counting from N to S, we see that "Numbers" has 7 alphabets in all. Therefore, a total of 7 alphabets are required to form the given word and here 7 is a cardinal number.
go to slidego to slide
Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations with Cuemath.
Book a Free Trial Class
Practice Questions on Cardinal Numbers
go to slidego to slidego to slide
FAQs on Cardinal Numbers
What is a Cardinal Number Example?
Cardinal numbers are used for counting. Some examples of cardinal numbers are 1, 2, 3, 4, 5, 10, 15, 20, 30, 40, 50, 100, etc.
In our daily life, we use cardinal numbers a lot. Even a small child uses this mathematical concept without knowing the term for it. They do count how many toys they have, how many people are there around them, how many friends they have, how many subjects do they study at school, etc.
What is the Smallest Cardinal Number?
The smallest cardinal number is 1 (one) as whenever we count, we always start from 1.
How do you Find Cardinal Numbers?
Cardinal numbers can be found by counting. We start by 1 and then go on as per the number sequence.
How is Cardinal Number Different from the Ordinal Number?
Cardinal numbers are numbers that represent the number of items(quantity) while ordinal numbers represent the rank or position of an item in the given list.
What is a Cardinal Number in Sets?
In set A, if there are a total of 25 elements then 25 is the cardinal number of set A represented by n(A).
Can Cardinal Numbers Negative?
No, cardinal numbers cannot be negative.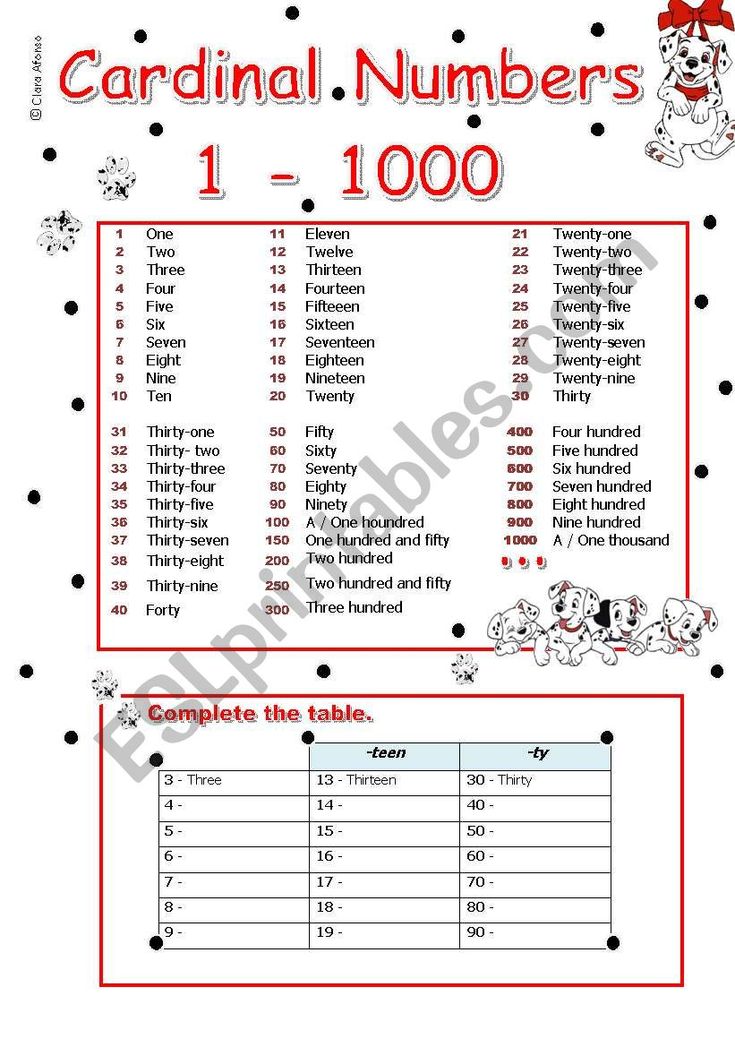
They are positive integers or natural numbers, as we always count the number of items starting from number 1, and then it goes up to infinity.
Is Zero a Cardinal Number?
No, 0 is not a cardinal number as cardinal numbers represent quantity, and 0 means nothing or no quantity.
What is the Biggest Cardinal Number?
There are infinite natural numbers. Therefore, there are as many cardinal numbers as natural numbers. There can be no generalization of the biggest natural number and so does for the biggest cardinal number.
cardinal number | it's... What is a cardinal number?
Aleph-zero, the smallest infinite cardinal.
Cardinal number or shortly cardinal in set theory is an object that characterizes the cardinality of a set. The cardinal number of any set A is denoted as | A | or Card A .
For a finite set A, the cardinal number |A| is a natural number, which means the number of elements of this set.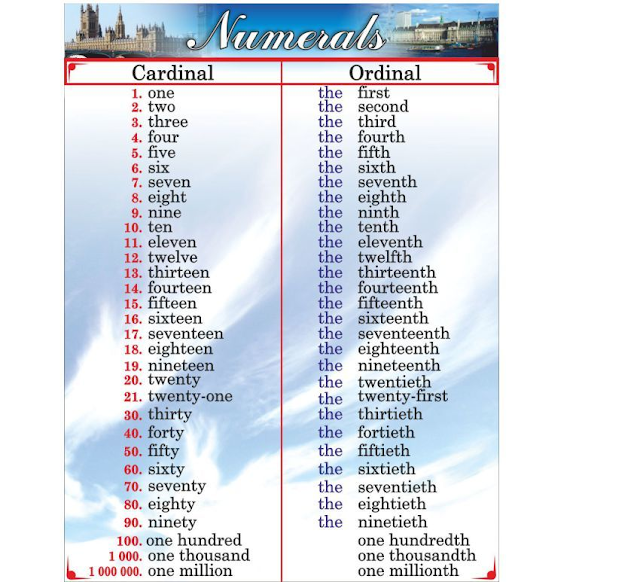
For infinite sets, the cardinal number is a generalization of the concept of the number of elements. nine0003
Although the cardinal numbers of infinite sets are not reflected in natural numbers, they can be compared. Let A and B be infinite sets, then the following four cases are logically possible:
- A ~ B and | A |=| B |.
- There is a one-to-one correspondence between the set A and some own subset B' of set B . Then we say that the cardinality of the set A is not greater than the cardinality of the set B and write | A |≤| B |.
- The set A is equivalent to some subset of the set B , and vice versa, the set B is equivalent to some subset of the set A , that is, A ~ B' ⊆ B0009 B ~ A' ⊆ A . According to the Cantor-Bernstein theorem, in this case, A ~ B is fulfilled, i.
e. | A |=| B |. - There is no one-to-one correspondence between set A and any subset of set B and there is also no one-to-one correspondence between set B and any subset of set A . It follows from this that the cardinalities of the sets A and B are not comparable.
However, deeper research in set theory has shown that, relying on the axiom of choice, it is possible to prove the impossibility of the existence of the fourth case.
Thus, the cardinalities of any two sets A and B are always comparable. That is, for cardinal numbers | A | and | B | arbitrary sets A and B , one of the three relations holds: | nine0009 A |=|B|, | A |≤| B | or | B |≤| A |. If | A |≤| B |, but the set A is not equivalent to the set B , then | A |<| B |.
|
Contents
|
Aleph numbers
Cardinal number of set N all natural numbers (and hence any countable set) are denoted by (read "aleph-zero").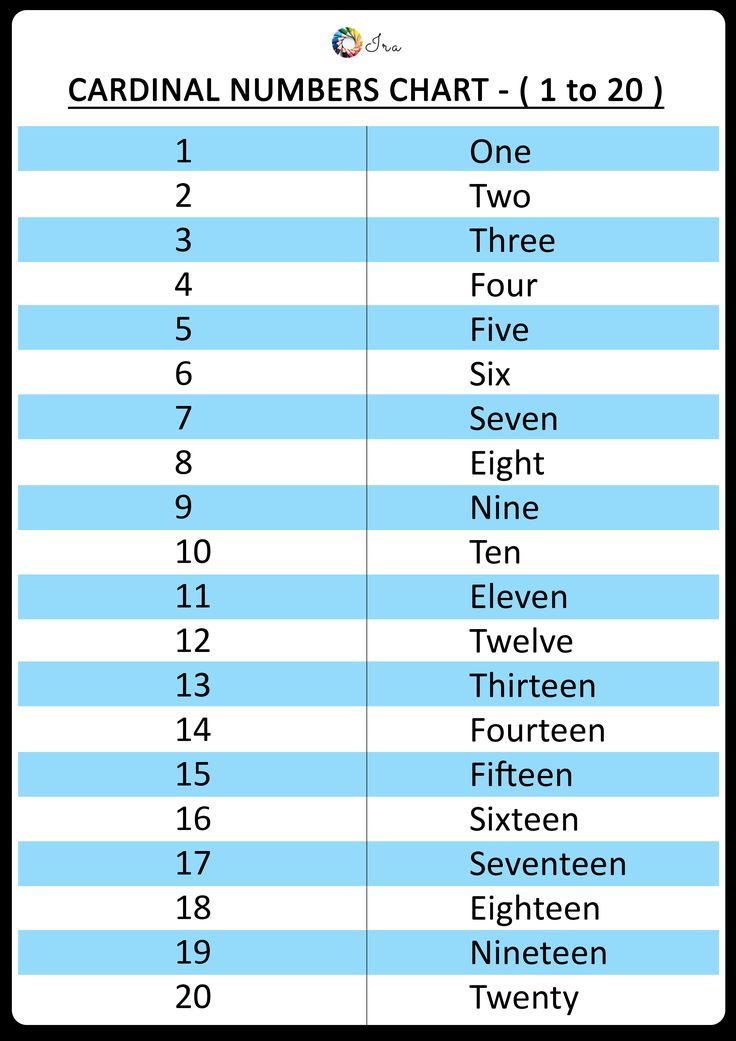
The cardinal number of continuum sets is denoted c or ("aleph-one"). The following cardinal numbers in ascending order denote Cantor proved that there is no set of the greatest cardinality, that is, there is no greatest cardinal number.
The Continuum Hypothesis
The Continuum Hypothesis states that there is no set whose cardinal number lies between the cardinal number of the set of natural numbers and the cardinal number of the set of real numbers , that is, < < . nine0003
See also
- Power of set
- Ordinal number
- Cantor-Bernstein theorem
- Continuum hypothesis
References
- Hans Hahn, Infinity , Part IX, Chapter 2, Volume 3 of The World of Mathematics . New York: Simon and Schuster, 1956.
- Paul Halmos, Naive set theory . Princeton, NJ: D. Van Nostrand Company, 1960. Reprinted by Springer-Verlag, New York, 1974. ISBN 0-387--6 (Springer-Verlag edition).
- Weisstein, Eric W. Cardinal Number at Wolfram MathWorld .
- Cardinality at ProvenMath formal proofs of the basic theorems on cardinality.
- Undergraduate Set Theory more proofs about cardinality - includes proof of infinite cardinal addition in Section 4.2.
ContentsPreface to the second Russian editionHow to use the book What is mathematics? Chapter I. Natural numbers § 1. Operations on integers 2. Representation of integers using written characters (numbering). 3. Arithmetic operations in non-decimal number systems. nine0221 § 2. Infinity of the system of natural numbers. Mathematical induction 2. Arithmetic progression. 3. Geometric progression. 4. The sum of the first n squares. 5. One important inequality. 6. Binomial theorem. 7. Further remarks on the method of mathematical induction. Supplement to Chapter I Theory of numbers 2.  Distribution of prime numbers. § 2. Comparisons 2. Fermat's theorem. 3. Quadratic residues. § 3. Pythagorean numbers and Fermat's last theorem § 4. Euclid's algorithm 2. Application to the fundamental theorem of arithmetic 3. Euler function. Once again about Fermat's theorem. 4. Continued fractions. Diophantine equations Chapter II. Mathematical number system § 1. Rational numbers 2. Emergence of need for rational numbers within mathematics itself. Generalization principle. 3. Geometric representation of rational numbers. § 2. Incommensurable segments. Irrational numbers, limits 2. Decimal fractions: finite and infinite. nine0221 3. Limits. Infinite geometric progressions. 4. Rational numbers and periodic decimal fractions. 5. General definition of irrational numbers by means of contracting segments. 6. Other methods for determining irrational numbers. Dekind's sections. § 3. Remarks from the field of analytic geometry 2.  Equations of straight and curved lines. § 4. Mathematical analysis of the infinite 2. Countability of the set of rational numbers and uncountability of the continuum. 3. "Cardinal numbers" by Cantor. nine0221 4. Indirect method of proof. 5. Paradoxes of the infinite. 6. Foundations of mathematics. § 5. Complex numbers 2. Geometric representation of complex numbers. 3. De Moivre's formula and roots from unity. 4. Fundamental theorem of algebra. § 6. Algebraic and transcendental numbers 2. Liouville's theorem and the construction of transcendental numbers. Supplement to chapter II. Algebra of sets 2. Application to mathematical logic. 3. One of the applications to the theory of probability. nine0221 Chapter III. Geometric constructions. Algebra of number fields Part 1. Impossibility proofs and algebra 1. Construction of fields and extraction of square roots. 2. Regular polygons. 3. 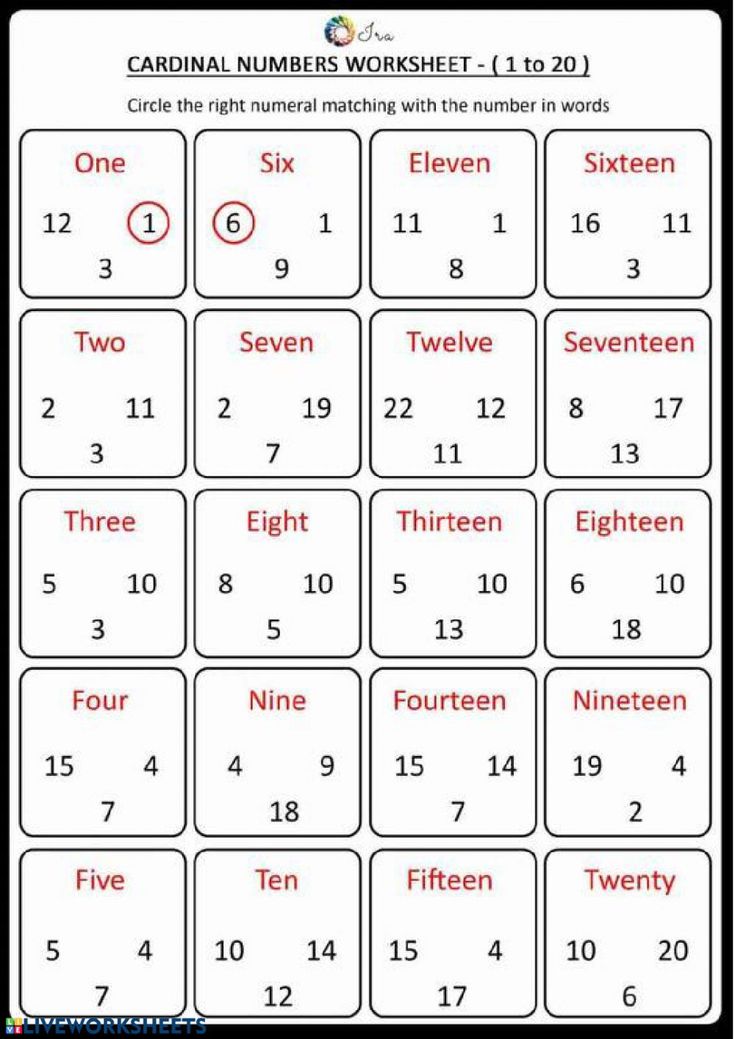 Problem of Apollonius. § 2. Numbers admitting construction and number fields 2. All numbers admitting construction are algebraic. § 3. Unsolvability of three classical problems 2. A theorem on cubic equations. 3. Angle trisection. 4. Regular heptagon. nine0221 5. Remarks on the squaring of the circle. Part 2. Various methods for performing constructions § 4. Geometric transformations. Inversion 2. Inversion properties. 3. Geometric construction of inverse points. 4. How to divide a segment in half and how to find the center of a given circle with a single compass. § 5. Constructions with the help of other tools. Constructions of Mascheroni with a single compass 1. Classical construction for doubling the cube. 2. Constructions with a single compass. nine0221 3. Drawing with various mechanical devices. mechanical curves. Cycloids. 4. Hinge mechanisms. Inversors Poselle and Garta. § 6. Another inversion and its applications 1.  Invariance of angles. Families of circles. 2. Application to the problem of Apollonius. 3. Repeated reflections. Chapter IV. Projective geometry. Axiomatics. Non-Euclidean geometries 1. Classification of geometric properties. Invariance under transformations. 2. Projective transformations. nine0221 § 2. Basic concepts 1. Group of projective transformations. 2. Desargues' theorem. § 3. Double relation § 4. Parallelism and infinity 2. Ideal elements and projection. 3. Double relation with elements at infinity. § 5. Applications 2. Two-dimensional proof of Desargues' theorem. 3. Pascal's theorem. 4. Brianchon's theorem. 5. Remark on duality. § 6. Analytical representation 2. Homogeneous coordinates. Algebraic foundations of duality. nine0221 § 7. Problems on constructions with the help of one ruler § 8. Conic sections and quadrics 2. Projective properties of conic sections. 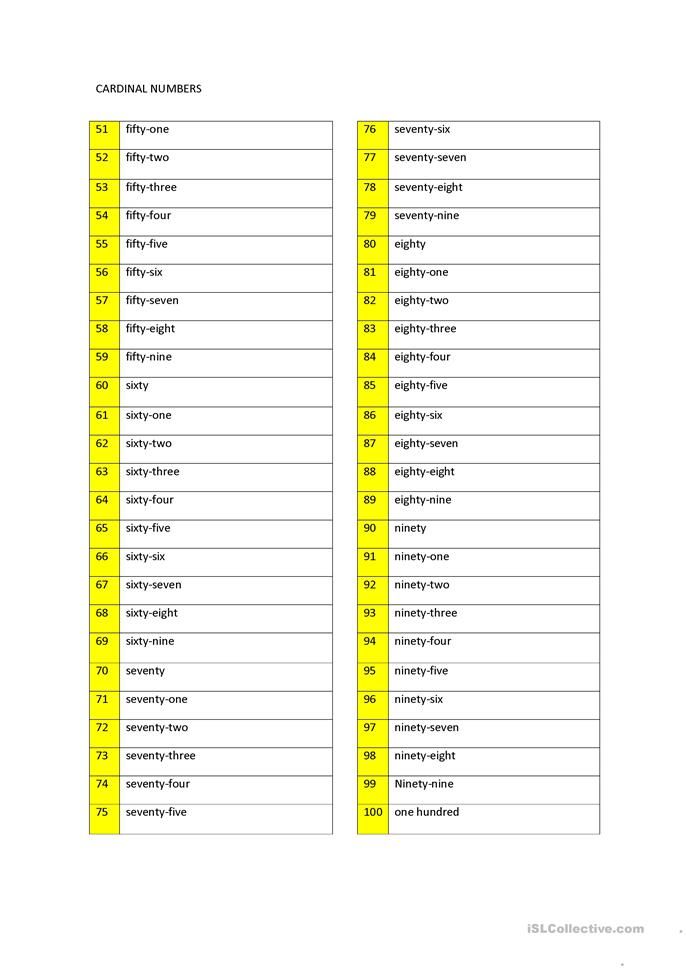 3. Conic sections as "ruled curves". 4. Pascal's and Brianchon's theorems for the general case of arbitrary conic sections. 5. Hyperboloid. § 9. Axiomatics and non-Euclidean geometry 2. Hyperbolic non-Euclidean geometry. 3. Geometry and reality. 4. Poincare model. 5. Elliptic or Riemannian geometry. nine0221 Application. Geometry in spaces of more than three dimensions Chapter V. Topology § 1. Euler's formula for polyhedra § 2. Topological properties of figures 2. Connection properties. § 3. Other examples of topological theorems 2. The problem of four colors. 3. The concept of dimension. 4. Fixed point theorem. 5. Knots. § 4. Topological classification of surfaces 2. Euler characteristic of a surface. 3. One-sided surfaces. nine0221 Appendix 2. Jordan's theorem for the case of polygons. 3. Fundamental theorem of algebra. Chapter VI. Functions and limits § 1.  Independent variable and function 2. Radian measure of angles. 3. Graph of a function. Inverse functions. 4. Complex functions. 5. Continuity. 6. Functions of several variables. 7. Functions and transformations. § 2. Limits 2. Monotone sequences. 3. Euler number e. 4. The number "pi" 5. Continued fractions. nine0221 § 3. Limits in continuous approximation 2. Remarks on the concept of limit 3. Limit sin x/x 4. Limits as x -> oo. § 4. Exact definition of continuity § 5. Two main theorems on continuous functions 2. Proof of Bolzano's theorem. 3. Weierstrass's theorem on extreme values. 4. Sequence theorem. Compact sets. § 6. Some applications of Bolzano's theorem 2. Application to a certain mechanical problem. nine0221 Addendum to chapter VI. Further examples on limits and continuity 4. Discontinuous functions as the limit of continuous ones. 5. Iteration limits. 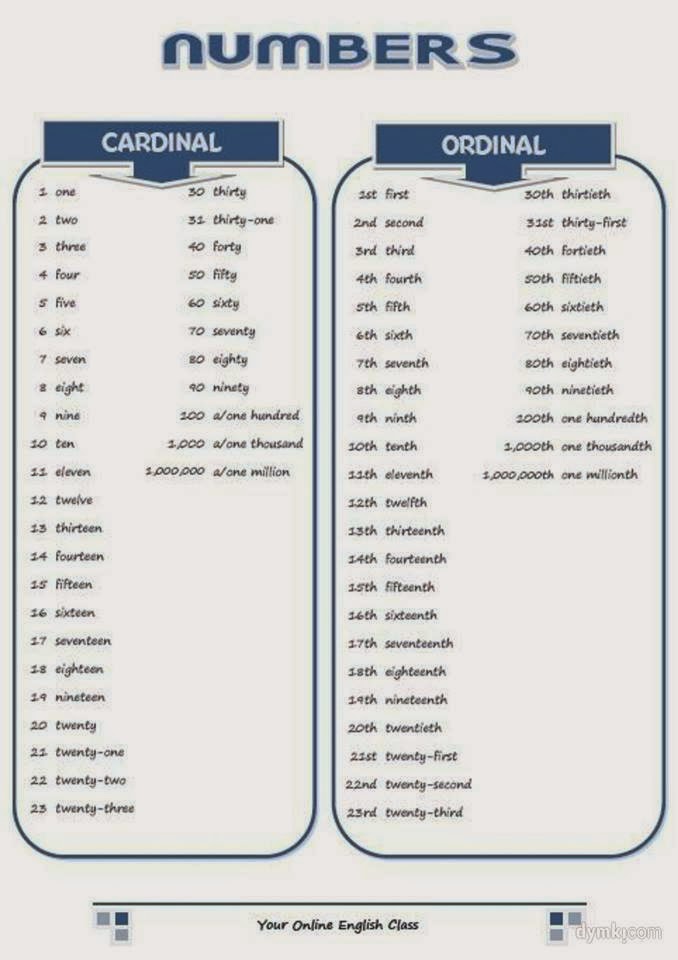 § 2. An example relating to continuity Chapter VII. Maxima and minima § 1. Problems from the field of elementary geometry 2. Heron's theorem. Extreme property of light rays. 3. Applications to triangle problems. 4. Properties of tangents to an ellipse and a hyperbola. Corresponding extremal properties. 5. Extreme distances of a point from a given curve. nine0221 § 2. The general principle to which extremal problems are subject § 3. Stationary points and differential calculus 2. Maxima and minima of functions of several variables. saddle points. 3. Minimax points and topology. 4. Distance of a point from a surface. § 4. Schwarz's triangle 4. Triangles formed by light rays. 5. Remarks concerning reflection and ergodic motion problems. § 5. Steiner's problem 2. Analysis of emerging alternatives. nine0221 3. Additional problem. 4. Remarks and exercises. 5. Generalization: the problem of the street network.  § 6. Extremes and inequalities 1. Arithmetic and geometric mean of two positive quantities. 2. Generalization to the case of n variables. 3. Least squares method. § 7. Existence of an extremum. Dirichlet principle 3. Extremal problems of elementary content. 4. Difficulties arising in more complex cases. § 8. Isoperimetric problem § 9. Extremal problems with boundary conditions. Connection between the Steiner problem and the isoperimetric problem § 10. Calculus of variations 2. Calculus of variations. Fermat's principle in optics. 3. Solution of the brachistochrone problem due to Jacob Bernoulli. 4. Geodesic lines on the sphere. Minimaxes. § 11. Experimental solutions of minimal problems. Experiments with soap films 2. Experiments with soap films. 3. New experiments related to the Plateau problem. niner. 5. The rules of "integral calculus". § 2. Derivative 2. Derivative as a limit.  
|
The book is written in a very accessible way and is a classic of the popular genre in mathematics. nine0003 
