What is number concept
Number System - Definition, Types, Conversion, Examples, Facts
What Are Numbers?
A number is an arithmetic value used to represent quantity. Hence, a number is a mathematical concept used to count, measure, and label. Thus, numbers form the basis of mathematics.
For example, this is 1 butterfly and these are 4 butterflies.
Related Games
History of Numbers
The inscriptions found at archaeological sites show that early humans used various symbols to show numbers. For example, ancient farmers, traders, and merchants used tally marks to show quantities. In tally marks, a standing line is drawn for each count and the fifth count is shown by striking off the four lines. This, however, was a tedious way and it was not feasible to show quantities.
Different ways of writing numbers were brought to use with the development of early civilizations. They used different symbols to show larger quantities. But even with these systems, it was not easy to show large quantities.
Around the seventh century, a decimal (or base ten) positional method, was perfected in India. This method used ten unique symbols to represent any number or quantity. These symbols are 0, 1, 2, 3, 4, 5 6, 7, 8, and 9.
This system was spread across Europe by the Arab merchants, scholars, and conquerors.
This system is called the Hindu–Arabic numeral system, and it remains the most common system for representing numbers to date.
Related Worksheets
Numbers in Everyday Life
Numbers are used everywhere around us. Your birthday has numbers that tell the day, month, and year you were born.
Numbers are used to keep track of time. We use clocks that show us time. We plan our day and events according to time.
Numbers are involved in buying and selling too. To count money and the units of an item, we use numbers.
Numbers are used for measurement. Temperature, weight, length, capacity, speed, distance, area, volume, and so on are measured using numbers.
Numbers play an important role in our body too. We have 2 eyes, 2 ears, 1 nose, 2 hands, 2 legs, and an adult body has 206 bones.
Our houses have numbers, bank accounts have numbers, and so do our cars, buses, trains, and flights.
Number Representation
- Digits 0-9
A number system is a writing system for denoting numbers using digits or symbols in a logical manner.
We use the digits from 0 to 9 to form all other numbers.
With the help of these digits, we can create infinite numbers.
For example, 121; 34,987; 2,987,633; 459,227,904; …
This number system using 10 digits is called the Decimal Number System.
- Alphabetical Form of Number
Number words are the alphabetical form of numbers. As the name suggests, these are numbers written in words.
For example:
1 One
2 Two
15 Fifteen
33 Thirty-three
- Symbolically, Using Numerals
Numerical symbols are numerals, such as Hindu-Arabic numerals (for example: 112, 415, 999) or Roman numerals (I, II, V, VIII).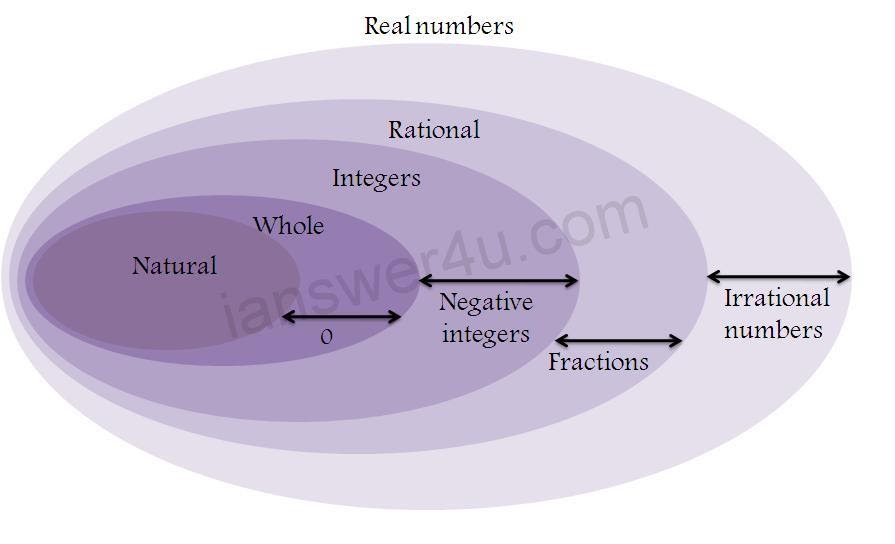
Cardinal Numbers and Ordinal Numbers
Cardinal numbers are counting numbers. The numbers that we use for counting are called cardinal numbers.
Cardinal numbers tell us how many things, items, or objects are there.
Example: 1, 2, 3, 10, 158
Ordinal numbers give us the exact position of a thing, item, or an object in the list. Ordinal numbers tell the position of an object rather than its quantity.
Example: 1st, 2nd, 3rd, 9th, 150th
Types of Numbers
Apart from the above, there exist other numbers, namely even and odd numbers, prime numbers, and composite numbers. These can be defined as follows:
Fraction and Decimal Numbers:
Solved Examples on Numbers
Example 1: Classify the given set of numbers as fractions or decimals.
7/12; 0.0008; 1.52; 100/10; 4 1/2; 7555.0
Solution:
Example 2: Write the numerator and denominator of given rational numbers.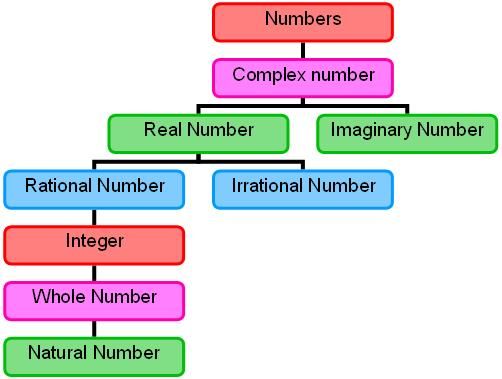
- 17/21 (b) 4/5 (c) 25/22
Solution:
Example 3: Write the numbers in words.
- 548
- 1,660
Solution:
- Five hundred and forty-eight.
- One thousand six hundred and sixty.
Practice Problems
1
How many odd numbers are there between 64 and 90?
11
12
13
14
Correct answer is: 13
65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89
2
Sum of the numbers of primes between 10 to 20 and 30 to 40 is
5
6
7
8
Correct answer is: 6
Prime numbers between 10 to 20 are 11, 13, 17 and 19 So, there are 4 prime numbers between 10 to 20. Prime numbers between 30 to 40 are 31 and 37 So, there are 2 prime numbers between 30 to 40. Sum = 4 + 2 = 6
Sum = 4 + 2 = 6
3
Four thousand eight hundred and eight in numeral form is written as:
4,880
4,808
4,800
48,008
Correct answer is: 4,808
4,000 + 800 + 8 = 4,808
4
What type of number is –5?
Natural number
Whole number
Integer
Correct answer is: Integer
–5 is a negative number, so it’s an integer.
Frequently Asked Questions
How do you find if a number is odd or even?
If a number is divisible by 2 with no remainder, then it is an even number. If a number is divided by 2 and leaves the remainder 1, then it is an odd number.
Is zero an even number?
When zero is divided by 2, the quotient is 0 and remainder is also 0. So, zero is an even number.
Can rational numbers be negative?
Yes, rational numbers are classified as positive, zero, or negative rational numbers.
Do fractions count as whole numbers?
Whole numbers do not include fractions or decimals.
What is number sense? Why is it important for maths mastery?
Editor’s Note:
This is an updated version of a blog post published on September 14, 2017.
Number sense is an important construct that separates surface level understanding from subject mastery. Find out how it affects mathematical fluency and how your learners can develop it.
So, what is number sense and why is it important for learners to develop this skill?
The construct of number sense refers to a child’s fluidity and flexibility with numbers. It helps children understand what numbers mean, improving their performance of mental mathematics, and giving them the tools to look at maths in the outside world and make comparisons.
How to spot number sense
Children develop number sense gradually over time and at different rates through exploring numbers, visualising them in a variety of contexts, and relating them in ways that are not limited by formal written methods.
You can track their progress by checking for the following:
- An awareness of the relationship between number and quantity
- An understanding of number symbols, vocabulary, and meaning
- The ability to engage in systematic counting — including notions of cardinality and ordinality
- An awareness of magnitude and comparisons between different magnitudes
- An understanding of different representations of number
- Competence with simple mathematical operations
- An awareness of number patterns including recognising missing numbers
Flexibility with number is key to number sense
Number sense is the ability to be flexible with numbers. It helps children understand both how our number system works, and how numbers relate to each other. Children who develop number sense have a range of mathematical strategies at their disposal. They know when to use them and how to adapt them to meet different situations.
What good number sense looks like
Good number sense helps children manipulate numbers to make calculations easier and gives them the confidence to be flexible in their approach to solving problems.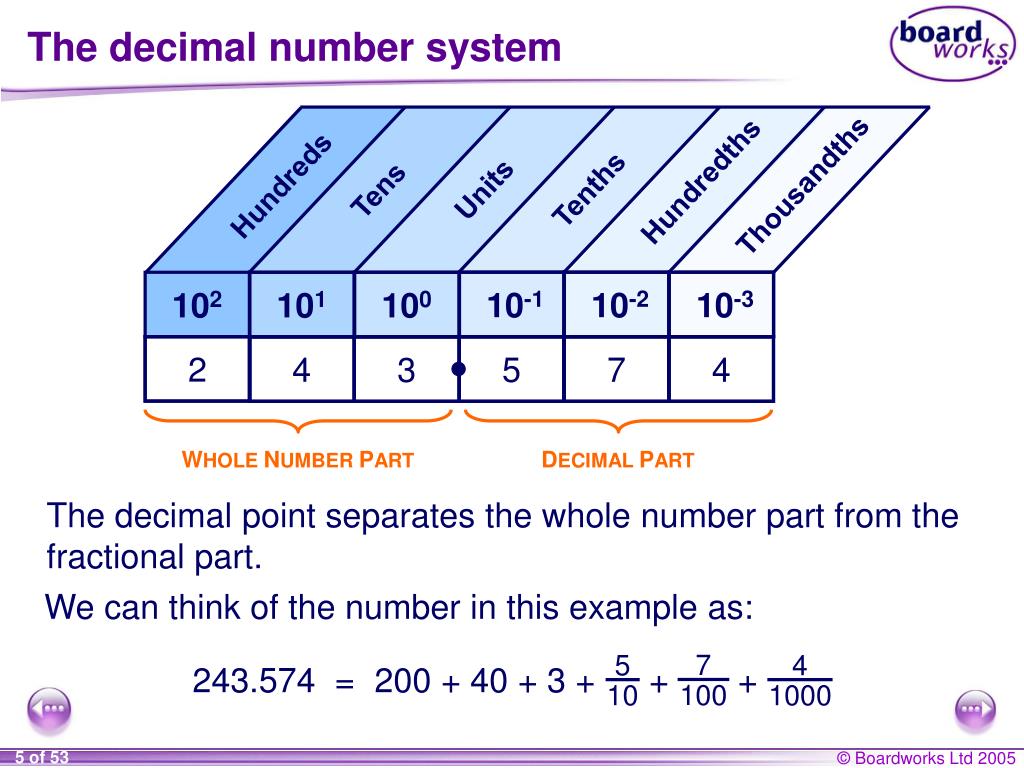
Children who develop number sense can assess how reasonable an answer is, and routinely estimate answers before calculating. They look for connections and readily spot patterns in numbers, which helps them predict future outcomes. They have several approaches to calculating and problem solving and can use and adapt these for new situations.
Children with good number sense enjoy playing with and exploring numbers and number relationships. As a result of these strategies, they can often find the most efficient solution to the problem.
What poor number sense looks like
Children with poor number sense tend to focus on procedure and will rely on methods that they feel secure with. They apply inefficient and immature strategies to calculations and fail to spot links and connections that could get them to the answer more quickly.
Often, children with poor number sense prefer to use pen and paper rather than working things out in their heads. They can be reluctant to estimate an answer before working it out and will generally accept whatever answer they get — without considering whether it is reasonable or not.
This was perfectly illustrated to me when a Year 5 child was trying to estimate the sum of two four-digit numbers before calculating the answer. She approached this task by calculating the answer and then giving an estimate. I asked her why she was doing it that way around and her reply was,
“It is much easier to find an estimate for the answer after you have worked out what the answer is.”
You have to admire her logic — if nothing else!
Children with poor number sense don’t enjoy maths and won’t spend time being creative with and exploring numbers. Ironically, they are doing a harder version of maths, that relies upon remembering and applying procedures, with little understanding of the underlying numerical concepts.
When does number sense develop?
Psychologists, Klein and Starkey (1988) found that we are born with a sense of number. They measured the focus time of babies looking at pictures of dots and discovered that when the number of dots changed the babies’ focus time changed.
These babies had appreciated a difference in numerical quantity.
Appreciating number quantity is a survival instinct. When our ancestors were out hunting and gathering they needed to be able to perceive danger. So, if one animal approached a couple of hunters, they saw this as an opportunity for a meal. However, if 10 animals approached them, they ran, or they became the meal!
We know that very young children can recognise the number of items in a group without having to count them. This is called subitising. Most people, but not all, can subitise up to six or seven items, when they are randomly arranged.
How learners can develop number sense
Number sense develops over time through opportunities to explore and play with numbers. Visualising numbers in different contexts, spotting relationships between numbers and predicting the patterns all contribute to good number sense.
definition, difference from a number, principle of formation, pronunciation, types
In this publication we will consider the definition of a number, list its main types and differences from a number, analyze the principle of formation of numbers and their pronunciation. The information presented is accompanied by examples for better understanding.
The information presented is accompanied by examples for better understanding.
- Definition of a number
- Differences between numbers and numbers
- The principle of the formation of numbers
- Pronunciation of numbers
- Numbers 1 to 20
- Dozens and hundreds
- 10 degrees
- Types of numbers
Definition of the number
The number is a quantitative characteristic of something. Used for counting, marking, measuring quantities, etc. Previously, dashes were used to denote numbers, but this method was extremely inconvenient for writing large values. Imagine how long it would take to draw dashes to write, for example, the number 745.
With the development of science and mathematics in particular, decimal number system was invented, containing the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, which are called Arabic. By the way, this system is used to this day and is the most common.
By the way, this system is used to this day and is the most common.
Differences between numbers and numbers
- The most obvious thing is that numbers are made up of numbers.
- A digit is a symbol, and a number is a quantitative abstraction.
- The number of numbers is unlimited, i.e. there are countless of them. At the same time, there are only 10 digits (listed above).
How numbers are formed
Ten digits can be used to write any natural number. Depending on how many digits are in a number, it can be:
- single digit - consists of one digit (for example: 2, 6, 7). The smallest single digit is one, the largest is 9.
- two-digit - consists of two digits (for example: 14, 52, 60, 78, etc.). The smallest two-digit number is 10, the largest is 99.
- three-digit - contains three digits (for example: 184, 211, 306, 612, etc.). The smallest three-digit number is 100, the largest is 999.
- four-digit, five-digit or, in other words, multi-digit (for example: 2048, 51947, 984871, etc.). In accordance with the name, such numbers consist of four, five, six or more digits.
Examples:
0071 “58” . That is, we arrange the numbers according to the corresponding digits:
- “8” - in units;
- "5" - in tens.
2. To write down the number “six hundred and twenty six” , we need only two digits - “6” and “2” , despite the fact that it is three-digit:
- “6” - in units and hundreds;
- "2" - in tens.
i.e. it turns out “626” .
Use of a comma
Not only numbers, but also commas (in some countries - periods) can be used to write numbers. This is done to separate the integer and fractional parts. For example:
- 120.
 5
5 - 306.71
- 221.409
The definition, notation, pronunciation and properties of decimal fractions are discussed in detail in a separate publication.
Pronunciation of numbers
Numbers 1 to 20
all digits of each class are pronounced in turn with the addition of the name of the class itself (from the oldest to the youngest), with the exception of the first class.
Examples:
- 65 - “sixty-five”;
- 247 - “two hundred and forty seven”;
- 1 518 – “one thousand five hundred and eighteen”;
- 25 814 – “twenty five thousand eight hundred fourteen”;
- 450 627 – “four hundred and fifty thousand six hundred twenty-seven”;
- 2 393 026 - “two million three hundred ninety-three thousand twenty-six”.
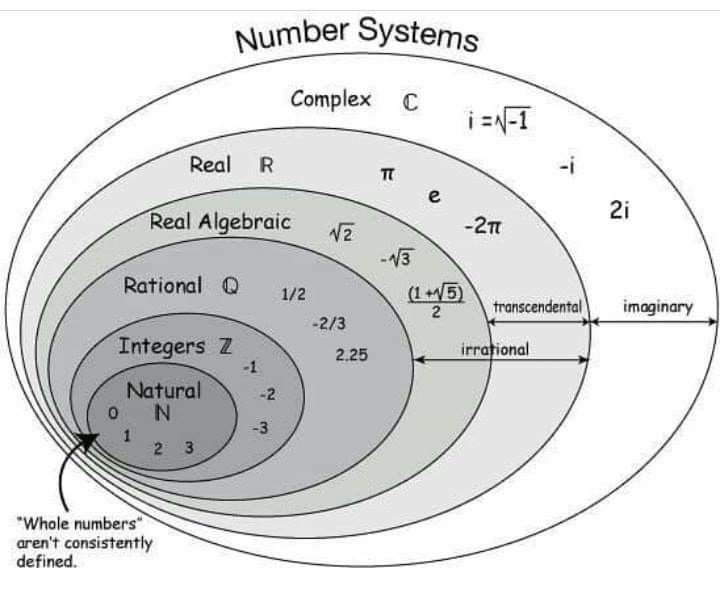
Types of numbers
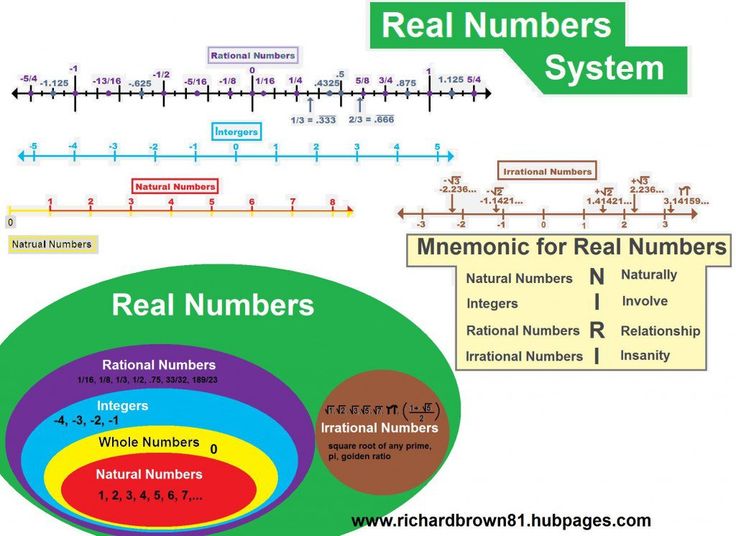
- Natural - all positive numbers that we use for counting (2, 19, 56, 478, 2048, etc.). Zero is not a natural number.
- Prime numbers are natural numbers that are only divisible by one and itself without a remainder: 2, 3, 5, 7, 11, etc.
- Compound - numbers that have three or more divisors.
- The integers are positive (greater than zero) and negative (less than zero) numbers that do not have a fractional part.
- Even - integers that are divisible by two without a remainder: 2, 4, 6, 8, 10, 12, etc.
- Odd - integers that are not divisible by two without a remainder: 15, 21, 37, 41, etc.
- Real – rational and irrational numbers.
- Rational - numbers that can be represented as an ordinary fraction.
- Irrational - infinite non-repeating decimal fractions that cannot be represented as ordinary ones.

The concept of the number and number of the first ten
1
-
Main concepts.
-
unambiguous numbers.
-
Order following numbers V row.
-
Compound unambiguous numbers.
-
Number 0.
-
Comparison numbers.
-
Number 10.
whole non-negative numbers are called natural in connections with the fact that they were invented by mankind for element counting real sets (animals, people, various items) and also to indicate the results measurement process (length, mass, capacity, time, area.).
So thus distinguish the number as result counting elements of the set and number as result measurement values (length, mass, time).
Alternative elementary math programs classes differ mainly in the way acquaintance of the child with these characteristics of the number.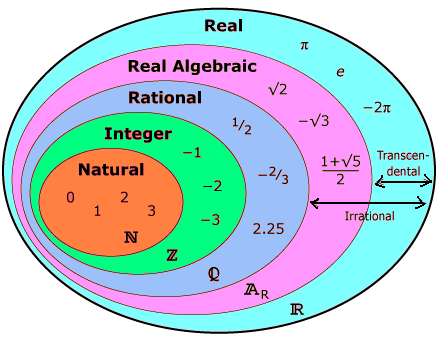
How and many mathematical concepts, the concept natural number arose from the needs of practice. Already in ancient times had to be compared various sets.
the simplest way of comparing sets was establishing a one-to-one correspondences between sets, i.e. education pairs of elements from both sets. If such correspondence took place, then the sets were considered equal (all pairs - complete).
If one-to-one correspondence established between elements of one set and only part of the elements of the second sets (some elements of the second sets remained
At this clearly shows that there are no pairs to count the needs left without a pair (“extra”) figures will show which there were more (and how much more).
So time for comparison began to be used intermediary sets (fingers, pebbles, knots ...) - they are called "numeric figures"; at the next stage as a result of the process abstraction from nature of the intermediary sets appeared number concept: one, two three.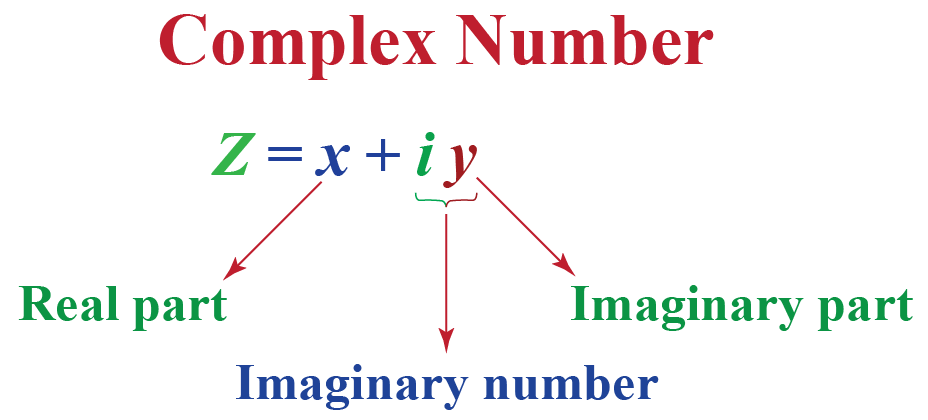
The science, studying numbers and actions with them called "arithmetic" (from Greek an1ito8 - number).
number — is quantitative characterization of the set items (groups).
Natural the numbers stand for when counting real items. Should remember that the number itself does not depend from character and properties of objects of a set, i.e. one and the same number can symbolize any number of objects character.
Each group (set) can be characterized only one number (and if, when repeated recalculation of objects it turns out another result, it means counting error).
Digit — is a character representing a number in a letter. Number we we call and hear. We see the figure, we write and call.
Numbers have a different image. Commonly used numbers, which are called Arabic (even though they have Indian origin): 1,2,3,4,5,6,7,8,9 and Roman: I, II, III, IV, V, VI, VII, VIII, ix, X.