Math concepts list
Branches, Fundamentals, Important Topics, Preparation Tips
Math is the science of quantity, pattern, order, structure and relation that has continuously evolved from basic practices of counting, measurements and symmetric study of shapes. It primarily involves applying logical reasoning and quantitative computation to find optimal solutions to problems. It has been worldwide recognized as an indispensable computational tool in the field of engineering, biology, medicine and natural sciences.
Math As A Subject
Math as a subject is an important part of the curriculum that plays a significant role in shaping a child’s future. It involves studying many useful concepts and topics relevant to practical life. Although math is an interesting subject, students often find it boring and complex due to the way it is taught conventionally. Cuemath helps students to explore and understand fundamental concepts in a fun and intuitive manner.
Fundamentals of Math
Fundamentals of math are the basic building blocks that help students form a solid mathematical foundation. Math learning entirely relies on the understanding of these fundamental concepts. If children lack the basic understanding of division or subtraction, then algebra automatically becomes confusing for them. Therefore, it is imperative that children must have a crystal clear knowledge of all fundamentals of math.
- Addition and Subtraction of Whole Numbers
- Multiplication and Division of Whole Numbers
- Exponents, Roots, and Factorization of Whole Numbers
- Introduction to Fractions and Multiplication and Division of Fractions
- Addition and Subtraction of Fractions, Comparing Fractions, and Complex Fractions
- Decimals and Fractions
- Ratios and Rates
- Techniques of Estimation
- Measurement and Geometry
- Signed Numbers
- Algebraic Expressions and Equations
Branches of Mathematics
Mathematics involves complex studies of interlinked topics and several concepts that overlap each other. Generally, it can be categorized into the following branches:
Generally, it can be categorized into the following branches:
Arithmetic
Arithmetic is the most basic branch of mathematics that deals with the elementary aspects of numbers, mensuration and numerical computations. This term is derived from the Greek word ‘arithmos’ which means number. It generally involves studying numbers and their relationships to solve problems that include the operations of addition, multiplication, subtraction, division, extraction of roots and raise to power.
Algebra
Algebra is an important and ancient branch of math that covers basic operations and symbols to represent numbers in formulas and equations. The word Algebra means the science of restoring and balancing. Learning algebra enables students to understand many real-life phenomena around them. It is a symbolic representation of numbers and how they work together to provide structure to equations. It forms the basis for advanced study in many fields like science, medicine, engineering, etc. It allows mathematicians to write formulas and solve maths problems more efficiently.
It allows mathematicians to write formulas and solve maths problems more efficiently.
Geometry
Geometry is the branch of math which deals with computation of various dimensions of solid shapes including height, width, area, volume, perimeter and angles. It has several useful applications from the construction of homes to interior designs.
Trigonometry
Trigonometry is an important branch of math that involves studying the relationship between angles, lengths, heights and distance. The applications of trigonometry can be found in many spheres including architecture, physics, surveying, electronics, satellite navigation, astronomy and engineering.
List of Branches of Maths
Important Math Topics
A thorough understanding of all important math topics will benefit students throughout their lifetime. Some of the essential math concepts that students must have an in-depth understanding of are based on the topics listed below.
- BODMAS Rule
- Prime and Composite numbers
- HCF and LCM
- Basic Menstruation
- Divisibility Rules
- Decimal and Fractions
- Ratio and Proportion
- Three-dimensional shapes
- Geometry
- Probability
Math Calculators
Students often find math challenging due to complex mathematical calculations. Math Calculators are handy tools to resolve all such problems. It makes calculations simple and quick. With the use of math calculators, calculations ranging from elementary arithmetic operations to complicated equations can be solved within a few seconds.
List of important calculators for students to solve problems quickly and get accurate solutions.
Important Math Formulas
Math formulas are expressions created after several years of research to help solve problems easily. Performing simple numerical operations like addition, subtraction and division are easy. However, to solve algebraic expressions, and other complex operations we use mathematical formulas. These are quite useful in obtaining the answers precisely. Cuemath provides formulas for each math topic along with the illustrated steps of equations for students to understand them logically.
However, to solve algebraic expressions, and other complex operations we use mathematical formulas. These are quite useful in obtaining the answers precisely. Cuemath provides formulas for each math topic along with the illustrated steps of equations for students to understand them logically.
List of important formulas that students must learn and memorize.
Tips And Tricks To Learn Math Fast
Although math is a vast subject there are some tips and tricks to learn math fast. These tips and tricks will help students improve along their math journey.
Clear All Basic: The first and foremost step in learning mathematics is to clearly understand all basics. It will not only allow you to learn math faster but will also help in establishing links between various math topics.
Set Objectives: After clearing all basics, set goals for what you need to focus on. Once you understand your objective, start working on it. Explore various resources that can help you improve and get well versed in those topics.
Practice Daily: Math requires daily practice, implementing a proper study routine will help in grasping concepts better.
Take Guidance: Heading in the right direction is necessary as it will ensure good results. Consider taking help from your teacher or a math tutor if you feel doubtful about topics and concepts.
FAQs on Math
What Exactly is Math?
Math is the science involving numbers, shapes and patterns which is present in almost everything around us. It helps us to derive analytical solutions to practical problems. It is applied in various fields such as engineering, finance, physical science, etc. It has a great impact in every domain of our life and we can find many mathematics applications around us.
How to Get Better at Math?
Getting better at math requires enforcing a study routine and analyzing mistakes. Students must try to understand and rectify their mistakes through daily practice. Doing so will also help them clear all their doubts.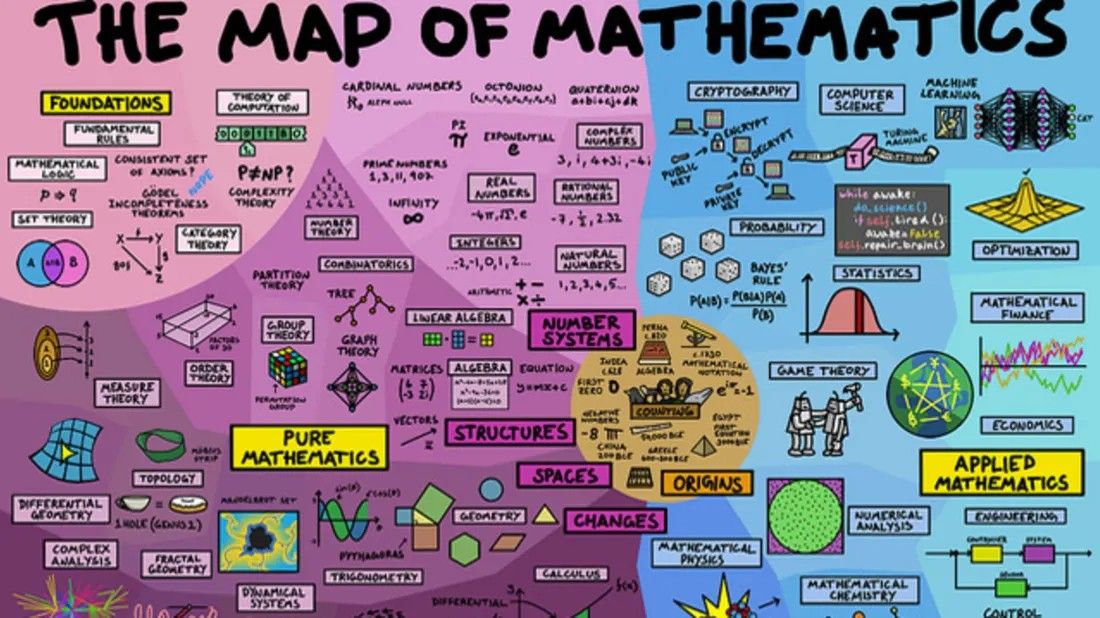 Students with better mathematical abilities achieve higher academic success. Thus, it is crucial to cultivate math interest in children at an early age. Cuemath’s visually-enriched math concepts enhance a child’s interest in mathematics and make it easier to learn the subject.
Students with better mathematical abilities achieve higher academic success. Thus, it is crucial to cultivate math interest in children at an early age. Cuemath’s visually-enriched math concepts enhance a child’s interest in mathematics and make it easier to learn the subject.
Why is Math Important in Our Daily Life?
Math is highly important in our daily life as there are several applications of mathematics in real-world situations. Statistics or probability theory are examples of applied maths.
What are the Fundamentals of Mathematics?
Fundamentals of mathematics are the building blocks for a solid math foundation. Students must possess a clear knowledge of all the fundamentals of mathematics to study advanced mathematical concepts. These fundamentals of mathematics are given below.
- Addition and Subtraction of Whole Numbers
- Multiplication and Division of Whole Numbers
- Exponents, Roots, and Factorization of Whole Numbers
- Introduction to Fractions and Multiplication and Division of Fractions
- Addition and Subtraction of Fractions, Comparing Fractions, and Complex Fractions
- Decimals and Fractions
- Ratios and Rates
- Techniques of Estimation
- Measurement and Geometry
- Signed Numbers
- Algebraic Expressions and Equations
How many Branches of Mathematics do we Have?
The branches of mathematics can be broadly categorized as:
- Arithmetic: Arithmetic involves studying numbers and their relationships to solve problems that include the operations of addition, multiplication, subtraction, division, extraction of roots and raise to power.

- Algebra: Algebra is the symbolic representation of numbers that provides structure to equations. It forms the basis for advanced study in many fields like science, medicine, engineering, etc.
- Geometry: Geometry is the calculation of various dimensions of solids including height, width, areas, volumes, perimeter and angles. It has many practical applications in architecture and other fields.
- Trigonometry: trigonometry deals with the study of the relationship between angles, lengths, and heights. The applications of trigonometry can be found in many spheres including architecture, physics, surveying, electronics, satellite navigation, astronomy and engineering.
What are the Most Important Math Topics?
Some of the most important math topics are prime numbers, composite numbers, BODMAS rule, geometry, probability, divisibility rules, HCF, LCM, three-dimensional shapes, basic menstruation, decimal, fractions, ratio and proportion. An in-depth understanding of all important math topics will enable students to score well in exams.
An in-depth understanding of all important math topics will enable students to score well in exams.
How Math is Used in Sports?
Math is used in sports to accumulate data, study conditions and generate performance statistics which are considered for planning and optimizing the training session. The data collected in these mathematical calculations is also helpful for taking strategic decisions based on the team’s performance.
How Maths is Related to Other Subjects?
Math is related to other subjects, especially chemistry, physics, computer science and engineering. In chemistry, mathematics is used to write and balance equations. In physics. It is applied to calculate mass, velocity and acceleration. In computer science, math is used to build algorithms and solve problems.
Main Branches of Mathematics Tree | PDF | Pure & Applied
Shakuntala Devi rightly said that without mathematics, there is nothing you can do. To explore more, let’s first know the 5 main branches of mathematics, i. e. Algebra, Number Theory, Arithmetic and Geometry. In the past 2 decades or so, our modern world has introduced more branches like Probability and Statistics, Topology, Matrix Algebra, Game Theory, Operations Research derived from these oldest branches of math. Breaking the myth of mathematics being called boring, we bring to you all about branches of mathematics with their list, tree and career options!
e. Algebra, Number Theory, Arithmetic and Geometry. In the past 2 decades or so, our modern world has introduced more branches like Probability and Statistics, Topology, Matrix Algebra, Game Theory, Operations Research derived from these oldest branches of math. Breaking the myth of mathematics being called boring, we bring to you all about branches of mathematics with their list, tree and career options!
Check Out: Vedic Maths
Tree of the Branches of Mathematics
Branches of MathematicsMain Branches of Mathematics
YouTube: DOS- Domain of ScienceMathematics is a complex area of study and comprises interlinked topics and overlapping concepts. Additionally, extensive analysis of the branches of mathematics helps students in organizing their concepts clearly and developing a strong foundation. Being aware of the differences and uniqueness of branches of mathematics helps in methodically studying various concepts of maths and also guides students in deciding the branch they would like to pursue as a career.
Here are the main branches of mathematics:
- Foundations
- Arithmetic
- Algebra
- Geometry
- Trigonometry
- Calculus
- Probability and Statistics
- Number Theory
- Topology
Below explained are the important branches of mathematics with their unique features and distinct concepts. These branches are important for laying a strong foundation for mathematics.
Fun Fact: -40 °C is equal to -40 °F.
Arithmetic
“Arithmetic must be discovered in just the same sense in which Columbus discovered the West Indies, and we no more create numbers than he created the Indians.”
– Bertrand Russell
Arithmetic is one of the most basic branches of mathematics and deals with numbers and their applications in many ways. Addition, subtraction, multiplication, and division are used as the basic groundwork to solve a large number of questions and progress into more complex concepts like exponents, limits, and many other types of calculations. This is one of the most important branches because its fundamentals are used in everyday life for a variety of reasons from simple calculations to profit and loss computation.
Addition, subtraction, multiplication, and division are used as the basic groundwork to solve a large number of questions and progress into more complex concepts like exponents, limits, and many other types of calculations. This is one of the most important branches because its fundamentals are used in everyday life for a variety of reasons from simple calculations to profit and loss computation.
Word Problems on Arithmetic Operations
Arithmetic Reasoning
Algebra
“The algebraic sum of all the transformations occurring in a cyclical process can only be positive, or, as an extreme case, equal to nothing.”
– Rudolf Clausius
A broad field of mathematics, algebra deals with solving generic algebraic expressions and manipulating them to arrive at results. Unknown quantities denoted by alphabets that form a part of an equation are solved for and the value of the variable is determined. A fascinating branch of mathematics involves complicated solutions and formulas to derive answers to the problems posed.
A fascinating branch of mathematics involves complicated solutions and formulas to derive answers to the problems posed.
Algebra Questions
Algebra Formulas
Fun Fact: The word “mathematics” only appears in one Shakespearean play, “The Taming of the Shrew”.
Geometry
“The description of right lines and circles, upon which geometry is founded, belongs to mechanics. Geometry does not teach us to draw these lines, but requires them to be drawn.”
-Isaac Newton
Do you often wonder about the shapes and sizes of various objects? Then geometry is the branch you must explore. Dealing with the shape, sizes, and volumes of figures, geometry is a practical branch of mathematics that focuses on the study of polygons, shapes, and geometric objects in both two-dimensions and three-dimensions. Congruence of objects is studied at the same time focussing on their special properties and calculation of their area, volume, and perimeter. The importance of geometry lies in its actual usage while creating objects in practical life.
The importance of geometry lies in its actual usage while creating objects in practical life.
Coordinate Geometry Formulas
Trigonometry
Derived from Greek words “trigonon” meaning triangle and “metron” meaning “measure”, trigonometry focuses on studying angles and sides of triangles to measure the distance and length. Amongst the prominent branches of mathematics used in the world of technology and science to develop objects, trigonometry is a study of the correlation between the angles and sides of the triangle. It is all about different triangles and their properties!
Trigonometry Formulas
Calculus
“Calculus is the most powerful weapon of thought yet devised by the wit of man.”
– Wallace B. Smith
It is one of the advanced branches of mathematics and studies the rate of change. With the advent of calculus, a revolutionary change was brought about in the study of maths. Earlier, maths could only work on static objects but with calculus, mathematical principles began to be applied to objects in motion. Used in a multitude of fields, the branch can be further categorized into the differential and integral calculus both starkly different from each other. A branch with mind-numbing questions, calculus is an interesting concept introduced to students at a later stage of their study in mathematics.
Earlier, maths could only work on static objects but with calculus, mathematical principles began to be applied to objects in motion. Used in a multitude of fields, the branch can be further categorized into the differential and integral calculus both starkly different from each other. A branch with mind-numbing questions, calculus is an interesting concept introduced to students at a later stage of their study in mathematics.
Fun Fact: “Forty” is the only number that is spelled with letters arranged in alphabetical order.
The abstract branch of mathematics, probability and statistics use mathematical concepts to predict events that are likely to happen and organize, analyze, and interpret a collection of data. Amongst the relatively newer branches of mathematics, it has become indispensable because of its use in both natural and social sciences. The scope of this branch involves studying the laws and principles governing numerical data and random events. Presenting an interesting study, statistics, and probability is a branch full of surprises.
Presenting an interesting study, statistics, and probability is a branch full of surprises.
Statistics Formulas for Competitive Exams
Number Theory
“Mathematics is the queen of the sciences, and number theory is the queen of mathematics.”
– Carl Friedrich Gauss
As the name suggests, Number theory is one of the oldest branches of Mathematics that established a relationship between numbers belonging to the set of real numbers. The basic level of Number Theory includes an introduction to properties of integers like addition, subtraction, multiplication, modulus and builds up to complex systems like cryptography, game theory and more.
Topology
“The basic ideas and simplest facts of set-theoretic topology are needed in the most diverse areas of mathematics; the concepts of topological and metric spaces, of compactness, the properties of continuous functions and the like are often indispensable. ”
”
– Pavel Sergeevich Aleksandrov
Topology is a much recent addition to the branches of Mathematics list. It is concerned with the deformations in different geometrical shapes under stretching, crumpling, twisting and bedding. Deformations like cutting and tearing are not included in topologies. Its application can be observed in differentiable equations, dynamical systems, knot theory, and Riemann surfaces in complex analysis.
Fun Fact: Every odd number has an “e” in it.
Advanced Branches of Mathematics
There are a vast number of advanced branches which are a part of the major branches mentioned above. These branches are studied at an advanced level and involve complex concepts that need strong computational skills. Such advanced branches are listed below.
Here are the 10 branches of mathematics:
- Matrix Algebra
- Numerical Analysis
- Operations Research
- Complex Numbers
- Calculus
- Set Theory
- Game Theory
- Analysis
- Cartesian Geometry
- Combinatorics
Applied Mathematics and Computation
Branches of Pure Mathematics
Pure mathematics can be simply described as the study of mathematical concepts purely based on maths and independent of any concept outside of mathematics.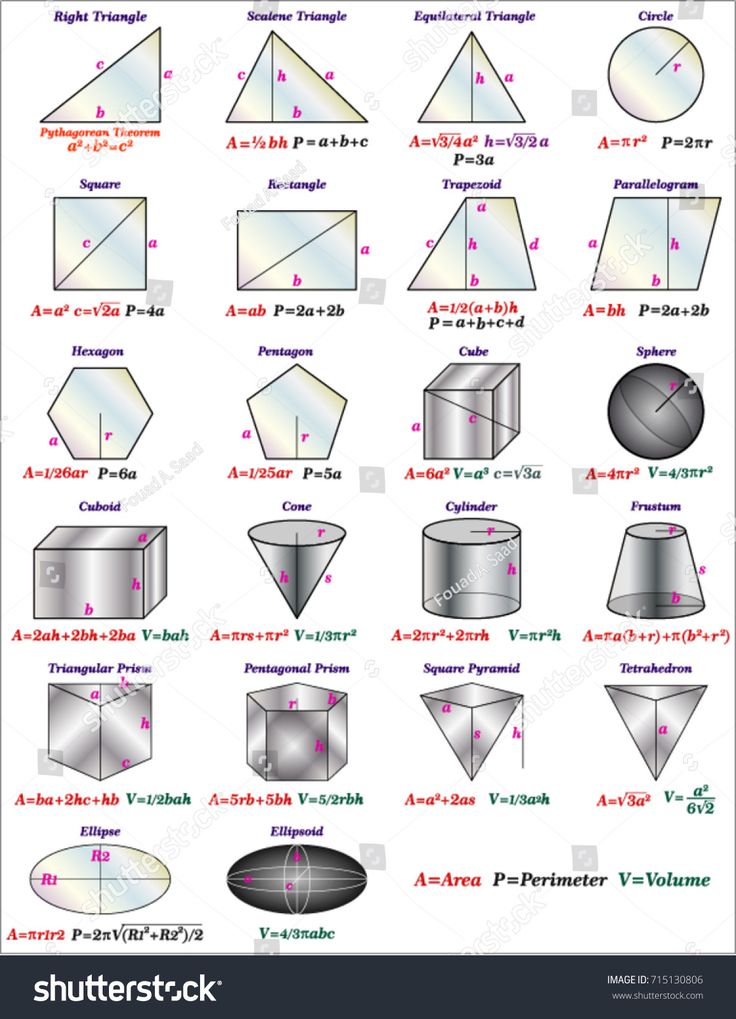 Here is the list of branches of Pure Mathematics:
Here is the list of branches of Pure Mathematics:
- Algebra
- Number Theory
- Geometry
- Arithmetic
- Topology
- Combinatorics
- Mathematical Analysis
Branches of Applied Mathematics
Applied Mathematics uses the applications of varied other disciplines and combines it with mathematical concepts. It is simply the combined application of mathematics with specialised knowledge.
Here are the branches of applied mathematics:
- Statistics and Probability
- Set Theory
- Calculus
- Trigonometry
Fun Fact: Archimedes [287 – 212 BC] is the father of Mathematics
Top Universities for Courses in Mathematics
For aspirants wishing to establish a career in mathematics, the first step is to pursue a course in your chosen branch of Mathematics. Many renowned universities of the world offer lauded degrees in mathematics and its varied branches. Being aware of the major picks available to one helps in reducing the dilemma that comes with choosing the university. Tabulated below are some of the top class universities offering esteemed mathematics programs.
Tabulated below are some of the top class universities offering esteemed mathematics programs.
Top Indian Colleges for Mathematics
- Fergusson College
- Mount Carmel College
- Stella Maris College
- St. Xavier’s College
- Jadavpur University
- St.Stephen’s College
- Ramakrishna Mission Vivekananda College
- Christ University
Career Options in Mathematics
If the number game attracts you and you can’t help but add or multiply any number you see, then you should pick up Mathematics as a career. You can become one of the following professionals if you choose a career in Mathematics:-
- Teacher/Lecturer– You can teach mathematics at the high school level and even university level if you are qualified enough and even explore research via postgraduation.
- Statistician- A statistician collects data, turns them into charts and graphs and makes interpretations which is an important aspect in all professions.
- Data Analyst/Scientist– A data analyst/scientist is similar to a statistician but with certain differences. In Data Science, you will use scientific methods of data collection, comparison and give solutions to the organisation relatively.
- Mathematician– A mathematician is involved in all fields of profession. Whether it be inventing new business valuation methods or creating a formula that sends a rocket to the ISS, a mathematician does it all.
- Cryptographer– A cryptographer is a person who encodes and decodes various symbols or modes of communication to decipher what it means. Additionally, they also create safe codes for the military or other organisations.
Every profession needs the Branches of Mathematics as the subject ties all the broken pieces and creates uniformity.
FAQs
What are the four branches of Mathematics?
Algebra, Geometry, Calculus and Statistics & Probability are considered to be the 4 main branches of Mathematics.
What is the hardest branch of Maths?
Algebra is the hardest branch of Maths. Abstract algebra particularly is the most difficult portion as it includes complex and infinite spaces.
Who is the father of Mathematics?
Archimedes [287 – 212 BC] is the father of Mathematics
Who invented Math?
It is difficult to trace back the exact origins of Maths. But it is estimated that in early 6th century, Pythagoreans invented Maths. After that Euclid introduced the axiomatic method consisting of the definition, axiom, theorem, and proof.
BSc Mathematics
MSc Mathematics
Are you intrigued by numbers and have a flair for doing difficult numeric calculations? Then, Mathematics is an all-encompassing science that deals with quantity, space and numbers and abstract concepts as well as applied maths in other fields. While at first glance it might be difficult to identify the branches of mathematics, it is imperative to possess knowledge about them for any student wishing to gain a holistic idea about the subject. We hope this blog has presented a comprehensive list of different areas of study and branches of mathematics. (Phentermine) Planning to study a degree in Mathematics? Experts at Leverage Edu can help you find the best course and university as well as assist you throughout the admission process to ensure that you send a winning application! Sign up for a free session today!
While at first glance it might be difficult to identify the branches of mathematics, it is imperative to possess knowledge about them for any student wishing to gain a holistic idea about the subject. We hope this blog has presented a comprehensive list of different areas of study and branches of mathematics. (Phentermine) Planning to study a degree in Mathematics? Experts at Leverage Edu can help you find the best course and university as well as assist you throughout the admission process to ensure that you send a winning application! Sign up for a free session today!
Shakuntala Devi rightly said that without mathematics, there is nothing you can do. To explore more, let’s first know the 5 main branches of mathematics, i.e. Algebra, Number Theory, Arithmetic and Geometry. In the past 2 decades or so, our modern world has introduced more branches like Probability and Statistics, Topology, Matrix Algebra, Game Theory, Operations Research derived from these oldest branches of math. Breaking the myth of mathematics being called boring, we bring to you all about branches of mathematics with their list, tree and career options!
Breaking the myth of mathematics being called boring, we bring to you all about branches of mathematics with their list, tree and career options!
Check Out: Vedic Maths
Tree of the Branches of Mathematics
Branches of MathematicsMain Branches of Mathematics
YouTube: DOS- Domain of ScienceMathematics is a complex area of study and comprises interlinked topics and overlapping concepts. Additionally, extensive analysis of the branches of mathematics helps students in organizing their concepts clearly and developing a strong foundation. Being aware of the differences and uniqueness of branches of mathematics helps in methodically studying various concepts of maths and also guides students in deciding the branch they would like to pursue as a career.
Here are the main branches of mathematics:
- Foundations
- Arithmetic
- Algebra
- Geometry
- Trigonometry
- Calculus
- Probability and Statistics
- Number Theory
- Topology
Below explained are the important branches of mathematics with their unique features and distinct concepts. These branches are important for laying a strong foundation for mathematics.
These branches are important for laying a strong foundation for mathematics.
Fun Fact: -40 °C is equal to -40 °F.
Arithmetic
“Arithmetic must be discovered in just the same sense in which Columbus discovered the West Indies, and we no more create numbers than he created the Indians.”
– Bertrand Russell
Arithmetic is one of the most basic branches of mathematics and deals with numbers and their applications in many ways. Addition, subtraction, multiplication, and division are used as the basic groundwork to solve a large number of questions and progress into more complex concepts like exponents, limits, and many other types of calculations. This is one of the most important branches because its fundamentals are used in everyday life for a variety of reasons from simple calculations to profit and loss computation.
Word Problems on Arithmetic Operations
Arithmetic Reasoning
Algebra
“The algebraic sum of all the transformations occurring in a cyclical process can only be positive, or, as an extreme case, equal to nothing. ”
”
– Rudolf Clausius
A broad field of mathematics, algebra deals with solving generic algebraic expressions and manipulating them to arrive at results. Unknown quantities denoted by alphabets that form a part of an equation are solved for and the value of the variable is determined. A fascinating branch of mathematics involves complicated solutions and formulas to derive answers to the problems posed.
Algebra Questions
Algebra Formulas
Fun Fact: The word “mathematics” only appears in one Shakespearean play, “The Taming of the Shrew”.
Geometry
“The description of right lines and circles, upon which geometry is founded, belongs to mechanics. Geometry does not teach us to draw these lines, but requires them to be drawn.”
-Isaac Newton
Do you often wonder about the shapes and sizes of various objects? Then geometry is the branch you must explore. Dealing with the shape, sizes, and volumes of figures, geometry is a practical branch of mathematics that focuses on the study of polygons, shapes, and geometric objects in both two-dimensions and three-dimensions. Congruence of objects is studied at the same time focussing on their special properties and calculation of their area, volume, and perimeter. The importance of geometry lies in its actual usage while creating objects in practical life.
Dealing with the shape, sizes, and volumes of figures, geometry is a practical branch of mathematics that focuses on the study of polygons, shapes, and geometric objects in both two-dimensions and three-dimensions. Congruence of objects is studied at the same time focussing on their special properties and calculation of their area, volume, and perimeter. The importance of geometry lies in its actual usage while creating objects in practical life.
Coordinate Geometry Formulas
Trigonometry
Derived from Greek words “trigonon” meaning triangle and “metron” meaning “measure”, trigonometry focuses on studying angles and sides of triangles to measure the distance and length. Amongst the prominent branches of mathematics used in the world of technology and science to develop objects, trigonometry is a study of the correlation between the angles and sides of the triangle. It is all about different triangles and their properties!
Trigonometry Formulas
Calculus
“Calculus is the most powerful weapon of thought yet devised by the wit of man. ”
”
– Wallace B. Smith
It is one of the advanced branches of mathematics and studies the rate of change. With the advent of calculus, a revolutionary change was brought about in the study of maths. Earlier, maths could only work on static objects but with calculus, mathematical principles began to be applied to objects in motion. Used in a multitude of fields, the branch can be further categorized into the differential and integral calculus both starkly different from each other. A branch with mind-numbing questions, calculus is an interesting concept introduced to students at a later stage of their study in mathematics.
Fun Fact: “Forty” is the only number that is spelled with letters arranged in alphabetical order.
The abstract branch of mathematics, probability and statistics use mathematical concepts to predict events that are likely to happen and organize, analyze, and interpret a collection of data. Amongst the relatively newer branches of mathematics, it has become indispensable because of its use in both natural and social sciences. The scope of this branch involves studying the laws and principles governing numerical data and random events. Presenting an interesting study, statistics, and probability is a branch full of surprises.
The scope of this branch involves studying the laws and principles governing numerical data and random events. Presenting an interesting study, statistics, and probability is a branch full of surprises.
Statistics Formulas for Competitive Exams
Number Theory
“Mathematics is the queen of the sciences, and number theory is the queen of mathematics.”
– Carl Friedrich Gauss
As the name suggests, Number theory is one of the oldest branches of Mathematics that established a relationship between numbers belonging to the set of real numbers. The basic level of Number Theory includes an introduction to properties of integers like addition, subtraction, multiplication, modulus and builds up to complex systems like cryptography, game theory and more.
Topology
“The basic ideas and simplest facts of set-theoretic topology are needed in the most diverse areas of mathematics; the concepts of topological and metric spaces, of compactness, the properties of continuous functions and the like are often indispensable. ”
”
– Pavel Sergeevich Aleksandrov
Topology is a much recent addition to the branches of Mathematics list. It is concerned with the deformations in different geometrical shapes under stretching, crumpling, twisting and bedding. Deformations like cutting and tearing are not included in topologies. Its application can be observed in differentiable equations, dynamical systems, knot theory, and Riemann surfaces in complex analysis.
Fun Fact: Every odd number has an “e” in it.
Advanced Branches of Mathematics
There are a vast number of advanced branches which are a part of the major branches mentioned above. These branches are studied at an advanced level and involve complex concepts that need strong computational skills. Such advanced branches are listed below.
Here are the 10 branches of mathematics:
- Matrix Algebra
- Numerical Analysis
- Operations Research
- Complex Numbers
- Calculus
- Set Theory
- Game Theory
- Analysis
- Cartesian Geometry
- Combinatorics
Applied Mathematics and Computation
Branches of Pure Mathematics
Pure mathematics can be simply described as the study of mathematical concepts purely based on maths and independent of any concept outside of mathematics. Here is the list of branches of Pure Mathematics:
Here is the list of branches of Pure Mathematics:
- Algebra
- Number Theory
- Geometry
- Arithmetic
- Topology
- Combinatorics
- Mathematical Analysis
Branches of Applied Mathematics
Applied Mathematics uses the applications of varied other disciplines and combines it with mathematical concepts. It is simply the combined application of mathematics with specialised knowledge.
Here are the branches of applied mathematics:
- Statistics and Probability
- Set Theory
- Calculus
- Trigonometry
Fun Fact: Archimedes [287 – 212 BC] is the father of Mathematics
Top Universities for Courses in Mathematics
For aspirants wishing to establish a career in mathematics, the first step is to pursue a course in your chosen branch of Mathematics. Many renowned universities of the world offer lauded degrees in mathematics and its varied branches. Being aware of the major picks available to one helps in reducing the dilemma that comes with choosing the university. Tabulated below are some of the top class universities offering esteemed mathematics programs.
Tabulated below are some of the top class universities offering esteemed mathematics programs.
Top Indian Colleges for Mathematics
- Fergusson College
- Mount Carmel College
- Stella Maris College
- St. Xavier’s College
- Jadavpur University
- St.Stephen’s College
- Ramakrishna Mission Vivekananda College
- Christ University
Career Options in Mathematics
If the number game attracts you and you can’t help but add or multiply any number you see, then you should pick up Mathematics as a career. You can become one of the following professionals if you choose a career in Mathematics:-
- Teacher/Lecturer– You can teach mathematics at the high school level and even university level if you are qualified enough and even explore research via postgraduation.
- Statistician- A statistician collects data, turns them into charts and graphs and makes interpretations which is an important aspect in all professions.

- Data Analyst/Scientist– A data analyst/scientist is similar to a statistician but with certain differences. In Data Science, you will use scientific methods of data collection, comparison and give solutions to the organisation relatively.
- Mathematician– A mathematician is involved in all fields of profession. Whether it be inventing new business valuation methods or creating a formula that sends a rocket to the ISS, a mathematician does it all.
- Cryptographer– A cryptographer is a person who encodes and decodes various symbols or modes of communication to decipher what it means. Additionally, they also create safe codes for the military or other organisations.
Every profession needs the Branches of Mathematics as the subject ties all the broken pieces and creates uniformity.
FAQs
What are the four branches of Mathematics?
Algebra, Geometry, Calculus and Statistics & Probability are considered to be the 4 main branches of Mathematics.
What is the hardest branch of Maths?
Algebra is the hardest branch of Maths. Abstract algebra particularly is the most difficult portion as it includes complex and infinite spaces.
Who is the father of Mathematics?
Archimedes [287 – 212 BC] is the father of Mathematics
Who invented Math?
It is difficult to trace back the exact origins of Maths. But it is estimated that in early 6th century, Pythagoreans invented Maths. After that Euclid introduced the axiomatic method consisting of the definition, axiom, theorem, and proof.
BSc Mathematics
MSc Mathematics
Are you intrigued by numbers and have a flair for doing difficult numeric calculations? Then, Mathematics is an all-encompassing science that deals with quantity, space and numbers and abstract concepts as well as applied maths in other fields. While at first glance it might be difficult to identify the branches of mathematics, it is imperative to possess knowledge about them for any student wishing to gain a holistic idea about the subject. We hope this blog has presented a comprehensive list of different areas of study and branches of mathematics. (Phentermine) Planning to study a degree in Mathematics? Experts at Leverage Edu can help you find the best course and university as well as assist you throughout the admission process to ensure that you send a winning application! Sign up for a free session today!
While at first glance it might be difficult to identify the branches of mathematics, it is imperative to possess knowledge about them for any student wishing to gain a holistic idea about the subject. We hope this blog has presented a comprehensive list of different areas of study and branches of mathematics. (Phentermine) Planning to study a degree in Mathematics? Experts at Leverage Edu can help you find the best course and university as well as assist you throughout the admission process to ensure that you send a winning application! Sign up for a free session today!
Dictionary of terms in mathematics from A to Z - POCHEMUKHA.RU answers to questions.
Axiom is a statement accepted without proof.
The algebraic expression is a number of numbers, denoted by letters or numbers, and connected using the operations of addition, subtraction, multiplication, division, raising to a power, and extracting a root.
Abcissa (French word). One of the Cartesian coordinate points. Is the first. It is usually denoted by the symbol "X". First used by G. Leibniz in 1675 (German scientist).
One of the Cartesian coordinate points. Is the first. It is usually denoted by the symbol "X". First used by G. Leibniz in 1675 (German scientist).
Additivity. Some property of quantities. He speaks about the following: the value of a certain quantity corresponding to a full-fledged object is equal to the sum of the values of such a quantity that correspond to its parts in any division of a full-fledged object into parts.
Adjunct. Fully corresponds to algebraic addition.
Axonometric. One of the ways to represent spatial figures on a plane.
Algebra. Part of mathematics that studies problems and solutions of algebraic equations. The term was first seen in the 11th century. Applied Muhammed ben-Musa al-Khwarizmi (mathematician and astronomer).
Argument (function). Variable value (independent) with which the value of the function is determined.
Arithmetic.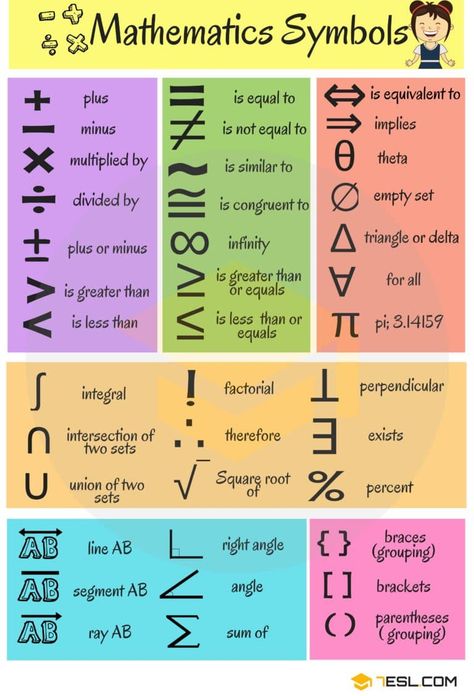 The science that studies operations on numbers. Originated in Babylon, India, China, Egypt.
The science that studies operations on numbers. Originated in Babylon, India, China, Egypt.
Asymmetric. Absence or violation of symmetry (inverse of symmetry).
Infinitely large value is greater than any given number.
An infinitely small value is less than any finite value.
Billion. One thousand million (one followed by nine zeros).
Bisector. A ray starting at the corner vertex (divides the corner into two parts).
Vector. Directed straight line segment. One end is the beginning of the vector; the other is the end of the vector. For the first time the term was used by W. Hamilton (an Irish scientist).
Vertical corners. A pair of corners that has a common vertex (formed by the intersection of two lines in such a way that the side of one corner is a direct continuation of the second).
Vector is a quantity characterized not only by its numerical value, but also by its direction.
Graph - a drawing that clearly depicts the dependence of one value on another, a line that gives a visual representation of the nature of the change in the function.
Hexahedron. Hexagon. The term was first used by Pappus of Alexandria (Ancient Greek scholar).
Geometry. Part of mathematics that studies spatial forms and relationships. The term was first used in Babylon/Egypt (5th century BC).
Hyperbole. Open curve (consists of two unrestricted branches). The term appeared thanks to Apollonius of Perm (ancient Greek scientist).
Hypocycloid. This is the curve that the point of the circle describes.
Homothety. An arrangement between figures (similar), in which the lines connecting the points of these figures intersect at the same point (this is called the center of the homothety).
Degree. Unit for flat corner. Equal to 1/90 of a right angle. Measuring angles in degrees began more than 3 centuries ago. For the first time such measurements were used in Babylon.
Deduction. Form of thinking. With its help, any statement is deduced logically (based on the rules of the modern science of "logic").
Diagonal. A line segment that connects the vertices of a triangle (they do not lie on the same side). First used the term Euclid (3rd century BC).
Discriminant. An expression made up of the values that define the function.
Fraction is a number made up of a whole number of fractions of one. It is expressed as the ratio of two integers m/n, where m is the numerator showing how many parts of the unit are in the fraction, and n is the denominator showing how many parts the unit is divided into.
Denominator. Numbers that make up a fraction.
The golden ratio is the division of a segment into two parts so that the larger part is related to the smaller one, as the entire segment is to the larger part. Approximately equal to 1.618. The criterion of beauty, used in architecture, etc. The term was introduced by Leonardo da Vinci.
Index. Alphabetic or numeric index. With its help, mathematical expressions are supplied (this is done in order to distinguish from each other).
Induction. Method for proving a mathematical equation.
Int. Basic concept of mathematical analysis. It arose due to the fact that it took to measure volumes and areas.
Irrational number. A number that is not rational.
Leg. One of the sides of a right triangle that is adjacent to a right angle.
Square Regular quadrilateral (or rhombus). Each corner of the square is a straight line. All angles in a square are equal (by 90 degrees).
All angles in a square are equal (by 90 degrees).
Mathematical constant. A value that never changes in its value. A constant is the opposite of a variable.
Cone. A body that is bounded by a single cavity by means of a conical surface. It intersects a plane (the plane is perpendicular to its axis).
Cosine. Is one of the trigonometric functions. The designation in mathematics/higher mathematics is cos.
Equation root - solution, the value of the unknown, found through known coefficients.
The constant is a constant value.
Coordinates are numbers that define the position of a point on a plane, surface, or in space.
Logarithm. Exponent "m". It must be raised to the "a" power in order to get some NT. For the first time, the logarithm was proposed by J. Napier.
Line is the common part of two adjacent surface areas.
Max. Highest value of the function.
Scale. The ratio of two linear dimensions to each other. Used in many modern industries. The main - cartography, geodesy.
Matrix. Rectangular table. It is formed using the set of a number (definite). Includes columns and rows (matrix structure). For the first time, the term "matrix" appeared with the scientist J. Sylvester.
Median. A segment that connects the vertex of a triangle and its midpoint on the opposite side.
Minimum. Smallest value of the function.
Polygon. Geometric figure. The definition is a closed broken line.
Module. Absolute value (real number).
The set is a collection of elements united by some attribute.
Norm. The absolute value of the number.
The inequality is two numbers or expressions connected by signs (greater than) or (less than).
Oval. Convex, closed figure (flat).
Circle. Numerous points located on a plane.
Ordinate. One of the Cartesian coordinates. It is usually designated as the second.
Octahedron. Geometric figure. One of the five polyhedra (regular). The octahedron includes 8 faces (regular), 6 vertices and 12 edges.
Parallelepiped. Prism. The base is a parallelogram or a polyhedron (equivalent concepts). Has 6 edges. Each face is a parallelogram.
Parallelogram. Quadrilateral. Its opposite sides are parallel (in pairs). At the moment, there are 2 special cases of a parallelogram: a rhombus and a square. The main property of this geometric figure:
• Opposite sides are equal;
• Opposite angles are equal.
Perimeter. The sum of all sides of a geometric figure. For the first time it was possible to meet at Archimedes and Heron (ancient Greek scientists).
Perpendicular. A straight line that intersects a plane (any) at a right angle.
Pyramid. Polyhedron. Its base is a polygon. Any other face is a triangle (these faces have a common vertex). At the moment, pyramids can be of various types: triangular, quadrangular, and so on (they are distinguished by determining the number of corners).
Planimetry. One of the most important parts of elementary (simple) geometry. Planimetry studies the properties of figures that are on a plane. For the first time, the term was designated by Eculid (an ancient Greek scientist).
Plus. A sign that denotes a mathematical operation - addition. In addition, positive numbers are denoted with a plus. For the first time, the sign was introduced by J. Vidman (a famous Czech scientist).
Limit. The basic concept of mathematics. Denotes: a variable value approaches a constant value (defined) indefinitely. The term was first used by the famous scientist Newton.
The term was first used by the famous scientist Newton.
Prism. Polyhedron. The first 2 faces are equal angles (these are the bases of the prism). The rest is the side faces.
Projection. One of the ways to depict spatial and flat figures.
Variable is a value whose numerical value changes according to a certain, known or unknown law.
Plane is the simplest surface. Any line connecting two of its points belongs entirely to it.
Line is a set of points common to two intersecting planes.
Percentage is a hundredth of a number.
Radian. Angle unit.
Rhombus. Parallelogram. All sides of this figure are equal. A rhombus having right angles has the term "square".
Segment. Part of a circle (limited by a chord that connects the ends of the arc).
Secant. Trigonometric function. The designation in mathematics/higher mathematics is sec.
Sector. Part of a circle. Constrained by a circle + two radii (connects the ends of one arc to the center of the circle).
Symmetry - match.
Sinus. Trigonometric function. The designation in mathematics / higher mathematics is sin.
Stereometry. Part of elementary geometry. Engaged in the study of full-fledged spatial figures.
Tangent. Trigonometric function. The designation in mathematics/higher mathematics is tg.
Tetrahedron. Polyhedron, includes 4 triangular faces. Each vertex has 3 faces (converge at the vertices). A tetrahedron has 4 faces + 6 edges + 4 vertices.
Dot. Has no definite and final concept. Any point is denoted by letters A, B, C.
Triangle. Polygon (simple). Includes 3 tops + 3 sides;
Includes 3 tops + 3 sides;
Theorem is a statement to be proved based on axioms and previously proven theorems.
Identity is an equality valid for all values of the coefficients included in it.
Topology is a branch of mathematics that studies the properties of figures that do not change under any deformations carried out without ruptures and gluing.
An equation is a mathematical notation of the problem of finding the values of unknowns under which the values of two given functions are equal.
Angle. Geometric figure (flat). It is formed by two rays that come out of one point (the points are the corner vertices).
Factorial is the product of natural numbers from 1 to any given natural number n. Denoted n!. Factorial of zero o! = 1.
The formula is a combination of mathematical symbols that expresses a sentence.
Function is a numerical relationship between elements of two sets, in which one element of one set corresponds to a certain element of another set. Can be given by formula or graph.
Can be given by formula or graph.
Chord. A segment that connects 2 points on a circle.
Digits are symbols for numbers.
Central The middle of something (for example: a circle).
Cyl. A body bounded by a cylindrical surface + parallel planes (two). For the first time, the concept of "cylinder" could be found in Euclid and Aristarchus.
Compass. Special instrument designed for drawing arcs, linear measurements and circles.
Numerator. A specific number with which a fraction is composed. The term was first used by Maxim Planuda (Byzantine scholar).
The number is one of the basic concepts of mathematics that arose in connection with the counting of individual objects.
Ball. Geometric body. It is the total set of all points in a certain space.
Exhibitor. Same as exponential function. The term was first introduced by G. Leibniz (a German scientist).
The term was first introduced by G. Leibniz (a German scientist).
Ellipse. Oval curve. For the first time this term was introduced by Apollonius of Perga (an ancient Greek scientist).
Dictionary of mathematical terms for elementary school
Algorithm - specific sequence of operations or calculations.
More than (>)-in combined with quantitative names denotes an excess of the specified quantity.
Letter expression - entries in which numbers and letters are connected by action signs.
Century - a period of time of one hundred years.
The expression - is a record, composed of numbers, brackets and arithmetic signs
Subtraction - the inverse of addition is an arithmetic operation by means of which from one value another value is subtracted.
Subtracted - value (number) that is subtracted from another value (number).
A hectare is a unit of land area equal to 10,000 square meters.
Year - is unit of chronology, a period of time equal to the period of revolution of the Earth around the Sun and containing twelve calendar months, deducted from 1 January, as well as the digital designation of such an interval.
Gram - Unit mass in metric units, one thousandth of a kilogram.
Division - inverse multiplication mathematical operation - finding one of the factors by the product and the other factor.
Dividend - the number or value to be divided.
Divisor - the number or amount by which the dividend is divided.
Divide - perform the action of division on any number.
Decimeter - a unit of length equal to one tenth of a meter.
Diagonal - a straight line segment connecting two vertices
polygons not lying on the same side, or two vertices of the
polyhedron that do not lie on one edge.
Diagram - a graphic image that clearly shows
the relationship between any values.
Diameter - straight line segment connecting two points circles
and passing through its center, as well as the length this segment.
Length - size, length, distance between the ends of something.
Share - a part that, together with other similar or similar parts, constitutes a whole.
Unit - real number, from multiplication by which any number does not change, as well as a figure depicting this number.
Problem - a question (usually of a mathematical nature) that requires finding a solution using known data subject to certain conditions.
A square is a rectangle with equal sides.
Kilometer is a unit of length equal to 1000 meters.
Circle - an object in the form of a circle, part of a plane, bounded by a circle.
Cone - geometric body formed by the rotation of a rectangular triangle around one of its legs.
A cube is a regular polyhedron with six faces.

Line - dash on plane, on some surface or in space.
Liter is a unit of volume and capacity equal to 1000 cubic meters. see, a also the amount of liquid of that volume.
Broken line - line consisting of straight line segments connected at an angle.
Beam - one of the straight lines diverging in different directions from one centre.
Mass - quantity, volume of something.
Mathematics - science, studying quantities, quantitative relations and spatial forms.
Less than (<)-v in combination with quantitative names means a decrease in the specified quantity.
Meter - basic unit of length in the International System of Units, equal to 100 cm
Millimeter - a unit of length equal to one thousandth of a meter.
Minus sign in dash (-), denoting subtraction or a negative value in mathematics
Minute - unit time, equal to 1/60 of an hour and consisting of 60 seconds; such a period of time length.

Multi-digit something there are "many signs" consisting of many digital
characters.
Polygon - geometric figure, bounded by a closed
broken line, the links of which form more than four corners.
Multiplier - second of two multiplied numbers or quantities.
Inequality - ratio between quantities showing that one quantity more or less than the other. Inequality sign (>, <).
Zero - digit "0", denoting such a number, a real number whose addition does not change any number.
Oval - a figure bounded by an egg-shaped curved line.
Circle - a curve closed on a plane, all points of which are equal removed from the center.
Acute angle - angle less than 90 degrees.
Segment - part of a straight line lying between two of its points.
Palette - a transparent plate with a grid of squares applied to it, used to calculate areas on plans and maps.
Perimeter - the sum of the lengths of all sides of a geometric figure.
Pyramid - a polyhedron whose base is
a polygon, and the side faces are triangles having a common vertex
Area - the value of something in length and width, measured in square units
Plus - plus sign (+) indicating addition or a positive value.
Example - math exercise, requiring some operations on numbers.
The product of is the result, the result of multiplication.
Straight - straight line.
Right angle - 90 degree angle.
Rectangle - a quadrilateral with all right angles.
Equals - sign equals (=), the same.
Radius is a segment connecting the center of the circle with any of its points, as well as the length this segment.
Equality - a relation between quantities showing that one quantity is equal to another.
Difference - the number that makes up the remainder when subtracted.
Distance - the space separating two points, the gap between anything.
Rhombus - parallelogram, all sides of which are equal.
Ruble is the main monetary unit, equal to 100 kopecks, as well as a banknote and a coin of this value.
Centimeter is a unit of length, a hundredth of a meter.
Second - 1/60 fraction of a minute, the basic unit of time in the International System of Units.
Term - a number or expression that is added to another.
Addition - mathematical operation by which of two or several numbers (or values) get a new one containing as many units (or quantities), how many were in all given numbers (values) together.
Ton - unit of mass equal to 1000 kg. The amount of substance having that weight.
Point - graphic symbol as conventional designation for something.
 A place that has no dimension, the boundary of a line segment.
A place that has no dimension, the boundary of a line segment. Triangle - a geometric figure - a polygon with three corners.
Angle - geometric figure, formed by two straight lines emanating from one point
Multiplication - mathematical operation by which two numbers (or magnitudes) a new number (or magnitude) is obtained, which (for integers numbers) contains the summand of the first number as many times as there are units in the second.
Reduced - the name of the number from which another is subtracted.
Equation - mathematical equation with one or more unknown quantities (numbers or functions) that is true only for certain sets of these quantities.
Price - monetary value goods, fee.
centner - a measure of mass equal to 100 kg.
Digit - sign, denoting a number.
Hour is a period of time equal to sixty minutes, one twenty-fourth of a day.
Private - number obtained by dividing one value by another, result, result of division.