Math projects for first graders

First Grade Math Games That Will Really Engage Your Students

Early elementary teachers have a chance to instill in their students a love of math right from the start. One great way to do that is to make math fun! These first grade math games cover all the standard skills firsties need to know, in ways that make learning engaging and enjoyable for all.

(Just a heads up, WeAreTeachers may collect a share of sales from the links on this page. We only recommend items our team loves!)

1. Assemble a domino puzzle

Print the free puzzles at the link below. Then grab some dominoes and start filling in the puzzle one piece at a time by placing a domino that adds up to the number shown in each rectangle. The trick is that regular domino rules still apply, so each number must touch another domino with the same number on that end.

Learn more: Games 4 Gains

2. Play tic-tac-toe with addition problems

Work out the answer to each problem in the grid, and dot or circle the ones that add up to 10. First to get three in a row wins!

Learn more: 123Homeschool4Me—Tic-Tac-Toe Math Game

3. Face off in Dice War

Dice games are fantastic in the classroom! With this one, kids practice their addition facts and get a little work with subitizing too. The concept is so simple: Each player rolls the dice and adds up their numbers. The highest sum wins that round. This is one of those first grade math games that can be expanded by adding a third die. (You can also use playing cards.)

Learn more: Miss Giraffe’s Class

4. Use sticky notes to make 10

Sticky notes have so many uses in the classroom. In this case, challenge students to put together the numbered notes that “make 10.” They’ll practice adding to 10 with multiple numbers. You can also do this with subtraction, starting at 10, to make zero.

Learn more: Life Over C’s

5. Play Shut the Box

This game has been played for hundreds of years, but it’s a fun and sneaky way to practice addition facts fluency. The goal is to “close” each of the numbers in the box from one to nine by rolling the dice. For instance, if a player rolls 11, they may close 1, 2, 3, and 5, as these add up to 11. If no numbers are available to add up to the dice total, play passes to the next player and continues until someone finally “shuts the box” by closing the last available number. You can play this game with a specially designed box, as it has been played for years. You don’t need the box, though; simply have kids write out the numbers 1 through 9 and cross them out as they play.

6. Assemble some addition grab bags

Fill a variety of bags with collections of small objects. Kids grab a handful from two different bags, then count and add up the results. Be sure they write it all down to get practice at setting up equations. First grade math games like this one work for subtraction too.

Learn more: Susan Jones Teaching—Grab Bags

7. Face Off to find the difference

Each player rolls the dice (try polyhedral dice for higher numbers, or roll several dice and add them together) and builds a stack of math cubes. Then they “face off” and find the difference between their two stacks.

Learn more: Frugal Fun for Boys and Girls

8. Plant flowers and count on

Pick up some artificial flowers at the dollar store for this springtime garden game. Roll the die and add that number of flowers to your pot. Then roll again and add more, counting on from where you left off. Easy and fun!

Learn more: Fun-a-Day

9. Build and count on

Here’s a fun hands-on way to practice counting on and addition. You can use any type of building blocks for this one. Get free printables at the link.

Learn more: Susan Jones Teaching—Building On

10. Print a hundreds chart to play Battleship

Help students master numbers up to 100 by playing Battleship, using a standard hundreds chart. They’ll enjoy the strategy (and the fun of crying “boom!” when they sink a ship) while they develop number sense and practice number words.

Learn more: 123Homeschool4Me—Hundreds Chart Battleship

11.

These hundreds chart puzzles encourage kids to use a variety of first grade math skills to fill in the missing numbers. They’ll practice counting on, numbers to 100, skip counting, and more. Grab these 10 free printable puzzles at the link.

Learn more: Helping With Math

12. Try nuts and bolts for place-value practice

Mastering the concepts of tens and ones is more fun with hands-on activities. We love these DIY math manipulatives that use inexpensive nuts and bolts from the hardware store to drive home the idea of place value. (Bonus: Kids also practice fine motor skills!) Get free printable mats to use with this activity at the link.

Learn more: The Measured Mom

13. Have a place-value scavenger hunt

Grab a stack of old magazines and use it for a place-value scavenger hunt! You can do this one at school or send it home for homework. Get free printables to use for this first grade math game at the link.

Learn more: Primary Theme Park—Place Value Scavenger Hunt

14. Practice tens and ones with I Have, Who Has

As first graders work with the concepts of tens and ones, play this simple game to give them confidence. Using the free printable cards at the link, the first player calls out “I have …” followed by the number shown on their card in blocks. Then they call out the number on the bottom, and the player who has that number takes over.

Learn more: Playdough to Plato—I Have, Who Has

15. Deal Uno cards to compare numbers

Some first grade math games are just slightly harder versions of kindergarten ones. Make a greater than/less than mat with paper scraps and a brad, as shown. Lay out two Uno cards on each side, since first graders work on comparing two-digit numbers. Swing the arms of the signs around to the correct direction to indicate which is greater.

Learn more: The Kindergarten Smorgasboard

16. Knock down the pins with dot arrangement bowling

Take an inexpensive toy bowling set (or make your own with plastic bottles) and add sticky dots arranged in patterns. Students roll the ball and then have to quickly subitize to determine how many dots are on each pin they knocked down. If they get it right, they get the points!

Learn more: The First Grade Parade

17. Navigate a time-telling maze

Start with the first clock and color in the line that shows the correct time. That leads you to the next clock, and so on, until you’re done!

Learn more: 123Homeschool4Me—Time-Telling Maze

18. Assemble time-telling puzzles

Firsties should be mastering time to the hour and half hour. These free printable puzzles help them match up analog and digital clock times. Have them say the times out loud as they match them up too.

Learn more: 123Homeschool4Me—Time-Telling Puzzles

19. Match up plastic eggs

This is always a popular way to practice telling time. Draw clocks on one half of the eggs, and write out the times in numbers or words on the other half. For even more fun, hide the halves around the room and go on an egg hunt before you match them up!

Learn more: The STEM Laboratory

20.

Use pattern blocks with the free printable cards at the link to get kids playing around with simple geometry. They’ll practice recognizing basic shapes and learn they can use some shapes to make new ones.

Learn more: Susan Jones Teaching—Pattern Blocks

21. Partition and sort shapes

Gather up sticky notes in a variety of shapes and sizes. Draw lines on them to partition them equally or unequally. Then, have kids sort them based on type.

Learn more: Smitten With First

22. Build and measure with LEGO bricks

Everything is more fun with LEGO! Pull out a pile of square bricks and use them for these fun and free activities that incorporate estimating, measuring, and comparing length.

Learn more: Playdough to Plato—LEGO Math

23. Race and measure with toy cars

First, kids get a little STEM practice by figuring out how to build a ramp. Then, they race toy cars down the ramp, marking where they land. Finally, they compare distances using any kind of non-standard measurement they like.

Learn more: Susan Jones Teaching—Non-Standard Measurement

24. Sort out your classroom toys

First graders work on sorting by attribute in as many as three categories. Put out a variety of building blocks, beads, or other classroom toys and lay out some Hula-Hoops. Ask kids to define the categories and start sorting! You can even overlap the hoops into Venn diagrams for items that meet more than one criteria.

Learn more: BSM Year 2

25. Go on a bug hunt

Grab the free printable game at the link, then have kids graph their insects as they play. When they’re done, ask questions to ensure they understand the data they’ve collected.

Learn more: Primary Theme Park—Bug Hunt

Like these first grade math games? Don’t miss these 50 First Grade Math Word Problems of the Day!

Teachers deserve a strong support system. Find yours on the WeAreTeachers HELPLINE group on Facebook.

7 Common Core Math Activities for 1st Graders

For many teachers and administrators, the start of the 2013-14 school year also means the full implementation of the Common Core State Standards. Because the CCSS are guidelines and not a national curriculum, many first grade teachers looking to meet new Grade 1 math standards for their kiddoes have been busily preparing new lesson plans over the summer. Here are seven unique ideas for fun first grade CCSS-aligned math activities to get you started:

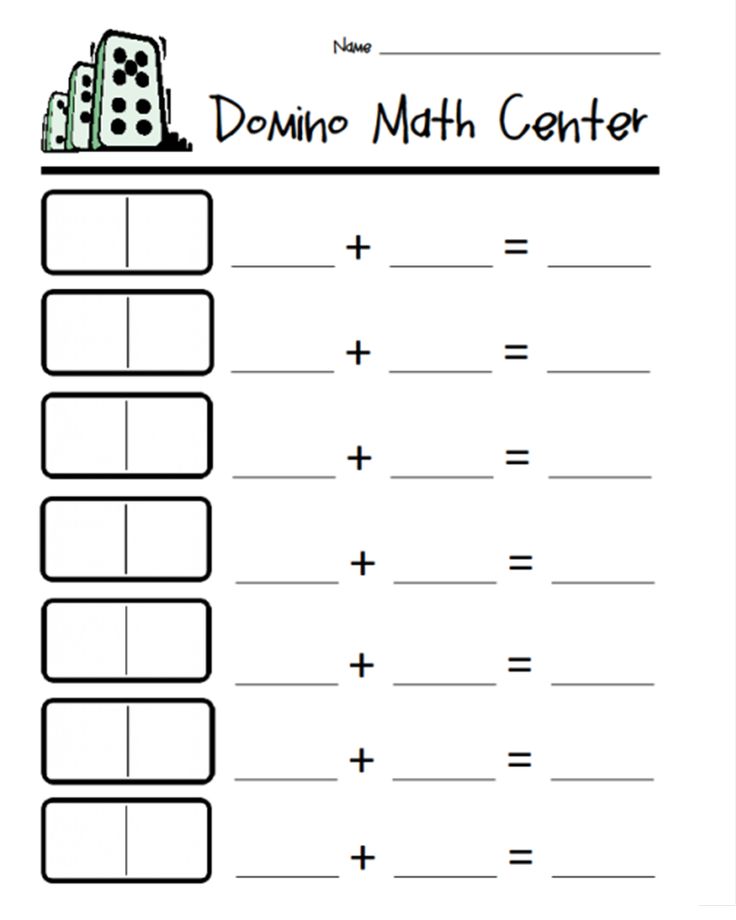
1. Dominoes

The CCSS require first graders to know how to represent and solve problems involving addition and subtraction. To make the process a little more fun, use dominoes to practice addition. Place a stack of numeral cards in front of the students and flip one over. Ask them to find dominoes that have that total number of dots, then have them record their thought processes on a sheet of paper as an addition equation.

2. Build trains with snap cubes

Snap cubes are one manipulative that presents endless possibilities for teaching first grade math. Under the CCSS, first graders need to understand that 5 + 3 = 3 + 5. Have students use snap cubes to create a train made of two colors (they can choose their favorite hues). Have them build a train using less than 10 cubes and write a number sentence describing what they’ve created. Then, have students flip the train and write the new sequence. This will help them understand that no matter the order of the numbers, the total is the same.

3. Bracelets

Bringing arts and crafts into math lessons always makes them more fun. To teach first graders about place value (for example, how a bundle of 10 can be thought of as 10 ones), create bracelets using pipe cleaner and beads. Have students each count out 10 beads of their favorite color and string them onto the pipe cleaner. After they’ve made the bracelets, show them how to push the beads to either side to demonstrate different pairs of numbers that can add up to 10.

4. Apple orchard field trip

It’s always fun to take math learning outside of the classroom, so why not take first graders on a field trip to the apple orchard? Have them count the apples as they each fill their own barrel. You can then use the different colored apples to demonstrate a word problem. For example, showing all of the different combinations of red and yellow apples that can be used to create a box of 10.

5. 100 day celebration

Reaching the 100th day of school is always exciting for students, so why not harness all of that energy into a math lesson? It’s great practice to support Common Core State Standards, which require first graders to be able to count to 120.  Have each student bring in a group of 100 items to celebrate and have a gallery walk around the classroom.

6. Plus one/minus one game

Why not create math activities using dice? To help first graders practice their addition and subtraction skills, create a mat resembling a bingo board that contains the numbers two through seven. Split students into pairs and give them each 10 counters (these can be anything from shapes made of construction paper to checkerboard pieces). Each player then takes a turn rolling the die and adding one (or subtracting one, depending on the game) and placing his or her counter on the corresponding number. The game ends when the students have used up all of their counters.

7. Fun DreamBox lessons

Kids today are tech savvy – most don’t remember a world without computers. To keep them engaged, use DreamBox Learning’s Intelligent Adaptive Learning technology to explore new concepts and build comprehension. The game-like learning environment, with lessons aligned to the Common Core, make learning fun with themes, characters, and a reward system.

Want more tips for successfully planning for CCSS math? Check out this free white paper from DreamBox.

Topics of research papers in mathematics

Attention! To repeat and consolidate the multiplication table and division table, we offer our game programs Multiplication table in cartoons and Division table in cartoons.

This page provides a general list of topics of research papers in mathematics for grades 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11, which can be accessed by clicking on the links and then on the pages you can select the topic of the project most appropriate to the level of knowledge and skills of the child. The project activity of the student begins only after the topic of the research work is approved by the supervisor (teacher).

The various topics of mathematics projects on this page can be taken as a basis, supplemented and changed in accordance with the goals of the study and the idea of ​​the project.

• Topics for projects in mathematics for grades 1, 2, 3, 4
• Topics for projects in mathematics for grade 5
• Topics for projects in mathematics for grade 6
• Topics for projects in mathematics for grade 7
• Topics for projects in mathematics for grade 8
• Topics for projects in mathematics for grade 9
• Topics for projects in mathematics for grade 10
• Topics for projects in mathematics for grade 11

Properly chosen topics for projects in mathematics for students in grades 5, 6, 7, 8, 9, 10 or 11 contribute to the fact that work on them will be really exciting, informative and interesting. Especially if this research project in mathematics is carried out by a group of children.

• Research topics in the history of mathematics
• Algebra Research Topics
• Logic research topics
• Geometry research topics
• Research papers on stereometry
• Research topics in combinatorics
• Research topics for mathematical games
• Topics of research papers in mathematics in subjects

The following topics for research papers and projects in mathematics are approximate, some of them can be combined into one topic if there are common tasks and goals of the study.

Topics for research projects in mathematics

Topics for design work in mathematics:

Author's tasks.
Aliquot fractions
Arithmetic of remainders. Modulo comparisons.
Without measuring stick
Without measuring stick, or measure with bare hands.
Endless world of numbers.
Divine number
Letter in a cube.
Quick account - easy and simple!
Quick calculation without a calculator.
In the depths of centuries, or As the ancients believed.
In the world of time (collection of creative tasks).
In the world of puzzles and labyrinths.
In the world of amazing numbers.
In search of optimal solutions.
In the realm of giant numbers.
Omnipresent mathematics.
Great tasks
Magnificent seven
Magnificent numbers.
Types of tasks for logical thinking.
Types and properties of movements.
Types of word problems and their solution.
Influence of the speed of falling raindrops on the speed of human movement during rain.
Harmony of law reigns in everything...
Time and its measurement
Time cannot be stopped, but can it be measured?
Time to work and time to rest.
Everything is a number
Everything about the "three" and a little more. ..
Everything about the number 13
Everything about the number 7
Is it always 2 x 2 = 4?
Calculation of the speed of the river.
Gallery of wonderful numbers.
Gallery of numerical curiosities.
Harmony and mathematics
Genetic code and Pythagorean square.
Geography of numbers
Hypothesis about the origins of the golden section.
Match Puzzle
Graphic methods and geometric considerations in solving problems in mathematics Graphic techniques in solving problems in mathematics.
Graphical method for solving plot problems.
Graphical way to multiply numbers.
Two ways to solve logical problems
Actions on numbers in different number systems.
Zero's birthday
Pi's birthday
Children's tasks for adult children.
Old Russian problems
Ancient number systems.
Ancient but eternally young prime numbers
Friendly triplets of numbers.
Friendly numbers
Heat of cold numbers
Living mathematics
Living nature and symmetry.
Paper strip mystery.
Riddle of Ramanujan
Riddles of the number series
Mysterious world of numbers.
Tasks from an old textbook.
Problems from Ethiopia
Problems for all occasions
Problems for the movement of two objects.
Problems on the movement along the river
Problems on checkered paper. Peak formula.
Problems based on local material
Tasks for the largest and smallest values ​​of quantities and methods for their solution.
Problems for optimization
Problems for liquid transfusion.
Cutting tasks
Outdoor tasks.
Problems for parity
Problems about labyrinths
Problems about four colors.

Topics for research projects in mathematics

Topics for research projects in mathematics:

Tasks of increased difficulty "on the move".
Tasks with restrictions.
Problems with the same numbers.
Problems with parameters
Problems with matches
Old and old problems.
Problems that could become theorems.
Wonderful numbers. Friendly numbers and twin primes.
Entertaining logic in mathematics
Entertaining problems
Entertaining problems of the distant past.
Entertaining problems in mathematics.
Entertaining numbers
Zanimatika
Entertaining flocks of prime numbers.
The origin and evolution of a mathematical problem.
Why does a person need measurements at different times?
Familiar and unfamiliar magic number Pi.
Acquaintance with symmetry
Measuring time.
Isoperimetric problem, or Dido's problem.
Exploring the possibility of using drawing in mathematics lessons.
Interesting and fast ways and methods of calculations.
Interesting and intellectual puzzles.
The art of guessing numbers
Use of mathematical cutting games.
The use of some provisions of number theory for solving problems of increased difficulty.
The use of ancient measures of length and weight for solving and compiling problems.
Study of mathematical abilities.
Study of the method of solving problems in various ways.
Study of a series of natural numbers.
Calculating time
How big is a million?
How to measure time?
How to measure the distance between relatives.
How to find a solution to the problem
How to cut a pie?
How to count without a computer and a calculator.
Calendars of time
Calendar distance of centuries
Calculators.
Square wheel - truth or myth?
Contact numbers and the thirteen ball problem.
Piggy bank of non-standard tasks in mathematics.
The Queen of Mathematics
Beautiful and fast ways of computing
Beauty in symmetry
Beauty and mathematics
Beauty through the prism of science
Cryptograms - cryptography of the past, present and future
Cryptography
Cryptography and cryptanalysis.
Cryptography and mathematics
Cryptography and steganography.
Cryptography as a method of encoding and decoding information.
Cryptography, mathematical algorithms for encryption.
Cryptography. The basics of encryption and the history of development.
Cryptography. Methods of its practical application.
Cryptography. Science of ciphers
Crystallography and mathematics
Winged mathematical expressions.
Curiosities, sophisms, paradoxes in mathematics.
Deft compasses
Magic secrets of the number 7
Magic numbers
Magic numbers in nature

Magic numbers and figures
Magic number "Pi"
Magic number of Scheherazade.
The magic of numbers
The magic of numbers 3, 11, 13
Mathematics in life: calculation of the repair work of the premises.
Mathematics in my future profession.
Mathematics around us
Mathematics on the chessboard.
Prodigy mathematicians
Mathematical processing of experimental data.
Mathematical formula of beauty.
Math Gems
Math Presentations
Mathematical sophisms.
Mathematical terms.
Mathematical billiards.
Mathematical calendar for schoolchildren.
Mathematical pendulum
Mathematical assistant
Mathematical modeling of the global development of mankind.
Mathematical modeling and its practical application.
Mathematical modeling as a way to solve problems (problems).
Mathematical modeling of the environment.
Mathematical modeling.
Mathematical description of random phenomena.
Mathematical journey into the world of harmony.
Materials for mathematical leisure.
The world of numbers, sounds and colors
Modeling of composite tasks.
The world of big numbers.
Modeling of text tasks.
Visual topology
Unknown about the known, or How to make a discovery. Is pi equal to 4?
Some interesting dependencies.
Unusual in ordinary numbers
Non-standard problems
Non-standard problems at Olympiads in Mathematics.
Zero has a special place in mathematics.
Numbering and number systems.
Numerology
Numerology - the magic of numbers
Numerology - myth or reality?
Numerology is the science of numbers in our life.
Numerology - modern science
Numerology in human life
Numerology: science or delusion?
In one stroke
Description of beauty and harmony of nature by mathematical relation.
Definition in the course of mathematics
Optical illusions and their application
Ornament as an imprint of the soul of the people.
Ornamental and geometric art by M. Escher.
Ornaments
From fingers to calculator
Discovery: coincidence or regularity?
The charm of prime numbers.
Palindromes in mathematics
Parameter. Dynamic illustrations for problem solving.
Letter with a secret
Planet of numbers
Through the pages of ageless Russian textbooks on mathematics.
Practical advice of mathematicians.
Traditions of antiquity far away (solution of ancient problems)
Devices, tools and devices for calculations.
Applied problems
Application of graphical methods in solving text problems.
The use of satellite images in the lesson of mathematics.
Pi calculation check.
Even parity check
Prime numbers
Contradiction of a consistent statement.
Journey to the origins of geometry.
Development of the concept of "infinity" in mathematics.
Talk about zero
Different ways of solving word problems.
The real world of imaginary numbers.

Recurrent relations and their application.
Solving diophantine equations
Solving problems by estimation method
Solving problems on mixtures and alloys.
Solving problems for compliance and exclusion of incorrect answers.
Solving problems according to ready-made drawings.
Solving problems on the topic "Movement along the river".
Solving optimization problems in mathematics.
Solving ancient problems
Solving text problems
Solving equations in integers.
The most interesting number
The secret of successful problem solving.
The seven greatest mysteries of mathematics.
Serious and funny in numbers
Symmetric prime numbers.
Number systems
Hidden modules
Perfect numbers
Perfect numbers. friendly numbers.
Perfect numbers. Mersenne prime numbers.
Reduced division using Horner's circuit.
Tasks will help you to save your health
Ways and techniques of quick calculations.
Ways of representing numbers in different number systems.
Methods for solving problems on the movement of bodies
Methods for the oral squaring of numbers.
Comparative analysis of the stability of some well-known ciphers.
Ancient problems
Ancient problems of ancient peoples.
Ancient entertaining tasks
Counting without a calculator
The mystery of even numbers
The mystery of the number "Pi"
Text problems in the school mathematics course.
Text problems and modeling.
Text problems for movement
Text problems for mixtures, alloys and solutions.
Text tasks for collaboration.
Mathematics textbook: yesterday, today, tomorrow
Figured numbers
Philosophical mystery of numbers
Philosophical aspects of mathematics
Finno-Ugric number system among other systems.
Folklore problems
Whole numbers and temperature measurement.
The price of one minute
Continued fractions
Number "9" in Tuvan numerology.
Digital roots
Numbers in our life.
Numbers around us
Pythagorean numbers and the beauty of the world.
Numbers rule the world
Numbers rule the world. Is it possible to imagine a world without numbers?
Numbers with proper names.
Number P.
A number that is larger than the Universe.
Numerical inequalities
The sixth mathematical action.
Six mathematical operations.
Ciphers and cryptograms.
Ciphers and mathematics
These amazing quaternions.

Jump to sections:
Research papers in mathematics
Research methods

If you want to place a link to this page, set one of the following codes on your site or forum:

Link code to the page with topics of mathematics projects:
Mathematics research topics links to the forum with topics of research papers in mathematics:
[URL=http://obuchonok.ru/node/431]Themes of research papers in mathematics[/URL]

If you like the page, share it on social networks:

Mathematics