Maths practice for kids

Logic Games | Fun Games for Kids

Kindergarten

1st Grade

2nd Grade

3rd Grade

4th Grade

5th Grade

6th Grade

Fun Games for Kids

Logic Games and Puzzles

New Blog: A Tale of Two Playgrounds

Category Spotlight: Skill Games

Featured Games

Code Panda

Red Block Returns

Zero Squares

Cookie Trail

Liquid Bubble Sort

Drop It

Find the Differences

Zero Numbers

Find the Pug

Globehopper

Monkey Bubbles

Happy Cups

NEW! Fun Logic Games at Puzzle Playground

Sokogem

Snake Falls

Reach the Flag

Kitty Gram

Sokonumber

Get the Stars

Give Your Brain a Workout

Mazes and Keys

Robot Islands PLUS

Color Maze

Drop the Number

Wind and Solar

One Liner

Jelly Doods

Dots and Boxes

Arty Agent

Paint the House Blue

Rescue Yellow

Chef Slash

Connect the Roads

Block the Pig

Logic Steps

Lightybulb 3

Car Park Puzzle

Cross the Bridge

Puzzle Ball

Double Up

Sudoku

Logic Tail

Robot Islands

The Parking Lot

Four Colors

Logic Magnets

Feed That Thing

3D Memory

Number Snake

Laser Trap

Trap the Mouse

Hex Blocks

Monsterland 4

Lightybulb

2048

Gnomy Night

Sorting Spheres

Andy's Golf

Red Block Returns

Islands Of Creatures

Maze Collapse

Gems Glow

Tic Tac Toe

Chess

Ghostie Loners

Animalines

Pin Cracker

Lightybulb 2

Scratch and Sniff

Fox Adventurer

Purple Mole

Brain Workouts

Monsterland 5

Green Mission

Reverse the Discs

Candy Pool

Code Builder

Follow the Code

Monsta Munchies

Fox Journey

Piece of Pie

Connect

Fluffy Cuddlies

Color Fill

Liquid Sort

Push Pull Blocks

Spot the Difference

Lost Joe

Blue Turn

Checkers

Flowers

Jewel Routes

Klocki

Number Path

Spatial Rescue

Adventure Tom

Aqua Thief

8 Square

Box Rotate

Laser Maker

Animal Memory

Monsterjong

Rainbow Tower

Bloxorz

Electrio

Red

Me and the Key

Me and the Key 2

Doggnation

Duck Think!

Full Moon

A Bark in the Dark

Factory Balls

Factory Balls 2

Factory Balls 3

Space is Key

Space is Key 2

Layer Maze

Layer Maze 2

Layer Maze 3

Layer Maze 4

Layer Maze 5

Veggi Rabbit

Robotion

Shift the Block

Brixx

Jon Lightning

Zippy Boxes

ClickPLAY Time 6

Hook

Froggy's Pond

Boxed

Jelly Collapse

Tube Master

Light Rays

Sum Blocks

Overlap Sums

Sum Stacks

Number Sequence

Snoring Pirates

Jelly Slice

Reflector

Brain Trainer

Block Turns

Crazy Balls

Golden Scarabaeus

Break the Code

Sum Links 2

Peg Jumper

Pet Party

Tetra Squares

Mancala

Tip Tap Tile

One Clown Standing

The Warehouse

Stones of the Pharoahs

Tangrams

Four in a Row

Piggy in the Puddle 2

Brain Patterns

Capture and Turn

Red Swap Blue

Memory Artist

How to Feed Animals

Draw in Code

Bubble Blaster

2nd Grade Math | Free, Online Math Games

Kindergarten

1st Grade

2nd Grade

3rd Grade

4th Grade

5th Grade

6th Grade

Fun Games for Kids

2nd Grade Math Games

Game Spotlight: Canoe Puppies

Multiplayer Math Games

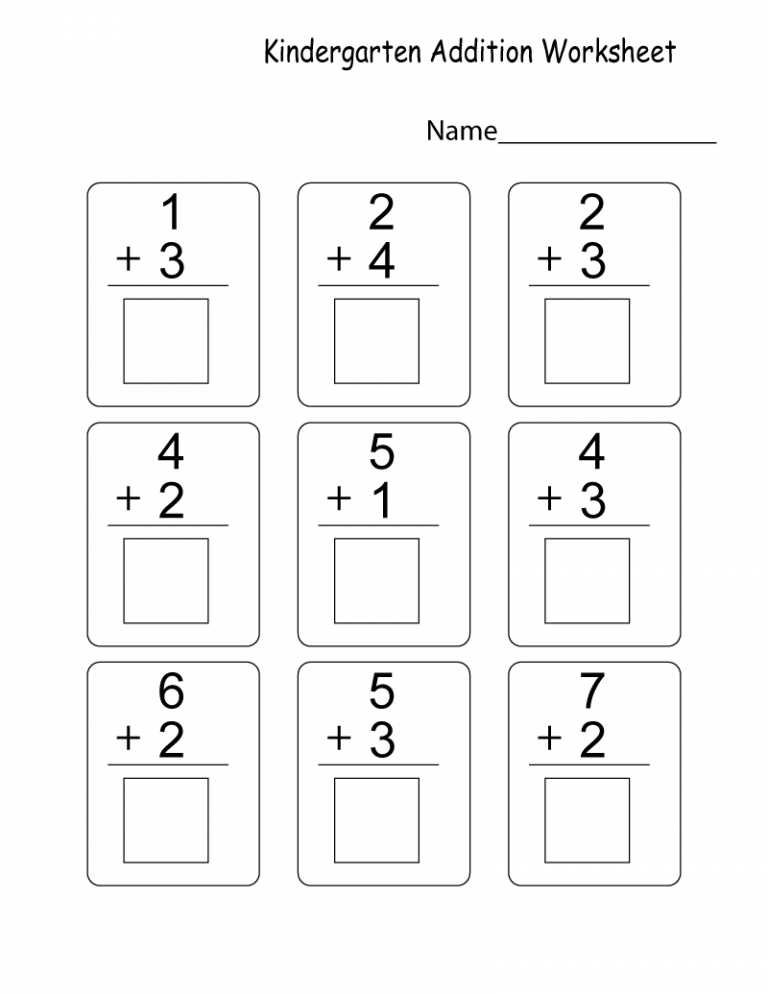
Jet Ski Addition

Money

Time

Tug Addition

Ducky Race Subtraction

Sailboat Subtraction

Island Subtraction

Skateboard Pups

Kitten Match

Shape Names

Time

Money

Operations and Algebraic Thinking

Skateboard Pups

Thinking Blocks Jr

Thinking Blocks

Monster Stroll

Bridge Builder

Code Sums

Kitten Match

Alien Addition

Galaxy Pals 20

Math Monster Subtraction

Addition Facts

Math Racer Addition

Missing Digits Subtraction

Ducky Race Subtraction

Sailboat Subtraction

Math Surpass Compare

Take the Cake Addition

Galaxy Pals 100

Monster Mischief

Addition Blocks

Magic Triangle

Number Trails Addition

Addition Snake

Missing Digits Addition

Island Chase Subtraction

One Sum

Jet Ski Addition

Number Bonds II

Math Monster Addition

Minus Mission

Tug Team Addition

Subtraction Facts

Zogs and Monsters +

Math Word Problems

Skip Counting Video

Multiplication Video

Bridge Builder X

Number Bonds 10 to 20

Number and Operations in Base Ten

Tandem Turtles Rounding

Bingo Tens

Space Jaunt Rounding

Find the Bus Stop

Superhero Subtraction

Bingo Hundreds

Place Value Game

Number Patterns

SumBots

Treasure Quest Numbers

Addition Chart

Place Value Party

Untamed Number Names

Bingo 3 Numbers

Treasure Quest Addition

Hundreds Chart

Bingo Number Pairs

Chain Sums

Addition

Amusement Park Addition

Subtraction

Bingo Rounding

Canoe Puppies

Whole Numbers

Math Bars

Place Value Video

Subtraction Video

Addition Video

Advanced Addition Video

Measurement and Data

Clocks

Time

Time Video

Picture Graphs Video

Time

Money

Candy Cashier

Bar Graphs Video

Bar Graphs Video 2

Geometry

Pattern Blocks

Geoboard

Shape Names

Tangrams

Shapes

Where are the Aliens?

Find the Point

Reflection Painter

Rotation Painter

Super Math Puzzles

Triangle

Triangle Pro

Undercover

Undercover Pro

Pyramid

Pyramid Pro

Pyramid Double

Number Chart

Number Chart Pro

Grid Junior

Grid Pro

Grid X

Function Machine

Logic and Problem Solving Games

Squirrel Hop

Pingu and Friends

Cake Topping

Katana Fruit

Mila's Magic Shop

Pac Rat

Playful Kitty

Piggy Bank Adventure

Jumpy Kangaroo

Icy Super Slide

Arcade Golf

Rabbit Samurai 2

Duck Life 4

Icy Purple Head 2

Duck Life Space

Doctor Acorn 3

Doctor Acorn 2

Arty Agent

Block the Pig

Car Park Puzzle

Red Block Returns

Connect the Roads

Cross the Bridge

Mazes and Keys

Mini Golf World

Sophia's World

Aqua Thief

Monsterland 4

Monsterland 5

Find the Robot

Robot Maze

Chef Slash

One Liner

Puzzle Ball

Double Up

Logic Tail

Robot Islands

The Parking Lot

Feed That Thing

Trap the Mouse

Hex Blocks

2048

Dots and Boxes

Sorting Spheres

Andy's Golf

Islands Of Creatures

Maze Collapse

Gems Glow

Tic Tac Toe

Chess

Ghostie Loners

Animalines

Scratch and Sniff

Reverse the Discs

Candy Pool

Code Builder

Follow the Code

Monsta Munchies

Fluffy Cuddlies

Spot the Difference

Checkers

Flowers

Zippy Boxes

Jelly Collapse

Tube Master

Filltracks

Number Sequence

Snoring Pirates

Jelly Slice

Brixx

8 Square

Paint the House Blue

Number Path

Find the Differences

Liquid Sort

Animal Memory

Monsterjong

Rainbow Tower

Peg Jumper

Tetra Squares

Mancala

Tangrams

Four in a Row

Piggy in the Puddle 2

Capture and Turn

Memory Artist

Rabbit Samurai

Unpuzzle 2

Temple Crossing

Unpuzzle

Color Match

Dot 2 Dot

Puzzle Blocks

Puzzle Slide

Word Games

Letter Recognition

Word Recognition

Typing Jets

Spelling Bees

Double Vowels

Spelling Words

0003

By clicking the "Send" button, you confirm that you consent to the site administration to process and transfer your personal data to the site administration in the framework of the Federal Law of July 27, 2006 No. 152-FZ "On Personal Data" (as amended) and receive response by phone, internet or mail.

media about us

Certificate | Level 1 (5-6 years) | Level 2 (6-7 years) | How are the classes | Ask a question

Today we often hear that the first grade program is complex and voluminous for a child who does not have basic literacy skills and elementary mathematical concepts, it is very difficult to master the first grade course. This is especially true of specialized schools, lyceums and gymnasiums.

Therefore, it is better if the child comes to school prepared. It will be easier for him to get involved in the learning process, he will be more comfortable, and learning will be easy.

It should be noted that the peculiarity of the program "Mathematics" in Russian for preschoolers in the language centers "Polyglotiki" is that it is an organic part of the general course of mathematics, ensuring continuity at all stages.

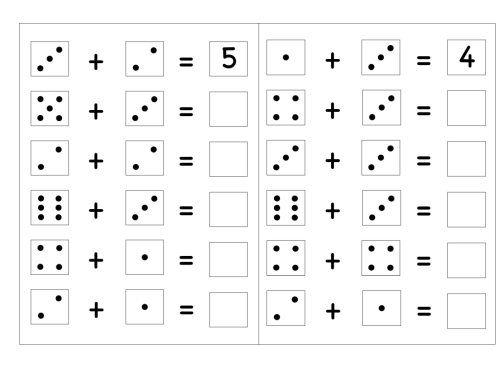
Mathematics program is built taking into account the age and psychological characteristics of preschoolers, takes into account the trends in the modernization of Russian education.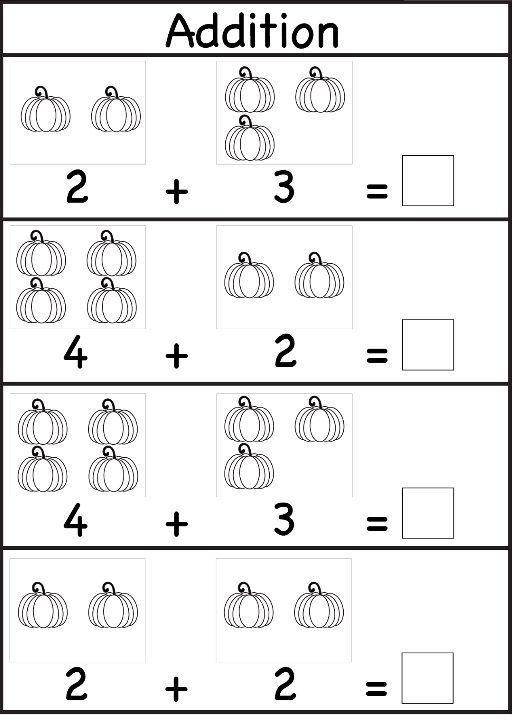 Each exercise and task is aimed at developing and improving logic, children can work with addition and subtraction examples automatically, without any effort. Classes are structured in such a way that one type of activity is replaced by another, during breaks children can play. The duration of the lesson is 45 minutes. This allows you to make the work of children dynamic, rich and less tiring.

Certificate

Level 1 (5-6 years)

Mathematics training at the 1st level of education should result in the following skills:

identify similarities and differences between objects and sets
combine aggregates into one whole, select a part.
compare numbers within 10, determine how much one number is greater or less than another.
perform mathematical operations, write down examples.
use a numeric line.
compare items. Measure quantities.
recognize geometric shapes, find similar ones, design objects.

2nd level (6-7 years)

Mathematics training at the 2nd level of education should result in the following skills:

combine aggregates into one whole, highlight a part.
compare numbers within 20, determine how much one number is greater or less than another.
perform math operations, write down examples within 20, and perform addition and subtraction operations with tens.
compare objects, measure quantities.
recognize three-dimensional geometric shapes, find similar ones, design objects.
navigate in time, call the time, looking at a mechanical watch.

This program is designed for 72 hours: 36 hours - the first level (5-6 years old) and 36 hours - the second level (6-7 years old) and involves the development of both subject and general educational skills in children: organizational, intellectual, communicative , estimated. Children develop not only the necessary mathematical representations, but also speech, thinking, memory, attention, the ability to work in contact with a teacher and other children.

Mathematics lessons

Preschool children are taught in the form of games, interesting and fun tasks that do not overload with boring counting, but allow them to learn the basic concepts and techniques of adding and subtracting numbers.

In the process of teaching the Mathematics course, teachers use a variety of materials that help to perfectly train counting and numbers, which is very important for a preschooler. Mathematical exercises, games and riddles for addition and subtraction are widely used. The child learns to work from pictures and tables, memorize elements, shapes and colors, and continue the logical series of elements. Each task is aimed at working out a burdened mathematical operation.

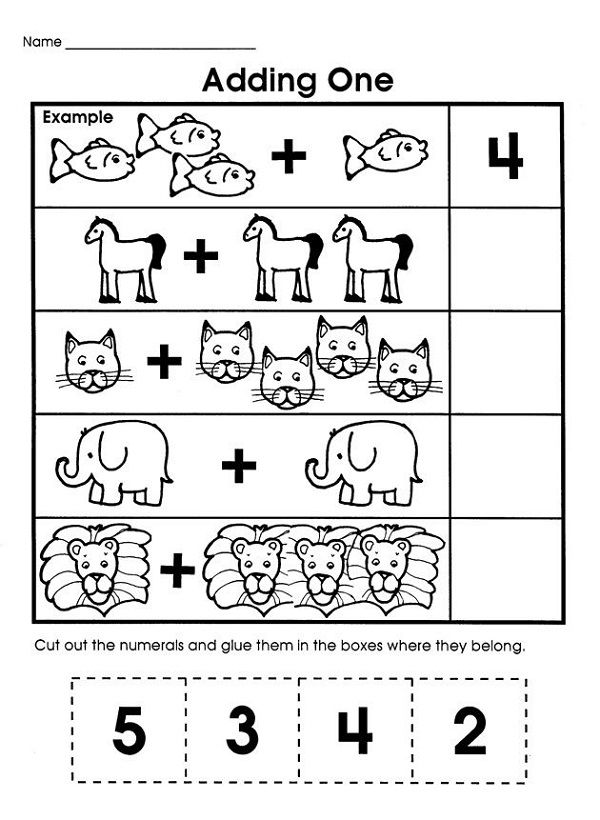
Scientific works in the field of pedagogy speak of the importance and necessity of developing logic and mathematical thinking in schoolchildren, especially in primary school. Regular practice allows children to develop the skill of quickly and efficiently working with numbers: schoolchildren can count, solve problems, and do homework much easier and faster. The main objective of our developing course is not only to teach how to perform mathematical exercises, tasks, to master counting, numbers, but also to apply an integrated approach to developing important logical abilities.

The ability of preschoolers to easily distribute figures depending on color, shape and other features indicates their readiness to move on to more complex tasks. So, the methodologists of the Polyglot Center within the framework of the course “Mathematics” have developed special materials with the help of which we can develop in a child the ability to deft and skillful counting. Learning has a positive effect not only on the ability to count, but also develops logic, thinking and memory.

Parents and children usually face the first difficulties already at school. Not everyone is comfortable with math. A first-grader is bombarded with a huge amount of new information that needs to be learned. Also, in the classroom, the ability to write correctly, monitor the position of the hand, see the differences in letters and words, easily know and assimilate school material is developed

Course of studyEnglish languageGerman languageSpanish languageItalian languageChinese languageFrench language Preparing for school Preparing for examsArtCookingCraftsFitnessMusicStorytimeYoga kidsEnglish Literature English for elementary school (online)English Club-GardenEnglish TheaterEnglish language (group)Bilingual full-time kindergartenKids School of FashionArt StudioKorean languagePrivate lessons with PolygraphyKalliglot Memory developmentSummer campSpeech therapy classesMath in EnglishMental arithmeticMini-gardenMnemonicsMusical DevelopmentScience in EnglishWrite-ReadPreparation for immigration PortugueseConversation Club with a native speakerEarly development in EnglishSpeed readingCreativity in EnglishLearn well!Fitness in EnglishChess ClubEnglish (online)German (online)Spanish (online) )

For faster processing of the application, you can provide more information. Specify

By clicking the "Submit" button, you confirm that you consent to the site administration to process and transfer your personal data to the site administration in the framework of the Federal Law of July 27, 2006 No. 152-FZ "On Personal Data" (as amended) and receive a response by phone, internet or mail.

Choose your branch:

Russia
Kazakhstan
Azerbaijan

All Polyglot branches

Callback

Goals and objectives of the mathematical development of preschoolers. The value of teaching children mathematics

Purpose:

To formulate the main goals and objectives of the mathematical development of preschoolers.

Show the role of teaching mathematics for the comprehensive development of the child's personality.

The problem of teaching mathematics in modern life is becoming increasingly important. This is explained, first of all, by the rapid development of mathematical science and its penetration into various fields of knowledge.

Increasing the level of creative activity, problems of production automation, modeling on electronic computers, and much more presuppose that specialists in most modern professions have a sufficiently developed ability to clearly and consistently analyze the processes being studied. Therefore, training in kindergarten is aimed primarily at educating children in the habit of full-fledged logical argumentation of the environment. Learning experience indicates that the development of logical thinking in preschoolers is most facilitated by the study of elementary mathematics.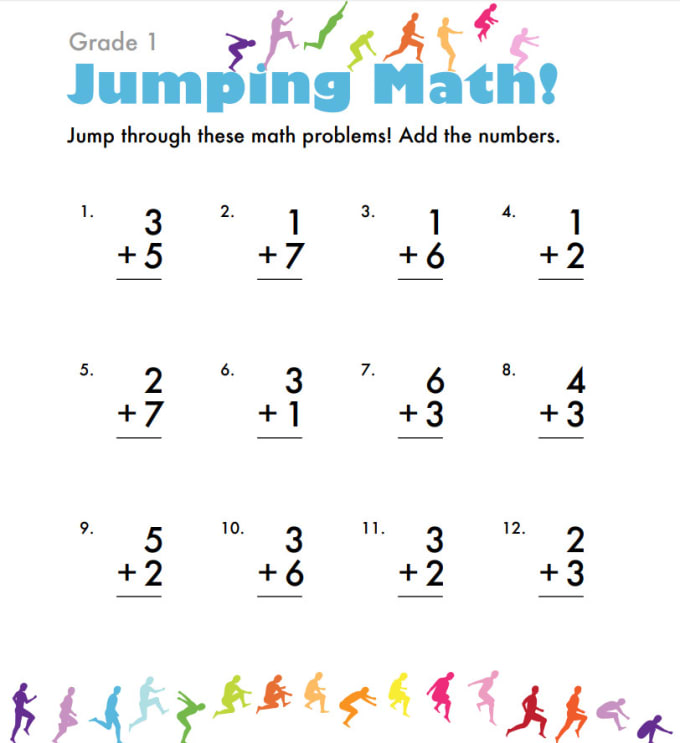 The mathematical style of thinking is characterized by clarity, brevity, dismemberment, accuracy and logic of thought, the ability to use symbolism. In this regard, the content of teaching mathematics at school and kindergarten is being systematically restructured.

Naturally, the basis of knowledge is sensory development, acquired through experience and observation. In the process of sensory cognition, representations are formed - images of objects, their properties, relationships. So, operating with a variety of sets (objects, toys, pictures, geometric shapes), children learn to establish equality and inequality of sets, to call the number of words: “more”, “less”, “equally”. Comparison of specific sets prepares children for the subsequent assimilation of the concept of number. It is operations with sets that are the basis that children turn to not only in kindergarten, but also throughout the subsequent years of schooling. The idea of a set forms in children the basis for understanding an abstract number, the laws of a natural series of numbers. Although the concepts of a natural number, as well as a geometric figure, magnitude, part and whole are abstract, nevertheless they reflect the connections and relationships of objects in the surrounding reality.

It has been proven that familiarizing children with different types of mathematical activities in the process of purposeful learning orients them to understanding connections and relationships. The formation of initial mathematical knowledge and skills in preschool children should be carried out in such a way that training gives not only an immediate practical result (counting skills, performing elementary mathematical operations), but also a broad developmental effect. As a rule, the mathematical development of preschoolers is understood as qualitative changes in the forms of cognitive activity of the child, which occur as a result of the formation of elementary mathematical representations and the logical operations associated with them. An analysis of scientific research (A.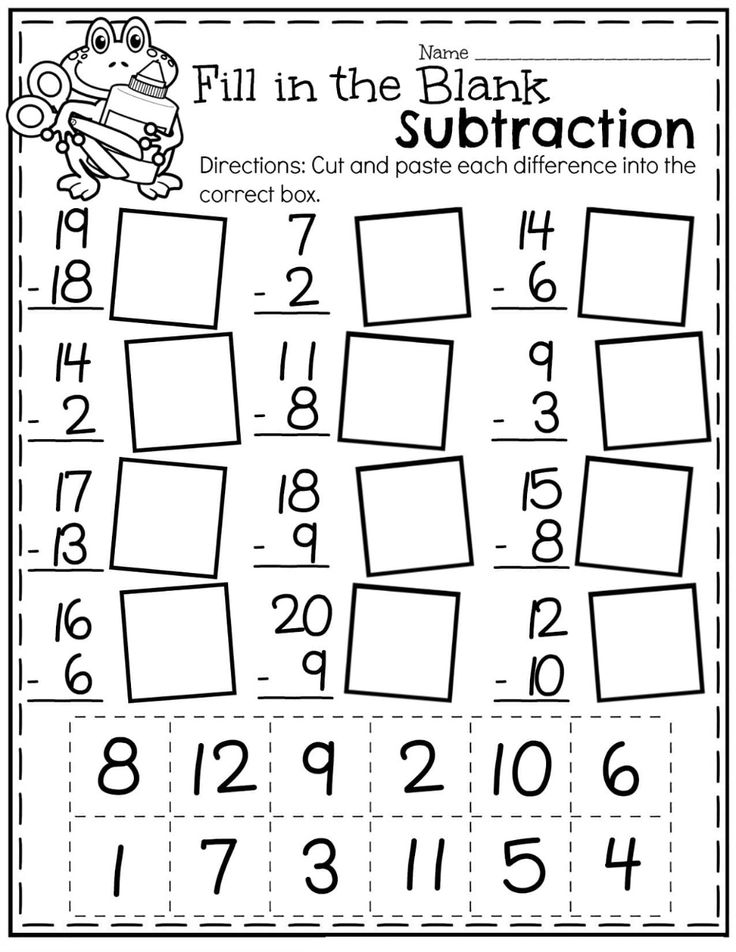 M. Leushina, N.I. Nepomnyashchaya, A.A. Stolyar, etc.), pedagogical experience convinces us that rationally organized teaching of mathematics to preschool children ensures the overall mental development of children. (Rationally organized education is timely, appropriate for the age and interests of children.) At the same time, pedagogical guidance from an adult (educator or parents) is important. Children acquire elementary knowledge about the multitude, number, size and shape of objects, learn to navigate in time and space. They master the account and measurements of linear and volumetric objects with the help of conditional and generally accepted measures, establish quantitative relationships between quantities, the whole and parts.

In the mathematical preparation of children, the development of elementary mathematical concepts, an important role is played by the teaching of measurement as the initial way of knowing the quantitative characteristics of the environment. This makes it possible for preschoolers, first of all, to use not generally accepted, but conditional measures when measuring bulk, liquid substances and lengths. At the same time, children develop an eye, which is very important for their sensory development.

In the process of systematic teaching of mathematics, children master special terminology - the names of numbers, geometric shapes (circle, square, triangle, rhombus, etc.), elements of figures (side, top, base), etc. However, it is not recommended when working with children to use such words-terms as “natural glad”, “set”, “structure”, “elements of the set”, etc. At the same time, work is not limited only to classes. It should be borne in mind the use of the entire didactic space in an educational situation.

Mathematics classes are of particular importance in connection with the development of children's cognitive interests, the ability to show strong-willed efforts in the process of solving mathematical problems.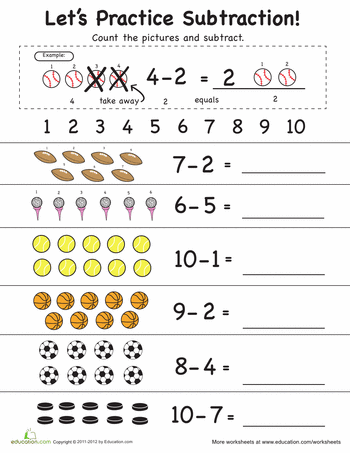

As a rule, educational tasks in the classroom are solved in combination with educational ones. So, the educator teaches children to be organized, independent, listen carefully, do the work efficiently and on time. This disciplines children, contributes to the formation of their focus, organization, responsibility. Thus, teaching children mathematics from an early age ensures their comprehensive development.

Among the tasks for the formation of elementary mathematical knowledge and the subsequent mathematical development of children, the main ones should be distinguished, namely:

acquisition of knowledge about set, number, size, form, space and time as the foundations of mathematical development;
formation of a broad initial orientation in the quantitative, spatial and temporal relations of the surrounding reality;
formation of skills and abilities in counting, calculations, measurement, modeling, general educational skills;
mastery of mathematical terminology;
development of cognitive interests and abilities, logical thinking, general intellectual development of the child.

These tasks are most often solved by the teacher at the same time in each lesson in mathematics, as well as in the process of organizing various types of independent children's activities. Numerous psychological and pedagogical studies and advanced pedagogical experience in preschool institutions show that only properly organized children's activities and systematic training ensure the timely mathematical development of a preschooler.

Numerous studies (A.M. Leushina, N.A. Menchinskaya, G.S. Kostyuk and others) have proved that the age capabilities of preschool children allow them to form scientific, albeit elementary, initial mathematical knowledge. More precisely, children acquire elements of mathematical knowledge. At the same time, it is emphasized that in accordance with the age of the child, it is necessary to select the forms and method of education. In this regard, at specific age stages, the most favorable conditions for the formation of certain knowledge and skills are created.

So, in the second junior group of the kindergarten (the fourth year of life), the main attention is paid to the formation of knowledge about the multitude. The concept of a set is one of the basic and most general, it runs through all of mathematics. The concept of a set is so broad that it is not defined even at the modern level of development of science, but is introduced as the original one and explained with specific examples. In the middle group, in the process of studying the basic properties of a set, the concept of a number is formed, and in the older group, the first ideas about the natural series of numbers are formed. At preschool age, the understanding of the basic properties of the set is limited. However, awareness of its individual properties (equality and inequality, independence of the power of a set from its qualitative features) is possible already at a younger preschool age.

Along with the formation of initial mathematical concepts and concepts, the kindergarten education program provides for familiarization of preschool children with a number of mathematical dependencies and relationships. So, children are aware of some relationships between sets (equal power - uneven power; order relations in a series of quantities, natural numbers; spatial and temporal relations, etc.). At the same time, all mathematical knowledge is presented in interconnection. For example, the formation of ideas about quantity is associated with the formation of ideas about the multitude and size of objects with the development of the ability to see, conditionally determine the size, parameters, as well as the assimilation of relationships between objects. It must be borne in mind that, while acquiring knowledge about number, children learn to abstract quantitative estimates from all others (color, shape, size).

The formation of initial mathematical knowledge in interconnection allows you to gradually and purposefully concretize and refine each of the selected properties. Familiarization of children with the measure and measurements contributes to the formation of a more accurate understanding of the number, and above all the unit. It is the connection of counting and measurement that helps the child to realize the dependence of the result of counting (measurement) on the unit of counting (conditional measure).

Mathematics classes in kindergarten form the simplest types of practical and mental activities of children. Under the types of activity - in this case, methods of examination, counting, measurement - they understand the objective sequential actions that the child must perform in order to assimilate knowledge: element-by-element comparison of two sets, imposing measures, etc. Mastering these actions, the child learns the purpose and methods of activity, as well as rules that ensure the formation of knowledge. For example, comparing equal and unequal sets, superimposing or applying elements, the child is aware of the concept of quantity. Therefore, special attention is paid to the development of practical actions of children with objects.

The central task of the mathematical development of children in kindergarten is learning to count.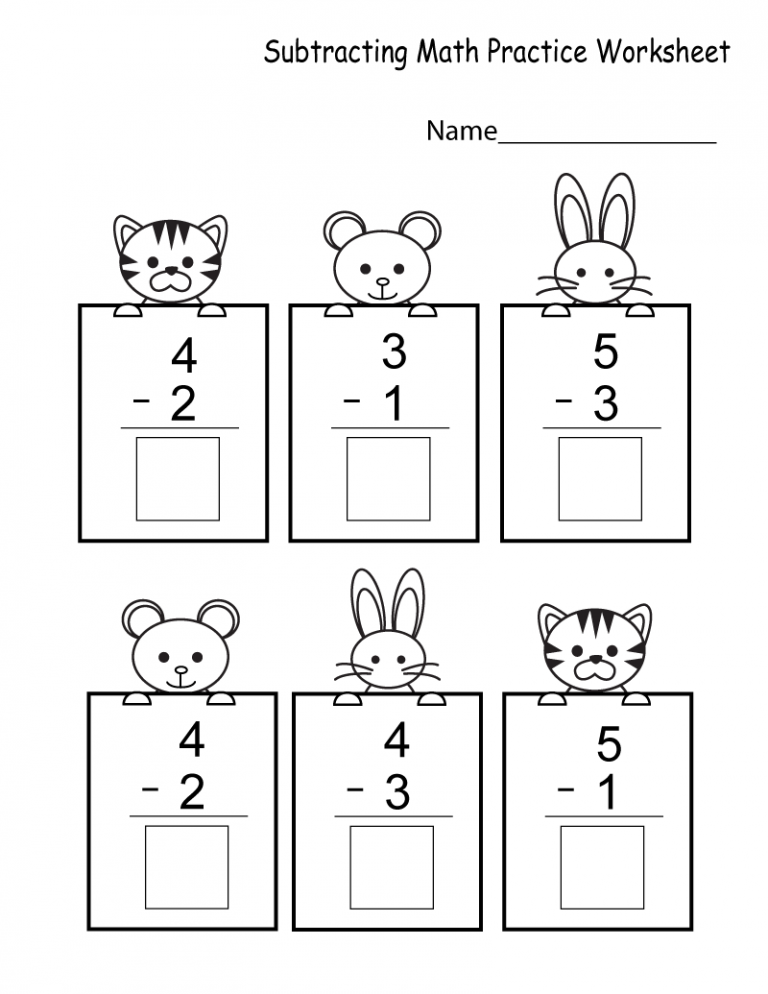 The main methods in this case are imposition and application, the mastery of which anticipates learning to count with the help of numeral words.

At the same time, preschoolers are taught to compare objects by size (size) and designate the results of the comparison with the corresponding words-concepts (“more - less”, “narrow - wide”, etc.), build rows of objects according to their size in ascending or decreasing order (large , small, even smaller, smallest). However, in order for the child to learn these concepts, it is necessary to form specific ideas in him, teach him to compare objects with each other, first directly - by superimposing, and then indirectly - with the help of measurement.

The kindergarten math program provides for the development of children's eye in determining the size of objects. To do this, they are trained to evaluate the size (size of objects) as a whole or by individual parameters, comparing with the size of known objects.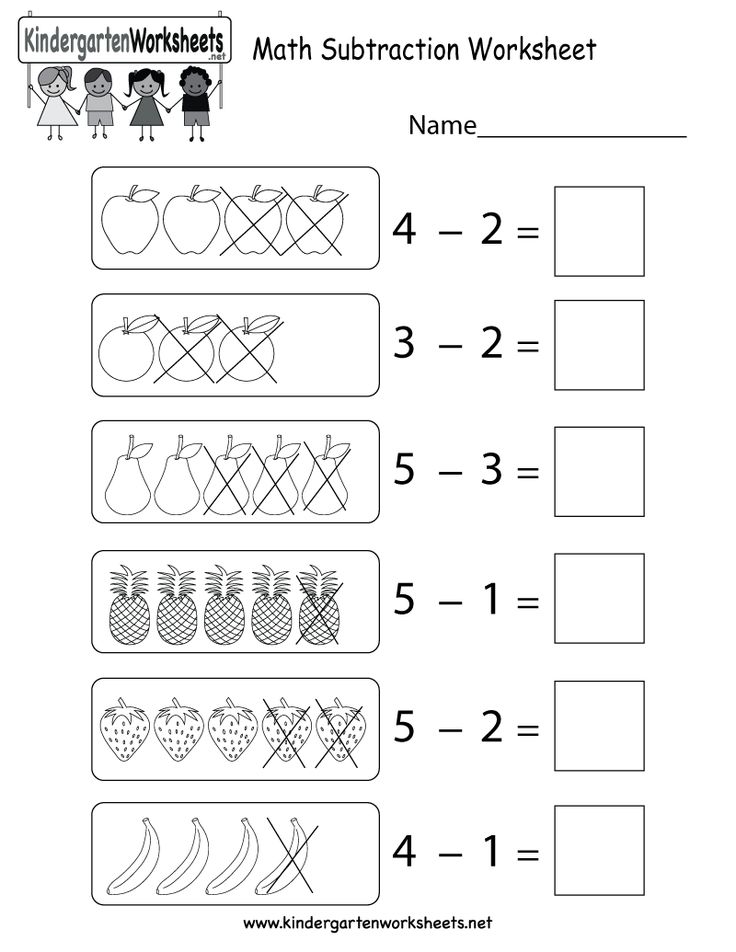 Attention is drawn to the formation of the ability to check the correctness of the assessment in their practical activities, using additions, reductions, etc. Each practical action replenishes the knowledge of children with new content. It is proved that the formation of elementary mathematical knowledge occurs simultaneously with the development of their practical skills and abilities.

Practical actions, while playing a certain role in the mathematical development of children, do not themselves remain unchanged. Thus, the activity associated with the account is changed. At first, it relies on a practical element-by-element comparison of two concrete sets, and later, a number as an indicator of the power of a set and a natural series of numbers acquires special significance, which subsequently replaces one of the concrete sets.

First, children take objects with their hands, shift them, and then count the objects without touching them, or perceive them only by touch.

On the basis of practical actions, children develop such mental operations as analysis, synthesis, comparison, generalization. The teacher should be guided in evaluating the results of his work primarily on these indicators, on how children are able to compare, analyze, generalize, and draw conclusions. The level of children's mastery of mental operations depends on the use of special methodological techniques that allow children to exercise in comparison, generalization. So, children learn to compare sets by quantity, while carrying out a structural and quantitative analysis of the set. Comparing objects by shape, children identify the size of individual elements, comparing them with each other.

An important task is the development of thinking and speech in children (mastery of mathematical terminology). Much more attention should be paid to the development of the initial skills of inductive and deductive thinking, the formation of children's cognitive interests and abilities. It should be noted that general methods of cognition form the basis of any scientific thinking, including mathematical. Naturally, the latter has its own special significance.

In practice, there is often a one-sided understanding of abilities as highly specialized, which borders on giftedness. In this regard, educators sometimes underestimate the formation of general cognitive abilities in all children. Any activity is impossible if a person does not have the ability to do it. In psychology, abilities are designated as personality traits necessary for the successful performance of an activity. The educator needs to know what exactly these abilities are, what mental properties the chosen activity will require and without which it is generally impossible.

Abilities should be considered not only in connection with a certain type of children's activity, but also in connection with its general structure, in which, first of all, orienting and performing actions are distinguished.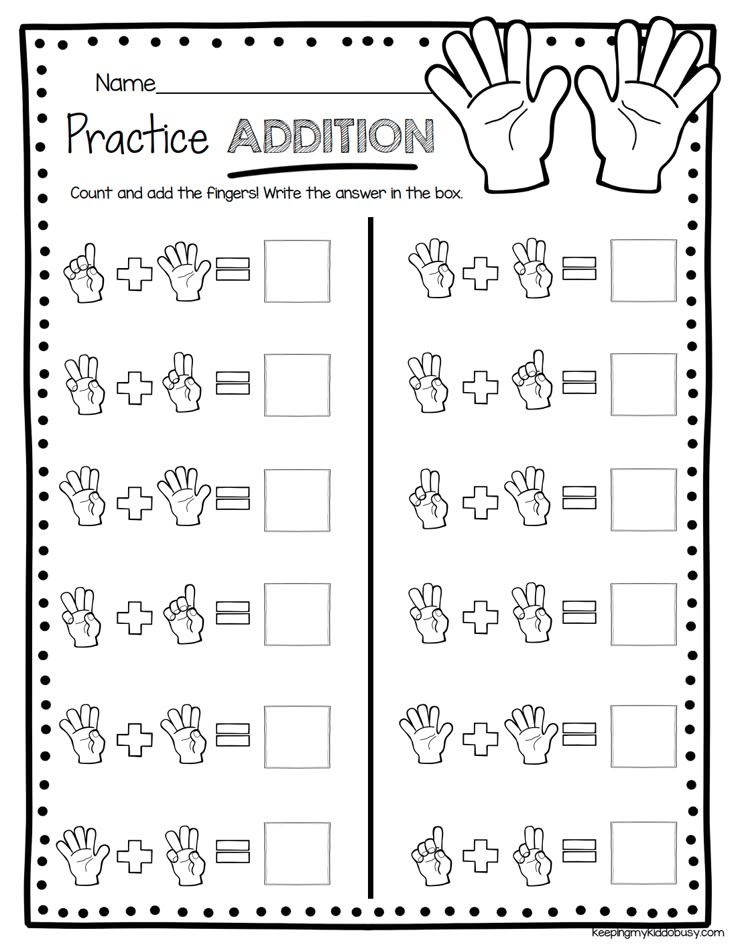 And when we talk about general abilities for activity, we mean how much a child is able to use his knowledge, skills, and what level of cognitive independence he has. All this determines the effectiveness of the performing part of the general abilities. Along with this, it is necessary to form in children the ability to abstract, to highlight the main thing.

So, the mathematical development of children involves a broad program of introducing them to activities, in this case, mathematical, which is led by an adult (teacher, parents).

Tasks of the methodology of mathematical development as a scientific field:

1. Scientific substantiation of the program requirements for the level

of the formation of mathematical representations in preschoolers in each age group

2. Determination of the content of mathematical material for

teaching children in preschool.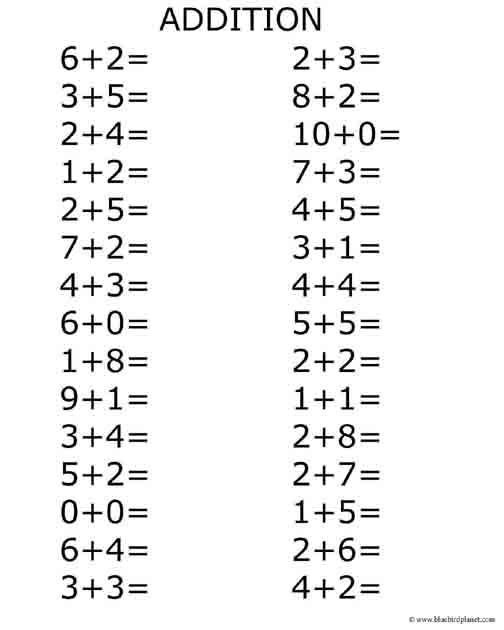

3. Development and implementation in practice of effective didactic tools, methods and various forms of organization of work on the mathematical development of children.

4. Implementation of continuity in the formation of mathematical representations in preschool educational institutions and at school.

5. Development of the content of the training of highly specialized personnel capable of carrying out work on the mathematical development of preschoolers.

6. Development of guidelines for parents on the mathematical development of children in a family.

The purpose of the mathematical development of preschoolers

• Comprehensive development of the child's personality.

• Prepare for success in school.

• Correctional and educational work.

Problems of mathematical development of preschoolers

1.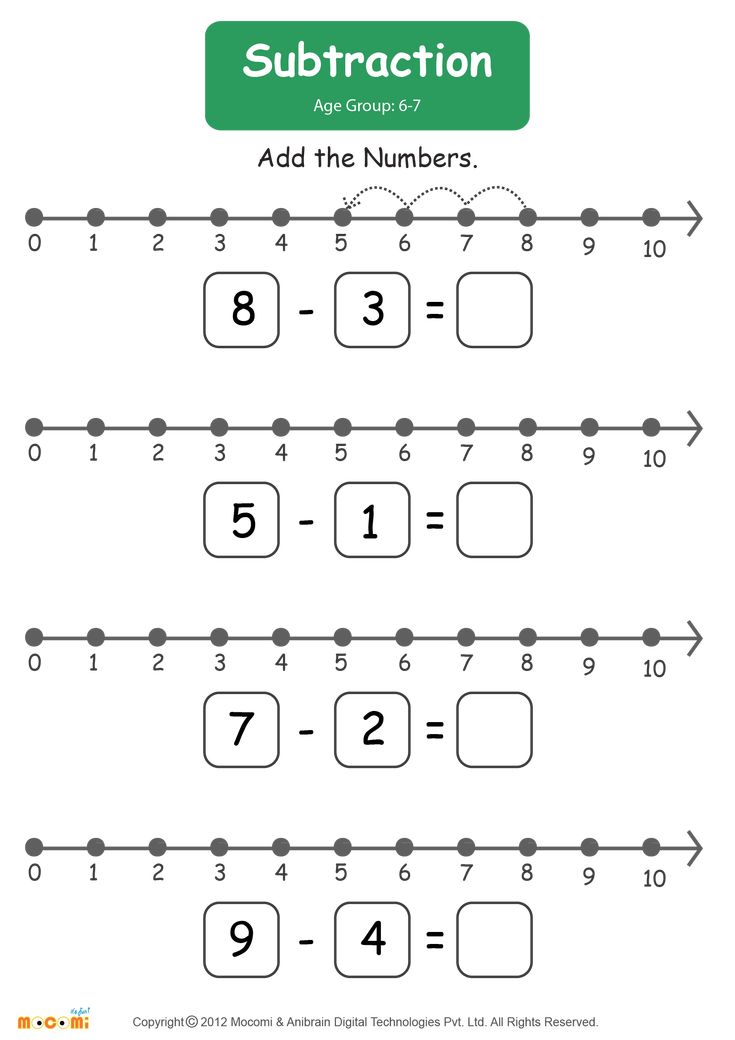 Formation of a system of elementary mathematical representations.

2. Formation of prerequisites for mathematical thinking.

3. Formation of sensory processes and abilities.

4. Expanding and enriching the vocabulary and improving

related speech.

5. Formation of initial forms of educational activity.

Education leads development, is the source of development.

Learning must go ahead of development. It is necessary to focus not on what the child himself is already capable of doing, but on what he can do with the help and under the guidance of an adult. L. S. Vygodsky emphasized that it is necessary to focus on the “zone of proximal development”.

Well-ordered ideas, well-formed first concepts, well-timed mental abilities are the key to further successful education of children at school.

Psychological research proves that in the process of learning there are qualitative changes in the mental development of the child.

From an early age, it is important not only to communicate ready-made knowledge to children, but also to develop the mental abilities of children, teach them to independently, consciously acquire knowledge and use it in life.

Learning in everyday life is episodic. For mathematical development, it is important that all knowledge is given systematically and consistently. Knowledge in the field of mathematics should become more complicated gradually, taking into account the age and level of development of children.

It is important to organize the accumulation of the child's experience, to teach him to use standards (forms, sizes, etc.), rational methods of action (counting, measurements, calculations, etc.).

Given the little experience of children, learning proceeds predominantly inductively: first, specific knowledge is accumulated with the help of an adult, then they are generalized into rules and patterns.

Learn more