Teaching number recognition to preschoolers

Number Recognition – The Best 16 Games To Teach It (+ Tips) – Early Impact Learning

In the ten years I have spent teaching young children between the ages of 3 to 5, one of the most important secrets I have discovered is how to teach recognizing numbers.

Some children will just pick this up from exposure to numbers in their environment. However, for most children this a long process, and needs some real expertise and strategies to get them confidently recognizing numbers. This is where this article comes in!

So, for the short answer, how do you teach children to recognize numbers?

Teach children to recognize numbers by using fun stories or chants for each number. Practise sky-writing the number in air, drawing it in foam or other messy play substances, and by making numbers in craft activities. Seeing numbers throughout their play is crucial.

That’s the simple version, but there is just so much more to it than that!

In this article I have condensed ten years of trial and error into 17 tried and tested strategies that you really should try to get children recognizing numbers.

Pretty much all of these games can be used either at school or nursery, or at home. Good luck!

1.Use Stories For Each Number

A great way to introduce stories to start with is with storytelling.

Stories are great for teaching lots of different skills, as stories really tap into children’s sense of curiosity and attention like few other things.

One way to do it is have a bag of a few objects. If you are introducing number 3, for example, you could say something like ‘This is number 3. Today it went on an adventure. It found 3 magic stones.’ (Take them out of the bag). ‘It rubbed the stones, and out popped 3 frogs.’ (Take the toy frogs out of the bag).

It is good to spend time during the story looking at what the numeral looks like, and getting them to draw it in the air, or on their hand.

2. Number Stones

Beautiful materials help in the teaching of anything, and these number stones are certainly a fantastic natural resource.

All you need for these are some pebbles. I happened to find some excellent white, sparkly stones by chance, that the children really love.

The idea is to write or paint some numbers on some of the stones. There are other things you can do, like create stones with quantities on as well. For example, I have created these stones with different numbers of bugs on:

These stones are great for some of the following things:

• Finding objects, such as 3 pine cones, and matching to the right numeral

• Match numeral stones to quantity stones, e.g. 4 bugs to the number 4

• Trying to copy a number line and put them in order.

This activity is just one of many exciting ways to use stones and pebbles for learning. To find out a whole load more, you can check out this definitive guide on how to use story stones.

3.Use Chants

There are little fun ditties and chants you can use for each number.

For example, number 3 is:

A curl for you, and a curl for me

That’s how you make number three!I have used chants that I just found on the internet before. For example, this video has some excellent ones you can use:

Also, children really love this song when it comes to numeral formation:

4.Have Number Actions

Many children learn letters through actions when they do phonics, so why wouldn’t the process work for numbers.

The good news is – it does work!

Multisensory learning is definitely the way to go when you are teaching things like recognizing numerals or sounds. It activates a lot more of the brain if you have movements, sound and visuals all mixed together.

The number actions I use I have just invented. They go like this:

0 – Make a circle with your fingers

1 – Throw one arm straight up

2 – Two arms up

3 – These are like Mickey Mouse ears on their side. Put your head to one side, and put Mickey Mouse ears on top (honestly the sideways ears do look like mouse ears)

4 – I get them to cup both hands round their mouths and call ‘Four!’ This is like when a golfer loses their ball and calls ‘fore!’

5 – Show five fingers

6 – Put two fingers up high in the air. This is the signal in cricket for a ‘six’. Apologies to my American friends that I know read this blog in droves! If you have no idea what this means, please feel free to invent your own action for six.

7 – Do a salute with your hand. Your arm will have made the shape of a ‘seven’.

8 – Pretend to hold two apples, one on top of the other. Put them to your mouth and say ‘eight’ (as though you just ‘ate’ the apples)

9 – Put your hand vertically underneath your head with your fingers on your chin. It looks like your head is on your arm, like a lollipop. I looks a bit like a nine – a stick and a circle

10 – Two sets of hands thrown forwards (with ten fingers)

Using actions such as this works a treat for teaching numbers, and is also an excellent way to teach phonemes (sounds) as well.

5.Skywrite Numbers

Skywriting is another great multisensory experience.

It is good if you can show them what the numbers look like on something – maybe a chalkboard, interactive board, or written on big pieces of paper.

The simplest way of skywriting is to stand up, and use your finger in the air to draw the numbers. Make them as big as you can! (i.e. get the children to bend their knees, and stretch up high respectively)

You can make the experience even more exciting by:

• Using ribbons or streamers to draw the numbers in the air

• Skywrite to music!

• Use puppets or toys in their hands to write with

6.

Books are another route to firing up children’s curiosity and interest.

The idea of this strategy is that you find opportunities in books to count or find numbers, and then talk about it. You can write the numbers that you find, or link one of the other strategies in this article to the numbers (for example, skywriting the numbers that you find).

There are a mixture of books you can use:

• Many books are clearly about maths, and they have lots of numerals in anyway. These work really well.

• Some books are nothing to do with counting, but you can link numbers to them anyway. You can count the dwarves in Snow White for example, and write the number. You can count the dogs in Hairy Maclary.

7.Loose Parts On Numbers

Decorating numbers, and turning the numerals into fun art activities is a great way to go to get children recognizing them.

One way is to use loose parts to experiment with the formation of numbers.

All you need to do is create some big numbers somewhere, and the children put lots of loose parts like bottle tops or gems and other things over the top of them to make the shapes of the numbers.

You could:

• Draw numbers on big paper

• Chalk them on the floor outside

• Have big wooden numbers

Good loose parts include things like shells, stones, screws, wood slices, pegs, pompoms, and whatever else you can find. If you are looking for ideas of what other materials you can use for loose parts, then I have written an article containing at least 100 ideas, that you can check out here.

8.Number Lines

Number lines are great for children to start to visualize what numbers look like in a sequence. They are also great for number recognition.

Some excellent ways to use them for this purpose include:

• Making number lines in artistic ways. The children can decorate them, or stick numbers onto sticks or something similar

• They can order numbers on a blank line, copying a number line

• Refer to number lines as you sing songs, or do chants. The more they use them the better they will get.

9.Matching Games

Some old-school memory games are great for number recognition. For example, pairs. Have two sets of number cards. I would just focus on the numbers that you are trying to teach, so it could be numbers 1-5 or 0-10.

Place the pairs of cards down, and take it in turns to turn over two and try to find pairs.

Another game that is similar is number bingo.

Matching games like this are quite simply excellent for memory in general. If you want to find out the definitive list of the best preschool memory games for children, then check this out.

10. Number Golf

They really love this one! Many children really enjoy sports, and so if you can tap into this interest then go for it!

There are different ways of doing this, but one easy way is to use big paper. Draw big circles all over the paper – these are the golf holes. Write numbers in these golf holes.

Then all you need is a golf club and a ball. I normally use a small playdough ball that you roll yourself, and the club can be something like a lolly (popsicle) stick.

Hit the ball around the golf-course and try to get it into the holes. This is great for number recognition. You can also:

• Go in order like a real golf course

• Recognize numbers beyond ten

• Try a big outdoor version using large rubber balls and huge circles drawn with chalks. You could kick or roll the balls

Playdough games like this are brilliant for fine motor.

11. Messy Number Formation

The messier numbers can get the better!

The idea is here is to get some kind of messy surface that the children can mark-make numbers on.

You could use:

1. Shaving foam
2. Shaving gel
3. Porridge oats
4. Glitter (if you’re feeling brave as this will be very messy!)
5. Flour
6. Sand

Have some big numbers for them somewhere to look at and copy. The children try writing the numbers in the messy substance! Hours of fun.

12. Put Numbers On Construction Toys

Another good strategy to teach numbers is to find out what the children enjoy doing anyway, and just add some numbers to these activities.

A good example is construction toys. Lots of children love using lego and building blocks, and lots of other things like this. Why not add some numbers to these resources?

For example, you can write some numbers on some old building blocks. Can they put them in order?

Can they build numbers out of construction toys?

Can they make a tower using a quantity of blocks that matches a number card?

Tapping into interests is one of the key ways of motivating young children. If you want to find out the definitive list of things you can do to focus pre-schoolers then take a look at this article I wrote about the 15 top strategies.

13. Numbers On Vehicles

Vehicles are another thing that many young children are fascinated by. These offer many opportunities, including:

• Make a car-park. Get a large piece of cardboard or paper, and draw some car park spaces on it with numbers on. If the cars have numbers on anyway, even better! You can match the numbers

• Have races and put the winners on a podium of some description, labelled 1, 2 and 3

• Put vehicles with numbers on in order, maybe following a number line

14. Numbers In Environment

This is a really important way that many children will learn numbers – encountering them in the environment.

There are many things you can do to help the process:

• Point out numbers that you or children may find in the environment, and talk about them. Examples could be numbers on doors or bins, numbers on football shirts, numbers on signs

• Encourage children to count and record in the activities that they do. For example, build a tower and count the blocks. Make a model of an alien and count the arms.

• Include numbers in displays around the room

15. Number Dice Games

Competitions and games with dice really help children to learn now to recognize numbers.

The repetition of seeing numbers again and again really helps, and also a little bit of competition really focusses the minds for some.

Some great games to do with a numeral dice include:

• Roll the number dice and do that number of actions – e.g. clap, jump, hop etc

• Have a simple racetrack drawn on the floor. This could be with chalk outside, or something similar. Have a long line of about ten sections in a line, so that it looks a bit like a ladder. All children start at one end. One rolls the dice and then jumps forward that number of squares. Then the next person goes. It is a race to take it in turns, and get to the end first! There are lots of fantastic outdoor maths games such as this one. Check out 50 of the best ideas here!

• Whack the dough! This is a fantastic playdough game that they really love. What you quite simply do, is first make lots and lots of little balls of playdough. Then you roll the dice and whack that number of balls! This is great for number recognition, and 1:1 counting. Playdough is one of the most exciting resources you can use for early Maths. If you want to learn more playdough maths games, then check these out.

16. Fishing Game

This is a simple adult-led game that they really enjoy.

Get some kind of number cards, and stick a big paperclip to the top. Get a stick such as a broomstick, and tie a string to it. At the end of the string have a magnet tied on.

The idea is to have the number cards in the middle of a circle of children all faced down. One child goes first, and tries to pick up a card with the magnet. Hopefully the magnet will be strong enough. If you are having problems picking them up, then stick more paperclips on the cards!

Fish for a card and then identify what it is!

This is one of the favorite games in my book 101 Circle Time Games…That Actually Work!

This book contains:

-All the best math circle time games

-Phonics and literacy circle time games

-Emotion and mindfulness circle time games

-Active and PE circle time games

-And so much more!

You can check out 101 Circle Time Games…That Actually Work here.

Right, that’s the end of the 16 best games I know to teach recognizing numbers. I’m going to finish with some key questions that many people ask about recognizing numbers.

Common Number Recognition Questions Answered

Why is it important to know number names?

Recognizing numbers is a foundation skill of early maths. It is important to develop before you can go on to many other skills.

Some examples of skills that cannot be attempted without first recognizing numbers includes:

• Ordering numbers in any way

• Finding missing numbers in a sequence

• Being able to add and subtract with written number sentences

How to teach numbers to special needs children?

Many of the same strategies will apply if you are trying to teach numbers to special needs children.

Try to make the strategies as multi-sensory as possible. Actions and physical movement is good to support number recognition.

Please bear in mind that the age and speed with which children will learn numbers will vary greatly if they have any disabilities.

Some children, for example with autism, may learn numbers at a very young age, and number recognition can be an exceptional skill of many autistic children.

At what age should children recognize numbers?

This is a tricky question and really will differ for different children.

In general, children will begin to learn how to recognize numbers somewhere between the age of 2 and 5. It is hard to be more precise than that!

Just because a child learns numbers later than another does not mean that their rate of progress will be slower in the future. It is more an issue of child development rather than an indicator of intelligence.

When are children ready to recognize numbers?

Normally children will display some signs before they start to recognize numbers. These include:

• An interest in numbers in the environment

• They are starting to rote count (or indeed are already good at this skill)

• They are beginning to count objects

Do you teach letters in the same way as numbers?

There are definitely parallels between strategies that work well for both. These include:

• Make it multisensory – the more active and fun the process the more chance they have of learning them

• Use songs, chants and books to help the process

• Repeat and practise what you have learned

Find out more about how letters and sounds are taught here.

Conclusion

The more multisensory you can make number recognition learning the better. Spark children’s curiosity with exciting resources, and get them dancing, moving and singing, and the process becomes fun and effective. Good luck, teaching those numbers!

If you liked this article, then why not try one of these:

• What Is Rote Counting? And How To Teach It
• Symmetry Activities For Kids – 10 Fantastic Activities

Recent Posts

13 Hands-On Number Recognition Games Preschoolers will Love

• Share
• Email

Are you teaching your child to identify numbers? Here are some fun and interactive number recognition games for preschoolers and kindergarteners that you can play at home or in the classroom too.

If you’re wondering how to teach number recognition, the answer in early childhood is always through play.

Play is the natural way in which children learn. During play, children practice their skills and make sense of new knowledge and experiences. They develop early maths skills through play.

Remember that there are many aspects to learning about numbers. There is learning to count, which you can teach with games and counting songs, and then there’s one-to-one correspondence, which is when a child reliably counts one object at a time.

Number recognition is about the physical appearance and shape of a number, as well as what value it represents.

These number recognition activities for preschoolers are a great place to start teaching the numbers from 1 to 10, but once you get going you’ll quickly notice opportunities all around you!

This numbers game can be adapted to suit your child’s age, stage and interests.

Write numbers onto some toy cars and create a parking garage with numbered spaces. Your child can then match the number on the car with the number in the space and park the car correctly.

If he needs more of a challenge replace the numerals with dots or words so that your child can begin to recognise numbers being represented pictorially.

If your child is not particularly interested in cars you could do a similar game with animals, dolls, or whatever it is that your child enjoys playing with.

Put numbers on toy cars, or for a large scale activity; bikes and scooters. Create a car wash for them with clothes, brushes, water and bubbles.

Your child is then in charge of ensuring that the cars, bikes, or scooters come to the car wash and get cleaned in the correct order. As well as recognising numerals, this activity gives your child the chance to begin learning about number order.

This fairground classic is great for numeral recognition. How you set this up is your choice.

If you have lots of ducks and something to hook them with then perhaps you could create a replica of the fairground game, otherwise feel free to improvise with what you have at hand.

A net or bowl to scoop objects out of the bath could work well – the important thing is for your child to be having fun and looking at numbers. You could allocate prizes to certain numbers if you want to.

Sidewalk chalk is brilliant for larger-scale mark-making and games that get children using their gross motor skills.

Use sidewalk chalk to write out large numerals, then give your child a paintbrush and a pot of water and have them paint over the numerals with water to erase them.

Not only does this help your child to recognise numerals but also helps with the beginnings of formation.

Create a chart using beads and pipe cleaners. Attach 10 pipe cleaners to a piece of card and write numbers 1-10, one number above each pipe cleaner. Provide your child with a pot of beads and help them to count out the correct number onto each pipe cleaner.

This activity gives your child the opportunity to practice numeral recognition, counting, and assigning the correct value to each numeral. It’s also brilliant for their fine motor skills!

Label some buckets or baskets with numbers and provide your child with beanbags. Have your child step back from the buckets and take aim and throw the bean bags in.

You can do quite a lot with this activity depending on your child’s age, stage and needs, but on the most basic level, it encourages number recognition along with introducing the concept of more and less.

If your child is ready then you can model addition and play to win.

Label pots with numerals and provide counters, craft beads, pom poms or really whatever you have at hand and encourage your child to fill each pot with the correct number of items.

Again, this activity targets a variety of different skills as children recognise numerals, apply their understanding of value, and count out the correct number of items. Another good one for fine motor skills!

Children love to learn outdoors and on a large scale. Many teachers love using small number lines in the classroom to introduce the ideas of one more and one less but you can do the same outside.

Perhaps use chalk to draw out your number line and encourage your child to locate different numerals – “Stand on number 8,” “Hop to number 4” and so on.

If appropriate you could discuss one more and one less. You could also use the number line to encourage counting by inviting your child to find 1 item to place next to the number 1, 2 items to place next to the number 2 and so on.

If your child likes to be creative and artistic then this could work for her. Use nature to create the shapes of numbers.

This might mean drawing in the mud or sand, arranging leaves or stones or even noticing natural shapes in the environment. You could do this in your backyard or take a special walk.

Even better if you can take photos of your creations for your child to look back on. This allows your child to begin thinking about how numerals are formed in a fun and creative way.

Hopscotch is a real playground classic and it brings together a whole host of skills including gross motor skills.

Draw out a hopscotch grid and teach your child how to play, throwing a stone or stick to find out where he needs to hop to, and then hopping and jumping to the end.

As well as reinforcing the recognition of numerals this also introduces the idea of higher and lower and allows your child to have fun while working with numbers.

Hopscotch is my favourite number activity for preschool kids!

11. Potion Recipes

If you like messy, creative play then this one’s for you!

Create a couple of ‘recipe cards’ using measurements expressed as numerals, for example – 2 cups of water, 3 pinecones and have your child follow the recipe card, combining everything together in a big cauldron-like tub.

This taps into children’s imaginations and introduces the concept of measurement as well as number. Once your child is finished following the recipes you have provided perhaps he will be ready to create his own recipes, which you can scribe for him.

All you need is a nice big roll of paper with numbers on and a fly swat dipped in paint. You call out the numbers and your child must swat them, thereby covering them in paint! This is a really fun preschool number activity.

You can play just as easily without the paint, simply swatting at the numerals, but it’s far less fun than making a mess. 

This activity is extremely physical helping to really embed the learning, and as your child tries to speed up, her ability to recognise numerals will improve too so that she’ll soon be able to recognise them at a glance.

Bingo is a great maths game for building up number awareness and can be enjoyed as a family. To start off with you can simply use numerals up to ten but as your child’s knowledge expands so can your game.

You can use what you have on hand – a bowl and folded up pieces of paper, with highlighters – or you can go ahead and buy bingo pads and dabbers and bingo balls to add to the overall experience.

Here you will be building number recognition and as your child aims to increase their speed, she will get quicker and quicker at recognising numbers and linking them to the number names being called out!

I hope you’ll enjoy trying out these number recognition games with your preschooler! Here are some more fun math activities for preschoolers to build early mathematical skills.

Get FREE access to Printable Puzzles, Stories, Activity Packs and more!

Join Empowered Parents + and you’ll receive a downloadable set of printable puzzles, games and short stories, as well as the Learning Through Play Activity Pack which includes an entire year of activities for 3 to 6-year-olds.
Access is free forever.

Signing up for a free Grow account is fast and easy and will allow you to bookmark articles to read later, on this website as well as many websites worldwide that use Grow.

• Share
• Email

Development of numerical literacy of children in preschool institutions

Arthur J. Baroody, PhD
College of Education, University of Illinois at Urbana-Champaign, USA
July 2010 (English). Translation: June 2015

Introduction

There has been a long discussion about how best to help children learn how to perform addition and subtraction with elementary numbers (for example, 3+4=7 and 9+5=14; 7–3=4 and 14– 9=5) (see Baroody & Dowker ¹ , especially chapters 2, 3, 6 and 7). However, scientists agree that children need to achieve a certain level of fluency in elementary calculations ² . Such fluency implies the efficient (fast and accurate) calculation of the sum and difference in examples, as well as the correct and flexible application of this knowledge. Over the past 40 years, it has become obvious that everyday (informal) mathematical knowledge of children is the basis for learning (formal) mathematics at school ^3,4,5 . For example, studies show that developing children's sense of numbers contributes to fact fluency ^6,7,8,9 . The purpose of this article is to summarize the data on how the development of ordinary number sense before the first grade of school provides the basis for the formal skill of fluency in elementary calculus, which is key in the primary grades.

Key Questions

1. When should parents and preschool teachers begin to (a) help develop a child's sense of numbers and (b) directly develop children's fluency in elementary calculus?
2. What age prerequisites should children have initially in order to quickly and effectively achieve fluency in elementary calculations?
3. What role does language play in the development of this basic knowledge?
4. How can parents and preschool teachers best encourage the development of a sense of number and fluency in elementary calculus?

Recent Research Results

Question 1. Helping children develop their sense of numbers - the basis of fluency in elementary calculations - can and should begin as early as preschool age. Recent research shows that children begin to develop a sense of number very early. In fact, toddlers as young as 18 months and almost all children as young as two years of age already have the initial inclinations required for fluency in elementary calculus (see review by Baroody, Lai & Mix ³ ).

The effectiveness of efforts aimed at increasing fluency in elementary calculations depends on whether the child is ready for learning in terms of age, and on the pace of learning offered to him. As recent studies show, significant individual differences in number sense appear as early as 2-3 years of age and often increase with age ^3.10 , as a result of which there are no strict prescriptions for when to begin the systematic development of fluency in calculations. Of course, for many children, due to the peculiarities of their development, this teaching of even the simplest calculations (n ​​+ 0 and n + 1) should begin no earlier than the last year of kindergarten or the first grade of school ¹¹ . For children who are predicted to have a high probability of academic failure, problems with elementary numbers most likely do not make sense to offer up to the first or second grade of school ¹² . Questions 2 and 3 ¹³ ). More specifically, language provides the foundation for two basic components of early childhood number sense, namely the notion of the cardinal number of the set (the total number of elements in the set) and the capacity for verbal number recognition, VNR, sometimes called "verbal subitization", which is noted at the top of Figure 1 . TCG means accurately and quickly determining the number of elements in small sets and naming them with the appropriate numeral. The use of the words "one", "two", "three" in combination with the demonstration of relevant and irrelevant examples can help children 2-3 years old develop an accurate and reliable "intuitive understanding" of numbers one, two, three - understanding when something is one, something two, something three.

• By seeing pictures of ●●, ∆∆, and o o (relevant examples of pairs) and hearing them denoted by the numeral "two", children can understand that the appearance of the elements of a set is not important (shape and color do not affect the quantity). Also, as a result, they may have the designation "two" for the intuitive idea of the multiplicity of (there are more than one).
• By seeing pictures of ●, ●●●, ∆, ∆∆∆, , and (irrelevant examples of pairs) indicated by the words “not two” or another numeral, children can determine the boundaries of the concept two .

A key recommendation for such tasks is that the basic understanding of the cardinal number of a set is not innate and does not develop automatically during ontogeny (cf. Dehaene ¹⁵ ) ^14.16 . Parents and preschool educators play an important role in this process as they provide the experience and feedback needed to form the concept of number. Therefore, they should use everyday situations to indicate small sets and encourage children to do the same (for example, “How many feet do you have?” - “So you need two shoes, not one” or “You can take one cookie, but not two "). Some children start going to kindergarten before they have learned to distinguish all the "intuitive" numbers. Such children are at serious risk of being among the underachievers in school and need intensive remedial classes. When diagnosing the abilities of kindergarten students, it should be checked whether children can quickly distinguish sets of one, two and three items and distinguish them from somewhat larger sets of four and five items.

As shown in Figure 1 , the interrelated development of the cardinal concepts of intuitive numbers and the ability to verbally recognize numbers can provide the foundation for a wide range of numerical, counting, and arithmetic concepts and skills. These skills can provide the basis for meaningful verbal counting. Recognizing "intuitive" numbers can help children see visually that the group labeled "two" includes more items than the group labeled "one" and that the group "three" includes more items than the group "two". This basic understanding of ordinal numbers will in turn help children understand that the order of numbers is important when counting ( the principle of ownership of the number series ), and that the sequence of numbers (“one, two, three ...”) reflects the increase in the number of elements in the set. Once the child masters the sequence of counting words, he develops the ability to start counting from any number and (correctly) call the next number in the sequence ( skill of determining the next number ) without starting again from one.

The ability to automatically name the next number in a counting sequence can be the basis for realizing that adding one to any number creates a larger number and, further, for mastering this operation when rearranging the terms in the examples n + 1 / 1 + n. When one is added to a number, the sum is the next number in the counting sequence (for example, the sum for 7+1 is the next number after seven, or eight). This reasoning strategy will help children calculate sums in similar combinations if they know the counting sequence, including even multi-digit numbers such as 28+1, 128+1 or 1000128+1. Over time, this reasoning strategy becomes automatic; can be effectively applied without thought (becomes a component of the playback/retrieval system). In other words, it becomes the basis for fluency in solving n+1 / 1+n combinations.

TCG and an understanding of the order of counting that it includes can form the basis for a meaningful counting of objects ¹⁷ . Children who can distinguish between "one", "two", and "three" learn to count objects more easily with the help of adults than children who cannot distinguish between these numbers. They also have a better understanding of the purpose of counting (one way to determine the total number of items) and the reasons for certain actions in the counting process (for example, someone repeats the last word in a count to emphasize that this is the total number of items). Meaningful counting of objects is needed to develop counting strategies (using objects or numbers) in order to determine sums and differences. Once these strategies are established, attention shifts to the exploration of orders and relationships; these mathematical patterns, in turn, serve as the basis for reasoning strategies (that is, how the child will solve an unfamiliar example using the examples and relationships known to him). Once these reasoning strategies become automatic, they can serve as one strategy for efficiently retrieving responses from memory.

TCG allows the child to see the combination "one+one" as "two", "one+one+one" as "three" and vice versa (for example, "three" as "one+one+one"). Thus, the child constructs an understanding of combination and decomposition (the whole can be made up of several parts or broken into parts in different ways). If a child constantly sees before him examples of the combination and decomposition of "two" and "three", this will lead to the development of fluency in calculations of elementary sums and differences ("one plus one equals two", "two plus one equals three" and "two minus one equals one"). Decomposing "four" and "five" into parts with feedback (for example, a child calls a group of four objects "two plus two", and another person confirms: "Yes, two plus two is four") can lead to fluency in elementary calculations. sums up to five and using the "next number rule" in n+1/1+n combinations (as discussed earlier).

The concept of cardinality, CCG, and the concepts of addition and decomposition into components provide the basis for the formation of the concepts of addition and subtraction. For example, adding one object to a group of two objects, the child clearly sees that the original group is transformed into a larger group and already consists of three objects. Such competencies, in turn, serve as the basis for the formation of a concrete-abstract understanding of the following arithmetic concepts ¹⁸ :

• The concept of subtraction to zero (subtractive negation). For example, children realize that if two blocks are removed from two available blocks, then nothing remains. This realization can develop into a generalization that if you subtract it from any number, then nothing remains.
• The concept of quantity immutability (additive and subtractive identity). For example, when children understand that if two dice are subtracted from zero, then two dice remain, they can develop a generalization that subtracting zero from any number will leave that number unchanged.

Both concepts serve as the basis for the development of fluency in elementary calculations of examples of type n – n = 0 and type n – 0 = n.

A poorly developed sense of numbers can interfere with the achievement of fluency in elementary calculations and the achievement of success in mathematics. For example, Mazzocco & Thompson ¹⁹ found that the performance of preschoolers on four types of items from the Test of Early Mathematics Ability – Second Edition; learning mathematics in the second and third grades. These tasks include the following: meaningful object counting (with the knowledge that the last number is the number of objects), the concept of cardinality, comparing single-digit numbers (for example, “Which is greater - four or five?”), addition of single-digit numbers in the mind and reading the corresponding numbers. It should be noted that the ability to verbally recognize "intuitive" numbers is one of the foundations for the first three skills mentioned above and a significant factor in mastering the fourth.

Question 4. In order to stimulate the formation of a sense of number in general and fluency in elementary calculations in particular, it is necessary to create opportunities for children to explore patterns and relationships. For example, a child who has learned in a meaningful way "pairs / doublings" "5 + 5 = 10", "6 + 6 = 12", etc. (for example, the child understands that all such sums are even, or divisible by two), can use this knowledge to calculate unknown sums of the “pair+1” type: for example, 5+6 (i.e. 5+(5+ 1) or (5+5)+1) or 7+6.

In order to be appropriate for a child's developmental stage, learning opportunities must be purposeful, meaningful and problem-oriented ²⁰ .

• Education should be focused and interesting for children. This can be achieved by incorporating learning moments into a structured game (for example, playing a dice game can help children learn to recognize numbers from one to six). Music and drawing can serve as natural aids to bring attention to patterns, numbers, and shapes (eg, maintaining a two- or three-clap rhythm; drawing a number of balloons). Parents and educators can use numerous daily situations to teach (for example, "How many feet do you have? ... So, how many socks do you need to get out of the drawer?"). Children's questions can be an important source of purposeful learning.
• Learning should be meaningful for children and gradually build on (and connect with) what they already know. For adults working with 2-year-olds, a significant goal is to teach children to recognize the number "two". You should not be too hasty in teaching children about subsequent numbers, such as the number "four", as this may reduce their motivation (the child may become inattentive or aggressive, give answers inappropriately, or otherwise withdraw from the activity).
• Teaching should be, as far as possible, problem-oriented or thought-provoking. Instead of just giving children some information, parents and educators should give children the opportunity to think about a problem or problem, make assumptions (thoughtful guesses), develop their strategy, or deduce their answer.

Cases of Alice ²¹ and Lucas ²² illustrate some of the aspects described above:

• Case of Alice. By the age of two and a half, Alice was already able to confidently distinguish one, two or three objects. Therefore, her parents wanted to expand the range of the girl's knowledge to the number "four", which at that time was beyond her capabilities. Instead of just saying the number "four" when describing groups of four, they asked Alice questions about such groups. The girl often answered, having previously divided the unfamiliar group into two acquaintances. Then her parents completed her answer: "Two plus two equals four." When Alice was shown a picture of four puppies at 30 months of age, she placed two fingers of her left hand on two puppies and said, "Two." Without removing her left hand, she placed two fingers of her right hand on the other two puppies and said, "Two." She then used the statement she learned from her parents that "two plus two equals four" to indicate the cardinal number of puppies in the painting.
• Case of Lucas. In the context of a computer math game, Lucas was presented with the example 6+6. He determined the amount using the account. Then he was shown an example of 7 + 7. He smiled and quickly replied, "Thirteen." When the computer announced the correct answer, the number 14, Lucas looked puzzled. After a couple of tasks, he got an example of 8 + 8, and Lucas explained: “I was going to answer 15, because 7 + 7 was 14. But before that, 6 + 6 was 12, and I thought that 7 + 7 is probably 13, but was 14. So I'm going to answer that 8+8 is 16."

Future Directions

Much remains to be learned about the development of math skills in preschoolers. Does Verbal Number Recognition at Age Two Affect Kindergarten Readiness and Math Performance in School? If so, can an intervention based on relevant and irrelevant examples help children at risk of achievement to catch up with their peers? What other well-formed concepts or skills can predict kindergarten readiness or school math performance in two- to three-year-olds? How effective are the programs currently being developed for early mathematical development?

Conclusions

Contrary to the opinion of many preschool teachers, teaching mathematics to children at the age of two makes sense ^23,24,25,26 . As shown in Figure 1, this training should begin with the development of children's understanding of "intuitive" cardinal numbers, as well as the skill of recognizing and labeling groups of one to three objects with the corresponding numerals. As shown in Figure 1, this knowledge of numbers is key to the subsequent development of numeracy, and children with math difficulties may often lack it ²⁷ . Early learning does not mean that preschoolers will be bombarded with a huge amount of information and forced to practice with flashcards and memorize arithmetic examples. In order to develop children's sense of numbers and fluency in elementary calculations, help children identify relationships and patterns, and encourage them to invent their own reasoning strategies.

Figure 1. Learning trajectories for some key numerical, counting and arithmetic concepts and skills

The studies described were supported by a grant from the National Science Foundation (BCS-0111829), the Spencer Foundation (mega-grant 200400033), the National Institutes of Health (1 R01 HD051538-01), and the Institute of Education and Science (R305K050082) . The views expressed in this manuscript solely reflect those of the author and do not necessarily reflect the position, policy, or endorsement of the aforementioned institutions.

Literature

1. Baroody AJ, Dowker A. The development of arithmetic concepts and skills: Constructing adaptive expertise. In: Schoenfeld A, ed. Studies in mathematics thinking and learning series . Mahwah, NJ: Lawrence Erlbaum Associates; 2003.
2. Kilpatrick J, Swafford J, Findell B, eds. Adding it up: Helping children learn mathematic s. Washington, DC: National Academy Press; 2001.
3. Baroody AJ, Lai ML, Mix KS. The development of number and operation sense in early childhood. In: Saracho O, Spodek B, eds. Handbook of research on the education of young children . Mahwah, NJ: Erlbaum; 2006: 187-221.
4. Clements D, Sarama J, DiBiase AM, eds. Engaging young children in mathematics: Standards for early childhood mathematics education . Mahwah, NJ: Lawrence Erlbaum Associates; 2004: 149-172.
5. Ginsburg HP, Klein A, Starkey P. The development of children’s mathematical knowledge: Connecting research with practice. In: Sigel IE, Renninger KA, eds. Child psychology in practice . 5th Ed. New York, NY: Wiley & Sons; 1998; 401–476. Handbook of child psychology , vol 4.
6. Baroody AJ. Why children have difficulties mastering the basic number facts and how to help them. Teaching Children Mathematics 2006;13:22–31.
7. Baroody AJ, Thompson B, Eiland M. Fostering the fact fluency of grade 1 at-risk children. Paper presented at: The annual meeting of the American Educational Research Association. April, 2008. New York, NY.
8. Gersten R, Chard, D. Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. The Journal of Special Education 1999;33(1):18–28.
9. Jordan NC. The need for number sense. Educational Leadership 2007;65(2):63–66.
10. Dowker AD. Individual differences in arithmetic: Implications for psychology, neuroscience and education . Hove, England: Psychology Press; 2005.
11. Baroody AJ. The development of kindergartners' mental-addition strategies. Learning and Individual Differences 1992;4:215-235.
12. Baroody AJ, Eiland M, Thompson B. Fostering at-risk preschoolers' number sense. Early Education and Development 2009;20:80-120.
13. Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal processes in early quantitative development. In: Kail R, ed. Advances in child development and behavior , vol 33. New York, NY: Academic Press; 2005: 305-346.
14. Baroody AJ, Li X, Lai ML. Toddlers' spontaneous attention to number. Mathematics Thinking and Learning 2008;10:1-31.
15. Dehaene S. The number sense . New York, NY: Oxford University Press; 1997.
16. Wynn K. Numerical competence in infants. In; Donlan C, ed. Development of mathematical skills . Hove, England: Psychology Press; 1998: 1-25.
17. Benoit L, Lehalle H, Jouen F. Do young children acquire number words through subitizing or counting? Cognitive Development 2004;19:291–307.
18. Baroody AJ, Lai ML, Li X, Baroody AE. Preschoolers' understanding of subtraction-related principles. Mathematics Thinking and Learning 2009;11:41–60.
19. Mazzocco M, Thompson R. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice 2005;20:142-155.
20. Baroody AJ, Coslick RT. Fostering children's mathematical power: An investigative approach to K-8 mathematics instruction . Mahwah, NJ: Erlbaum; 1998.
21. Baroody AJ, Rosu L. Adaptive expertise with basic addition and subtraction combinations: The number sense view. In: Baroody AJ, Torbeyns T. chairs. Developing Adaptive Expertise in Elementary School Arithmetic. Symposium held at: The annual meeting of the American Educational Research Association. April, 2006. San Francisco, CA.
22. Baroody AJ. Fostering early number sense. Keynote address at: The Banff International Conference on Behavioral Science. March, 2008. Banff, Alberta.
23. Baroody AJ, Li X. Mathematics instruction that makes sense for 2 to 5 year olds. In: Essa EA, Burnham MM, eds. Development and education: Research reviews from young children . New York: The National Association for the Education of Young Children; 2009: 119-135.
24. Bredekamp S, Copple C. Developmentally appropriate practice in early childhood programs. Washington, DC: National Association for the Education of Young Children; 1997.
25. Copley J, ed. Mathematics in the early years, birth to five . Reston, VA: National Council of Teachers of Mathematics; 1999.
26. Copley J, ed. The young child and mathematics. Washington, DC: National Association for the Education of Young Children; 2000.
27. Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8-9 year old students. Cognition 2004;93:99–125.

This article was originally published in the Encyclopedia of Language Development and Literacy by the University of Western Ontario, who owns the copyright to this article.

Numerical knowledge in early childhood

Katherine Sophian, PhD
University of Hawaii, USA
June 2009 (English). Translation: June 2015

Introduction

In recent years, there has been a dramatic increase in research on the knowledge of numbers in young children. The focus of these studies is a wide variety of abilities and ideas, ranging from the ability of infants to distinguish between groups containing a different number of objects ^1.2 , to understanding by preschoolers of numerals (words denoting numbers) ^3.4 and counting ^{5.6, 7} , as well as inverse relations between addition and subtraction ^8.9 .

Subject

The study of young children's knowledge of numbers lays the foundation for setting standards for preschool education ¹⁰ and for developing a work program in mathematics for preschoolers ^11,12,13 . In addition, mathematical knowledge acquired at preschool age influences further school performance and career choice in the future ¹⁴ . An analysis of school performance predictors based on data from six longitudinal studies found that children's math skills at school entry were more predictive of later school performance than were reading skills, attention span, or socio-emotional skills ¹⁵ .

Issues

Numerical literacy is basically about understanding that numbers represent different things. Accordingly, studying how number literacy develops in early childhood leads to an understanding of how children come to understand the basic quantitative relationships that numbers and other types of quantities have in common, as well as the properties of numbers that distinguish them from other types of quantities.

Scientific context

Piaget's classic study of logico-mathematical development examined how children understand the general properties of quantities, such as seriation and the preservation of equivalence relations under certain kinds of transformations ¹⁶ . However, J. Piaget believed that this kind of knowledge appears with the development of concrete-operational thinking in children at the age of 5-7 years. Subsequent research ¹⁷ showed that young children have more numerical knowledge than Piaget admitted; and modern research indicates that babies have a wide range of abilities to operate with the numbers ¹⁸ .

Key Questions

According to the authoritative though controversial view presented in the modern literature on early number abilities, the brain is "hard-wired" for the number ^19.20 . In support of this idea, the ability babies and animals distinguish between the number of objects ²¹ . However, critics of nativist views on numerical knowledge (the philosophical doctrine that the brain is born with ideas/knowledge) note that mathematical thinking undergoes continuous changes in the course of development, that the concept of number is slowly differentiated from other quantitative dimensions ^22.23 , and numerical knowledge that appears at an early age is contextually determined ²⁴ . Moreover, accumulated evidence suggests that language ²⁴ and other cultural products and practices ^25.26 make a huge contribution to the acquisition of numerical knowledge by young children.

Recent research results

Numerical knowledge in infancy

One of the most rapidly developing areas of modern research is devoted to the ability of infants to operate with numbers. Kobayashi, Hiraki and Hasegawa ¹ used the discrepancy between visual and auditory information about the number of objects in a group in order to assess the ability of six-month-old children to distinguish between quantities. They showed babies objects that made a sound when they hit the surface, then dropped two or three objects behind the screen so that the babies heard the sound of each falling, but did not see the objects themselves. After that, they removed the screen, and the correct or incorrect number of objects was revealed to the gaze (3 if there were 2 impact sounds, and vice versa). Infants stared longer when the number of objects did not match the number of sounds they heard, suggesting that they were able to distinguish two objects from three. Other studies show that six-month-olds are able to pick up quantitative differences between more items, as long as they are significant. Six-month-old babies distinguish 4 from 8 ²⁷ and even 16 from 32 ²⁸ . However, if the difference is reduced (for example, 8 and 12), six-month-old babies are wrong ²⁹ , and older children are more successful ² . Thus, with age, infants develop the ability to distinguish between quantities more accurately.

Young children's knowledge of number relationships

Since numbers represent a quantity, basic knowledge about numbers is related to understanding that numerical quantities enter into equal and greater/less than relationships ³⁰ . Research on infants reveals a surprising fact: for preschoolers, an important developmental achievement is their ability to compare groups of objects numerically, especially when this entails the ability to ignore other differing features.

For example, K. Mix ³¹ studied the ability of three-year-old children to quantify sets of 2, 3, or 4 black dots. The task was completed with ease when the objects that the children had to match with the dots looked like them (for example, black disks or red shells about the same size as the dots). However, the success of the task fell when the objects differed from the points in shape (for example, figurines of lions or objects of different appearance).

Muldoon, Lewis and Francis ⁷ studied the ability of four-year-old children to evaluate the numerical ratio of two rows of blocks (with 6-9 blocks per row) in conditions where the length of the rows is deliberately misleading, i.e. when two rows of different length contain the same number of elements or two rows of the same length contain a different number of elements. Most of the children relied on row length comparisons rather than element counts. However, after three training sessions, the results improved, especially in those children who were asked during the training to explain why the rows are equal or unequal numerically (the fact that the rows are equal or unequal, they were informed by the experimenter).

Unexplored areas

While experimental data on early childhood numeracy is growing exponentially, the lack of a general theory that unifies the full spectrum of empirical findings limits our understanding of how the various data already collected fit together. with each other, and what questions still remain unanswered. In the literature on infancy, for example, competing hypotheses have formed the basis of numerous studies in recent years, but their results have not smoothed out the existing theoretical contradictions. When putting forward theoretical propositions, scientists must be aware of the results of all other studies, and their theories must be formulated so precisely as to allow empirical testing.

In addition, researchers need more information about the processes that lead to the development of number understanding at an early age. We know that many environmental factors affect the performance of young children, ranging from culture and social class ³² to parent-child relationship patterns ^33.34 and teacher-child relationship ³⁵ . At the moment, science has little information in terms of volume, mainly from experimental studies with training ^7,25,36 , about how a particular experience changes children's numerical thinking. Particularly useful would be those studies that provide summary data on (a) children's daily experiences with numbers and how these experiences change with age, and (b) the experimental impact of such experiences on a child's thinking.

Conclusions

The available research on how number knowledge develops in childhood supports four general conclusions that are of great importance for practice and administrative directives. First, the development of knowledge about numbers is multifaceted. Numerical literacy in early childhood is much more than just counting and basic arithmetic. Second, despite the evidence that infants already have the ability to recognize numbers, age-related changes are continuous. When comparing children of different ages, older children almost always perform better. Thirdly, variability is also ubiquitous. All children deal with different problems with numbers 9 in different ways.0014 37 , resort to different arguments when operating with numbers in various situations ³ and even give different answers when performing the same task in different attempts ^{5. 38} . And, finally, the progress of children in the development of numerical knowledge is very susceptible to external influences. The success of the development of children's numerical knowledge is influenced by non-learning activities, such as board games ²⁵ , specially organized, experimental activities aimed at explaining numerical relationships to children ^7.36 , as well as the forms and ways in which parents ^33.34 and teachers ³⁵ tell children about numbers.

Recommendations

An important contribution of early childhood numeracy research to practice and administrative guidelines is that its results can help to adjust the goals that are set for teaching preschoolers mathematics. Since the development of numeric knowledge in early childhood is multifaceted, the goals for educational programs should be much broader than simply teaching children numeracy and basic arithmetic. Numbers, like other quantities, are characterized by relations of equality and inequality. At the same time, numbers differ from other quantities in that they are based on the division of the total number into elements. Learning activities that encourage children to think about the relationships between quantities and how those quantities are affected by transformations such as division, grouping, or regrouping can speed up children's learning of these concepts. Due to the diversity and plasticity of young children's numerical thinking, curricula at this stage have great potential to increase children's knowledge of numbers.

Literature

1. Kobayashi T, Hiraki K, Hasegawa T. Auditory-visual intermodal matching of small numerosities in 6-month-old infants. Developmental Science 2005;8(5):409-419.
2. Xu F, Arriaga R.I. Number discrimination in 10-month-olds. British Journal of Developmental Psychology 2007;25(1):103-108.
3. Mix KS. How Spencer made number: First uses of the number words. Journal of Experimental Child Psychology 2009;102(4):427-444.
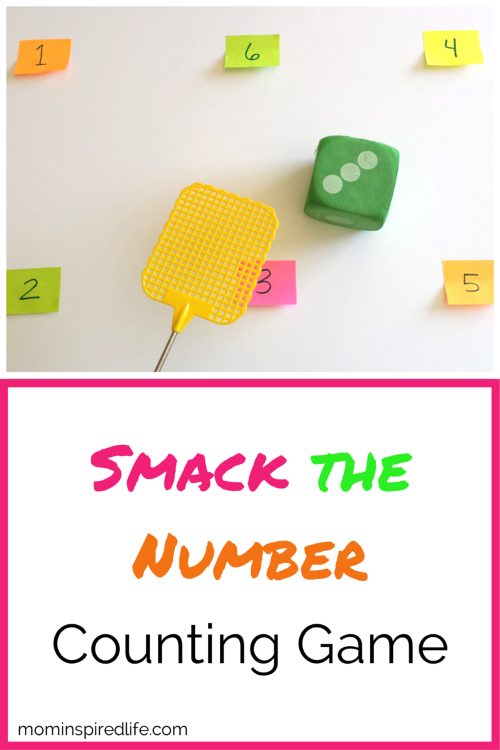
4. Sarnecka BW, Lee MD. Levels of number knowledge in early childhood. Journal of Experimental Child Psychology 2009;103(3):325-337.
5. Chetland E, Fluck M. Children’s performance on the ‘give-x’ task: A microgenetic analysis of ‘counting’ and ‘grabbing’ behavior. Infant and Child Development 2007;16(1):35-51.
6. Le Corre M, Carey S. One, two, three, four, nothing more: an investigation of the conceptual sources of the verbal counting principles. Cognition 2007:105(2):395-438.
9002 K, C, Francis B Francis B. Developmental Science 2007;10(5):694-711.
7. Canobi KH, Bethune NE. Number words in young children's conceptual and procedural knowledge of addition, subtraction and inversion. Cognition 2008;108(3):675-686.
8. Sherman J, Bisanz J. Evidence for use of mathematical inversion by three-year-old children. Journal of Cognition and Development 2007;8(3):333-344.
9. Clements DH, Sarama J, DiBiase AM, eds. Engaging young children in mathematics: Standards for early childhood mathematics education . Mahwah, N.J.: Lawrence Erlbaum Associates; 2004.
10. Clements DH, Sarama J. Experimental evaluation of the effects of a research-based preschool mathematics curriculum. American Educational Research Journal 2008; 45(2):443-494.
11. Griffin S, Case R. Re-thinking the primary school math curriculum: An approach based on cognitive science. Issues in Education 1997;3(1):1–49.
12. Starkey P, Klein A, Wakeley A. Enhancing young children’s mathematical knowledge through a pre-kindergarten mathematics intervention. Early Childhood Research Quarterly 2004;19(1):99-120.
13. National Mathematics Advisory Panel. Foundations for success: The final report of the National Mathematics Advisory Panel . Washington, DC: U. S. Department of Education; 2008.
14. Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, Pagani LS, Feinstein L, Engel M, Brooks-Gunn J, Sexton H, Duckworth K, Japel C. School readiness and later achievement. Developmental Psychology . 2007;43(6):1428-46.
15. Piaget J. The child's conception of number . Gattegno C, Hodgson FM, trans. New York, NY: Norton; 1952.
16. Gelman R, Gallistel CR. The child's understanding of number . Cambridge, MA: Harvard University Press; 1978.
17. Geary DC. Development of mathematical understanding. In: Damon W, ed. Handbook of child psychology. 6th ed. New York, NY: John Wiley & Sons; 2006:777-810. Khun D, ​​Siegler RS ​​Siegler, eds. Cognition, perception, and language .Vol. 2.
18. Butterworth B. The mathematical brain . New York, NY: Macmillan; 1999.
19. Dehaene S. The number sense: How the mind creates mathematics . Oxford, UK: Oxford University Press; 1997
20. Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences 2004;8(3):307-314.
21. Sophian C. Beyond competence: The significance of performance for conceptual development. Cognitive Development 1997;12(3):281-303.
22. Sophian C. The origins of mathematical knowledge in childhood . New York, NY: Lawrence Erlbaum Associates; 2007.
23. Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal quantification in early childhood. In: RV Kail, ed. Advances in child development and behavior .vol. 33. New York, NY: Academic Press; 2005:305-346.
24. Ramani GB, Siegler RS. Promoting broad and stable improvements in low-income children's numerical knowledge through playing number board games. Child Development 2008;79(2):375-394.
25. Schliemann AD, Carraher DW. The evolution of mathematical reasoning: Everyday versus idealized understandings. Developmental Review 2002;22(2):242-266.
26. Xu F. Numerosity discrimination in infants: Evidence for two systems of representation. Cognition 2003;89(1):B15-B25
27. Xu F, Spelke ES, Goddard S. Number sense in human infants. Developmental Science 2005;8(1):88-101.
28. Xu F, Spelke ES. Large-number discrimination in 6-month-old infants. Cognition 2000;74(1):B1-B11.
29. Davydov V.V. Logical and psychological problems of elementary mathematics as an academic subject. In: Kilpatrick J, Wirszup I, Begle EG, Wilson JW, eds. Soviet studies in the psychology of learning and teaching mathematics .Chicago, Ill: University of Chicago Press; 1975: 55-107. Steffe LP, ed. Children's capacity for learning mathematics. Vol. 7.
30. Mix KS. Surface similarity and label knowledge impact early numerical comparisons. British Journal of Developmental Psychology 2008;26(1):1-11.
31. Starkey P, Klein A. Sociocultural influences on young children’s mathematical knowledge. In: Saracho ON, Spodek B, eds. Contemporary perspectives on mathematics in early childhood education . Charlotte, NC: IAP/Information Age Pub. ; 2008:253-276.
32. Blevins-Knabe B, Musun-Miller L. Number use at home by children and their parents and its relationship to early mathematical performance. Early Development and Parenting 1996;5(1):35-45.
33. Lefevre J, Clarke T, Stringer AP. Influences of language and parental involvement on the development of counting skills: Comparisons of French- and English-speaking Canadian children. Early Child Development and Care 2002;172(3):283–300.
34. Klibanoff RS, Levine SC, Huttenlocher J, Vasilyeva M, Hedges LV. Preschool children's mathematical knowledge: The effect of teacher "math talk." Developmental Psychology 2006;42(1):59-69.
9002 C, Gartes D, C. Developmental Psychology 1997;33(5):731-744.
35. Dowker A. Individual differences in numerical abilities in preschoolers. Developmental Science 2008;11(5):650-654.
36. Siegler RS. How does change occur: A microgenetic study of number conservation.

    ---

    Learn more

    • 
      The opposite game
    • 
      Game for preschool children
    • 
      Simple rhyming words
    • 
      Alphabet preschool songs
    • 
      Write letter c
    • 
      Three small pigs story
    • 
      Space story for preschool
    • 
      Preschool reading skills
    • 
      Kids ii logo
    • 
      Writing skill for kids
    • 
      3 little pigs and the big bad wolf story