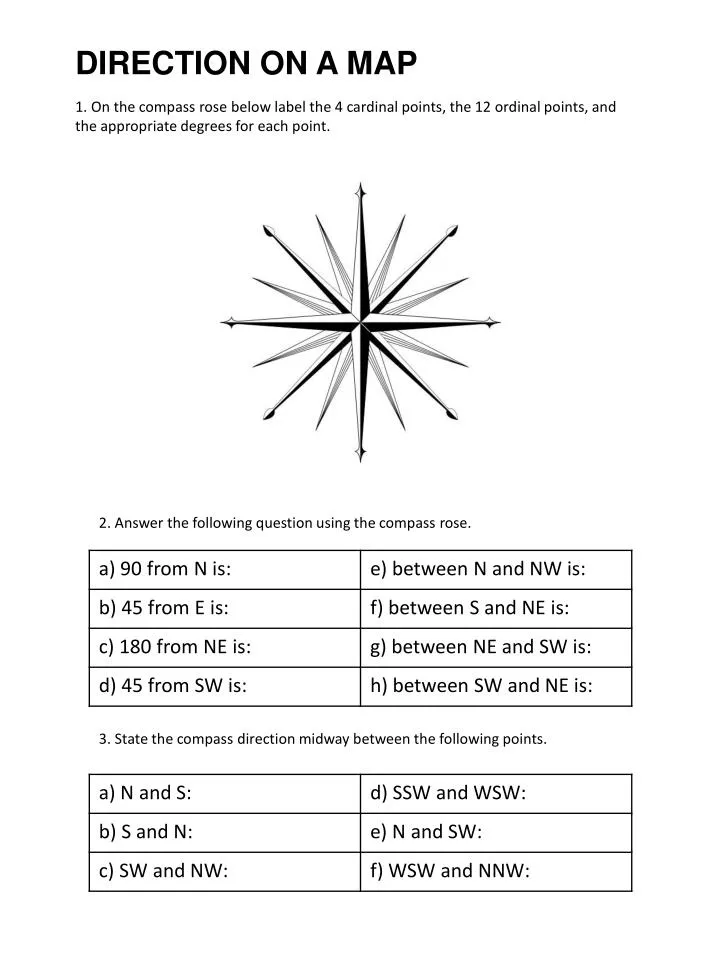
Cardinal math definition
Cardinal Numbers - Meaning, Examples, Sets
Cardinal numbers are numbers that are used for counting. They are also known as natural numbers or cardinals. A set of cardinal numbers starts from 1 and it goes on up to infinity. We use cardinal numbers to answer the question "how many?". For example, how many students are going to the school picnic? The answer could be any number like 20, 23, 30, etc. So, all these numbers come in the category of cardinal numbers. In this article, we will explore the world of cardinal numbers and understand the difference between cardinal and ordinal numbers.
| 1. | What are Cardinal Numbers? |
| 2. | Difference Between Cardinal and Ordinal Numbers |
| 3. | List of Cardinal Numbers from 1 to 100 |
| 4. | Cardinal Numbers of a Set |
| 5. | FAQs on Cardinal Numbers |
What are Cardinal Numbers?
A cardinal number describes or represents how many of something are present. Example 2 apples, 5 flowers, etc. It quantifies an object. It does not have values as fractions or decimals. Cardinal numbers are counting numbers, they help to count the number of items. Let's have a look at cardinal numbers examples. Ana wants to count the number of people standing in a queue at a billing counter. Can you help her? Ana started to count using Natural numbers.
Ana counted 1, 2, 3, 4, and 5. There are 5 people standing in a queue at the billing counter. Counting numbers are cardinal numbers! Now, Let's consider another example, Noah kept eight apples in a basket. The number eight denotes how many apples are there in the basket, irrespective of their order.
Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on. The smallest cardinal number is 1 as 0 is not used for counting, so it is not a cardinal number.
Difference Between Cardinal and Ordinal Numbers
All the natural numbers are also referred to as cardinal numbers.
Cardinal numbers are used for counting. While an ordinal number is a number that denotes the position or place of an object. Example: 1st, 2nd, 3rd, 4th, 5th, etc. Ordinal numbers are used for ranking. Here is an example that explains cardinal and ordinal numbers:
In the above image, we can see a team of 4 workers on the construction site. This is an example of cardinal numbers.
In the above image, we can see the position of the runners in the running event. First, second, third, and so on. This is an example of ordinal numbers. Let's discuss ordinal and cardinal number differences in the table below:
| Cardinal Numbers | Ordinal Numbers |
|---|---|
| They are counting numbers that represent quantity. | They are based on the rank or position of an object in a given list or order. |
Cardinal numbers give us the answer of 'how many?'. |
Ordinal numbers give us the answer of 'where'. For instance, where does the object lies in the list? |
| Examples are 1, 2, 3, 4, 5, 10, etc. | Examples are 1st, 2nd, 3rd, 4th, 5th, 10th, etc. |
List of Cardinal Numbers from 1 to 100
Given below are the basic and most important cardinal numbers, which form the base for other counting numbers.
| 1 - One | 6 - Six |
| 2 - Two | 7 - Seven |
| 3 - Three | 8 - Eight |
| 4 - Four | 9 - Nine |
| 5 - Five | 10 - Ten |
| 10 - Ten | 60 - Sixty |
| 20 - Twenty | 70 - Seventy |
| 30 - Thirty | 80 - Eighty |
| 40 - Forty | 90 - Ninety |
| 50 - Fifty | 100 - Hundred |
Given below is the list of all cardinal numbers from 1 to 100.
It will also help you to see how we write cardinal numbers in words like 21- twenty-one.
Cardinal Numbers of a Set
In the case of a set, the cardinal number is the total number of elements present in it. In other words, the number of distinct elements present in a set is the cardinal number of the set. The cardinal number of a set A is represented as n(A). For example, the cardinal number of set W = {1, 3, 5, 7, 9} is n(W)=5, as there are 5 elements in it.
Think Tank:
- Maria wrote January 1, 2020, as today’s date in her notebook. Does the number 1 in the date, represent a cardinal number?
- There are _______ people in the line ahead of me. I am the 7th person in the line.
Important Notes:
- Cardinal numbers help us to count the number of things or people in or around a place or a group.
- The collection of all the ordinal numbers can be denoted by the cardinal.
- Cardinal numbers can be written as words such as one, two, three, etc.
- Cardinal numbers tell how many items, whereas ordinal numbers show position or ranking.
Related Articles
Check out these interesting articles to know more about cardinal numbers and its related articles.
- Ordinal Numbers
- Whole Numbers
- Natural Numbers
- Difference Between Natural and Whole Numbers
Cardinal Numbers Examples
-
Example 1: Kate has a list of numbers as shown - 7, 8th, 10, Two, Fourth, 2nd. Identify the cardinal numbers.
Solution:
7, 10 and two help us in counting, whereas 8th, fourth and 2nd helps us in identifying the position. Thus, 7, 10, and two are cardinal numbers.
-
Example 2: Help Ryan, to calculate the number of vowels in "NUMBERS".
Also, identify the number of alphabets used to form this word.Solution:
(i) We know that a, e, i, o, and u are the vowels and in the given word u and e are used. Therefore, 2 vowels are used to form this number (2 is the required cardinal number).
(ii) We start counting from N to S, we see that "Numbers" has 7 alphabets in all. Therefore, a total of 7 alphabets are required to form the given word and here 7 is a cardinal number.
go to slidego to slide
Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations with Cuemath.
Book a Free Trial Class
Practice Questions on Cardinal Numbers
go to slidego to slidego to slide
FAQs on Cardinal Numbers
What is a Cardinal Number Example?
Cardinal numbers are used for counting. Some examples of cardinal numbers are 1, 2, 3, 4, 5, 10, 15, 20, 30, 40, 50, 100, etc.
In our daily life, we use cardinal numbers a lot. Even a small child uses this mathematical concept without knowing the term for it. They do count how many toys they have, how many people are there around them, how many friends they have, how many subjects do they study at school, etc.
What is the Smallest Cardinal Number?
The smallest cardinal number is 1 (one) as whenever we count, we always start from 1.
How do you Find Cardinal Numbers?
Cardinal numbers can be found by counting. We start by 1 and then go on as per the number sequence.
How is Cardinal Number Different from the Ordinal Number?
Cardinal numbers are numbers that represent the number of items(quantity) while ordinal numbers represent the rank or position of an item in the given list.
What is a Cardinal Number in Sets?
In set A, if there are a total of 25 elements then 25 is the cardinal number of set A represented by n(A).
Can Cardinal Numbers Negative?
No, cardinal numbers cannot be negative.
They are positive integers or natural numbers, as we always count the number of items starting from number 1, and then it goes up to infinity.
Is Zero a Cardinal Number?
No, 0 is not a cardinal number as cardinal numbers represent quantity, and 0 means nothing or no quantity.
What is the Biggest Cardinal Number?
There are infinite natural numbers. Therefore, there are as many cardinal numbers as natural numbers. There can be no generalization of the biggest natural number and so does for the biggest cardinal number.
Cardinal number Definition & Meaning
- Top Definitions
- Quiz
- Examples
- British
- Scientific
This shows grade level based on the word's complexity.
Save This Word!
This shows grade level based on the word's complexity.
noun
Also called cardinal numeral. any of the numbers that express amount, as one, two, three, etc. (distinguished from ordinal number).
Also called potency, power. Mathematics. a number or symbol analogous to the number of elements in a finite set, being identical for two sets that can be placed into one-to-one correspondence: The cardinal number of the set a1, a2, … an is n.
QUIZ
SHALL WE PLAY A "SHALL" VS. "SHOULD" CHALLENGE?
Should you take this quiz on “shall” versus “should”? It should prove to be a quick challenge!
Question 1 of 6
Which form is commonly used with other verbs to express intention?
Origin of cardinal number
First recorded in 1585–95
Words nearby cardinal number
cardinalate, cardinal beetle, cardinalfish, cardinal flower, cardinality, cardinal number, cardinal numbers, cardinal point, cardinal points, cardinals, cardinal sign
Dictionary.com Unabridged Based on the Random House Unabridged Dictionary, © Random House, Inc.
2022
How to use cardinal number in a sentence
“Our members continue to face a number of challenges,” she said.
The Republican War on Kale|Patricia Murphy|January 7, 2015|DAILY BEAST
The number of dissenters though is unprecedented in the modern era.
Democrats Accidentally Save Boehner From Republican Coup|Ben Jacobs, Jackie Kucinich|January 6, 2015|DAILY BEAST
Starting under Theodore Roosevelt and Howard Taft, embassies headed by career diplomats increased in number.
U.S. Embassies Have Always Been for Sale|William O’Connor|January 2, 2015|DAILY BEAST
The number of diplomats was pitiful (45 appointees in 1860), as was the amount of money allocated to them.
U.S. Embassies Have Always Been for Sale|William O’Connor|January 2, 2015|DAILY BEAST
Jett sees this number as a marker of how much the president allows professionals to do the job.
U.S. Embassies Have Always Been for Sale|William O’Connor|January 2, 2015|DAILY BEAST
The country is well inhabited, for it contains fifty-one cities, near a hundred walled towns, and a great number of villages.
Gulliver's Travels|Jonathan Swift
We had six field-pieces, but we only took four, harnessed wit twice the usual number of horses.
Blackwood's Edinburgh Magazine, No. CCCXXXIX. January, 1844. Vol. LV.|Various
There are a number of bacilli, called acid-fast bacilli, which stain in the same way as the tubercle bacillus.
A Manual of Clinical Diagnosis|James Campbell Todd
Five of the number had studied with Liszt before, and the young men are artists already before the public.
Music-Study in Germany|Amy Fay
I do not think the average number of passengers on a corresponding route in our country could be so few as twenty.
Glances at Europe|Horace Greeley
British Dictionary definitions for cardinal number
cardinal number
cardinal numeral
noun
a number denoting quantity but not order in a setSometimes shortened to: cardinal
maths logic
- a measure of the size of a set that does not take account of the order of its membersCompare natural number
- a particular number having this function
Compare ordinal number
Collins English Dictionary - Complete & Unabridged 2012 Digital Edition © William Collins Sons & Co.
Ltd. 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Scientific definitions for cardinal number
cardinal number
[ kär′dn-əl ]
A number, such as 3, 11, or 412, used in counting to indicate quantity but not order. Compare ordinal number.
The American Heritage® Science Dictionary Copyright © 2011. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
cardinal number | it's... What is a cardinal number?
Aleph-zero, the smallest infinite cardinal.
Cardinal number or shortly cardinal in set theory is an object that characterizes the cardinality of a set. The cardinal number of any set A is denoted as | A | or Card A .
For a finite set A, the cardinal number |A| is a natural number, which means the number of elements of this set. For infinite sets, the cardinal number is a generalization of the concept of the number of elements.
Although the cardinal numbers of infinite sets are not reflected in natural numbers, they can be compared. Let A and B be infinite sets, then the following four cases are logically possible:
- A ~ B and | A |=| B |.
- There is a one-to-one correspondence between the set A and some own subset B' of set B . Then we say that the cardinality of the set A is not greater than the cardinality of the set B and write | A |≤| B |.
- The set A is equivalent to some subset of the set B , and vice versa, the set B is equivalent to some subset of the set A , that is, A ~ B' ⊆ B0009 B ~ A' ⊆ A . According to the Cantor-Bernstein theorem, in this case, A ~ B is fulfilled, i.e. | A |=| B |.
- There is no one-to-one correspondence between set A and any subset of set B and there is also no one-to-one correspondence between set B and any subset of set A .
It follows from this that the cardinalities of the sets A and B are not comparable.
However, deeper research in set theory has shown that, relying on the axiom of choice, it is possible to prove the impossibility of the existence of the fourth case.
Thus, the cardinalities of any two sets A and B are always comparable. That is, for cardinal numbers | A | and | B | arbitrary sets A and B , one of the three relations holds: | A |=|B|, | A |≤| B | or | B |≤| A |. If | A |≤| B |, but the set A is not equivalent to the set B , then | A |<| B |.
|
Contents
|
Aleph numbers
Cardinal number of set N all natural numbers (and hence any countable set) are denoted by (read "aleph-zero").
The cardinal number of continuum sets is denoted c or ("aleph-one"). The following cardinal numbers in ascending order denote Cantor proved that there is no set of the greatest cardinality, that is, there is no greatest cardinal number.
The Continuum Hypothesis
The Continuum Hypothesis states that there is no set whose cardinal number lies between the cardinal number of the set of natural numbers and the cardinal number of the set of real numbers , that is, < < .
See also
- Power of set
- Ordinal number
- Cantor-Bernstein theorem
- Continuum hypothesis
References
- Hans Hahn, Infinity , Part IX, Chapter 2, Volume 3 of The World of Mathematics . New York: Simon and Schuster, 1956.
- Paul Halmos, Naive set theory . Princeton, NJ: D. Van Nostrand Company, 1960. Reprinted by Springer-Verlag, New York, 1974. ISBN 0-387--6 (Springer-Verlag edition).
- Weisstein, Eric W. Cardinal Number at Wolfram MathWorld .
- Cardinality at ProvenMath formal proofs of the basic theorems on cardinality.
- Undergraduate Set Theory more proofs about cardinality - includes proof of infinite cardinal addition in Section 4.2.
Mat. logic, foundations of mathematics, theory of algorithms
Messages without replies | Active Topics | Favorites
Forum Rules
You cannot create new topics in this section.
If you want to ask a new question, then do not add it to an existing topic, but create a new one in the root section "Help me solve / figure it out (M)".
If you post a new question in an existing thread, your post and all replies to it may be deleted without warning if format or other forum rules are violated.
Do not look for freebies on this forum, the rules prohibit participants from posting ready-made solutions to standard learning problems.
The author of the question is obliged to give his attempts to solve and indicate specific difficulties.
Be sure to review the Rules topic in this section, otherwise your topic may be deleted or moved to Quarantine and you will never know why.
| xmaster |
| |||
|
| |||
|
| ||||
Actually, the question is: How to define this economy formally? | angor6 |
| ||
|
| ||
|
| |||
ru/718-kardinalnoe-chislo.html
| ||||
04/27/09 |
| |||
|
| ||||
Actually, the question is: How to define this economy formally? | Someone |
| |||
|
| |||
|
| ||||
| ||||
04/27/09 |
| |||
|
| ||||
| Someone |
| |||
|
|
