Limit math is fun
Limits - Evaluating
You should read Limits (An Introduction) first
Quick Summary of Limits
Sometimes we can't work something out directly ... but we can see what it should be as we get closer and closer!
Example:
(x2 − 1) (x − 1)
Let's work it out for x=1:
(12 − 1) (1 − 1) = (1 − 1) (1 − 1) = 0 0
Now 0/0 is a difficulty! We don't really know the value of 0/0 (it is "indeterminate"), so we need another way of answering this.
So instead of trying to work it out for x=1 let's try approaching it closer and closer:
Example Continued:
| x | (x2 − 1) (x − 1) | |
| 0.5 | 1. | |
| 0.9 | 1.90000 | |
| 0.99 | 1.99000 | |
| 0.999 | 1.99900 | |
| 0.9999 | 1.99990 | |
| 0.99999 | 1.99999 | |
| ... | ... |
Now we see that as x gets close to 1, then (x2−1) (x−1) gets close to 2
We are now faced with an interesting situation:
- When x=1 we don't know the answer (it is indeterminate)
- But we can see that it is going to be 2
We want to give the answer "2" but can't, so instead mathematicians say exactly what is going on by using the special word "limit"
The limit of (x2−1) (x−1) as x approaches 1 is 2
And it is written in symbols as:
limx→1x2−1x−1 = 2
So it is a special way of saying, "ignoring what happens when we get there, but as we get closer and closer the answer gets closer and closer to 2"
| As a graph it looks like this: So, in truth, we cannot say what the value at x=1 is. But we can say that as we approach 1, the limit is 2. |
Evaluating Limits
"Evaluating" means to find the value of (think e-"value"-ating)
In the example above we said the limit was 2 because it looked like it was going to be. But that is not really good enough!
In fact there are many ways to get an accurate answer. Let's look at some:
1. Just Put The Value In
The first thing to try is just putting the value of the limit in, and see if it works (in other words substitution).
Example:
| limx→10x2 | 102 = 5 |
Easy!
Example:
| limx→1x2−1x−1 | (1−1)(1−1) = 00 |
No luck.
Need to try something else.
2. Factors
We can try factoring.
Example:
limx→1x2−1x−1
By factoring (x2−1) into (x−1)(x+1) we get:
limx→1 x2−1x−1 = limx→1 (x−1)(x+1)(x−1)
= limx→1 (x+1)
Now we can just substitiute x=1 to get the limit:
limx→1 (x+1) = 1+1 = 2
3. Conjugate
For some fractions multiplying top and bottom by a conjugate can help.
| The conjugate is where we change the sign in the middle of 2 terms like this: |
Here is an example where it will help us find a limit:
| limx→4 2−√x4−x | Evaluating this at x=4 gives 0/0, which is not a good answer! |
So, let's try some rearranging:
| Multiply top and bottom by the conjugate of the top: | 2−√x4−x × 2+√x2+√x | |
| Simplify top using (a+b)(a−b) = a2 − b2: | 22 − (√x)2(4−x)(2+√x) | |
| Simplify top further: | 4−x(4−x)(2+√x) | |
| Cancel (4−x) from top and bottom: | 12+√x |
So, now we have:
limx→4 2−√x4−x = limx→4 12+√x = 12+√4 = 14
Done!
4.
Infinite Limits and Rational Functions | A Rational Function is one that is the ratio of two polynomials: | f(x) = P(x)Q(x) | |
| For example, here P(x) = x3 + 2x − 1, and Q(x) = 6x2: | x3 + 2x − 16x2 |
By finding the overall Degree of the Function we can find out whether the function's limit is 0, Infinity, -Infinity, or easily calculated from the coefficients.
Read more at Limits To Infinity.
5. L'Hôpital's Rule
L'Hôpital's Rule can help us evaluate limits that at first seem to be "indeterminate", such as 00 and ∞∞.
Read more at L'Hôpital's Rule.
6. Formal Method
The formal method sets about proving that we can get as close as we want to the answer by making "x" close to "a".
Read more at Limits (Formal Definition)
L'Hopital's Rule
L'Hôpital's Rule can help us calculate a limit that may otherwise be hard or impossible.
L'Hôpital is pronounced "lopital". He was a French mathematician from the 1600s.
It says that the limit when we divide one function by another is the same after we take the derivative of each function (with some special conditions shown later).
In symbols we can write:
limx→cf(x)g(x) = limx→cf’(x)g’(x)
The limit as x approaches c of "f-of−x over g-of−x" equals the
the limit as x approaches c of "f-dash-of−x over g-dash-of−x"
All we did is add that little dash mark ’ on each function, which means to take the derivative.
Example:
limx→2x2+x−6x2−4
At x=2 we would normally get:
22+2−622−4 = 00
Which is indeterminate, so we are stuck. Or are we?
Let's try L'Hôpital!
Differentiate both top and bottom (see Derivative Rules):
limx→2x2+x−6x2−4 = limx→22x+1−02x−0
Now we just substitute x=2 to get our answer:
limx→22x+1−02x−0 = 54
Here is the graph, notice the "hole" at x=2:
Note: we can also get this answer by factoring, see Evaluating Limits.
Example:
limx→∞exx2
Normally this is the result:
limx→∞exx2 = ∞∞
Both head to infinity.
Which is indeterminate.
But let's differentiate both top and bottom (note that the derivative of ex is ex):
limx→∞exx2 = limx→∞ex2x
Hmmm, still not solved, both tending towards infinity. But we can use it again:
limx→∞exx2 = limx→∞ex2x = limx→∞ex2
Now we have:
limx→∞ex2 = ∞
It has shown us that ex grows much faster than x2.
Cases
We have already seen a 00 and ∞∞ example. Here are all the indeterminate forms that L'Hopital's Rule may be able to help with:
00 ∞∞ 0×∞ 1∞ 00 ∞0 ∞−∞
Conditions
Differentiable
For a limit approaching c, the original functions must be differentiable either side of c, but not necessarily at c.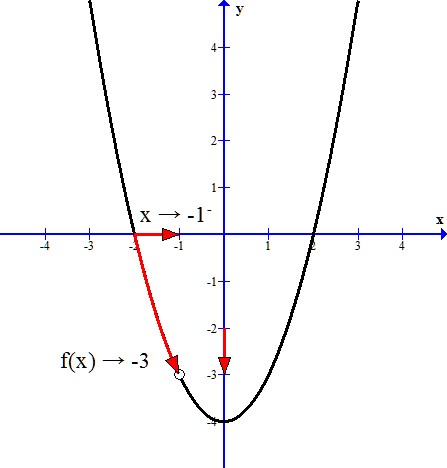
Likewise g’(x) is not equal to zero either side of c.
The Limit Must Exist
This limit must exist:limx→cf’(x)g’(x)
Why? Well a good example is functions that never settle to a value.
Example:
limx→∞x+cos(x)x
Which is a ∞∞ case. Let's differentiate top and bottom:
limx→∞1−sin(x)1
And because it just wiggles up and down it never approaches any value.
So that new limit does not exist!
And so L'Hôpital's Rule is not usable in this case.
BUT we can do this:
limx→∞x+cos(x)x = limx→∞(1 + cos(x)x)
As x goes to infinity then cos(x)x tends to between −1∞ and +1∞, and both tend to zero.
And we are left with just the "1", so:
limx→∞x+cos(x)x = limx→∞(1 + cos(x)x) = 1
90,000 mathematics is fun - regional newspaper Ogirk.ru
Simon Singh
Simpsons and their mathematical secrets
Publisher: “Mann, Ivanov and Ferber”, 2016
Although Simpsons for a quarter of a century already tired of the order, but this show must be given its due, without its fantastic success there would be neither South Park, nor Futurama, nor American Dad, nor Griffins, nor many other equally popular animated series.
Naturally, Time magazine's "best television series of the century" could not attract serious researchers. Dissertations have been defended on The Simpsons, dozens of books have been written. For example, the authors of the book The Simpsons and Philosophy (“The Simpsons as Philosophy”) note the connection between various episodes of the series and issues that worried Aristotle, Sartre and Kant in their time.
The book contains the chapters "The Moral Motivation of Marge", "The Moral World of the Simpson Family in the Light of Kant's Teachings", and "Thus Says Bart: Nietzsche and the Virtues of Vice". And the collection of essays, The Psychology of The Simpsons, says that Springfield's most famous family helps us gain a deeper understanding of the human mind. Mark Pinsky, in The Gospel According to The Simpsons, sanctifies the religious issues that are addressed in The Simpsons.
Simon Singh approaches The Simpsons from a completely unexpected angle, from the side of mathematics. And this is not the fruit of the author's sick imagination. “The fact is that many writers of The Simpsons are addicted to numbers, and their innermost desire is to introduce mathematics into the subconscious of viewers drop by drop. In other words, for more than two decades, we have been tricked into watching an animated introduction to completely different areas of mathematics, from calculus to geometry, from pi to game theory, from infinitesimal to infinitely large,” Sing writes.
And he backs up his statement with facts. The team of screenwriters that launched the project, almost half consisted of mathematicians. David Cohen - BS in Physics, Harvard University, J. Stuart Burns - BS in Mathematics, Harvard University, Al Jean - BS in Mathematics, Harvard University, Ken Keeler - BS in Applied Mathematics, Harvard University, Jeff Westbrook - BS in Physics, Harvard University. Of course, people who traded a scientific career for a career as a screenwriter did not forget about their first passion and brought a lot of mathematical humor and jokes for nerds to the series.
The author analyzes this humor and jokes episode by episode in his book, proving that although mathematics is a serious science, mathematicians are cheerful people, and when they break through to power in the series, it only benefits him. And, perhaps, the fact that comedy writers with serious mathematical training worked on the series was one of the components of its success.
Simon Singh's book is not just a guide to the math humor in The Simpsons, but it's also a great story about the mathematical concepts themselves and the theorems that underlie this or that joke.
Undoubtedly, after reading The Simpsons and Their Math Secrets, your level of mathematical knowledge, as well as knowledge of the series, will increase significantly. Well, knowledge, as you know, is not superfluous, information is superfluous, but this is not the case.
What influences the interest of schoolgirls in the exact sciences. "Paper"
August 30, 2018
Research Department "Paper" , together with JetBrains, conducted a study to find out why girls study less than boys in physics and mathematics schools, and what can change the situation. We talked to teachers, students and their parents. The study lasted 7 months, covered 6 of the strongest physics and mathematics schools in St. Petersburg and 113 people.
In order to talk about the main conclusions of this work, the editorial staff of Paper made a special project - with stories of graduates and parents who sent their daughters to physics and mathematics, interviews with a psychologist and the authors of the study themselves.
Why do girls lose interest in math in high school, in which schools are they considered less capable in the exact sciences, and how does competition hinder academic success?
JetBrains Social Projects Specialist Daria Kholodova and Head of Research Papers Anastasia Kudryavtseva talks about the origin of stereotypes about girls in mathematics and what parents and teachers think about gender imbalance.
Performance by Anastasia Kudryavtseva and Daria Kholodova at the Campus festival.Photo: Alexander Palaev
Anastasia Kudryavtseva: The original purpose of the study was applied: we wanted to understand why there are fewer girls [in physics and mathematics schools] and what needs to be done to increase their number.
We had several blocks: interviews with teachers, parents and focus groups with children. At the first stage, we talked with high school students.
We had two focus groups, which included girls from grades 10–11 of the best mathematical schools in the city. We realized that the formation of interest in the subject and the rejection of it occurs much earlier than in high school. That is, it is necessary to look not at the junction of school and university, but at the junction of middle and high schools. At the second stage, we decided to go down a few steps and conducted a study in grades 5-7 - with both boys and girls.
We talked to the parents of the girls, but we didn’t have time to talk to the parents of the boys, we want to talk with them and the parents of the older group students in order to look at the formation of the image of the future. For children in high school, it is already more conscious. That is, we want to create a more complete picture and look at the differences in the life strategies and scenarios of boys and girls.
Daria Kholodova: Basic stereotypes: women cannot think analytically; they have some kind of special “female logic”, so none of them are mathematicians; women are not up to difficult tasks, and in principle they do not need them, because their main task in life is to get married and give birth.
You don’t need any high professional goals and you shouldn’t overwork in general. Math is hard, physics is hard too. Girls don't go there - and that's good.
There is also a stereotype that girls have something wrong with hormones. It's a lot of fun, because hormones explain everything. We noticed that in more prestigious lyceums, if the teacher thinks that girls are doing something worse, he says: girls [come] puberty, hormones, they think about boys all the time. In less prestigious lyceums, teachers said that boys had hormones, a transitional period, they only think about girls.
It is often said that at some point in girls, some “masculine” instincts turn on, and for some reason this also interferes with them in mathematics. Nothing interferes with literature and languages, but there is some hormonal trouble with mathematics.
They also say that girls are simply not interested: leave them alone, it just happened that way.
Look at small children: a boy is taking apart a car, and a girl is nursing a doll. And the fact that you yourself gave the girl a doll, and the boy a car, for some reason is hushed up.
There was one informant who said about women mathematicians: “Well, there are, of course, some out there, but are they really feminine? These are not real women." And she said to herself: yes, I am a mathematician, but a teacher.
In more prestigious lyceums, they say: “Girls don’t think in an original way, they are assiduous and can work well, but you won’t achieve any success like that.” And in less prestigious lyceums they say: “Maybe girls cannot come up with something original, but they can work very well, and this is the most important thing in mathematics, so they succeed there. Boys, perhaps, can come up with something original, but they are too lazy. That is, the same alignment, but in one case it is described as conducive to success, and in the other as not conducive.
Anastasia: But we know all this from the words of teachers, we did not check who is more successful there and who really goes into IT.
Anastasia: Parents have stereotypes about girls in mathematics, but they are less rationalized. For example, in mixed families, where there is a daughter and a son who graduated from Mathematics or studies there, the parents said that for a boy a mathematical education is logical. I asked: “And for your daughter, why does this seem strange to you?” And they said something like: “Well, we somehow felt that this was not for a girl. So we gave her to the theater, to music and art schools. Stereotypes come from what parents usually do with their daughters: they usually give them to dances - well, I will give them to dances.
But we need to make allowances for the fact that parents listen to their children. And if they see that their daughter wins mathematics olympiads, solves problems in her free time and goes to mathematical circles, then, as a rule, they do not ignore it.
They consult with someone who is more competent in this area, ask teachers at school or someone they know who works in the technical field of mathematical directions. They are confirmed that the child has abilities, and the parents still send their daughter to a mathematical lyceum.
If parents do not have a specific mathematical background, then they have a long way to go to accept that the child is interested in what they do not understand. But more everyday things are also important. The parent thinks: “I don’t understand mathematics, which means that if my child has problems, then I will have to hire a tutor, this is an additional burden on both the child and the budget.”
Another factor is the location of the school. If we are talking about elite establishments, they are not tied to the area. It may happen that the school is located in the center, and you live on Zvezdnaya. And you need to come to terms with the fact that every day the child will have to be transported for two hours.
You need to be sure that there will be some kind of output, that education at this school will pay off the time, costs and fatigue of a child who spends four hours on the road. It would seem that small things, but together they lead to a very long decision-making process.
Daria: I read a study by the Higher School of Economics, which said that people with mathematical education have their own system of values. Such a cult of mathematical rationalism. They are very fond of saying that mathematics organizes consciousness. If you can decompose something into formulas, then you can solve it. And it seems to me that there is a cultural confrontation between mathematicians and the humanities. Mathematicians like to say that in principle they think better than the humanities. If parents are humanitarians, they will simply feel like strangers in a culture that is presented as elitist, so they do not seek to associate their child with it.
Daria: I have a theory that girls are simply not oriented towards professional development.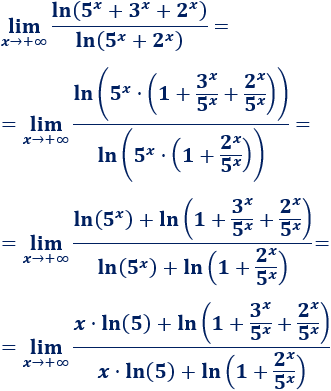
The girl is brought up so that she is not bored with life. As parents sometimes think, in principle, she does not need a highly paid job, because she needs to get married and stay at home with children. Therefore, you can do things that are potentially cool: dancing, drawing. No one cares whether she will earn money on this or not.
Anastasia: I have a hypothesis that parents want to give girls more choices. It is important for them that their daughter enjoys the profession. They all stand out: “I want my daughter to love her profession. If this is programming and she enjoys it, then please. But the main thing is that she does not earn a lot of money, but that she likes it. And for this they give a wider range of choices: you can dance, you can write poems, draw, study languages, neuroscience. Perhaps that is why it is not always the one that is harder to win.
Daria: And it also seems to me that they are not oriented towards competition.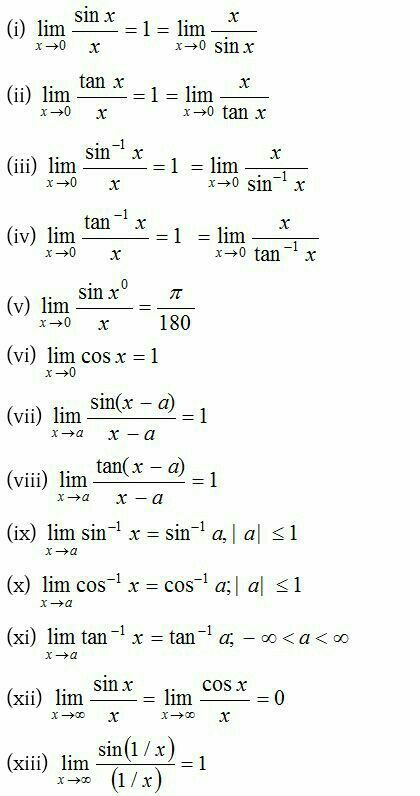
You are often told: “You are a girl, you need to be guarded all the time, take care of yourself, it’s better not to go there, it’s too hard there.” From the very beginning, they say that you are fragile and will fall apart if there is any difficulty. Then it is more difficult to make a choice in favor of something that is very competitive and where you need to invest more effort: it already seems to yourself that it is better to save yourself.
Anastasia: I read another HSE study, which talks about the impact of a competitive atmosphere and requirements at school on a graduate's future paths. The authors wrote that from weaker schools, where the atmosphere is friendlier, children were more likely to get into some cool universities than children from supercompetitive schools. When you have an oppressive atmosphere in the classroom (despite the fact that you are higher in level than children from ordinary schools), you understand that here you are an average student.
And as a result, such children do not even apply to strong universities, and those who succeed in a secondary school do: they think they are successful.
I am not going to say a sociological thing now, but it is the less competitive environment at school that will help girls become more confident when teaching mathematics. Internal anxiety is formed due to the fact that open ratings for students hang: who is the most successful and unsuccessful. The atmosphere in which you constantly have to compete hinders everyone who does not feel confident enough in this area; who is more receptive emotionally; who need a little more time to understand the material.
Daria: I think girls feel much more comfortable when working in a group. Therefore, if there is some kind of group competition where you need to win, then they assemble a team of girls: they cooperate very well and will tear everyone apart. I like the stereotype that girls are less competitive.
And it seems like everyone should be doing this. Less competition and more cooperation.
Anastasia: When we interviewed teachers, they said that, according to their observations, the decline in interest in mathematics occurs at 8–9class. Before that, everyone is doing the same thing, everyone seems to be interested. And then something happens, and in the 10th or 11th grade, the girls abruptly change direction.
After the focus groups, I was a little upset: the girls are thinking about the future and about education, based on the fact that marriage, and necessarily financially successful, will stand in their way as an insurmountable iceberg. In grades 10-11, not everyone, but some expressed the idea that a woman does not have to earn a lot, she does not have to support her family. Suppose, of course, I am interested in doing oncological research, but I study there for seven years, and I need to start a family.
This is not a quote, but a formulated thought.
There is a compromise, but it is, as a rule, at the intersection of regions. Smart, erudite children study in lyceums, who understand that they have a lot of ways for realization. They don't want their math background to disappear, but they also don't want to do just math and just programming. They are looking for something in between. For example, if I go to work in IT, I want to become a manager, not a coder. Then you don't need to know serious programming, it's less competitive, it's working with people, it seems more interesting and less rigid. It seems like you can find time for something other than work.
As for the interest in the subject, there were girls who understood that the winners of the Olympiads are usually boys: why go to this Olympiad if I do not win? I will go to the Olympiad, which will give me admission to the university. It is simpler, there are fewer people, the applied goal is fulfilled.
They are very rational approach to solving this problem.
In the middle link (grades 5-6) everything is different. Everyone wants to be programmers and engineers. When we asked what professions they are interested in, what they want to become, girls in different schools most often named professions that are directly related to technology and mathematics. None of them said anything along the lines of “I don't think I can succeed,” as girls in grades 10 and 11 used to say.
5th-7th grades are the period when girls, most likely, just came to math school. They have recently started participating in olympiads and competitions, they are interested in everything. Everything works out for them and so far there is no this realization that they are losing or that for some reason they are worse than others. We cannot yet say what things affect this gap (gap - approx. "Papers" ) - this is something we will check in the future.
Now we have hypotheses from which we can start, but we will not dare to say that any of them has been confirmed.
Daria: There are various theories and studies, for example, the theory of gender actualization, according to which the older a girl gets, the more she associates herself with her own gender. But this theory has been debunked by many. Maybe the idea is being updated that we should already think about the profession. The idea is not just that “I will probably be a programmer someday”, but that now it is already necessary to choose a university.
Anastasia: Before every interview, I spent 10–15 minutes explaining why we were doing the research. That is, the person seemed to have agreed to meet, but like this: “What are you doing in general? Everything is fine with us, there is no imbalance.” As a rule, this problem did not matter in the eyes of the informants. This happened in prestigious lyceums, but we remember what stereotypes there are.
Daria: In the non-prestigious, just the opposite. In an interview, the informants said: yes, parents have convictions (and they generally have them) that mathematics and physics are not women's spheres. Parents often orient girls to other subjects, and therefore they simply do not come to specialized schools. And if they do, then less effort is invested in the study of mathematical subjects. This is what a sociologist might say.
We discussed with the teachers of the courses that train Olympiads how to show parents that mathematics is easier than it seems. Teachers basically say that the main thing is to tell that there are girls who become winners of the Olympiads and at the same time they have everything in order in life, they look good and are generally normal, they just worked hard. In general, we agreed that we should tell everyone about such positive examples and make them visible.
Anastasia: The focus groups were not high school boys, but 5th-7th grades.
At this age, children are not very reflective about this. We had questions like, "Describe a student who has trouble with math in class." We have not hinted that gender should be the criterion. But in more prestigious lyceums they said: "Well, some kind of girl." And when I asked why, they did not answer that girls are stupid or that they are dumber, they said that girls are more interested in something else - literature, languages.
When we listen to this, we think: well, there is probably no problem, since they are less interested. And then we listen to the stories of girls who say: “I felt weak for so long that I wanted to go into a sphere where I could succeed.” And this is an important argument for me in a situation where someone tells me that this is my own choice.
Sometimes the boys said: “Look, all kinds of engineers and mathematicians are men. They're doing better." I asked why men are better at it. "Because there are more of them in those directions.
" That is, it is a vicious circle, and the students do not really understand this.
Daria: It's interesting that the teachers have the same thing. When you ask them why there are more boys in math, they say: “Statistically, there are more boys. What's incomprehensible?"
There is the concept of “gender order”, which says that status and resources are always distributed towards male gender, because we live in a patriarchal gender order. There is an article by Nathan Ensminger who wrote about how programming has gradually become masculine. At first, programming was considered a female profession, but then, as soon as it became prestigious, it began to be considered a male occupation. And, as a result, people began to say that he needed skills. This became a kind of explanation of why women cannot do programming.
The same thing happened with the teaching profession: it was considered cool, and the teachers were men.
