Math help for kindergarteners
Kindergarten Math Tips: Curriculum for homeschool
Hoping to help your kindergartner with math skills? These basic tips from our kindergarten curriculum guide are what experts suggest.
Incorporate basic math concepts
Try to incorporate basic math concepts into everyday activities. Have your child count objects regularly and pose easy counting challenges, such as counting the number of steps on a flight of stairs or the number of red cars you see while driving. Take opportunities to count by twos or fives or tens, for example, if you've bought many of the same item at the grocery store or need to count a pile of coins.
Practice shape recognition
Practice recognition of different shapes. Have your child spot things that are triangular, like pieces of pizza or the roof of a house, or rectangular, like paper money. As you talk about different shapes, have her describe why a shape she spots is a triangle (three sides) or a square (four equal sides) or a rectangle (two opposite equal sides and two other opposite equal sides of longer length).
Solve jigsaw puzzles
Doing puzzles is a great way to develop important visual discrimination skills, or the ability to recognize differences and similarities in shape, form, pattern, size, position, and color.
Apply math in everyday life
It's especially memorable to children when they can use their new math concepts in their everyday life. Have your child arrange their favorite stuffed animals in a circle for a party and give two or three crackers to each toy. Have them add up the total number of crackers distributed. Ask them to predict how many more crackers they would need if one of their toy action figures joined the party. Then ask them to predict the total number of crackers needed with yet another guest. This gives them an opportunity to "add up" in their heads and then see if they are correct when they actually add the next figure and count up the new total. The game can be played in reverse when one of the figures leaves the party, taking their crackers with them.
Play more or less
Think of a number for your child to guess. After each guess, respond with the words "higher" or "lower." At different times use the words "more" or "less," so your child learns different arithmetic vocabulary. This game helps correlate number words and counting sequence with actual amounts or sizes.
Practice sequencing
Practice sequencing with your child to develop their ability to recognize and store math procedures and number sequences. Make a peanut butter and jelly sandwich or build a snowman together, then ask them to describe in order the actions that took place. Your child can also describe the sequence of events that took place in the day, in a movie they saw, or in a story they read.
Develop an understanding of units of time
Use a timer for activities like watching TV or using the computer, so that your child becomes familiar with the concept of time and how long different units of time last. If your child doesn't want to leave the playground, say they can stay for five more minutes.
They will start to develop an understanding of time and how long different units of time last if you do this regularly.
Learn to count money
Give your child a piggy bank and help fill it with spare change. Every month, empty it together and have your child sort the coins by denomination. Have him match the coins to the denominations indicated on coin wrappers, which can be obtained from some banks or purchased inexpensively. This will help your kindergartner with counting, value recognition, and sorting, as well as hand-eye coordination.
Play music
Music is a great way for your child to engage with concepts related to math. Practicing an instrument means learning about tempo, measure, and meter - all of which involve math.
Play family games with math
Plenty of family games incorporate math. Tic-tac-toe, Connect Four, and dominoes are just some of the many games that help build math skills.
To find out what your kindergartner will be learning in math class, check out our kindergarten math skills page.
TODAY's Parenting Guide resources were developed by NBC News Learn with the help of subject-matter experts, including Joyce Epstein, Director, Center on School, Family and Community Partnerships, Johns Hopkins University; Pamela Mason, Program Director/Lecturer on Education, Harvard Graduate School of Education; Denise Walston, Director of Mathematics, Council of the Great City Schools; Nell Duke, Professor, University of Michigan; Leanna Baker, Retired Math Teacher; Bon Crowder, Math Teacher and Blogger, MathFour.com; and Robin Schwartz, VP, Association of Teachers of Math of NYC, and align with the Common Core State Standards.
7 Tips for Helping Your Child with Math at Home
If you feel lost when your child asks for help learning mathematics, you can take comfort in knowing you’re not alone. Teachers, parents, and PhD students—even biologists, chemists, and physicists—sometimes feel daunted by math. Add to that the fact that math education isn’t as static as we might like it to be.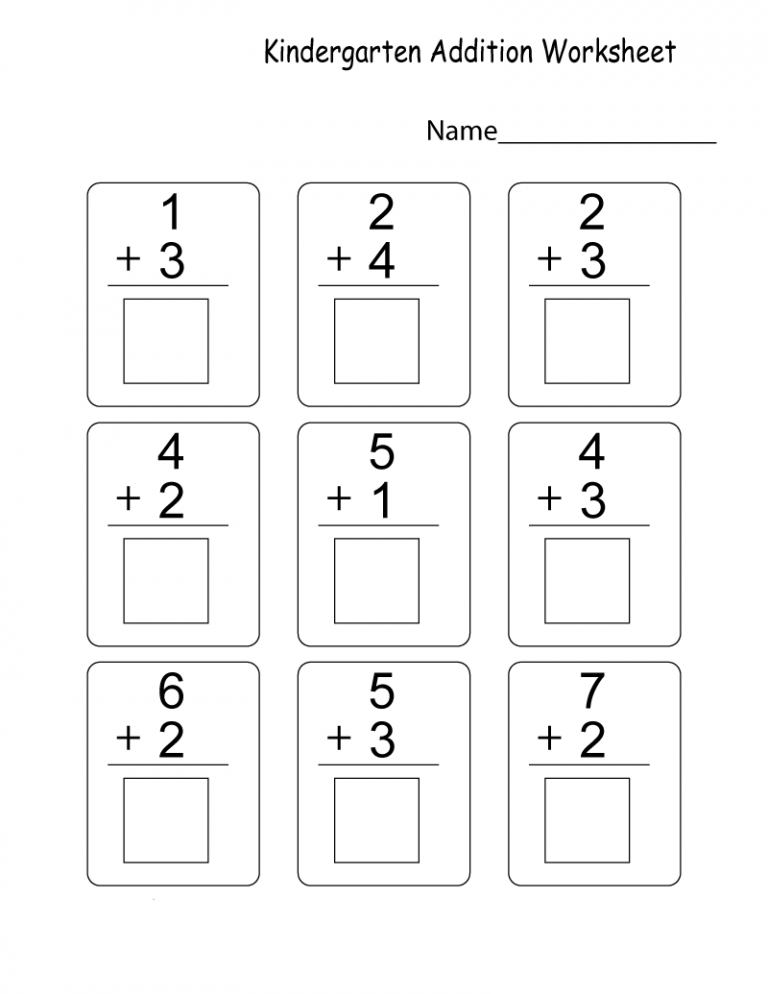
As we better understand learning and the human brain, the ways in which we teach math inevitably evolve. For many, the sorts of problems and strategies that comprise the “new math” can seem impenetrable.
But fear not! There is hope with growing evidence that your reaction to math, while completely understandable, is more related to how your parents, teachers, and peers talked about it than anything related to your brain.
You don't have to go from math phobic to mathematician overnight, but here are some tips to help foster the math whiz in your child.
1. Avoid saying you’re bad at math. Stay positive!
This is probably the most far-reaching tip in terms of how much it will benefit your child. If you feel inclined to say something like “It’s fine that you’re bad at math, so was I,” bite your tongue! Counterintuitive to many, research suggests that the concept of being a “math person”—or not—is a myth. Even if that’s firmly how you feel right now, one of the best ways to avoid passing math anxiety on to your children is by steering clear of negative messages about math.
Instead, try focusing on difficulty and effort by saying things like, “I understand how difficult this is for you. It was difficult for me too,” or “Don’t worry if it feels like math problems take more effort than some of your other assignments. You may not understand it yet, but I am confident we can work it out together.”
Additional Resources
- “What Does It Mean to Have a Limitless Mind” blog post (includes book excerpt)
- “Healthy Habits for a Growth Mindset in Math” blog post (includes free poster)
- Method to the Mathness podcast, Season 2, Episode 3 (“Math Positive Mindsets” featuring Dr. Carrie Cutler; also see her book Math-Positive Mindsets: Growing A Child's Mind Without Losing Yours)
2. Talk about math.
Talking about math doesn’t have to mean making a nuanced statistical analysis or debating what equation best models a phenomenon. Talking about math can be as simple as counting clouds or guessing heights.
This is especially crucial for young children who need to feel comfortable just thinking about math and seeing that it is a part of the world. Depending on the age of your child, find ways to incorporate math into any topic you’re talking about as the opportunity arises:
- How many is that? How many would I have if I had another one?
- What would half of that look like?
- How could I split this equally?
- How do you predict this trend will change over time?
- What’s the chance of that happening?
- How can you make that more abstract? (The whole purpose of mathematics is to take ideas and make them abstract!)
- How many cards will you draw?
If you don’t feel comfortable talking about math, look for other ways for math to be a part of your child's discourse and experiences. Consider watching movies and television together that feature math (for example, CBS’s former TV show Numb3rs for older students) or even simply hanging math-related posters near where your child typically studies.
Additional Resources
- HMH Into Math Anchor Chart Posters (Grades K–8)
- Supporting the Mathematical Practices and Processes Through Questioning Poster
3. Frame this moment as a chance for kids to explore whatever math question interests them.
Most teachers must get through a particular set of standards every year. That can leave students who are curious about an unrelated part of math disappointed or frustrated because there simply isn’t enough time to explore it. Standards and assessments are important but try to free yourself from worrying about whether your kid’s question is too easy, too hard, or even part of the curriculum. Keep in mind that math can be an effective tool to approach nearly any question. If you’re tempted to answer a question with, “You should know this by now,” “That sounds way too hard,” or “That doesn’t matter,” instead direct the curious mind to the teacher or active math educators on social media.
How would they approach the question?
Moreover, connect math to what interests your child. Do they like animals? Have them explore how many animals are in a zoo, how much space they need, or how much they cost to obtain. Do they like fire trucks? Find out how heavy they are or how much water they can pump out in a minute. What about video games? Challenge them to record their scores in a table or graph.
Additional Resources
- Math at Work Web Series
- Real-World Mathematics at Home: 10 Investigations for Students (Math Solutions blog post)
4. Have your child teach you math.
Here’s a great way to learn something—teach it. Ask any teacher. Most will agree that even when it’s something “simple” that they could swear they knew inside and out, once they have to explain it to someone else, they’re forced to consolidate knowledge and try new ways of explaining it. When faced with a question that you can’t answer, explain that you're stuck too, and challenge your kids to figure it out just well enough that they can try to explain it to you.
Even if they help you only a little bit, they may spark insights that allow you to finish where they left off.
5. Try the new math.
If the thought of “new math” intimidates you, it's understandable. How is it your third grader is taking home math problems that stump you?! Rest assured, the “new math” is no different from the “old math.” If you double 15, you still get 30. If you multiply 6 and 3, you still get 18. It’s not that multiplication, division, and fractions have radically changed; it’s just that we now have better tools for explaining them.
One major source of contention is how multiplication that previously took just a few lines to work through now involve seemingly endless equations and diagrams. However, it's important to note that students are learning fundamental strategies that let them conceive of 6 × 3 in a way that extends to 60 × 30, 1/6 × 1/3, and 0.6 × 3,000,000. This way, they will be able to group the concept of multiplication deeply enough to lean on whatever method helps them, even the quick algorithms you might be more used to.
Instead of saying, “This is way too hard and confusing,” show the method you use as just another strategy. For example, “I've never seen multiplication this way before. Here's the method I would use. Now let's try to learn this other method together. It's hard for both of us!”
Additional Resources
- Math in Focus Grade 4 Heuristics Poster (Guidance on strategies you can try)
6. Do away with “drill and kill.”
Those of us who remember sheets full of multiplication problems to be solved quickly might have a skewed view of what it truly means to master math. Evidence suggests this is why you’re probably wary of math in the first place!
Yes, there are standards, benchmarks, and state assessments. However, those are not what make up math. The deep, multifaceted tool that is mathematics is very different from the blunt hammer that is fast arithmetic. Look for activities and projects where math is only part of the challenge.
Or look for games and puzzles where math is a code to be cracked or a grid to be solved. Count beats in music, and look for addition and multiplication in dance steps. Math should be active and playful, not worksheets of sterile and monotonous problems.
Additional Resources
- Method to the Mathness podcast, Season 2, Episode 1 (“Cathy Seeley, Tasks, Tests, and Teamwork”)
- The Giant Sculpture Gallery: A Math Puzzle (Grades 5+)
- HMH's Pinterest Math Hub
7. Take it slow.
One final word of advice. The same tools you might use to solve any problem apply here. Take breaks. Try a different way. Ask someone else. Everyone’s pace for learning math is slightly different. Consider the story of Andrew Wiles. Fermat's Last Theorem was a math problem proposed in 1637 that anyone familiar with exponents could understand, and mathematicians at the time thought would be easy to solve. Here is one way to state the problem:
Consider the list of all numbers raised to the 2nd, 3rd, 4th, etc.
powers:
- 2nd power: 1, 4, 9, 16, 25, 36,...
- 3rd power: 1, 8, 27, 64, 125, 216,...
- 4th power: 1, 16, 81, 216, 625, 1,296,...
- And so on
It is possible to find two numbers on the “2nd power” list that add to each other, for example 9 + 16 = 25. However, is it possible to find two numbers that add to each other in any other list?
British mathematician Andrew Wiles was fascinated by the problem as a child, and as an adult, was determined to solve it. He labored over it for six years until rocking the mathematical world with a solution that was over three centuries in the making. Learning math is most definitely not a race to the finish line.
* * *
Browse our full library of free teaching and learning resources to help children learn while they’re away from school.
“How I fell in love with mathematics with all my humanitarian soul”
These thoughts have been tormenting me since I started teaching mathematics.
And at one fine moment (he was really beautiful) I realized that I fell in love with this subject with all my non-mathematical soul. It turned out that everything is determined by the environment and the correct teaching methodology.
Since childhood, I have experienced a persistent hatred for this, as it seemed to me, far-fetched and senseless discipline. No, I did not dispute the fact that mathematics is vital and that people cannot do without it. But it is available only to some certain class, or even, perhaps, to some special breed of people, whose brain probably consists of some other substance than mine.
After graduating from school and having passed the exam with grief in half, I was glad, my dear, that I would never have to suffer from this "nonsense" again. How wrong I was then. But I was even more wrong when I thought that I would hate the Queen of Sciences all my life.
Everything went according to a well-known scenario. Parents are musicians, there are no mathematicians in the family.
What's the math there? The brain is not mathematical and other nonsense common in the school environment. We choked on such prejudices in childhood, retraining left-handers, “healing” stutterers with fear, and diligently sorting children’s brains into “mathematical” and “humanitarian”.
Observational tendencies with subsequent deductions made me deeply doubt my genetic genius. Yes, it is true that in a family of musicians, most likely, a successor to a musical dynasty will grow up, in a family of artists, the probability of the birth of an artist is very high, and in a family of mathematicians, it is quite possible that a child with a mathematical mindset is growing up.
And the easiest thing to do in this matter is to blame everything on genes. They are so tiny. Maybe it's true. But life has made me repeatedly convinced of something else. The decisive role in the orientation of the personality is played by the environment, the information field that surrounds the child from birth.
What will he see, what will be surrounded by a newborn baby in the artist's family? What will adults talk about when they are next to him? And in a family of musicians, where music, the voice of a mother or father sounds more often than simple speech? What will the son of a mathematician meet when he reaches the bookshelves or the desktop? Books, numbers, formulas. Silent, but exuding an extraordinary and truly magical information field. I do not deny at all that something in the genetic information is different. Let geneticists deal with this. I am talking about what I observe in life.
So, the first thought: there are no "physicists" and "lyricists". There are no "mathematical" and "humanitarian" brains, but there is an environment that determines everything. But why then is mathematics so categorically difficult, incomprehensible and inaccessible to such a large number of students in school (almost more than half)?
Second thought: mathematics is not taught in school.
Or in another way: what they pass off as mathematics is not mathematics. In the same way, in most schools, English lessons are far from the language itself, and singing lessons from music.
In all the years of schooling, I never managed to meet a mathematics teacher at school who was truly passionate about his subject and sincerely loved her. Therefore, I myself could not understand, accept, or love mathematics. There was no one at school to show me the true beauty of this science.
To serve ten years at a school desk and never see mathematics!
Instead, the teachers, conscientiously fulfilling their role, slipped me some kind of small change consisting of dry numbers, graphs and formulas, the essence of which they most likely did not understand themselves. The whole point of training was to come to the correct decision by given instructions by all means and pass the next test. I, who was born in a family of musicians, had no idea what relation to life all these graphs of functions and boats came out towards each other at the same speed.
The fact that mathematics is an art, as beautiful, diverse and multifaceted as music, sculpture or architecture, was not even known to the teachers themselves. In the school environment, mathematics is a common subject that must be passed. Passed means your brain is "mathematical", go to a technical university. Didn't pass - then you are a "humanist", and go to the musicians or study philology.
If until recently I felt it somewhere at the level of intuition, then after reading P. Lockhard's article "The Lament of a Mathematician" I just threw up my hands. Here is the explanation of the problem. Here is the answer to the question.
It's not that my brain is arranged differently, but teaching is going in the wrong way
And now, the third thought. Mathematics is best taught by ... non-professionals.
Do you remember the sayings: “If you want to know a subject perfectly, start teaching it” and “When you teach others, you learn yourself”? Consequently, only that knowledge is considered to be mastered, which was passed through itself, carefully comprehended and voiced.
In progressive educational circles today, the idea of the productivity of education is sounding more and more vividly, when the educational process is built in such a way that the student independently systematizes information in a way convenient for him and then (this is indispensable) tries to transfer this information to another. At the same time, it is quite natural that the teacher in this case is physically unable to possess the amount of knowledge of a graduate of the Faculty of Mathematics. It is enough that at the moment he is well oriented in that area of the system that he has realized. And if there is an adult in the place of the teacher: mom, dad, grandmother, who are poorly versed in mathematics?
Let's analyze how the whole learning process happens in this case. So, the story of one mother, who in childhood did not know mathematics well, but becoming a parent became so bold that, rejecting the help of the school and tutors, she took upon herself the responsibility of teaching her child mathematics on her own.
I must say right away that at the time my eldest son entered the first grade, I already felt that teaching (not only mathematics, but in general) in elementary school was turned upside down. N. Zaitsev’s methods reliably protected my motherhood and the elementary school period in my son’s education and for many years brought up a special way of pedagogical thinking in my head. In other words, in teaching mathematics “according to Zaitsev”, the main thing is to read the manuals thoughtfully and not deviate from the course. Thus, we will not only qualitatively study the material in mathematics for elementary school, but also lay a solid foundation for subsequent work in high school.
How exactly (from my own experience) does mathematics “according to Zaitsev” differ from school mathematics? More on that just a few lines later. Meanwhile, the son goes to the sixth grade. The materials developed by N. Zaitsev are running out of stock. There comes a time of confusion. Once again I face the fact that I don't know mathematics.
I don't know what to teach, nor HOW to teach. To go to school? Give up? Hire a tutor? But an inner voice convinces of the meaninglessness: “There is no mathematics there. It's useless to go there."
But where can I get it? The same article by P. Lockhart prompted the idea that mathematics should be taken from life itself. What surrounds us, how the space around us is organized, according to what laws it exists - this is mathematics, and not boring numbers on the pages of textbooks.
And now what was promised: what is the difference between mathematics "according to Zaitsev" from the corresponding discipline at school and from the mysterious "formation of mathematical representations" in kindergarten programs. In Zaitsev's methods, mathematics is a special organization of space, communication with which is built into ordinary children's life.
Mathematics for a child is life
Moreover, the meeting with mathematics begins not from a school desk or from a school preparation club and not even from a kindergarten preparatory group, but from the moment when the baby becomes able to contemplate the environment world.
Even then, while still at the level of feelings and sensations, he will know how a circle differs from a square and a triangle, long from short, wide from narrow, large from small. All concepts - angles, figures, areas, perimeters, fractions, sectors, lengths and sizes - are materialized, tangible and understandable. Zaitsev made mathematics visual and accessible to kids of a very early age, and, learning to look for and find it around him, he will continue to look for it all his life.
This is the discovery. Teaching mathematics must begin with the search for mathematics around us! It is necessary to teach the children to admire its beauty and grace. Mathematics, contrary to all established ideas, does not begin with numbers and counting.
Where does mathematics live? Just not in school textbooks. Today, with my four-year-old daughters, I began to study (no, no, to search) mathematics around us. We glue the application. House: a square and a triangle - well, what's wrong with that? How about cutting a square diagonally? You get two triangles.
This is “what is it” for you, but for a child it is a discovery. Carefully cut off the corners of the rectangle and - hocus pocus - got an oval. And how to get a circle from a square? After such "tricks" it will be easier to talk with children about inscribed and described figures.
Did it ever occur to you that the game "Battleship" is the theme "Coordinate Plane" from the textbook for the sixth grade? And chess, by the way, too. We remember the basic principle "from visual-effective to verbal-logical", and not vice versa. Let us first give the child a clear concept of where this occurs in life and how, with the help of this knowledge, he can influence the world around him.
No one here refutes the classical mathematical theory. But every great scientist first realized his discovery by experience, and then only clothed it in beautiful words. The trouble is that many of our teachers and academicians, alas, have bypassed this experimental path. They were thrown axioms and theorems like a stale crust, which they continue to chew dry, now, together with their students, not feeling either taste or aroma.
In mathematics lessons, it is necessary to resurrect and bring to the fore everything that is considered far optional in school curricula.
N. Zaitsev, in methodological accompaniments to his manuals, offers a lot of ideas for organizing such activities with children: they are simply replete with mathematical tricks, rebuses, puzzles and tasks, sometimes so original and entertaining that to deal with them without the help of an adult, a student, rather can't do everything.
The purpose of such work according to Zaitsev is to awaken thought, ingenuity, imagination, without which it is impossible to solve any vital task, educational or creative
Mastering counting skills in such an educational process is not an end in itself, but an intermediate link, a logical obstacle that is necessary overcome to solve specific problems. The child initially sees the final result of his efforts: "I want to know, decide, guess."
It turns out that the whole process of teaching mathematics should be built the other way around: first, the patterns and features of the organization of the space around us, observation of changes, movement, time.
And only after that we study how these changes and laws are reflected in mathematics. We study the numbers of the first hundred, discussing the age of parents and relatives, the multiplication table - through the area of a rectangle, the basics of geometry - through visual and effective work with the details of "Ornament".
We open a problem, we cannot solve it, we reach a dead end (oh horror) and start to analyze what laws and concepts we do not know, what relations between objects we have never paid attention to! To learn mathematics, you need to start interacting with mathematics. The same thing happens in language learning. In order to recognize the great and powerful, you need to read the great texts, quote and rewrite them, sorting out those unshakable, historically established principles on which the language rests, word by word, and not study stamped exercises from semi-literate school textbooks, which sometimes put forward very dubious versions about the true structure of the language.
When teaching children mathematics, it is necessary to monitor the quality of the material we offer them for study and observation.
And yet. How to teach a child mathematics in the conditions of family education, when the teacher himself is not too confident in his knowledge of the subject? In elementary school, the answer is clear: children learn quite successfully and easily according to the method of N. Zaitsev. So? The answer is in the word "together".
Ignorance of mathematics does not relieve me of responsibility for my child's knowledge
If you don't see, look. If you don't know - learn. And together we search, draw, subtract, peer, look for analogies. Does not work? Ask for help. But this help does not consist in ready-made solutions and answers in the style: "Here you need to do this." The concept is not realized, the solution of the problem is not given into the hands. We are not looking for a tutor who, for a certain amount, with omniscient intonations, will lay out a dry instruction or formula for us.
We try to "live" mathematics, to feel the right answer. Mathematics needs to be experienced.
Let's think: what is the point of teaching mathematics? Learn to count? This is the limit of elementary school. So? Watching the processes taking place today in secondary schools, and remembering your school childhood, you realize more and more clearly that the goal of schooling in mathematics is to prepare for the Unified State Examination. Meanwhile, every adult who takes responsibility for teaching children mathematics should understand that the essence of this process is the disclosure of the potential capabilities of children's intellect, the development of all mental processes (thinking, memory, imagination, attention), the formation of the ability to set a learning task and independently select the means to solve it.
Successfully passing the USE is very important, but this is not what makes a person happy
USE is not life, it is just a separate short-term episode.
Let's think about whether there is life after the exam? After all, our main task is to educate not a successful student who is able to score the coveted points on the Unified State Examination, but a person who creates, thinks, is enthusiastic, is able to think creatively, love and transform the world around him.
Everyone has long known that passing tests successfully is, as they say, a matter of technique, this is not a creative process. To score the required number of points, the student simply needs to be "trained" on typical tasks. For this, there are special methods and literature. But to cripple the psyche of children, starting from elementary school, distorting their understanding of mathematics, depriving them of the possibility of emotional or even sensory perception of the subject - is this the right way to understand mathematics? Hardly.
"Elephant", the results of the event among kindergarteners and graduates
winter
December 10 - 17
2015
Mathematics
Members Kindergarten, grades 1-11
Status
Results summed up
Apply Go to this year's event
Children of all ages (from kindergarteners to graduates) are invited to start the Math Marathon to test their ability to solve problems quickly, think logically, be organized and persevere.
C chalk! L wow! O organization! H stability!
Math marathon - complete the distance of 42.195 points!
The competition-game is held by age groups:
Kindergarten, Grade 1, Grade 2, Grade 3, Grade 4, Grade 5, Grade 6, Grade 7, Grade 8, Grade 9, Grade 10 and students 1 course of SPO (NPO), 11th grade and students of the 2nd year of SPO (NPO).
All participants of the Contest-game receive electronic Participant Certificates .
Coordinators who have registered 15 or more participants in the Competition-game will be sent the award material by Russian Post.
The winners and laureates of the Game Contest will receive diplomas and prizes (winners of the international level) by Russian Post.
Individual participation
Time
30-60 minutes
Results
12/29/2015
Registration of participants
until 12/17/2015
(inclusive)
Date
10.
