Home » Misc » Pre k mathematics

Pre k mathematics


The Most Important Math Concepts Kids Learn in Pre-K

Although there’s a lot of emphasis placed on emergent reading, experts show that pre-k math skills are just as important for your child’s learning development.

Understanding what skills your child will be exposed to as a math beginner will give you an idea of what concepts you can emphasize in fun, easy ways at home!

Fortunately, kids are exposed to many math concepts from a very young age — putting puzzles together, sorting objects, and even playing with building blocks. These activities all help build a good foundation for math.

In this article, we’ll take you through the most important pre-k math concepts so you can encourage and motivate your budding mathematician!

Table Of Contents

  • What Are The Components Of Pre-K Math?
  • Basic Pre-K Math Checklist
  • Pre-K Math Development
  • 9 Fun Pre-K Math Activities

What Are The Components Of Pre-K Math?

There are five basic components of pre-k math. They act like umbrella terms, each with many different elements hidden inside their broad concepts.

Your child will become acquainted with all of these essential concepts when they begin learning pre-k math.

1) Numbers And Counting

Children typically start with the bedrock of math — numbers! They’ll learn number names and how to write numbers, typically beginning with 1-10.

Counting is not easy business! While your child learns how to count — first with physical objects, then conceptually — they are bound to make mistakes here and there. This is perfectly all right. Counting will take time to master.

Most of kids’ initial exposure will be through representational counting. This could mean counting the number of strawberries in their lunch box, how many blocks are on the floor, and so on. These counting activities will set the stage for a strong foundation in counting.

By understanding that numbers represent objects, your child will begin to understand one-to-one correspondence (each object counted gets its own number and only that number) as well as the counting principle that when counting the number of objects, the last number counted equals the amount present.

Over time, a child’s reliance on physical objects for counting will decrease. They’ll depend more on conceptual counting as their skills develop.

This conceptual counting is called “number sense.” They’ll understand that quantities, whether tangible or theoretical, are countable. They’ll also learn that numbers can be compared: two or more numbers can have a more-than, less-than, or same-as number relationship.

There are many fun ways to get your child comfortable with numbers and counting at home without making it feel burdensome.

Here are a few simple yet effective strategies you can try:

  • Encourage your child to touch and count objects they see in everyday life — for example, a bunch of bananas or a stack of books.
  • After they count a set of objects, help them write down the corresponding number on a piece of paper.
  • Have your child compare different items using the appropriate language. For example, “Let’s count the number of blueberries and strawberries on the plate. Are there more strawberries than blueberries?”
  • Hang a simple number line on the wall or tape one to your refrigerator. Throughout the day, point to each number with your child and count from 1-10 together.
  • Ask your child to help set the table by counting out the right number of forks and spoons. Once they have collected them, they can count them again as they put one at each place setting.

These simple activities allow children to make sense of numbers. And the more they practice counting principles outside of the classroom, the more they’ll realize how relevant they are to everyday life.

2) Addition And Subtraction

Once your child has a firm grasp on counting and is developing number sense, they’ll explore the relationships between numbers more often. Describing how numbers are the same or different will lead into learning how to combine two numbers to make a new number!

Similar to the last concept, children will typically learn how to add and subtract by relying on counting activities with tangible objects. For example, you could set up two separate groups of apples and ask how many you will have if you join them together.

The first group may have three apples, while the second group has two apples. At first, many children will count one group and then start over to count the second group. It is a good idea to count both groups individually and then bring them together and count the total amount.

This is their first introduction to addition! The same idea works for subtracting. What happens when you begin with five apples and then take away two of them?

“Taking away” objects may be a little harder for your child to master at first. This is why many children will remove apples first and then count the remaining apples rather than counting backward.

To help, practice counting backward together. Pretend to be a rocket ship, and start counting down from five to one, gradually increasing the beginning number each time. After you get to one, shout, “Blastoff!” and jump into the air as high as you can. This fun game can help your child become more comfortable with counting down.

Pictures can also help your child master addition and subtraction concepts. For addition practice, present one sheet of paper with three apples and another with two. Then say, “Count the apples on both pieces of paper. How many apples do you have total?”

For subtraction problems, present this scenario: “On our paper, we have five apples total. How many apples will you see if I cover up two of them?” Then, count the remaining apples together.

Pictures are an effective way for your child to visualize mathematical problems. But, if you prefer not to draw, you can also use real objects instead. You could get out several apples (stuffed animals, cups, or whatever) and count them. Then, use those items for math practice.

Remember that adding and subtracting are basically making comparisons between numbers or establishing relationships between them. There are many strategies a child might use to solve a problem, which is a good thing since our main goal is to help children think mathematically.

3) Geometry And Spatial Reasoning

Shapes are everywhere in our world, which will be one of your greatest assets when it comes to teaching your child about shapes and spatial reasoning.

They’ll start out by learning about the basic 2-D shapes that are used in math: squares, triangles, circles, rectangles, rhombuses, and ovals. Learning how to draw these basic shape illustrations can be helpful for their learning process.

Some of these shapes you’ll be able to reference easily in your day-to-day life. This will help reinforce your child’s understanding of the shapes after their initial introduction.

For example, when making breakfast with your child, you could hold up a plate and ask them, “What shape is this? Do you think it’s a square or a circle?”

Other shapes, like triangles or rhombuses, may be a little harder to find hanging around. Challenge your child to find these shapes in nature. Are there any flower petals in your garden that are shaped like triangles (or an aloe vera plant hanging in their windowsill)?

Encourage your child to be creative with identifying shapes! It will help them with learning geometry in the long run.

Next, learning 3-D shapes will come after learning 2-D shapes. Like their flatter cousins, 3-D shapes are all around the world, too! Your child’s soccer ball is a sphere; the paper towel roll in the kitchen is a cylinder.

We recommend learning the basic form of these shapes and how they appear first. Then, you can use the natural 3-D shapes in your child’s environment to reinforce their learning!

Point out shapes when you see them and play a shape version of “I Spy” to practice. If your child has a set of blocks, talk about the different shapes of the blocks. Challenge them to use only one shape to build something. Then, see what they can make by using all of the shapes.

Kids also learn about spatial reasoning by discovering how to describe the shapes they see and play with. They can compare them with dimensional adjectives like “big” and “small,” or characteristics of their shape like “straight” and “curvy.”

This includes the spatial relationship between different objects, too. Look out for observations using location adverbs like “under,” “beside,” or “around.” These are all different ways for your child to “measure” or observe how shapes take up space.

4) Sorting And Patterns

We categorize things in our daily lives without even realizing it. Your child probably already does this, too — they may arrange their stuffed animals or toys in a certain way. For example, they may keep farm animals separated from dinosaurs.

Sorting and patterns are related to categorical reasoning. In the same way grocery stores sort out items by their parallel uses, your child will learn how to sort things based on their characteristics and how they are the same or different from other objects.

They’ll sort objects by weight, shape, quantity, texture, color, and other traits, often without even realizing it!

It’s important to note here that sorting and counting aren’t sequential. Your child might begin sorting before they begin counting, in fact.

For instance, if you want your child to sort a bowl of fruit, you can ask them to count all of the strawberries. They’ll sort the strawberries from the rest of the fruit. If you ask them to count the red fruit, they’ll sort out strawberries, cherries, and watermelon and count them together.

Once a child has learned to isolate characteristics, they can begin to identify, extend, and even create patterns. Your child will learn how to:

  • Copy a pattern
  • Identify the parts that repeat and continue a pattern
  • Correct a mistake in a pattern
  • Explain a pattern
  • Create their own patterns

To encourage your child to explore patterns, take a few moments to build a pattern for them when you play together. Use whatever materials you have available and create a simple AB pattern, such as truck, car, truck, car.

Next, point to each object. Say its name aloud. Then, when you get to the end of the row, ask them what comes next. If they aren’t sure, grab the next object and put it down. Once you’ve completed one round, start at the beginning and repeat each item to reinforce the pattern.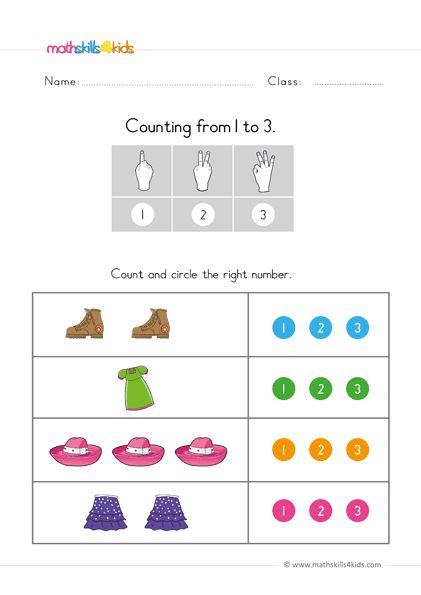

5) The Language Of Math

Part of learning how to do math means learning how to “speak” math. We don’t mean your child will turn into C-3PO — just that they will learn how to use mathematically correct language, or how to tell a story with math terms.

This can happen in daily life. While picking at an afternoon snack, your younger child may say, “Hey! My brother has more crackers than me!” Then you might agree to “add” to the cookies on the younger child’s plate so that both plates are “equal.”

These skills may be naturally exciting for your child — they’ll feel like they’re learning how to speak “grown up!” Show them how fun it is to incorporate mathematically appropriate language into their daily speech and use it to tell stories about what’s going on around them.

Using words to describe things in their lives will help them give ownership over ideas and observations. Motivate them to think about the order of the world around them and use different words to describe them, such as:

  • More than
  • Less than
  • Shape names
  • Light or heavy
  • Small or big

Mastering math language will help them in their quest to become robust mathematicians! It’ll also help them develop a strong vocabulary so they’re better prepared for kindergarten.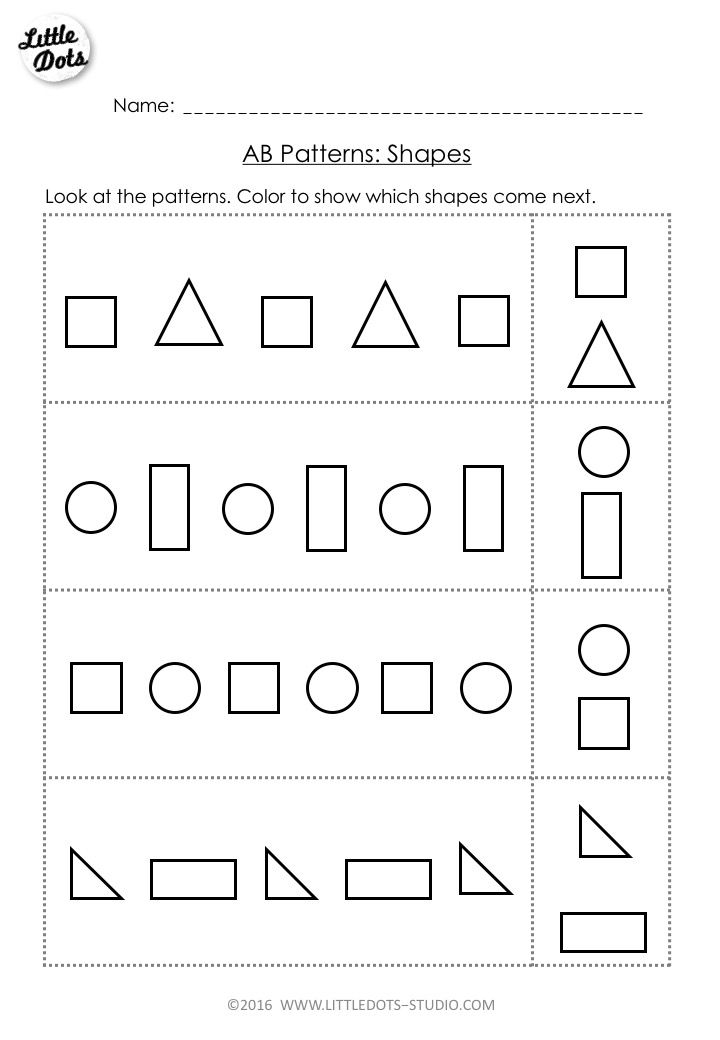

Basic Pre-K Math Checklist

Now that you know some of the concepts your child will be learning in pre-k math, let’s look at some of the skills they’ll build during this time.

  • Rote count to 10
  • Use one-to-one correspondence to count up to 10 objects and tell how many there are altogether
  • Recognize basic shapes (circle, triangle, square)
  • Understand the concept of quantity (more/less)
  • Sort objects by one characteristic
  • Understand and use directional terms, such as up, down, in, out
  • Pick what object goes next in a simple pattern

While these aren’t all of the math skills your child might learn in pre-k, they will give your child a solid mathematical foundation to build on in kindergarten. And they’re all skills you can practice in fun ways!



Pre-K Math Development

As your child grows and learns, they’ll work through three phases of mathematical development: concrete, representational, and abstract.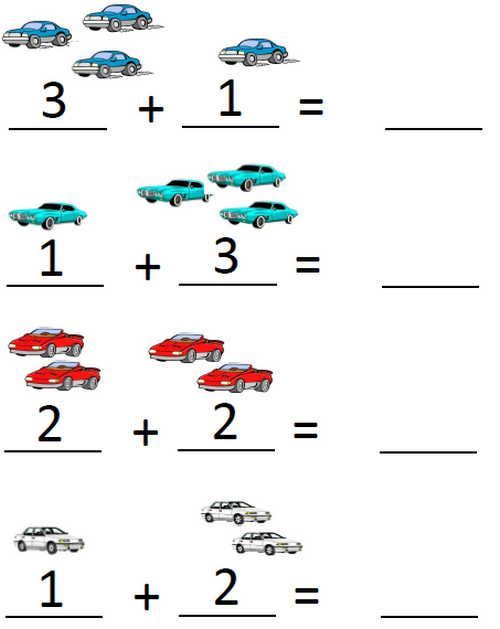 They’ll likely be in the concrete stage at the beginning of pre-k.

During this phase, students need hands-on activities and real-world examples to help them understand mathematical concepts. This is why math manipulatives are so crucial in the early years. It’s also essential to present math concepts in a very concrete way during this stage.

For example, if you’re teaching your child about numbers, don’t just tell them that five is more than three. Instead, show them five objects and three objects, and let them count for themselves. This will help them understand the concept of more and less.

As your child continues to learn and practice a mathematical concept, they can move into the representational phase. Here, students can count pictures or images instead of actual objects. For example, they realize that numbers can be represented by lines or drawings.

Then, they’ll be ready to try the abstract stage. At this point, children understand that numbers can be represented by symbols.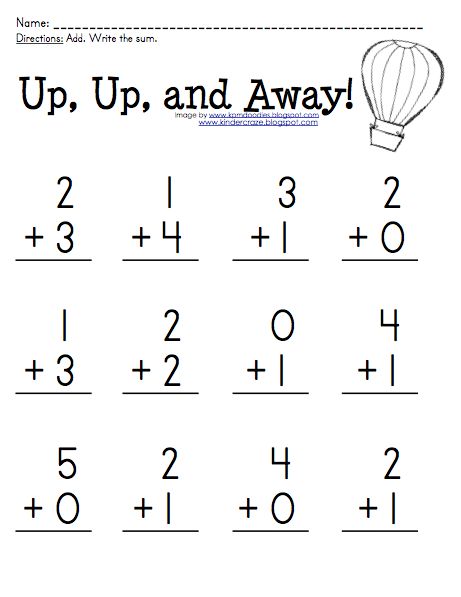 They don’t need manipulatives or visual aids to do math problems. They can start using numbers and symbols such as + or – to solve math problems.

The activities above will help your child to build their understanding of mathematical concepts so they can move through the different stages.

But, in pre-k, it’s important to focus on the process, not the answer. So don’t worry if your child doesn’t get the solution right away. Let them work through the problem and try to figure it out for themselves.

A strong foundation in pre-k math sets children up for success when they start kindergarten. By providing opportunities for them to explore and experiment with math, you can help them develop the skills they need to be successful in school and beyond.

9 Fun Pre-K Math Activities

Now that you’re clear on all of the exciting new math concepts your pre-kindergartener will be exposed to and what skills they’ll practice, let’s talk about some games and activities you can play at home to help your child hone them.

We’ve already discussed some math activities you can incorporate into everyday life. Now, we’re sharing our list of fun games to encourage your young learner to love math even more.

1) What Did I Do?

This game helps reinforce counting, adding, and subtracting. It’s quick to play, so it’s perfect for when you have a few extra minutes.

What You’ll Need
  • Small objects (e.g., paper clips)
What To Do

Place some paper clips (or any other small objects) in your hand, and let your child count how many you have. After they’ve done this, put your hands behind your back and either add or remove some.

Next, show your child the new quantity and ask them to count how many there are now. You can ask your child questions, such as, “Did I add or take away some paper clips?” or “How many did I add or take away?”

For even more fun and learning opportunities, take turns playing the game. And when it’s your turn to guess, it’s OK to guess wrong — “I think you took away 10!… No! I added two!” This back and forth offers lots of laughs and critical thinking for your little mathematician.

Remember that because your child is in pre-k, the concepts of addition and subtraction are still new. Therefore, it’s best to keep the number of objects used in this game low (e.g., 1-10 clips) so they aren’t confused or overwhelmed.

2) Math Tic-Tac-Toe

Add a mathematical twist to the classic game of Tic-Tac-Toe!

What You’ll Need
  • Paper
  • Pencil
  • Ruler
  • Markers (or colored pencils)
What To Do

Start by dividing your sheet of paper into squares by drawing lines (three horizontal by three vertical). In traditional tic-tac-toe, you’d leave these squares blank until the game starts. Not this time.

For this version of the game, you’ll need to fill each box with dots and have your child tell you how many dots are in a box before placing their X or O in it. The first player to get three Xs or Os wins!

The Xs or Os don’t have to be in order at this point, but you can add that requirement as a challenge once your child gets the hang of playing the game.

This activity helps kids work on their counting skills while also incorporating lots of fun.

3) NumberBow

Your child will add numbers to create a beautiful rainbow in this game.

What You’ll Need
  • Two dice
  • Two sheets of paper
  • Colored pencils (or crayons)
  • Pencil
What To Do

Draw two identical rainbow-shaped boards (one on each sheet of paper) with numbered boxes on the rainbows. (You can check out this link for reference.). The aim of the game is to color the numbered boxes in.

To play, each player throws two dice, then adds the numbers from the throw together and colors in the corresponding box on their rainbow.

For example, if your child throws a three and a one, they’d need to add 3+1 and color in the “4” box. If they’ve already colored that box in, they’d have to wait for their next turn. Each player gets 10 turns to have the most colorful rainbow at the end!

While this is an effective game to help your child work on their addition skills, some children might experience difficulty adding larger numbers together (e. g., 5 and 6). If you need to help them, that’s OK!

Remember that exposure and repetition are very beneficial for young learners.

4) Fill The Cup

This game can be challenging for younger children, so if it causes frustration, play other math games until your child is more comfortable with adding and counting.

What You’ll Need
  • Dice
  • Plastic cup
  • Small objects that are easy to count (e.g., paper clips, dried beans, pebbles, etc.)
What To Do

To begin the game, players roll the dice at the same time. The number rolled indicates the number of items you can add to your cup. For example, if you roll a five, you add five dried beans. The goal for your child is to be the first one to fill their cup.

At the pre-kindergarten stage, some children might not be comfortable with the steps needed to play this game (rolling the dice, reading the number aloud, adding the items to the cup). So, before starting, take a few minutes to get them used to the process.

If you notice that it’s still too challenging, you can make it easier by choosing to roll the dice for each other. In this option, you can roll the dice and then help your child read the number and add the right amount of items to their cup.

Whichever variation you choose, this is a fun and engaging way to help children learn numbers and practice counting.

5) Stand Up, Sit Down

Kids enjoy playing this active game where they get to use their bodies and their brains! (Note: This game requires more than one child player, so it’s a great activity for siblings or to do when your child has a friend over.)

What You’ll Need
  • Index cards
  • Marker
What To Do

Write the numbers 1-10 on the index cards (one number per card) and hand three to each participant. Then, say a math equation (or word problem) out loud.

If the answer matches a number they’re holding, the child will stand. If they don’t have the answer, they remain seated.

For example, if the question is, “If I have three dried beans and I throw away one, how many do I have left?”, the child with “2” would then need to stand up and show their card.

The player who has the least number of cards left at the end of five rounds wins. Note: To make it easier, you can give children small items (e.g., blocks, dried beans, paper clips, etc.) to help them count.

Stand Up, Sit Down is also helpful for children learning shapes. Instead of writing numbers on the cards and handing them out, you can draw different 2-D and 3-D shapes that children learn in pre-k (as discussed above) and hand those out.

To play, someone describes a shape and the player who has that shape stands up and says what it is. For example, “If you are holding a shape that has three sides, stand up right now!”

When the child stands up, they’ll need to say that their shape is a triangle, and they get the point. In this version of the game, the player with the most points at the end wins.

Using this game allows children to learn the names and attributes of the different 2-D and 3-D shapes they get exposed to in pre-kindergarten.

6) Who Has More?

This game is perfect for helping kids understand the concepts of more and less, which are critical in early math development.

What You’ll Need
  • A small bowl or container
  • A teaspoon
  • A handful of objects (e.g., buttons, pennies, cereal pieces, etc.)
What To Do

Place the objects in one bowl. Have your child scoop a teaspoon of them out and count them. Then, you do the same and see who got the most. That person’s the winner!

Note: Counting past 10 is difficult at this age, so you’ll want to use big enough items (such as large kidney beans) and stick to a teaspoon for scooping so your child doesn’t end up with more than 10 per spoonful.

7) Read Math Books

Help your child develop a love for math by reading math-related books together.

What You’ll Need
  • A mathematical-themed book to read together (see some recommendations below)
What To Do

Grab one of the following books and snuggle up with your little one for a math-themed storytime.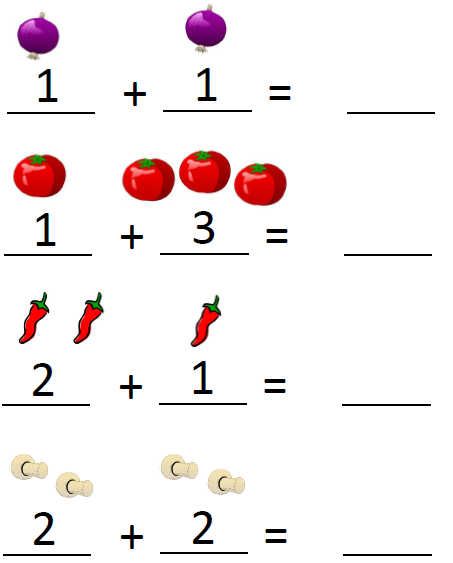 As you read, point out any mathematical concepts in the book.

  • From the Garden by Michael Dahl
  • The Shape of Me and Other Stuff by Dr. Seuss
  • The Button Box by Margarette S. Reid
  • A Pair of Socks by Stuart J. Murphy
  • The Berenstain Bears and the Spooky Old Tree by Stan and Jan Berenstain
  • Pattern Fish by Trudy Harris

When you finish reading, discuss any new math concepts your child learned. You could even do a related activity or two to reinforce what they’ve learned.

8) In The Box

This game helps your child practice prepositions or direction words, like “under,” “behind,” and “in front of.” These concepts are essential for mathematical development as well as reading comprehension.

What You’ll Need
  • A stuffed animal
  • An empty box large enough for the animal to fit inside
What To Do

Ask your child to put the animal inside the box. If they have difficulty understanding what you mean, give them some clues. For example, you could say, “Put the animal in the box so that its head is sticking out,” or “Put the animal in the box so that only its tail is showing.”

Once the animal is in the box, ask them to describe where it is using prepositions. So, they might say, “The animal is in the box.”

Then, take the animal out and place it behind the box. Ask your child to describe its location again. For example, they might say, “The animal is behind the box.”

Next, let them take a turn placing the animal in, on, under, next to, etc. the box. When they’re done, you describe where it is. Continue taking turns as you practice different prepositions.

9) Number Line Race

This game helps kids with number recognition as well as one-to-one correspondence.

What You’ll Need
  • Number cards (we recommend the ones from the HOMER Explore Numbers Kit)
  • A die
What To Do:

Spread the cards out in numerical order, with a bit of space between each one. They should form a line on the floor, though it doesn’t need to be perfectly straight.

Have your child stand on the card with the number one on it. Hand them the die and let them roll it. Call out the number they rolled. Next, ask them to move that many numbers forward, moving from one index card to the next as they count aloud.

If they land on a number that would take them off the end of the line, they start from the beginning for their next throw (each player gets five throws). Then, it’s your turn! Start on one and see how far you can get, too.

The person to end on the card with the highest number is the winner!

Encouraging A Love Of Pre-K Math At Home

Pre-k math isn’t just reserved for pre-k classes. You can help your child explore the exciting world of pre-k math right from your home!

HOMER is always here to help and happy to be your at-home learning partner. Our Learn & Grow app offers tons of opportunities for your child to develop their pre-k math skills from conception to execution.

Our games are personalized to accommodate your child’s specific interests. They include pattern-identification games like Ribbons or shape-building games like the Castle Creator.

Your child can also explore the Shapery Bakery, where they help the cute, cuddly Tisa the Cat by sorting treats based on their shape. All that and so much more can help your child develop their pre-k math skills!

Author

WWC | Pre-K Mathematics

WWC | Pre-K Mathematics

Intervention > Evidence Snapshot

Download Intervention Report 187 KB

Pre-K Mathematics with DLM Early Childhood Express Math was found to have no discernible effects on oral language, print knowledge, and phonological processing and positive effects on math for preschool children.

Pre-K Mathematics is a supplemental curriculum designed to develop informal mathematical knowledge and skills in preschool children. Mathematical content is organized into seven units. Specific mathematical concepts and skills from each unit are taught in the classroom through teacher-guided, small-group activities with concrete manipulatives. Take-home activities with materials that parallel the small-group classroom activities are designed to help parents support their children’s mathematical development at home.


A summary of the effectiveness of an intervention in an outcome domain, based on the quality of research, the statistical significance of findings, the magnitude of findings, and the consistency of findings across studies.

Effectiveness Rating Key

Positive:  strong evidence that intervention had a positive effect on outcomes.

Potentially Positive:  evidence that intervention had a positive effect on outcomes with no overriding contrary evidence.

Mixed:  evidence that intervention’s effect on outcomes is inconsistent.

No Discernible:  no evidence that intervention had an effect on outcomes.

Potentially Negative:  evidence that intervention had a negative effect on outcomes with no overriding contrary evidence.

Negative:  strong evidence that intervention had a negative effect on outcomes.

For more, please see the WWC Glossary entry for rating of effectiveness.

Evidence Tier.

The percent of each characteristic is based on the sample size of all studies meeting standards that reported data on the characteristic.

Percentages below may not add to 100 percent.

Findings

2

studies that met standards out of

4

eligible studies reviewed

Outcome Domain Effectiveness Rating Grades Evidence Tier
General Mathematics Achievement PK
Oral language PK
Phonological processing PK
Print knowledge PK

Last Updated: December 2013

Summary of all Research Settings and Samples that Met Standards

Race

Asian 4%
Black 49%
White 20%
Other or unknown 4%

Ethnicity

Hispanic 23%
Not Hispanic or Latino 77%

Gender

Male: 48%

Female: 52%

Delivery Method

Small Group

Whole Class

Urbanicity

Urban

Locations

NY, CA

Northeast, West

Note: This summary only includes data from studies that reported sample information. The Intervention Report may include evidence from other studies that met standards, but did not report sample information.

Related Resources

This intervention report was prepared for the WWC by Mathematica under contract ED-IES-13-C-0010.

Connect With the WWC

loading

back to top

The best math textbook? Computing is Easy I started reading, and really, it was the simplest book in English that I read (I advise you to try to read it in the original), and I understood it better than in my native language.

But why should adults who know mathematics firsthand read it?

Everything is simple in this matter: probably many already have children or will soon, therefore, it is necessary to instill a love for knowledge and science from an early age, otherwise the school with their stingy language will spoil the child's desire to reach for the beautiful.

But this is not just a book for children. Adults can see if they taught him at school and he didn’t mix anything up because of the long years of business logic planning. Or maybe someone just like me did not know some English terms for mathematics.

It will especially help people who dreamed of becoming hardcore "data-Satanists" and other geniuses of our time, but somehow everything did not work out. For many testers, HRs, project managers who have found themselves in IT, but want to develop further.

The translation is quite free , I'm not a professional translator and I didn't even study at MIT, but I tried to make it as clear and close to the meaning of the text as possible. I will take note of your comments. I translated the test piece to understand if it is interesting for you to get motivated. The first piece belongs to someone who wrote the introductory book, and the second piece belongs to the original author, which is even more interesting and fun. Well, let's fly.

Easy to calculate

Preliminary Chapter 1 WHAT IS A FUNCTION?

No concept in mathematics, especially in calculus[1], is more fundamental than the concept of a function. The term was first used by Gottfried Wilhelm Leibniz in a 1673 letter to the German mathematician and philosopher who invented calculus independently of Isaac Newton. Since then, the term has undergone
gradual expansion of meaning.

In traditional calculus, a function is defined as a relation between two members of [term], called variables because their values ​​differ. Name the terms x and y. If each value of x corresponds to exactly one value of y, then y is said to be a function of x. Usually x is used for what is called the independent variable, and y is used for what is called the dependent variable, because its value depends on the change in the value of x.

As Thompson explains in Chapter 3, letters at the end of the alphabet are traditionally applied to variables, and letters in other parts of the alphabet (usually the first letters such as a,b,c...)
are applied to constants.

Constants are terms of an equation that have a fixed value. For example, in y = ax + b, x and y are variables, but a and b are constants. If y = 2x + 7, the constants are 2 and 7. They stay the same as x and y change.

A simple example of a geometric function is the dependence of the area of ​​a square on the length of its side. In this case, the function is called a single-valued function because the dependence goes both ways. The side of a square is also a function of its area.

The area of ​​a square is the product of the length of its side and itself.

To express the area as a function of the side, we represent y - area, x -
side, we can write:

y \u003d x 2

Of course, x and y are assumed to be positive.

A slightly more complicated example of a single-valued function is the ratio of a side of a square to its diagonal. The diagonal of a square is the hypotenuse of an isosceles right triangle. We know that by the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In this case, the sides are equal.

To express the diagonal as a function of the side of the square: let y be the diagonal, x side, and write as:

y= 2 √(2*x 2 ),

Or more simply:

y=x√2

To express the side as a function of the diagonal, let y be the side, x the diagonal, and write:

y= √(x 2 /2) or more simply: y= (x/√2)

The most common way to name a function is to replace the dependent variable, where f(x)—f would be the first letter of the "function" . So y = f(x) = x 2 means that y, the dependent variable, is the square of x. 9[ explicit] function x. If an equation has the equivalent form 2x - y - 7 = 0, it is called an implicit function of [implicit] x because the explicit form is implied by the equation.

This is easily obtained from the equation by rearranging the terms. Other symbols are often used instead of f(x).

If we want to give numeric x and y values ​​in example
y = f(x) = 2x - 7, we replace x with any value, say 6, and write
y = f(6) = (2 . 6) - 7, which gives the dependent variable y the value 5.

If the dependent variable is a function of one independent variable, the function is said to be a function of one variable. Common examples, all one-to-one functions:

The circumference or area of ​​a circle in relation to its radius.

The surface or volume of a sphere in relation to its radius.

Logarithm of a number in relation to a number.

Sines, cosines, tangents and secants are called trigonometric functions.

Logarithms are logarithmic functions.

Exponential functions are functions where x, the independent variable, is the exponent in the equation, for example, y = 2x. There are, of course, an infinite number of other examples of more complex single variable functions that are given names.

Functions can depend on more than one variable. Again, these examples are endless. The hypotenuse of a right triangle depends on two sides, not necessarily equal. (Of course, this function has three variables, but it's called a two-variable function because it has two independent variables. )

If z is the hypotenuse, we know from the Pythagorean theorem that z = √( x 2 + y 2 )

Remarkably, this is not a single-valued function. Knowing x and y gives z, which is a unique value, but knowing z does not give unique values ​​for x and y.

Two other familiar examples of functions of two variables, the area of ​​a triangle as a function of its height and base, and the area of ​​a right circular cylinder as a function of its radius and height.

Functions of one and two variables are widely used in physics.

The period of a pendulum depends on its length. The distance of the thrown stone, and its speed depends on the time elapsed since it was thrown. Atmospheric pressure is a function of altitude. The energy of a bullet is a function of two variables, depending on its mass and speed. The electrical resistance of a wire depends on the length of the wire and the diameter of its round section.

Functions can have any number of independent variables. A simple example of a function of three variables is the volume of a rectangular room. It depends on the two sides of the room and its height. The volume of a four-dimensional hyperroom is a function of four variables.

The novice math student should know how equations with two variables can be modeled by curves on the Cartesian (Cartesian) plane. (The plane is named after French mathematician and philosopher René Descartes, who invented it.)

The independent variable is represented by points along the horizontal x-axis. Dependent variable values ​​are represented by dots along the vertical y-axis. Points on the plane represent an ordered pair of numbers x and y. If the function is linear, that is, if it has one form y = ax + b, then the curve representing the ordered pairs is a straight line. If the function is not of the form ax + b, then the curve is not a straight line.

Figure 1. y=x2 or f(x)=x2

Note that the scales are different on the two axes.

Figure 1 is a Cartesian plot y = x 2

The curve is a parabola.

The dots along each axis represent real numbers (rational and irrational), positive to the right of the x-axis, negative to the left, positive to the top of the y-axis, negative to the bottom.

The starting point of the graph where the axes intersect is zero. If x is the side of a square, we assume that it is non-zero and non-negative, so the corresponding curve will only be the right side of the parabola.

Suppose the side of the square is 3. Move vertically up from 3 on the x-axis to the curve, then go left to the y-axis, where you will find that square 3 is 9. hat").

If the function includes three independent variables, the Cartesian plot must be extended to three dimensions with x, y and z axes.

I once heard about a professor whose name I don't know, remember longer, who liked to dramatize about this space for his students, running back and forth, he exclaimed: "This is the X axis!". He then ran up and down the center aisle, yelling, "It's the Y-axis!" and finally jumped up and down, yelling, "It's the z-axis!". 0007

Functions with more than three variables require a Cartesian space with more than three axes. Unfortunately, the professor could not dramatize the axes above three, only by running or jumping.

Note the labels "domain" and "range" in Figure 1. In recent decades it has become fashionable to generalize the definition of a function. The values ​​that an independent variable can take on are called the domain of the variable. The values ​​that a dependent variable can take is called a range. On a Cartesian plane, a domain consists of numbers along the horizontal (x) axis, a range consists of numbers along the vertical (y) axis.

Domains and ranges can be infinite sets, such as the set of real numbers or the set of integers; or any of them may be a finite set, such as a fraction of the real numbers.

The numbers on a thermometer, for example, represent a finite range of real numbers. If used to measure the temperature of water, the numbers indicate the interval between the freezing and boiling points of water. Here, the height of the mercury column relative to the temperature of the water is a one-to-one function of one variable.

In modern set theory, this way of defining a function can be extended to completely arbitrary sets of numbers for a function that is described not by an equation, but by a set of rules. The easiest way to specify rules is with a table.

Figure 2. Arbitrary function

For example, In fig. 2 shows a table with a set of arbitrary numbers that make up the domain on the left. The corresponding set of arbitrary [arbitary] numbers is in the range on the right. The rules governing this feature are indicated by arrows. These arrows show that each number in the domain corresponds to one number on the right. As you can see, more than one number on the left can lead to the same number on the right, but not vice versa.

Another such example is shown in fig. 3 along with a plot consisting of 6 isolated points on a plane.

Since each number on the left leads to exactly one number on the right, we can say that the numbers on the right are a function of those on the left. Some authors say that the numbers on the right are “correct images” of those on the left. [here is a pun]

Arrows are said to provide a “mapping” of a domain to a range. Some call the arrows “mapping rules” that define function

Figure 3. How [graphed - can also be translated “represented as a graph”] is another arbitrary discrete function of integers.

For most functions encountered in calculus, the domain of definition consists of one interval of real numbers. The area can be the entire x-axis, as is the case for the function y = x 2.

Or it can be an interval limited, for example, by the domain of y = arcsin x.

Which consists of all x such that -1 < x < 1.

Or it can be limited on one side and unlimited on the other side; for example, the domain of definition y = √(x), consists of all x > 0.

We call such a function continuous if its graph can be drawn without lifting the pencil from the paper, and “discontinuous” otherwise. (A full definition of continuity, which also applies to functions with more complex domains, is outside the scope of this book.)

Figure 4. This function is called the largest integer function because it is
maps each real number (on the x-axis) to the largest integer on the y-axis equal to or less than the real number.

For example, all three functions just mentioned are continuous. On fig. 4 shows an example of a discontinuous function.

Its domain consists of all real numbers, but its graph [graph, diagram, pattern] has infinitely many parts that are not related to each other.

In this book, we will deal almost entirely with continuous functions.

Note that if the vertical line from the x-axis intersects more than one point on the curve, the curve cannot represent the function because it maps x to more than one y.

Figure 5 is a graph that is clearly not a function because vertical lines, such as the one shown by the dotted line, cross the graph at three points. (It should be noted that Thompson did not use the modern definition of "function". For example, the graph shown in Figure 30 in Chapter XI fails the vertical line test, but Thompson thinks it is a function.)

Figure 5. Graph that does not express a function.

In this generalized function definition, a one-variable function is any set of ordered pairs of numbers such that each number in one set is related to exactly one number in the other set.

In other words, in ordered pairs, no number x can repeat, although a number y can.

Representing functions in this way, we will consider arbitrary combinations of a safe or a sequence of buttons to be pressed to open a door as counting functions. To open the safe, you must turn the handle back and forth to get a random set of integers. If the combination is safe, say 2-19-3-2-19, then these numbers must be obtained to open the safe, or the order in which you need to press the buttons.

In this way, the heights of the tiny "peaks" of the cylinder lock's key lobe are an arbitrary function of positions along the length of the key.

In recent years, mathematicians have expanded the notion of a function to even include things that are not numbers. Indeed, they can be anything that is an element of a set. A feature is simply the ratio of each element in one set to exactly one element in another set. This leads to all kinds of uses of the word function that seem absurd.

If Smith has red hair, Jones has black hair, and Robinson has white hair, the hair color is a function of the three men. The positions of cities on the map are a function of their position on the ground. The number of fingers in a standard family is a function of the number of people in the family. Different people can have the same mother, but no one can have more than one mother. This allows us to say that mothers are a function of people.

Elephant mothers are a function of elephants, but not grandmothers, because an elephant can have two grandmothers. As one mathematician recently put it, functions have been generalized "to the heavens and down to the earth. "

A useful way to think of functions in this general way is to think of a black box with inlets and outlets. Any element in the domain, numbers or whatever, is placed in the field. Outside pushes one element in some range. The mechanics inside the box magically provide correlations using whatever matching rules govern its function. In calculus, the inputs and outputs are almost always real numbers, and the mechanism in the black box works according to the rules given by the equations.

Since the generalized definition of a function leads to strange extremes, many teachers today, especially those who have an engineering background, find it confusing and unnecessary for students to introduce such a broad definition of functions at the beginning of the calculus, however, an increasing number of modern calculus textbooks spend many pages on a generalized definition. Their authors believe that defining a function as a mapping of elements from any set to any other set is a strong unifying concept that should be taught to all mathematics students.

Opponents of this practice believe that the calculus should not touch the toes, cities, mothers and elephants. Its domains and ranges must be limited, as they have always been, to real numbers whose functions describe continuous change.
It's a fortunate and surprising fact that the basic laws of our fantastical bustling universe are based on relatively simple equations. If it were otherwise, we would certainly know less than we now know how our universe behaves, and Newton and Leibniz would probably never have invented (or discovered?) calculus.

[1] Calculus is a branch of mathematics dealing with finding and properties of derivatives and integrals of functions by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.

Prologue.

Considering how many fools can do calculations, it's amazing that this is an unthinkably difficult or tedious task for any other fool who is trying to learn how to master the same tricks.

Some computational tricks are quite easy. Some of them are extremely difficult.

Fools who write advanced math textbooks - and they are mostly smart fools - rarely bother to show you how easy simple calculations are. On the contrary, they seem to want to impress you with their great dexterity, while going through the most difficult path.

Being a wonderfully stupid fellow, I have had to wean myself from these difficulties, and now is the time to leave chapters to my foolish colleagues that are not so difficult to understand. Master them carefully, and the rest will follow. For what one fool can do, another can do.

***

CHAPTER I. Your deliverance from the initial torment

The first horror, from which most graduates suffocate, without even trying their hand at calculations, can be discarded once and for all - one has only to show them what they mean with common sense point of view, the two main symbols that are used in the calculation.

Those awful symbols are:

(1) d which just means "a little".

So dx means a little x; Or du means a little u.

Nerd mathematicians find it more polite to say "element" instead of "a little". As you please.

But you will see that these small sets (or elements) can be considered infinitesimal.

(2) ∫ which is just a long S and can be called (if you like) "the sum",

thus

∫dx means the sum of all the small parts of x;

or ∫ dt means the sum of all small parts of t.

Ordinary mathematicians call this symbol the "integral of". Now any fool can see that if you imagine that the number x is assembled from many small parts, each of which is called dx, then if you

add them together, you get the sum of all dx's (which is the same as the whole x). The word "integral" simply means "the whole."

If you think of the length of time in one hour, you can (if you like) think that it is made up of 3600 little pieces called seconds. All 3600 pieces added together make up one hour.

When you see an expression that begins with that dreadful symbol, you will henceforth know that it is only there to give you instructions on how to perform the operation (if possible) to sum up all the little parts denoted by these symbols.

That's all.

CHAPTER II.

VARIOUS POWERS OF SMALL

We will see that in our calculations we are dealing with a small number of different powers of small.

We will also need to know under what circumstances we can consider small quantities so small that we can discard them from consideration. It all depends on the relative detail [minuteness].

Before we lay down any rules, let's think about familiar cases.

So 60 minutes is an hour, 24 hours is a day, 7 days is a week.

Therefore, there are 1440 minutes per day and 10080 minutes per week.

Obviously, 1 minute is a very small amount of time compared to a whole week.

Indeed, our ancestors considered it fleeting in comparison with an hour and called it "one minute", [one minute] meaning "a fraction of a minute", namely, one sixtieth of an hour.

When it came time to create even smaller divisions, each minute was divided into another 60 parts, which in the time of Queen Elizabeth were called "second minutes" [second minutes] (that is, small amounts of the second order of smallness).

These days we call these second orders small - "seconds". But few people know why they are called that.

Now, if one minute is so small compared to a whole day, how small is a second?!

Again, think of a farthing versus a sovereign (names for copper and gold English coins): the difference is much more than 1/1000. The farthing has a relatively small denomination compared to the sovereign: it can certainly be considered as a small amount.

But compare a farthing to 1,000 pounds: this is a relatively large amount in which a farthing has a value of no more than 1/1000, as is the case with a sovereign and a farthing. Even a gold sovereign makes up a relatively insignificant amount in the wealth of a millionaire.

Now, if we fix any numerical fraction as a constituent proportion, which for any purpose we call relatively small, we can easily indicate other fractions of a higher power of small.

Thus, if our goal is time, then 1/60 is a small fraction, and 1/60 of 1/60 is a small fraction of a small fraction (fraction [fraction] or division), which can be considered as a small amount of the second order of smallness. *1

Or, if for any purpose we take 1 for every cent [per cent] (i.e. 1/100) as a small fraction, then 1% of 1% (1/10,000), then this will be a division of the second order of smallness; And 1/1,000,000 will be part of the third order of smallness, and so on.

Finally, suppose that for some very precise purpose, we have to treat 1/1,000,000 as "small". Thus, if a first-class chronometer does not lose or gain more than half a minute in a year, it must keep time to within 1 error every 1,051,200 moves.

Now, if for this purpose we count 1/1,000,000 (or one millionth) as a small amount, then 1/1,000,000 1/1,000,000, that is 1/1,000,000,000,000 (or one billionth) will be a small amount of the second order of smallness and may be completely ignored in comparison.

*

Then we see that the smaller the small value, the more negligible the corresponding second-order quantity became.

From this we know that in all cases we confine ourselves to neglecting a small amount - of the second or third (or higher) - order, if only we accept a small quantity of the first order as sufficient.

But, it must be remembered that small quantities, if they appear in our expressions as factors multiplied by some other coefficient, can become important if the other coefficient is itself large. Even a farthing becomes important if only it is multiplied by a few hundred.

*

Now in calculus we write dx for the part of x. Things like dx, du, and dy are called "differentials" - a differential from x, or from u, or from y, as the case may be. [You read them as "De-X", "De-Yu" and "De-Vai"] 92 is negligible only if we consider incrementing dx to itself a sufficiently small number of times.

Let's look at the comparison.

*

Now if Mr. Millionaire gets £1,000 in the next week, the secretary will get £10 and the boy 2 shillings.

Ten pounds is a small amount compared to £1000; But two shillings is extremely small, indeed, has a very secondary order.

But what would be the disproportion if this share, instead of 1/100, was calculated at the level of 1/1000 part? Then, while Mr. Millionaire got £1,000, Mr. Secretary would only get £1, and the boy would get less than one farthing!

*

Witty D. Swift once wrote:

Parasites always bite, They differ by barely an inch.

Apparently it happens endlessly,

For the naturalist keeps the gold of doom:

"A flock of fleas sits on every back of the head and back.

Here you are, here is a cat, here is God - in this sense, no one is bad. "

The cat can take care of a regular sized flea - a small creature. First order of smallness.

But, probably, he would not bother himself, looking for fleas in a flea - being of the second order of smallness, which would be insignificant for him. Even a large number of cat could be neglected.

*

[1] Mathematicians talk about the second order of "magnitude" (that is, greatness) when they really indicate the second order of smallness. It's very confusing

beginners.

[2] "Poetry: Rhapsody" (p. 20), printed 1733 - usually misquoted.

[The translation was made by me, the meaning was conveyed]

Rosobrnadzor summed up the preliminary results of the Unified State Examination in social science

Unified State Examination

June 21, 2022 Moscow Unified State Exam

The Federal Service for Supervision in Education and Science has summed up the preliminary results of the unified state exam in social science, which passed 9June 2022, the press service of Rosobrnadzor reports.

The total number of participants in the main day of the exam exceeded 276,000 people. The average score on the Unified State Examination in Social Studies in 2022 was 59.88. More than 227 thousand participants in the Unified State Examination 2022 in social studies showed a result that exceeded the minimum score for admission to universities. 346 people received the maximum 100 points on the Unified State Examination in social studies.

It is noted that in comparison with previous years in 2022, the proportion of USE participants who have a basic understanding of the social sciences (primarily sociology and political science) has increased. Most of the participants in the 2022 exam were able to correctly find the required information contained in the text, diagram and graph; successfully applied social science knowledge in the process of solving practice-oriented problems. In addition, the rejection of mini-essays allowed students to shift the focus in preparation, concentrating more on mastering the necessary skills and knowledge instead of memorizing ready-made mini-essays.

Learn more