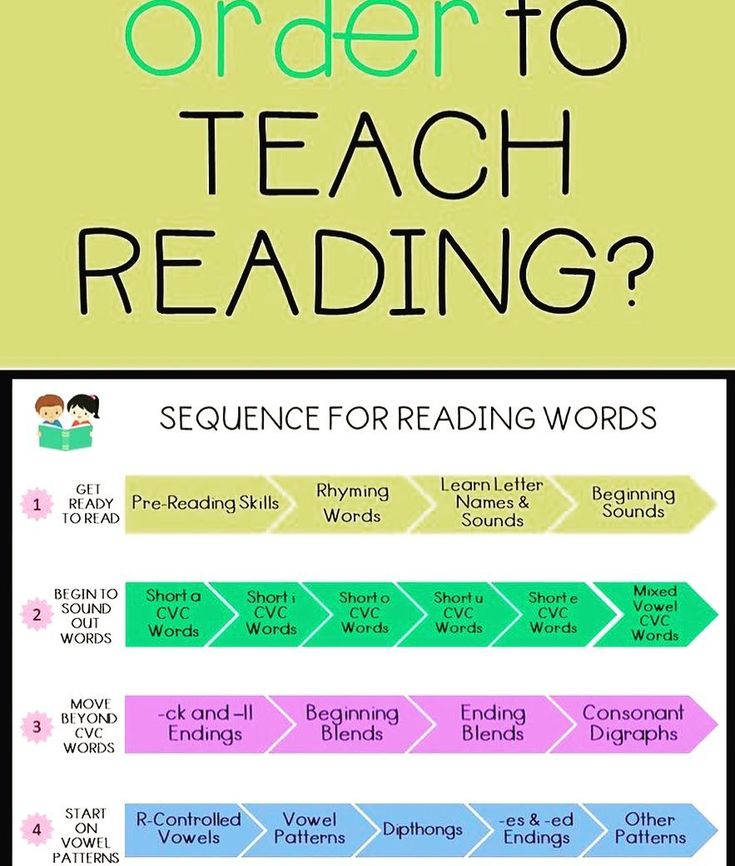
Teaching number recognition

Number Recognition – The Best 16 Games To Teach It (+ Tips) – Early Impact Learning

In the ten years I have spent teaching young children between the ages of 3 to 5, one of the most important secrets I have discovered is how to teach recognizing numbers.

Some children will just pick this up from exposure to numbers in their environment. However, for most children this a long process, and needs some real expertise and strategies to get them confidently recognizing numbers. This is where this article comes in!

So, for the short answer, how do you teach children to recognize numbers?

Teach children to recognize numbers by using fun stories or chants for each number. Practise sky-writing the number in air, drawing it in foam or other messy play substances, and by making numbers in craft activities. Seeing numbers throughout their play is crucial.

That’s the simple version, but there is just so much more to it than that!

In this article I have condensed ten years of trial and error into 17 tried and tested strategies that you really should try to get children recognizing numbers.

Pretty much all of these games can be used either at school or nursery, or at home. Good luck!

1.Use Stories For Each Number

A great way to introduce stories to start with is with storytelling.

Stories are great for teaching lots of different skills, as stories really tap into children’s sense of curiosity and attention like few other things.

One way to do it is have a bag of a few objects. If you are introducing number 3, for example, you could say something like ‘This is number 3. Today it went on an adventure. It found 3 magic stones.’ (Take them out of the bag). ‘It rubbed the stones, and out popped 3 frogs.’ (Take the toy frogs out of the bag).

It is good to spend time during the story looking at what the numeral looks like, and getting them to draw it in the air, or on their hand.

2. Number Stones

Beautiful materials help in the teaching of anything, and these number stones are certainly a fantastic natural resource.

All you need for these are some pebbles. I happened to find some excellent white, sparkly stones by chance, that the children really love.

The idea is to write or paint some numbers on some of the stones. There are other things you can do, like create stones with quantities on as well. For example, I have created these stones with different numbers of bugs on:

These stones are great for some of the following things:

• Finding objects, such as 3 pine cones, and matching to the right numeral

• Match numeral stones to quantity stones, e.g. 4 bugs to the number 4

• Trying to copy a number line and put them in order.

This activity is just one of many exciting ways to use stones and pebbles for learning. To find out a whole load more, you can check out this definitive guide on how to use story stones.

3.Use Chants

There are little fun ditties and chants you can use for each number.

For example, number 3 is:

A curl for you, and a curl for me

That’s how you make number three! I have used chants that I just found on the internet before. For example, this video has some excellent ones you can use:

Also, children really love this song when it comes to numeral formation:

4.Have Number Actions

Many children learn letters through actions when they do phonics, so why wouldn’t the process work for numbers.

The good news is – it does work!

Multisensory learning is definitely the way to go when you are teaching things like recognizing numerals or sounds. It activates a lot more of the brain if you have movements, sound and visuals all mixed together.

The number actions I use I have just invented. They go like this:

0 – Make a circle with your fingers

1 – Throw one arm straight up

2 – Two arms up

3 – These are like Mickey Mouse ears on their side. Put your head to one side, and put Mickey Mouse ears on top (honestly the sideways ears do look like mouse ears)

4 – I get them to cup both hands round their mouths and call ‘Four!’ This is like when a golfer loses their ball and calls ‘fore!’

5 – Show five fingers

6 – Put two fingers up high in the air. This is the signal in cricket for a ‘six’. Apologies to my American friends that I know read this blog in droves! If you have no idea what this means, please feel free to invent your own action for six.

7 – Do a salute with your hand. Your arm will have made the shape of a ‘seven’.

8 – Pretend to hold two apples, one on top of the other. Put them to your mouth and say ‘eight’ (as though you just ‘ate’ the apples)

9 – Put your hand vertically underneath your head with your fingers on your chin. It looks like your head is on your arm, like a lollipop. I looks a bit like a nine – a stick and a circle

10 – Two sets of hands thrown forwards (with ten fingers)

Using actions such as this works a treat for teaching numbers, and is also an excellent way to teach phonemes (sounds) as well.

5.Skywrite Numbers

Skywriting is another great multisensory experience.

It is good if you can show them what the numbers look like on something – maybe a chalkboard, interactive board, or written on big pieces of paper.

The simplest way of skywriting is to stand up, and use your finger in the air to draw the numbers. Make them as big as you can! (i.e. get the children to bend their knees, and stretch up high respectively)

You can make the experience even more exciting by:

• Using ribbons or streamers to draw the numbers in the air

• Skywrite to music!

• Use puppets or toys in their hands to write with

6.

Books are another route to firing up children’s curiosity and interest.

The idea of this strategy is that you find opportunities in books to count or find numbers, and then talk about it. You can write the numbers that you find, or link one of the other strategies in this article to the numbers (for example, skywriting the numbers that you find).

There are a mixture of books you can use:

• Many books are clearly about maths, and they have lots of numerals in anyway. These work really well.

• Some books are nothing to do with counting, but you can link numbers to them anyway. You can count the dwarves in Snow White for example, and write the number. You can count the dogs in Hairy Maclary.

7.Loose Parts On Numbers

Decorating numbers, and turning the numerals into fun art activities is a great way to go to get children recognizing them.

One way is to use loose parts to experiment with the formation of numbers.

All you need to do is create some big numbers somewhere, and the children put lots of loose parts like bottle tops or gems and other things over the top of them to make the shapes of the numbers.

You could:

• Draw numbers on big paper

• Chalk them on the floor outside

• Have big wooden numbers

Good loose parts include things like shells, stones, screws, wood slices, pegs, pompoms, and whatever else you can find. If you are looking for ideas of what other materials you can use for loose parts, then I have written an article containing at least 100 ideas, that you can check out here.

8.Number Lines

Number lines are great for children to start to visualize what numbers look like in a sequence. They are also great for number recognition.

Some excellent ways to use them for this purpose include:

• Making number lines in artistic ways. The children can decorate them, or stick numbers onto sticks or something similar

• They can order numbers on a blank line, copying a number line

• Refer to number lines as you sing songs, or do chants. The more they use them the better they will get.

9.Matching Games

Some old-school memory games are great for number recognition. For example, pairs. Have two sets of number cards. I would just focus on the numbers that you are trying to teach, so it could be numbers 1-5 or 0-10.

Place the pairs of cards down, and take it in turns to turn over two and try to find pairs.

Another game that is similar is number bingo.

Matching games like this are quite simply excellent for memory in general. If you want to find out the definitive list of the best preschool memory games for children, then check this out.

10. Number Golf

They really love this one! Many children really enjoy sports, and so if you can tap into this interest then go for it!

There are different ways of doing this, but one easy way is to use big paper. Draw big circles all over the paper – these are the golf holes. Write numbers in these golf holes.

Then all you need is a golf club and a ball. I normally use a small playdough ball that you roll yourself, and the club can be something like a lolly (popsicle) stick.

Hit the ball around the golf-course and try to get it into the holes. This is great for number recognition. You can also:

• Go in order like a real golf course

• Recognize numbers beyond ten

• Try a big outdoor version using large rubber balls and huge circles drawn with chalks. You could kick or roll the balls

Playdough games like this are brilliant for fine motor.

11. Messy Number Formation

The messier numbers can get the better!

The idea is here is to get some kind of messy surface that the children can mark-make numbers on.

You could use:

1. Shaving foam
2. Shaving gel
3. Porridge oats
4. Glitter (if you’re feeling brave as this will be very messy!)
5. Flour
6. Sand

Have some big numbers for them somewhere to look at and copy. The children try writing the numbers in the messy substance! Hours of fun.

12. Put Numbers On Construction Toys

Another good strategy to teach numbers is to find out what the children enjoy doing anyway, and just add some numbers to these activities.

A good example is construction toys. Lots of children love using lego and building blocks, and lots of other things like this. Why not add some numbers to these resources?

For example, you can write some numbers on some old building blocks. Can they put them in order?

Can they build numbers out of construction toys?

Can they make a tower using a quantity of blocks that matches a number card?

Tapping into interests is one of the key ways of motivating young children. If you want to find out the definitive list of things you can do to focus pre-schoolers then take a look at this article I wrote about the 15 top strategies.

13. Numbers On Vehicles

Vehicles are another thing that many young children are fascinated by. These offer many opportunities, including:

• Make a car-park. Get a large piece of cardboard or paper, and draw some car park spaces on it with numbers on. If the cars have numbers on anyway, even better! You can match the numbers

• Have races and put the winners on a podium of some description, labelled 1, 2 and 3

• Put vehicles with numbers on in order, maybe following a number line

14. Numbers In Environment

This is a really important way that many children will learn numbers – encountering them in the environment.

There are many things you can do to help the process:

• Point out numbers that you or children may find in the environment, and talk about them. Examples could be numbers on doors or bins, numbers on football shirts, numbers on signs

• Encourage children to count and record in the activities that they do. For example, build a tower and count the blocks. Make a model of an alien and count the arms.

• Include numbers in displays around the room

15. Number Dice Games

Competitions and games with dice really help children to learn now to recognize numbers.

The repetition of seeing numbers again and again really helps, and also a little bit of competition really focusses the minds for some.

Some great games to do with a numeral dice include:

• Roll the number dice and do that number of actions – e.g. clap, jump, hop etc

• Have a simple racetrack drawn on the floor. This could be with chalk outside, or something similar. Have a long line of about ten sections in a line, so that it looks a bit like a ladder. All children start at one end. One rolls the dice and then jumps forward that number of squares. Then the next person goes. It is a race to take it in turns, and get to the end first! There are lots of fantastic outdoor maths games such as this one. Check out 50 of the best ideas here!

• Whack the dough! This is a fantastic playdough game that they really love. What you quite simply do, is first make lots and lots of little balls of playdough. Then you roll the dice and whack that number of balls! This is great for number recognition, and 1:1 counting. Playdough is one of the most exciting resources you can use for early Maths. If you want to learn more playdough maths games, then check these out.

16. Fishing Game

This is a simple adult-led game that they really enjoy.

Get some kind of number cards, and stick a big paperclip to the top. Get a stick such as a broomstick, and tie a string to it. At the end of the string have a magnet tied on.

The idea is to have the number cards in the middle of a circle of children all faced down. One child goes first, and tries to pick up a card with the magnet. Hopefully the magnet will be strong enough. If you are having problems picking them up, then stick more paperclips on the cards!

Fish for a card and then identify what it is!

This is one of the favorite games in my book 101 Circle Time Games…That Actually Work!

This book contains:

-All the best math circle time games

-Phonics and literacy circle time games

-Emotion and mindfulness circle time games

-Active and PE circle time games

-And so much more!

You can check out 101 Circle Time Games…That Actually Work here.

Right, that’s the end of the 16 best games I know to teach recognizing numbers. I’m going to finish with some key questions that many people ask about recognizing numbers.

Common Number Recognition Questions Answered

Why is it important to know number names?

Recognizing numbers is a foundation skill of early maths. It is important to develop before you can go on to many other skills.

Some examples of skills that cannot be attempted without first recognizing numbers includes:

• Ordering numbers in any way

• Finding missing numbers in a sequence

• Being able to add and subtract with written number sentences

How to teach numbers to special needs children?

Many of the same strategies will apply if you are trying to teach numbers to special needs children.

Try to make the strategies as multi-sensory as possible. Actions and physical movement is good to support number recognition.

Please bear in mind that the age and speed with which children will learn numbers will vary greatly if they have any disabilities.

Some children, for example with autism, may learn numbers at a very young age, and number recognition can be an exceptional skill of many autistic children.

At what age should children recognize numbers?

This is a tricky question and really will differ for different children.

In general, children will begin to learn how to recognize numbers somewhere between the age of 2 and 5. It is hard to be more precise than that!

Just because a child learns numbers later than another does not mean that their rate of progress will be slower in the future. It is more an issue of child development rather than an indicator of intelligence.

When are children ready to recognize numbers?

Normally children will display some signs before they start to recognize numbers. These include:

• An interest in numbers in the environment

• They are starting to rote count (or indeed are already good at this skill)

• They are beginning to count objects

Do you teach letters in the same way as numbers?

There are definitely parallels between strategies that work well for both. These include:

• Make it multisensory – the more active and fun the process the more chance they have of learning them

• Use songs, chants and books to help the process

• Repeat and practise what you have learned

Find out more about how letters and sounds are taught here.

Conclusion

The more multisensory you can make number recognition learning the better. Spark children’s curiosity with exciting resources, and get them dancing, moving and singing, and the process becomes fun and effective. Good luck, teaching those numbers!

If you liked this article, then why not try one of these:

• What Is Rote Counting? And How To Teach It
• Symmetry Activities For Kids – 10 Fantastic Activities

Recent Posts

13 Hands-On Number Recognition Games Preschoolers will Love

• Share
• Email

Are you teaching your child to identify numbers? Here are some fun and interactive number recognition games for preschoolers and kindergarteners that you can play at home or in the classroom too.

If you’re wondering how to teach number recognition, the answer in early childhood is always through play.

Play is the natural way in which children learn. During play, children practice their skills and make sense of new knowledge and experiences. They develop early maths skills through play.

Remember that there are many aspects to learning about numbers. There is learning to count, which you can teach with games and counting songs, and then there’s one-to-one correspondence, which is when a child reliably counts one object at a time.

Number recognition is about the physical appearance and shape of a number, as well as what value it represents.

These number recognition activities for preschoolers are a great place to start teaching the numbers from 1 to 10, but once you get going you’ll quickly notice opportunities all around you!

This numbers game can be adapted to suit your child’s age, stage and interests.

Write numbers onto some toy cars and create a parking garage with numbered spaces. Your child can then match the number on the car with the number in the space and park the car correctly.

If he needs more of a challenge replace the numerals with dots or words so that your child can begin to recognise numbers being represented pictorially.

If your child is not particularly interested in cars you could do a similar game with animals, dolls, or whatever it is that your child enjoys playing with.

Put numbers on toy cars, or for a large scale activity; bikes and scooters. Create a car wash for them with clothes, brushes, water and bubbles.

Your child is then in charge of ensuring that the cars, bikes, or scooters come to the car wash and get cleaned in the correct order. As well as recognising numerals, this activity gives your child the chance to begin learning about number order.

This fairground classic is great for numeral recognition. How you set this up is your choice.

If you have lots of ducks and something to hook them with then perhaps you could create a replica of the fairground game, otherwise feel free to improvise with what you have at hand.

A net or bowl to scoop objects out of the bath could work well – the important thing is for your child to be having fun and looking at numbers. You could allocate prizes to certain numbers if you want to.

Sidewalk chalk is brilliant for larger-scale mark-making and games that get children using their gross motor skills.

Use sidewalk chalk to write out large numerals, then give your child a paintbrush and a pot of water and have them paint over the numerals with water to erase them.

Not only does this help your child to recognise numerals but also helps with the beginnings of formation.

Create a chart using beads and pipe cleaners. Attach 10 pipe cleaners to a piece of card and write numbers 1-10, one number above each pipe cleaner. Provide your child with a pot of beads and help them to count out the correct number onto each pipe cleaner.

This activity gives your child the opportunity to practice numeral recognition, counting, and assigning the correct value to each numeral. It’s also brilliant for their fine motor skills!

Label some buckets or baskets with numbers and provide your child with beanbags. Have your child step back from the buckets and take aim and throw the bean bags in.

You can do quite a lot with this activity depending on your child’s age, stage and needs, but on the most basic level, it encourages number recognition along with introducing the concept of more and less.

If your child is ready then you can model addition and play to win.

Label pots with numerals and provide counters, craft beads, pom poms or really whatever you have at hand and encourage your child to fill each pot with the correct number of items.

Again, this activity targets a variety of different skills as children recognise numerals, apply their understanding of value, and count out the correct number of items. Another good one for fine motor skills!

Children love to learn outdoors and on a large scale. Many teachers love using small number lines in the classroom to introduce the ideas of one more and one less but you can do the same outside.

Perhaps use chalk to draw out your number line and encourage your child to locate different numerals – “Stand on number 8,” “Hop to number 4” and so on.

If appropriate you could discuss one more and one less. You could also use the number line to encourage counting by inviting your child to find 1 item to place next to the number 1, 2 items to place next to the number 2 and so on.

If your child likes to be creative and artistic then this could work for her. Use nature to create the shapes of numbers.

This might mean drawing in the mud or sand, arranging leaves or stones or even noticing natural shapes in the environment. You could do this in your backyard or take a special walk.

Even better if you can take photos of your creations for your child to look back on. This allows your child to begin thinking about how numerals are formed in a fun and creative way.

Hopscotch is a real playground classic and it brings together a whole host of skills including gross motor skills.

Draw out a hopscotch grid and teach your child how to play, throwing a stone or stick to find out where he needs to hop to, and then hopping and jumping to the end.

As well as reinforcing the recognition of numerals this also introduces the idea of higher and lower and allows your child to have fun while working with numbers.

Hopscotch is my favourite number activity for preschool kids!

11. Potion Recipes

If you like messy, creative play then this one’s for you!

Create a couple of ‘recipe cards’ using measurements expressed as numerals, for example – 2 cups of water, 3 pinecones and have your child follow the recipe card, combining everything together in a big cauldron-like tub.

This taps into children’s imaginations and introduces the concept of measurement as well as number. Once your child is finished following the recipes you have provided perhaps he will be ready to create his own recipes, which you can scribe for him.

All you need is a nice big roll of paper with numbers on and a fly swat dipped in paint. You call out the numbers and your child must swat them, thereby covering them in paint! This is a really fun preschool number activity.

You can play just as easily without the paint, simply swatting at the numerals, but it’s far less fun than making a mess. 

This activity is extremely physical helping to really embed the learning, and as your child tries to speed up, her ability to recognise numerals will improve too so that she’ll soon be able to recognise them at a glance.

Bingo is a great maths game for building up number awareness and can be enjoyed as a family. To start off with you can simply use numerals up to ten but as your child’s knowledge expands so can your game.

You can use what you have on hand – a bowl and folded up pieces of paper, with highlighters – or you can go ahead and buy bingo pads and dabbers and bingo balls to add to the overall experience.

Here you will be building number recognition and as your child aims to increase their speed, she will get quicker and quicker at recognising numbers and linking them to the number names being called out!

I hope you’ll enjoy trying out these number recognition games with your preschooler! Here are some more fun math activities for preschoolers to build early mathematical skills.

Get FREE access to Printable Puzzles, Stories, Activity Packs and more!

Join Empowered Parents + and you’ll receive a downloadable set of printable puzzles, games and short stories, as well as the Learning Through Play Activity Pack which includes an entire year of activities for 3 to 6-year-olds.
Access is free forever.

Signing up for a free Grow account is fast and easy and will allow you to bookmark articles to read later, on this website as well as many websites worldwide that use Grow.

• Share
• Email

A visual introduction to neural networks using the example of digit recognition

With the help of many animations, a visual introduction to the learning process of a neural network is given using the example of a digit recognition task and a perceptron model.

Articles on the topic of what artificial intelligence is have been written for a long time. And here is the mathematical side of the coin :)

We continue the series of first-class illustrative courses 3Blue1Brown (see our previous reviews on linear algebra and math analysis) with a course on neural networks.

The first video is devoted to the structure of the components of the neural network, the second - to its training, the third - to the algorithm of this process. As a task for training, the classical task of recognizing numbers written by hand was taken.

A multilayer perceptron is considered in detail - a basic (but already quite complex) model for understanding any more modern versions of neural networks.

The purpose of the first video is to show what a neural network is. Using the example of the problem of digit recognition, the structure of the components of the neural network is visualized. The video has Russian subtitles.

Number Recognition Problem Statement

Let's say you have the number 3 drawn at an extremely low resolution of 28x28 pixels. Your brain can easily recognize this number.

From a computational standpoint, it's amazing how easy the brain is to perform this operation, even though the exact arrangement of the pixels varies greatly from one image to the next.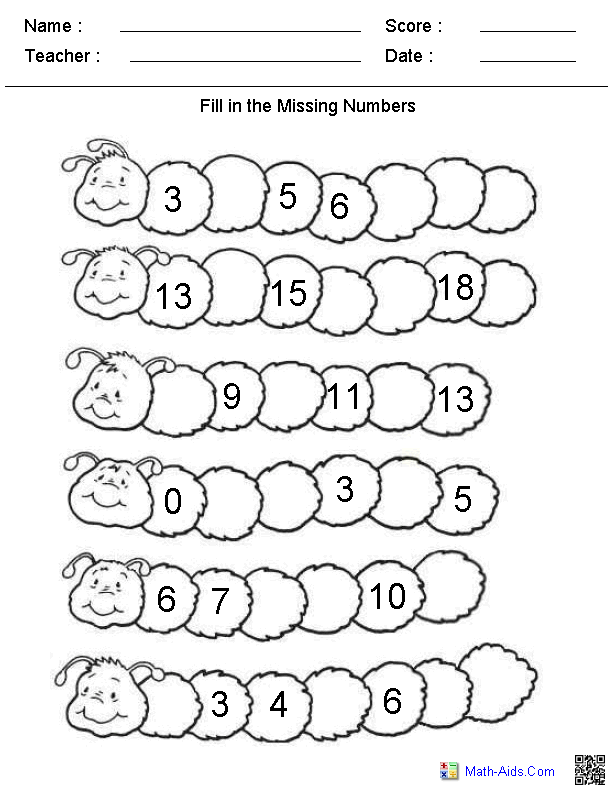 Something in our visual cortex decides that all threes, no matter how they are depicted, represent the same entity. Therefore, the task of recognizing numbers in this context is perceived as simple.

But if you were asked to write a program that takes as input an image of any number in the form of an array of 28x28 pixels and outputs the “entity” itself - a number from 0 to 9, then this task would cease to seem simple.

As the name suggests, the device of the neural network is somewhat close to the device of the neural network of the brain. For now, for simplicity, we will imagine that in the mathematical sense, in neural networks, neurons are understood as a certain container containing a number from zero to one.

Neuron activation. Neural network layers

Since our grid consists of 28x28=784 pixels, let there be 784 neurons containing different numbers from 0 to 1: the closer the pixel is to white, the closer the corresponding number is to one. These numbers filling the grid will be called activations of neurons. You can imagine this as if a neuron lights up like a light bulb when it contains a number close to 1 and goes out when a number is close to 0.

The described 784 neurons form the first layer of the neural network. The last layer contains 10 neurons, each corresponding to one of the ten digits. In these numbers, activation is also a number from zero to one, reflecting how confident the system is that the input image contains the corresponding digit.

There are also a couple of middle layers, called hidden layers, which we'll get to shortly. The choice of the number of hidden layers and the neurons they contain is arbitrary (we chose 2 layers of 16 neurons each), but usually they are chosen from certain ideas about the task being solved by the neural network.

The principle of the neural network is that the activation in one layer determines the activation in the next. Being excited, a certain group of neurons causes the excitation of another group.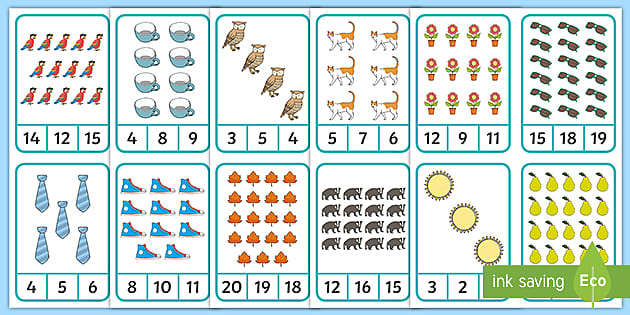 If we pass the trained neural network to the first layer the activation values ​​according to the brightness of each pixel of the image, the chain of activations from one layer of the neural network to the next will lead to the preferential activation of one of the neurons of the last layer corresponding to the recognized digit - the choice of the neural network.

Purpose of hidden layers

Before delving into the mathematics of how one layer affects the next, how learning occurs, and how the neural network solves the problem of recognizing numbers, we will discuss why such a layered structure can act intelligently at all. What do intermediate layers do between input and output layers?

Figure Image Layer

In the process of digit recognition, we bring the various components together. For example, a nine consists of a circle on top and a line on the right. The figure eight also has a circle at the top, but instead of a line on the right, it has a paired circle at the bottom. The four can be represented as three lines connected in a certain way. And so on.

In the idealized case, one would expect each neuron from the second layer to correspond to one of these components. And, for example, when you feed an image with a circle at the top to the neural network, there is a certain neuron whose activation will become closer to one. Thus, the transition from the second hidden layer to the output corresponds to the knowledge of which set of components corresponds to which digit.

Layer of images of structural units

The circle recognition task can also be divided into subtasks. For example, to recognize various small faces from which it is formed. Likewise, a long vertical line can be thought of as a pattern connecting several smaller pieces. Thus, it can be hoped that each neuron from the first hidden layer of the neural network performs the operation of recognizing these small edges.

Thus entered image leads to the activation of certain neurons of the first hidden layer, which determine the characteristic small pieces, these neurons in turn activate larger shapes, as a result, activating the neuron of the output layer associated with a certain number.

Whether or not the neural network will act this way is another matter that you will return to when discussing the network learning process. However, this can serve as a guide for us, a kind of goal of such a layered structure.

On the other hand, such a definition of edges and patterns is useful not only in the problem of digit recognition, but also in the problem of pattern detection in general.

And not only for recognition of numbers and images, but also for other intellectual tasks that can be divided into layers of abstraction. For example, for speech recognition, individual sounds, syllables, words, then phrases, more abstract thoughts, etc. are extracted from raw audio.

Determining the recognition area

To be specific, let's now imagine that the goal of a single neuron in the first hidden layer is to determine whether the picture contains a face in the area marked in the figure.

The first question is: what settings should the neural network have in order to be able to detect this pattern or any other pixel pattern.

Let's assign a numerical weight w _i to each connection between our neuron and the neuron from the input layer. Then we take all the activations from the first layer and calculate their weighted sum according to these weights.

Since the number of weights is the same as the number of activations, they can also be mapped to a similar grid. We will denote positive weights with green pixels, and negative weights with red pixels. The brightness of the pixel will correspond to the absolute value of the weight.

Now, if we set all weights to zero, except for the pixels that match our template, then the weighted sum is the sum of the activation values ​​of the pixels in the region of interest.

If you want to determine if there is an edge, you can add red weight faces around the green weight rectangle, corresponding to negative weights. Then the weighted sum for this area will be maximum when the average pixels of the image in this area are brighter, and the surrounding pixels are darker.

Activation scaling to interval [0, 1]

By calculating such a weighted sum, you can get any number in a wide range of values. In order for it to fall within the required range of activations from 0 to 1, it is reasonable to use a function that would “compress” the entire range to the interval [0, 1].

The sigmoid logistic function is often used for this scaling. The greater the absolute value of the negative input number, the closer the sigmoid output value is to zero. The larger the value of the positive input number, the closer the value of the function is to one.

Thus, neuron activation is essentially a measure of how positive the corresponding weighted sum is. To prevent the neuron from firing at small positive numbers, you can add a negative number to the weighted sum - a bias, which determines how large the weighted sum should be in order to activate the neuron.

So far we've only talked about one neuron. Each neuron from the first hidden layer is connected to all 784 pixel neurons of the first layer. And each of these 784 compounds will have a weight associated with it. Also, each of the neurons in the first hidden layer has a shift associated with it, which is added to the weighted sum before this value is "compressed" by the sigmoid. Thus, for the first hidden layer, there are 784x16 weights and 16 shifts.

Connections between other layers also contain the weights and offsets associated with them. Thus, for the given example, about 13 thousand weights and shifts that determine the behavior of the neural network act as adjustable parameters.

To train a neural network to recognize numbers means to force the computer to find the correct values ​​for all these numbers in such a way that it solves the problem. Imagine adjusting all those weights and manually shifting. This is one of the most effective arguments to interpret the neural network as a black box - it is almost impossible to mentally track the joint behavior of all parameters.

Description of a neural network in terms of linear algebra

Let's discuss a compact way of mathematical representation of neural network connections. Combine all activations of the first layer into a column vector. We combine all the weights into a matrix, each row of which describes the connections between the neurons of one layer with a specific neuron of the next (in case of difficulty, see the linear algebra course we described). As a result of multiplying the matrix by the vector, we obtain a vector corresponding to the weighted sums of activations of the first layer. We add the matrix product with the shift vector and wrap the sigmoid function to scale the ranges of values. As a result, we get a column of corresponding activations.

Obviously, instead of columns and matrices, as is customary in linear algebra, one can use their short notation. This makes the corresponding code both simpler and faster, since the machine learning libraries are optimized for vector computing.

Neuronal activation clarification

It's time to refine the simplification we started with. Neurons correspond not just to numbers - activations, but to activation functions that take values ​​from all neurons of the previous layer and calculate output values ​​in the range from 0 to 1.

In fact, the entire neural network is one large learning-adjustable function with 13,000 parameters that takes 784 input values ​​and gives the probability that the image corresponds to one of the ten digits intended for recognition. However, despite its complexity, this is just a function, and in a sense it is logical that it looks complicated, because if it were simpler, this function would not be able to solve the problem of recognizing digits.

As a supplement, let's discuss which activation functions are currently used to program neural networks.

Addition: a little about the activation functions. Comparison of the sigmoid and ReLU

Let's briefly touch on the topic of functions used to "compress" the interval of activation values. The sigmoid function is an example that emulates biological neurons and was used in early work on neural networks, but the simpler ReLU function is now more commonly used to facilitate neural network training.

The ReLU function corresponds to the biological analogy that neurons may or may not be active. If a certain threshold is passed, then the function is triggered, and if it is not passed, then the neuron simply remains inactive, with an activation equal to zero.

It turned out that for deep multilayer networks, the ReLU function works very well and it often makes no sense to use the more difficult sigmoid function to calculate.

The question arises: how does the network described in the first lesson find the appropriate weights and shifts only from the received data? This is what the second lesson is about.

In general, the algorithm is to show the neural network a set of training data representing pairs of images of handwritten numbers and their abstract mathematical representations.

In general terms

As a result of training, the neural network should correctly distinguish numbers from previously unrepresented test data. Accordingly, the ratio of the number of acts of correct recognition of digits to the number of elements of the test sample can be used as a test for training the neural network.

Where does training data come from? The problem under consideration is very common, and to solve it, a large MNIST database was created, consisting of 60 thousand labeled data and 10 thousand test images.

Cost function

Conceptually, the task of training a neural network is reduced to finding the minimum of a certain function - the cost function. Let's describe what it is.

As you remember, each neuron of the next layer is connected to the neuron of the previous layer, while the weights of these connections and the total shift determine its activation function. In order to start somewhere, we can initialize all these weights and shifts with random numbers.

Accordingly, at the initial moment, an untrained neural network in response to an image of a given number, for example, an image of a triple, the output layer gives a completely random answer.

To train the neural network, we will introduce a cost function, which will, as it were, tell the computer in the event of a similar result: “No, bad computer! The activation value must be zero for all neurons except for the one that is correct.”

Set cost function for digit recognition

Mathematically, this function represents the sum of the squared differences between the actual activation values ​​of the output layer and their ideal values. For example, in the case of a triple, the activation must be zero for all neurons, except for the one corresponding to the triple, for which it is equal to one.

It turns out that for one image we can determine one current value of the cost function. If the neural network is trained, this value will be small, ideally tending to zero, and vice versa: the larger the value of the cost function, the worse the neural network is trained.

Thus, in order to subsequently determine how well the neural network was trained, it is necessary to determine the average value of the cost function for all images of the training set.

This is a rather difficult task. If our neural network has 784 pixels at the input, 10 values ​​at the output and requires 13 thousand parameters to calculate them, then the cost function is a function of these 13 thousand parameters, it produces one single cost value that we want to minimize, and at the same time in the entire training set serves as parameters.

How to change all these weights and shifts so that the neural network is trained?

Gradient Descent

To start, instead of representing a function with 13k inputs, let's start with a function of one variable, C(w). As you probably remember from the course of mathematical analysis, in order to find the minimum of a function, you need to take the derivative.

However, the form of a function can be very complex, and one flexible strategy is to start at some arbitrary point and step down the value of the function. By repeating this procedure at each subsequent point, one can gradually come to a local minimum of the function, as does a ball rolling down a hill.

As shown in the figure above, a function can have many local minima, and which local minimum the algorithm ends up in depends on the choice of starting point, and there is no guarantee that the minimum found is the minimum possible value of the cost function. This must be kept in mind. In addition, in order not to "slip" the value of the local minimum, you need to change the step size in proportion to the slope of the function.

Slightly complicating this problem, instead of a function of one variable, you can represent a function of two variables with one output value. The corresponding function for finding the direction of the fastest descent is the negative gradient -∇C. The gradient is calculated, a step is taken in the direction of -∇С, the procedure is repeated until we are at the minimum.

The described idea is called gradient descent and can be applied to find the minimum of not only a function of two variables, but also 13 thousand, and any other number of variables. Imagine that all weights and shifts form one large column vector w. For this vector, you can calculate the same cost function gradient vector and move in the appropriate direction by adding the resulting vector to the w vector. And so repeat this procedure until the function С(w) comes to a minimum.

Gradient Descent Components

For our neural network, steps towards a lower cost function value will mean less and less random behavior of the neural network in response to training data. The algorithm for efficiently calculating this gradient is called backpropagation and will be discussed in detail in the next section.

For gradient descent, it is important that the output values ​​of the cost function change smoothly. That is why activation values ​​are not just binary values ​​of 0 and 1, but represent real numbers and are in the interval between these values.

Each gradient component tells us two things. The sign of a component indicates the direction of change, and the absolute value indicates the effect of this component on the final result: some weights contribute more to the cost function than others.

Checking the assumption about the assignment of hidden layers

Let's discuss the question of how the layers of the neural network correspond to our expectations from the first lesson. If we visualize the weights of the neurons of the first hidden layer of the trained neural network, we will not see the expected figures that would correspond to the small constituent elements of the numbers. We will see much less clear patterns corresponding to how the neural network has minimized the cost function.

On the other hand, the question arises, what to expect if we pass an image of white noise to the neural network? It could be assumed that the neural network should not produce any specific number and the neurons of the output layer should not be activated or, if they are activated, then in a uniform way. Instead, the neural network will respond to a random image with a well-defined number.

Although the neural network performs digit recognition operations, it has no idea how they are written. In fact, such neural networks are a rather old technology developed in the 80s-90 years. However, it is very useful to understand how this type of neural network works before understanding modern options that can solve various interesting problems. But the more you dig into what the hidden layers of a neural network are doing, the less intelligent the neural network seems to be.

Learning on structured and random data

Consider an example of a modern neural network for recognizing various objects in the real world.

What happens if you shuffle the database so that the object names and images no longer match? Obviously, since the data is labeled randomly, the recognition accuracy on the test set will be useless. However, at the same time, on the training sample, you will receive recognition accuracy at the same level as if the data were labeled in the right way.

Millions of weights on this particular modern neural network will be fine-tuned to exactly match the data and its markers. Does the minimization of the cost function correspond to some image patterns, and does learning on randomly labeled data differ from training on incorrectly labeled data?

If you train a neural network for the recognition process on randomly labeled data, then training is very slow, the cost curve from the number of steps taken behaves almost linearly. If training takes place on structured data, the value of the cost function decreases in a much smaller number of iterations.

Backpropagation is a key neural network training algorithm. Let us first discuss in general terms what the method consists of.

Neuron activation control

Each step of the algorithm uses in theory all examples of the training set. Let us have an image of a 2 and we are at the very beginning of training: weights and shifts are set randomly, and some random pattern of output layer activations corresponds to the image.

We cannot directly change the activations of the final layer, but we can influence the weights and shifts to change the activation pattern of the output layer: decrease the activation values ​​of all neurons except the corresponding 2, and increase the activation value of the desired neuron. In this case, the increase and decrease is required the stronger, the farther the current value is from the desired one.

Neural network settings

Let's focus on one neuron, corresponding to the activation of neuron 2 on the output layer. As we remember, its value is the weighted sum of the activations of the neurons of the previous layer plus the shift, wrapped in a scaling function (sigmoid or ReLU).

So to increase the value of this activation, we can:

1. Increase the shift b.
2. Increase weights w _i .
3. Swap previous layer activations a _i .

From the weighted sum formula, it can be seen that the weights corresponding to connections with the most activated neurons make the greatest contribution to neuron activation. A strategy similar to biological neural networks is to increase the weights w _i in proportion to the activation value a _i of the corresponding neurons of the previous layer. It turns out that the most activated neurons are connected to the neuron that we only want to activate with the most "strong" connections.

Another close approach is to change the activations of neurons of the previous layer a _i in proportion to the weights w _i . We cannot change the activation of neurons, but we can change the corresponding weights and shifts and thus affect the activation of neurons.

Backpropagation

The penultimate layer of neurons can be considered similarly to the output layer. You collect information about how the activations of neurons in this layer would have to change in order for the activations of the output layer to change.

It is important to understand that all these actions occur not only with the neuron corresponding to the two, but also with all the neurons of the output layer, since each neuron of the current layer is connected to all the neurons of the previous one.

Having summed up all these necessary changes for the penultimate layer, you understand how the second layer from the end should change. Then, recursively, you repeat the same process to determine the weight and shift properties of all layers.

Classic Gradient Descent

As a result, the entire operation on one image leads to finding the necessary changes of 13 thousand weights and shifts. By repeating the operation on all examples of the training sample, you get the change values ​​for each example, which you can then average for each parameter separately.

The result of this averaging is the negative gradient column vector of the cost function.

Stochastic Gradient Descent

Considering the entire training set to calculate a single step slows down the gradient descent process. So the following is usually done.

The data of the training sample are randomly mixed and divided into subgroups, for example, 100 labeled images. Next, the algorithm calculates the gradient descent step for one subgroup.

This is not exactly a true gradient for the cost function, which requires all the training data, but since the data is randomly selected, it gives a good approximation, and, importantly, allows you to significantly increase the speed of calculations.

If you build the learning curve of such a modernized gradient descent, it will not look like a steady, purposeful descent from a hill, but like a winding trajectory of a drunk, but taking faster steps and also coming to a function minimum.

This approach is called stochastic gradient descent.

Supplement. Backpropagation Math

Now let's look a little more formally at the mathematical background of the backpropagation algorithm.

Primitive neural network model

Let's start with an extremely simple neural network consisting of four layers, where each layer has only one neuron.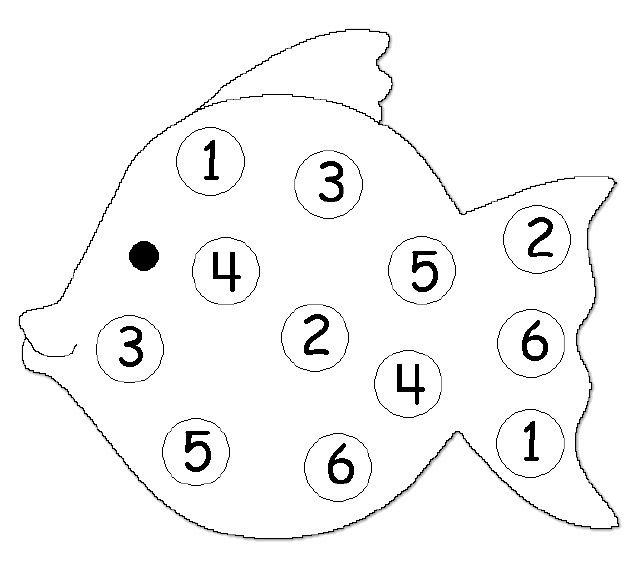 Accordingly, the network has three weights and three shifts. Consider how sensitive the function is to these variables.

Let's start with the connection between the last two neurons. Let's denote the last layer L, the penultimate layer L-1, and the activations of the considered neurons lying in them a ^(L) , a ^(L-1) .

Cost function

Imagine that the desired activation value of the last neuron given to the training examples is y, equal to, for example, 0 or 1. Thus, the cost function is defined for this example as

C ₀ = (a ^{( L)} - y) ² .

Recall that the activation of this last neuron is given by the weighted sum, or rather the scaling function of the weighted sum: ^(L) ).

For brevity, the weighted sum can be denoted by a letter with the appropriate index, for example z ^(L) :

a ^(L) = σ (z ^(L) ).

Consider how small changes in the weight w affect the value of the cost function ^(L) . Or in mathematical terms, what is the derivative of the cost function with respect to weight ∂C ₀ /∂w ^(L) ?

It can be seen that the change in C ₀ depends on the change in a ^(L) , which in turn depends on the change in z ^(L) , which depends on w ^(L) . According to the rule of taking similar derivatives, the desired value is determined by the product of the following partial derivatives:.

Definition of derivatives

Calculate the corresponding derivatives: and desired.

The average derivative in the chain is simply the derivative of the scaling function:

∂a ^(L) /∂z ^(L) = σ'(z ^(L) )

/∂w ^(L) = a ^(L-1)

Thus, the corresponding change is determined by how activated the previous neuron is. This is consistent with the idea mentioned above that a stronger connection is formed between neurons that light up together.

Final expression:

∂C ₀ /∂w ^(L) = 2(a ^(L) - y) σ'(z ^(L) ) a ^(L-1)

Backpropagation3

Recall that a certain derivative is only for the cost of a single example of a training sample C ₀ . For the cost function C, as we remember, it is necessary to average over all examples of the training sample: The resulting average value for a specific w ^(L) is one of the components of the cost function gradient. The consideration for shifts is identical to the above consideration for weights.

Having obtained the corresponding derivatives, we can continue the consideration for the previous layers.

Model with many neurons in the layer

However, how to make the transition from layers containing one neuron to the initially considered neural network. Everything will look the same, just an additional subscript will be added, reflecting the number of the neuron within the layer, and the weights will have double subscripts, for example, jk, reflecting the connection of neuron j from one layer L with another neuron k in layer L-1.

The final derivatives give the necessary components to determine the components of the ∇C gradient.

You can practice the described digit recognition task using the training repository on GitHub and the mentioned MNIST digit recognition dataset.

• Writing your own neural network: a step-by-step guide
• Neural Networks Toolkit
• Illustrative video course in linear algebra: 11 lessons
• Introduction to Deep Learning
• Illustrative video course of mathematical analysis: 10 lessons
• Beginner to Pro in Machine Learning in 3 Months

Building a program to recognize handwritten numbers with tensorflow and tkinter

Developers use machine learning and deep learning to make computers smarter. A person learns by performing a certain task, practicing and repeating it over and over again, remembering exactly how it is done. The neurons in the brain then fire automatically and can quickly complete the learned task.

Deep learning works in a similar way. It uses different types of neural network architecture depending on the types of problems. For example, object recognition, image and sound classification, object identification, image segmentation, and so on.

What is handwritten digit recognition?

Handwritten digit recognition is the ability of a computer to recognize handwritten digits. For a machine, this is not the easiest task, because each written number may differ from the reference spelling. In the case of recognition, the solution is that the machine is able to recognize the digit in the image.

About the Python project

In this tutorial, we'll implement a handwritten digit recognition application using the MNIST dataset. We use a special type of deep neural network called a convolutional neural network. And in the end, we will create a graphical interface in which it will be possible to draw a number and immediately recognize it.

Requirements

This project requires basic knowledge of Python programming, the Keras library for deep learning, and the Tkinter library for creating a GUI.

Install the required libraries for the project with pip install .

Libraries: numpy, tensorflow, keras, pillow.

MNIST Dataset

This is probably one of the most popular datasets among machine learning and deep learning enthusiasts. It contains 60,000 practice images of handwritten numbers from 0 to 9, as well as 10,000 pictures for testing. There are 10 different classes in the set. Images with numbers are presented as 28 x 28 matrices, where each cell contains a certain shade of gray.

Creating a Python project for handwritten digit recognition

Download project files

1.

First, you need to import all the modules that will be required to train the model. The Keras library already includes some of them. Among them is MNIST. This way you can easily import a set and start working with it. Method mnist.load_data() returns training data, their labels, and test data with labels.

 import keras from keras.datasets import mnist from keras.models import Sequential from keras.layers import Dense, Dropout, Flatten from keras.layers import Conv2D, MaxPooling2D from keras import backend as K # download the data and divide it into training nador and test nador (x_train, y_train), (x_test, y_test) = mnist.load_data() print(x_train.shape, y_train.shape) 

2. Data pre-processing

Data from the image cannot be directly transferred to the model, so first you need to perform certain operations by processing the data in order for the neural network to work with them. Training data dimension - (60000, 28, 28) . The convolutional neural network model requires one dimension, so the shape (60000, 28, 28, 1) will need to be rebuilt.

 num_classes = 10 x_train = x_train.reshape(x_train.shape[0], 28, 28, 1) x_test = x_test.reshape(x_test.shape[0], 28, 28, 1) input_shape = (28, 28, 1) # convert vector classes to binary matrices y_train = keras.utils.to_categorical(y_train, num_classes) y_test = keras.utils.to_categorical(y_test, num_classes) x_train = x_train.astype('float32') x_test = x_test.astype('float32') x_train /= 255 x_test /= 255 print('Dimension x_train:', x_train.shape) print(x_train.shape[0], 'Train size') print(x_test.shape[0], 'Size of test') 

3. Creating a model

The next step is to create a convolutional neural network model. It predominantly consists of convolutional and subsampling layers. The model works better with data represented as grid structures. That's why such a network is great for image classification problems. The exclusion layer is used to turn off individual neurons and during training. It reduces the chance of overfitting. Then the model is compiled using the optimizer Adadelta .

 batch_size = 128 epochs = 10 model = Sequential() model.add(Conv2D(32, kernel_size=(3, 3),activation='relu',input_shape=input_shape)) model.add(Conv2D(64, (3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(256, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(num_classes, activation='softmax')) model.compile(loss=keras.losses.categorical_crossentropy,optimizer=keras.optimizers.Adadelta(),metrics=['accuracy']) 

4. Model training

Keras function model.fit() will start model training. It accepts training, validation data, epochs ( epoch ) and batch size ( batch ).

Model training takes some time. After that, the weights and model definition are saved in the file mnist.h5 .

 hist = model. fit(x_train, y_train, batch_size = batch_size, epochs=epochs, verbose=1, validation_data=(x_test, y_test)) print("Model trained successfully") model.save('mnist.h5') print("Model saved as mnist.h5") 

5. Evaluate the model

There are 10,000 images in the dataset that are used to evaluate the performance of the model. The test data is not used during training and is therefore new to the model. The MNIST set is well balanced, so you can expect around 99% accuracy.

 score = model.evaluate(x_test, y_test, verbose=0) print('Test loss:', score[0]) print('Test Accuracy:', score[1]) 

6. Creating a graphical interface for predicting numbers

Let's create a new file for the graphical interface, which will contain an interactive window for drawing numbers on the canvas and a button responsible for the recognition process. The Tkinter library is part of the Python standard library. The function predict_digit() takes an input image and then uses the trained network to predict.

Then we create the class App , which will be responsible for building the application's graphical interface. Create a canvas that you can draw on by capturing mouse events. The button will activate function predict_digit() and display the result.

Further all the code from the file gui_digit_recognizer.py :

 from keras.models import load_model from tkinter import * import tkinter as tk import win32gui from PIL import ImageGrab, Image import numpy as np model = load_model('mnist.h5') def predict_digit(img): # resize images to 28x28 img = img.resize((28,28)) # convert rgb to grayscale img = img.convert('L') img = np.array(img) # resizing to support model input and normalization img = img.reshape(1,28,28,1) img=img/255.0 # predict number res = model.predict([img])[0] return np.argmax(res), max(res) classApp(tk.Tk): def __init__(self): tk.Tk.__init__(self) self. x = self.y = 0 # Create elements self.canvas = tk.Canvas(self, width=300, height=300, bg = "white", cursor="cross") self.label = tk.Label(self, text="Think..", font=("Helvetica", 48)) self.classify_btn = tk.Button(self, text = "Recognize", command = self.classify_handwriting) self.button_clear = tk.Button(self, text = "Clear", command = self.clear_all) # Window Grid self.canvas.grid(row=0, column=0, pady=2, sticky=W, ) self.label.grid(row=0, column=1,pady=2, padx=2) self.classify_btn.grid(row=1, column=1, pady=2, padx=2) self.button_clear.grid(row=1, column=0, pady=2) # self.canvas.bind("", self.start_pos) self.canvas.bind("", self.draw_lines) def clear_all(self): self.canvas.delete("all") def classify_handwriting(self): HWND = self.canvas.winfo_id() rect = win32gui.GetWindowRect(HWND) # get canvas coordinate im = ImageGrab. 
Learn more

		
The goldilocks story
				
Shape definition for kids
				
Reading lexile test
				
Matching letters to sounds
				
How to help a 5 year old read
				
The story of alphabet
				
What is red riding hood about
				
Best word help
				
Pterodactyl what do they eat
				
Preschool learning letters games
				
How to teach reading skill