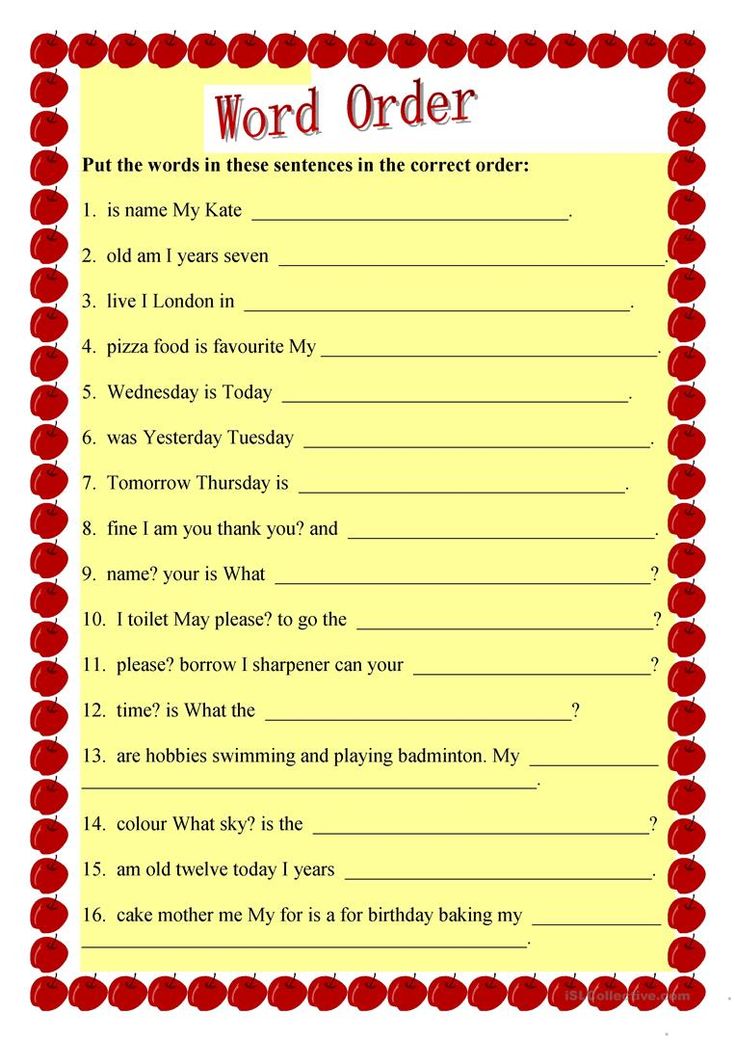
Definition of alphabetic principle
The Alphabetic Principle | Reading Rockets
Not knowing letter names is related to children's difficulty in learning letter sounds and in recognizing words. Children cannot understand and apply the alphabetic principle (understanding that there are systematic and predictable relationships between written letters and spoken sounds) until they can recognize and name a number of letters.
Children whose alphabetic knowledge is not well developed when they start school need sensibly organized instruction that will help them identify, name, and write letters. Once children are able to identify and name letters with ease, they can begin to learn letter sounds and spellings.
Children appear to acquire alphabetic knowledge in a sequence that begins with letter names, then letter shapes, and finally letter sounds. Children learn letter names by singing songs such as the "Alphabet Song," and by reciting rhymes. They learn letter shapes as they play with blocks, plastic letters, and alphabetic books.
Informal but planned instruction in which children have many opportunities to see, play with, and compare letters leads to efficient letter learning. This instruction should include activities in which children learn to identify, name, and write both upper case and lower case versions of each letter.
What is the "alphabetic principle"?
Children's reading development is dependent on their understanding of the alphabetic principle – the idea that letters and letter patterns represent the sounds of spoken language. Learning that there are predictable relationships between sounds and letters allows children to apply these relationships to both familiar and unfamiliar words, and to begin to read with fluency.
The goal of phonics instruction is to help children to learn and be able to use the Alphabetic Principle. The alphabetic principle is the understanding that there are systematic and predictable relationships between written letters and spoken sounds. Phonics instruction helps children learn the relationships between the letters of written language and the sounds of spoken language.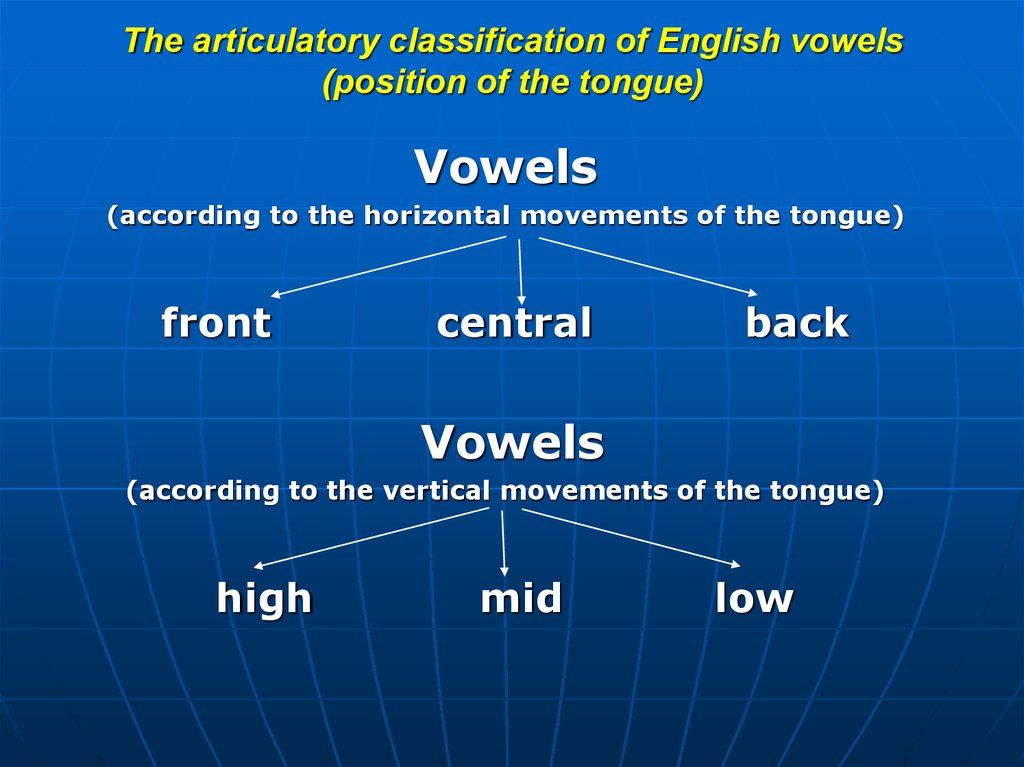
Two issues of importance in instruction in the alphabetic principle are the plan of instruction and the rate of instruction.
The alphabetic principle plan of instruction
- Teach letter-sound relationships explicitly and in isolation.
- Provide opportunities for children to practice letter-sound relationships in daily lessons.
- Provide practice opportunities that include new sound-letter relationships, as well as cumulatively reviewing previously taught relationships.
- Give children opportunities early and often to apply their expanding knowledge of sound-letter relationships to the reading of phonetically spelled words that are familiar in meaning.
Rate and sequence of instruction
No set rule governs how fast or how slow to introduce letter-sound relationships. One obvious and important factor to consider in determining the rate of introduction is the performance of the group of students with whom the instruction is to be used.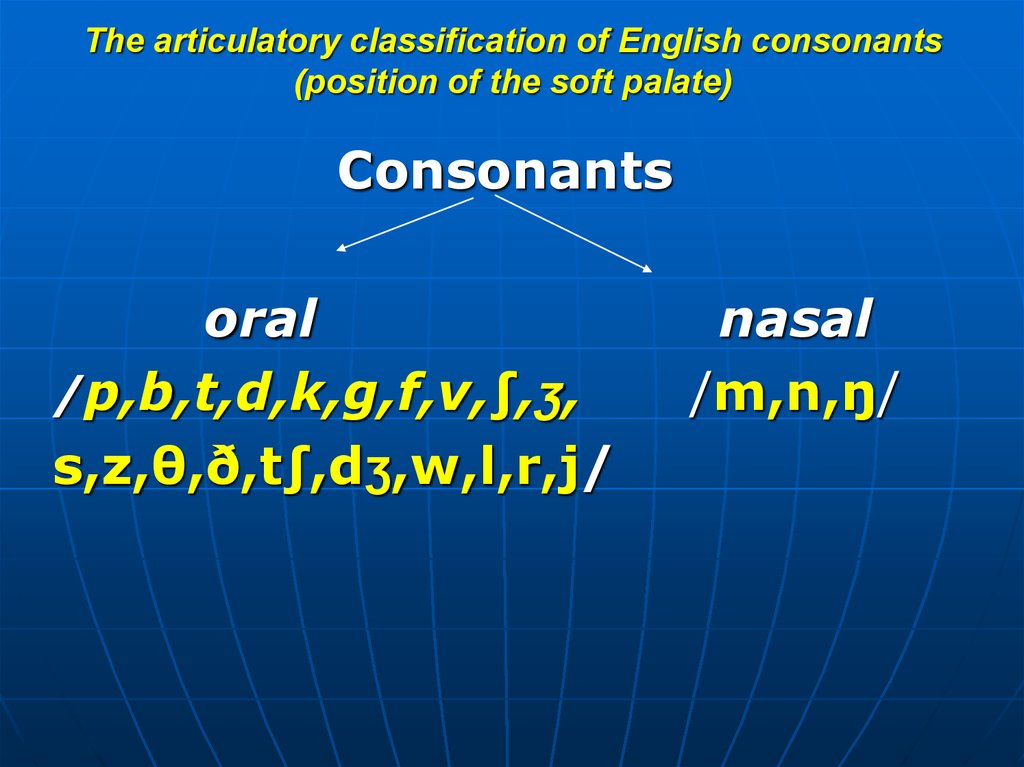
Furthermore, there is no agreed upon order in which to introduce the letter-sound relationships. It is generally agreed, however, that the earliest relationships introduced should be those that enable children to begin reading words as soon as possible. That is, the relationships chosen should have high utility. For example, the spellings m, a, t, s, p, and h are high utility, but the spellings x as in box, gh, as in through, ey as in they, and a as in want are of lower utility.
It is also a good idea to begin instruction in sound-letter relationships by choosing consonants such as f, m, n, r, and s, whose sounds can be pronounced in isolation with the least distortion. Stop sounds at the beginning or middle of words are harder for children to blend than are continuous sounds.
Instruction should also separate the introduction of sounds for letters that are auditorily confusing, such as /b/ and /v/ or /i/ and /e/, or visually confusing, such as b and d or p and g.
Instruction might start by introducing two or more single consonants and one or two short vowel sounds. It can then add more single consonants and more short vowel sounds, with perhaps one long vowel sound. It might next add consonant blends, followed by digraphs (for example, th, sh, ch), which permits children to read common words such as this, she, and chair. Introducing single consonants and consonant blends or clusters should be introduced in separate lessons to avoid confusion.
The point is that the order of introduction should be logical and consistent with the rate at which children can learn. Furthermore, the sound-letter relationships chosen for early introduction should permit children to work with words as soon as possible.
Many teachers use a combination of instructional methods rather than just one. Research suggests that explicit, teacher-directed instruction is more effective in teaching the alphabetic principle than is less-explicit and less-direct instruction.
Guidelines for rate and sequence of instruction
- Recognize that children learn sound-letter relationships at different rates.
- Introduce sound-letter relationships at a reasonable pace, in a range from two to four letter-sound relationships a week.
- Teach high-utility letter-sound relationships early.
- Introduce consonants and vowels in a sequence that permits the children to read words quickly.
- Avoid the simultaneous introduction of auditorily or visually similar sounds and letters.
- Introduce single consonant sounds and consonant blends/clusters in separate lessons.
- Provide blending instruction with words that contain the letter-sound relationships that children have learned.
Alphabetic Principle | Reading Rockets
Children's knowledge of letter names and shapes is a strong predictor of their success in learning to read. Knowing letter names is strongly related to children's ability to remember the forms of written words and their ability to treat words as sequences of letters.
Children whose alphabetic knowledge is not well developed when they start school need sensibly organized instruction that will help them identify, name, and write letters. Once children are able to identify and name letters with ease, they can begin to learn letter sounds and spellings.
Children appear to acquire alphabetic knowledge in a sequence that begins with letter names, then letter shapes, and finally letter sounds. Children learn letter names by singing songs such as the "Alphabet Song," and by reciting rhymes. They learn letter shapes as they play with blocks, plastic letters, and alphabetic books. Informal but planned instruction in which children have many opportunities to see, play with, and compare letters leads to efficient letter learning. This instruction should include activities in which children learn to identify, name, and write both upper case and lower case versions of each letter.
What is the "alphabetic principle"?
Children's reading development is dependent on their understanding of the alphabetic principle — the idea that letters and letter patterns represent the sounds of spoken language.
Learning that there are predictable relationships between sounds and letters allows children to apply these relationships to both familiar and unfamiliar words, and to begin to read with fluency.
The goal of phonics instruction is to help children to learn and be able to use the Alphabetic Principle. The alphabetic principle is the understanding that there are systematic and predictable relationships between written letters and spoken sounds. Phonics instruction helps children learn the relationships between the letters of written language and the sounds of spoken language.
The alphabetic principle plan of instruction
The literacy program:
- Teaches letter-sound relationships explicitly and in isolation.
- Provides opportunities for children to practice letter-sound relationships in daily lessons.
- Provides practice opportunities that include new sound-letter relationships, as well as cumulatively reviewing previously taught relationships.
- Gives children opportunities early and often to apply their expanding knowledge of sound-letter relationships to the reading of phonetically spelled words that are familiar in meaning.
Rate and sequence of introduction
No set rule governs how fast or how slow to introduce letter-sound relationships. One obvious and important factor to consider in determining the rate of introduction is the performance of the group of students with whom the instruction is to be used. Furthermore, there is no agreed upon order in which to introduce the letter-sound relationships. It is generally agreed, however, that the earliest relationships introduced should be those that enable children to begin reading words as soon as possible. That is, the relationships chosen should have high utility. For example, the spellings m, a, t, s, p, and h are high utility, but the spellings x as in box, gh, as in through, ey as in they, and a as in want are of lower utility.
It is also a good idea to begin instruction in sound-letter relationships by choosing consonants such as f, m, n, r, and s, whose sounds can be pronounced in isolation with the least distortion.
Stop sounds at the beginning or middle of words are harder for children to blend than are continuous sounds.
Instruction should also separate the introduction of sounds for letters that are auditorally confusing, such as /b/ and /v/ or /i/ and /e/, or visually confusing, such as b and d or p and g. Instruction might start by introducing two or more single consonants and one or two short vowel sounds. It can then add more single consonants and more short vowel sounds, with perhaps one long vowel sound. It might next add consonant blends, followed by digraphs (for example, th, sh, ch), which permits children to read common words such as this, she, and chair. Introducing single consonants and consonant blends or clusters should be introduced in separate lessons to avoid confusion.
The point is that the order of introduction should be logical and consistent with the rate at which children can learn.
Furthermore, the sound-letter relationships chosen for early introduction should permit children to work with words as soon as possible. Many teachers use a combination of instructional methods rather than just one. Research suggests that explicit, teacher-directed instruction is more effective in teaching the alphabetic principle than is less-explicit and less-direct instruction.
Guidelines for rate and sequence of introduction
The literacy program:
- Recognizes that children learn sound-letter relationships at different rates.
- Introduces sound-letter relationships at a reasonable pace, in a range from two to four letter-sound relationships a week.
- Teaches high-utility letter-sound relationships early.
- Introduces consonants and vowels in a sequence that permits the children to read words quickly.
- Avoids the simultaneous introduction of auditorially or visually similar sounds and letters.
- Introduces single consonant sounds and consonant blends/clusters in separate lessons.
- Provides blending instruction with words that contain the letter-sound relation.
Video: The Alphabetic Principle
In Houston, the teacher of an advanced kindergarten class connects letters and sounds in a systematic and explicit way.
90,000 alphabetical catalog: definitions, structure, principles ofSelect the subject
Technical
Aviation and missile and space equipment
Automation of technological processes
Automation and management
Architecture and construction
Database
Military business
Higher higher Mathematics
Geometry
Hydraulics
Machine parts
Rail transport
Engineering networks and equipment
Informatics
Information security
Information technology
Material science
Engineering
Metallurgy
Mechanics
Microprocessor Technician 9000 Programming
Processes and apparatuses
Welding and welding production
Material Resistance
Textile industry
Theoretical mechanics
Probability Theory
Games Theory
Theory of machines and mechanisms
Heat power industry
Technological machines and equipment
Food and goods
Vehicles 9000 9000 9000 Physics
Drafting
Electronics, electrical engineering, radio engineering
Energy Engineering
Nuclear Physics and Technologies
other
Natural
Agricultural chemistry and agricultural institution
Astronomy
Biology
Veterina Natural science
Land management and cadastre
Medicine
Oil and gas business
Horticulture
Pharmacy
Chemistry
Surgery
Ecology
Humanitarian
Acting
English
Library and Information Activities
Documentation and Archival Construction 9000
Chinese language
Conflictology
Local history
Criminology
Culinary
Culturology
Literature
Logic
International Relations
Music
German language
hairdresser
PEOPLE
Political science
Psychology
OFFICE
OFFICE IN Religion
Russian language
Public relations
Social work
Sociology
Physical culture
Philosophy
French
Ethics
Languages (translations)
Linguistics and philology
Economic Analysis
Anti-crisis Banking
Business Planning
Accounting and audit
Foreign economic activity
Hotel business
State and municipal administration
Money
Investments
Innovation Management
Credit
Logistics
Marketing
Management
Micro-
Micro-, Macroeconomics
Organizational Development
Production Marketing and Management 9000
Standardization
Statistics
Strategic management
Insurance
Customs
Management Theory
Military District
Trading
Tourism
Management
Management
Project management
9000Business economics
Labor economics
Economic theory
Economic analysis
EVIEWS
SPSS
STATA
Define the power of the alphabet.
Alphabetical approach to the measurement of information And many other concepts have the most direct connections with each other. Very few users today are sufficiently well versed in these matters. Let's try to clarify what the power of the alphabet is, how to calculate it and apply it in practice. In the future, this, no doubt, can be useful in practice.
How information is measured
Before starting to study the question of what is the power of the alphabet, and in general, what it is, we should start, so to speak, with the basics.
Surely everyone knows that today there are special systems for measuring any quantities based on reference values. For example, for distances and similar quantities, these are meters, for mass and weight - kilograms, for time intervals - seconds, etc.
But how can information be measured in terms of text size? It was for this that the concept of the cardinality of an alphabet was introduced.
What is the power of the alphabet: the initial concept
So, if we follow the generally accepted rule that the final value of any quantity is a parameter that determines how many times the reference unit is folded into the measured value, we can conclude: the power of the alphabet is the total number characters used for a particular language.
To make it clearer, let's leave aside the question of how to find the power of the alphabet, and pay attention to the symbols themselves, of course, from the point of view of information technology. Roughly speaking, the complete list of used characters contains letters, numbers, all kinds of brackets, special characters, punctuation marks, etc. However, if we approach the question of what is the power of the alphabet in a computer way, this should also include a space (a single gap between words or other characters).
Let's take the Russian language as an example, or rather, the keyboard layout. Based on the foregoing, the complete list contains 33 letters, 10 numbers and 11 special characters. Thus, the total power of the alphabet is equal to 54.
Information weight of characters
However, the general concept of the power of the alphabet does not define the essence of calculating the information volumes of text containing letters, numbers and symbols.
This requires a special approach.
In principle, think about it, well, what can be the minimum set from the point of view of a computer system, how many characters can it contain? Answer: two. And that's why. The fact is that each character, be it a letter or a number, has its own informational weight, by which the machine recognizes what is in front of it. But the computer understands only the representation in the form of ones and zeros, on which, in fact, all computer science is based.
Thus, any character can be represented as sequences containing the numbers 1 and 0, that is, the minimum sequence denoting a letter, number or symbol consists of two components.
The information weight itself, taken as a standard information unit of measurement, is called a bit (1 bit). Accordingly, 8 bits make up 1 byte.
Representation of characters in binary code
So, what is the power of the alphabet, I think, is already a little clear. Now let's look at another aspect, in particular, the practical representation of power using For simplicity, let's take an alphabet containing only 4 characters as an example.
In two-digit binary code, the sequence and their information representation can be described as follows:
| Sequence number | ||||
| Binary |
From here - the simplest conclusion: with the power of the alphabet N=4, the weight of a single character is 2 bits.
If using a three-digit binary code for the alphabet, for example, with 8 characters, the number of combinations will be:
| Ordinal number | ||||||||
| Binary |
In other words, if the power of the alphabet is N=8, the weight of one character for a three-digit binary code will be equal to 3 bits.
of the alphabet and use it in the computer expression
Now let's try to look at the relationship that expresses the number of characters in the code and the power of the alphabet. The formula, where N is the alphabetical power of the alphabet, and b is the number of characters in the binary code, will look like this:
That is, 2 1 \u003d 2, 2 2 \u003d 4, 2 3 \u003d 8, 2 4 \u003d 16, etc. . Roughly speaking, the desired number of characters of the binary code itself is the weight of the character. In terms of information, it looks like this:
Measuring the information volume
However, these were just the simplest examples, so to speak, for an initial understanding of what the power of the alphabet is. Let's go directly to practice.
At this stage of the development of computer technology for typing, taking into account capital, lowercase and Cyrillic and Latin letters, punctuation marks, brackets, arithmetic symbols, etc. 256 characters are used.
Based on the fact that 256 is 2 8 , it is easy to guess that the weight of each character in such an alphabet is 8, that is, 8 bits or 1 byte.
Based on all known parameters, we can easily get the value of the information volume of any text we need. For example, we have a computer text containing 30 pages. One page contains 50 lines of 60 any characters or symbols, including spaces.
Thus, one page will contain 50 x 60 = 3000 bytes of information, and the entire text - 3000 x 50 = 150000 bytes. As you can see, even small texts are inconvenient to measure in bytes. What about entire libraries?
In this case, it is better to convert the volume into more powerful values - kilobytes, megabytes, gigabytes, etc. Based on the fact that, for example, 1 kilobyte is equal to 1024 bytes (2 10), and a megabyte is 2 10 kilobytes (1024 kilobytes), it is easy to calculate that the amount of text in the information-mathematical expression for our example will be 150000/1024=146, 484375 kilobytes or approximately 0.
14305 megabytes.
Instead of an afterword
In general, this is all in a nutshell and everything that concerns the consideration of the question, what is the power of the alphabet. It remains to be added that a purely mathematical approach has been used in this description. It goes without saying that the semantic load of the text in this case is not taken into account.
But, if we approach the issues of consideration from a position that gives a person something to comprehend, a set of meaningless combinations or sequences of characters in this regard will have zero information load, although, from the point of view of the concept of information volume, the result is still possible calculate.
In general, knowledge about the power of the alphabet and related concepts is not so difficult to understand and can simply be applied in the sense of practical actions. At the same time, any user almost every day faces this. It is enough to cite as an example the popular editor Word or any other of the same level that uses such a system.
But do not confuse it with the usual Notepad. Here, the power of the alphabet is lower, since, say, uppercase letters are not used when typing.
We will denote this value by the letter N. For example, the power of the alphabet of Russian letters and marked additional characters is 54.
Imagine that the text comes to you sequentially, one character at a time, like a paper ribbon crawling out of a telegraph machine. Assume that each character appearing on the tape has the same probability of being any character in the alphabet. In reality, this is not entirely true, but for simplicity we will accept such an assumption. Any of N characters can appear in each successive position of the text. Then, according to the formula N = 2 I known to us (see the meaningful approach), each such symbol carries I bit of information, which can be determined from the solution of the equation: 2 I = 54. We get: I = 5.755 bits - this amount of information carries one symbol in Russian text.
To find the amount of information in the entire text, you need to count the number of characters in it and multiply by I.
Let's calculate the amount of information on one page of the book. Let the page contain 50 lines. Each line has 60 characters. This means that 50x60=3000 characters fit on the page. Then the amount of information will be equal to: 5.755 x 3000 = 17265 bits.
With an alphabetical approach to measuring information, the amount of information does not depend on the content, but on the size of the text and the power of the alphabet.
Thus, the alphabetical approach to measuring information can be represented as a diagram:
When using the binary system (the alphabet consists of two characters: 0 and 1), each binary character carries 1 bit of information.
The alphabetical approach is an objective way of measuring information as opposed to a subjective content approach.
It is most convenient to measure information when the size of the alphabet N is an integer power of two. For example, if N=16, then each character carries 4 bits of information because 2 4 = 16.
And if N = 32, then one character "weighs" 5 bits.
There is theoretically no limit to the maximum size of the alphabet. However, there is an alphabet that can be called sufficient. This is an alphabet with a capacity of 256 characters. In an alphabet of this size, you can put all practically necessary characters: Latin and Russian letters, numbers, signs of arithmetic operations, all kinds of brackets, punctuation marks ....
Since 256 = 2 8, then one character of this alphabet "weighs" 8 bits. Moreover, 8 bits of information is such a characteristic value that it was even given its own name - a byte.
1 byte = 8 bits.
The following units are used to measure large amounts of information:
1 Kb (one kilobyte) = 1024 bytes = 2 10 bytes
1 Mb (one megabyte) = 1024 Kb = 2 10 Kb = 2 20 bytes one gigabyte)= 1024 MB=2 10 MB=2 30 bytes
1TB (one terabyte)= 1024GB=2 10 GB=2 40 bytes
1PB(one petabyte)= 1024TB=2 10TB=2 50 bytes
1 Ebyte (one exabyte) = 1024 PB = 2 10 PB = 2 60 bytes
13byte(one zettabyte)= 1024Ebyte = 2 10Ebyte=2 70 bytes
Text encoding
Text information in a computer, like all other types of information, is encoded in binary codes.
Each character of the alphabet is assigned an integer, which is considered to be the code of this character.
Traditional encodings use a sequence of 8 zeros and ones to encode one character 8 bits = 1 byte .
There are 256 different sequences of 8 zeros and ones (2 8 = 256). Therefore, such an 8-bit code allows you to encode 256 different characters.
Assigning a specific numeric code to a character is a matter of convention. ASCII table adopted as international standard (American Standard Code for Information Interchange - American Standard Code for Information Interchange), encoding the first half of the characters with numeric codes from 0 to 127 (codes from 0 to 32 are assigned not to characters, but to function keys).
ASCII code table
To encode the characters of national alphabets, the ASCII code table extension is used, that is, 8-bit codes from 128 to 255.
contain codes of national alphabets, pseudographic symbols and some mathematical symbols.
Currently, there are 5 different Cyrillic encodings (KOI8, Windows. MSDOS, Macintosh, ISO), which causes certain difficulties when working with Russian-language documents.
At the end of the 90s, a new international Unicode standard appeared, which allocates not one byte, but two, for 1 character, so it can be used to encode 65536 different characters. It includes all existing, extinct and artificially created alphabets of the world, as well as many mathematical, musical, chemical and other symbols.
Measuring information.
Alphabetical approach to measuring information.
One and the same message can carry a lot of information for one person and not carry it at all for another person. With this approach, it is difficult to determine the amount of information unambiguously.
The alphabetical approach makes it possible to measure the information volume of a message presented in a certain language (natural or formal), regardless of its content.
To quantify any value, first of all, a unit of measurement is required. The measurement is carried out by comparing the measured value with the unit of measurement. How many times the unit of measurement "fits" in the measured value, such is the result of the measurement.
In the alphabetical approach, it is considered that each character of some message has a certain information weight - carries a fixed amount of information . All characters of the same alphabet have the same weight, depending on the cardinality of the alphabet. The information weight of a binary alphabet character is taken as the minimum unit of information and is called 1 bits.
Please note that the name of the unit of information "bit" (bit) comes from the English phrase binary digit - "binary digit".
1 bit is taken as the minimum unit of measurement of information. It is believed that this is the informational weight of the symbol of the binary alphabet.
1.6.2. Informational weight of an arbitrary alphabet character
Earlier we found out that the alphabet of any natural or formal language can be replaced by a binary alphabet. In this case, the power of the original alphabet N is related to the bit depth of the binary code i, required to encode all the characters of the original alphabet, by the relation: N = 2 i.
The information weight of the character of the alphabet i and the power of the alphabet N are related by the relation: N = 2 i.
Task 1. Pulti tribe alphabet contains 8 characters. What is the informational weight of a character in this alphabet?
Solution. Let's make a brief record of the problem statement.
There is a known relationship between i and N: N = 2 i.
Given the initial data: 8 = 2 i. Hence: i = 3.
The full solution in the notebook may look like this:
Answer: 3 bits.
1.6.3. Information volume of the message
Information volume message (the amount of information in the message), represented by the symbols of a natural or formal language, consists of the information weights of its constituent symbols.
The information volume of the message I is equal to the product of the number of characters in the message K and the information weight of the alphabet character i: I = K * i.
Task 2 . A message written in the 32-character alphabet contains 140 characters. How much information does it carry?
Task 3. An information message of 720 bits consists of 180 characters. What is the power of the alphabet with which this message is written?
1.6.4. Information units
Nowadays, the preparation of texts is mainly carried out with the help of computers. We can talk about a “computer alphabet” that includes the following characters: lowercase and uppercase Russian and Latin letters, numbers, punctuation marks, arithmetic symbols, brackets, etc. This alphabet contains 256 characters. Since 256 = 28, the information weight of each character in this alphabet is 8 bits. A value equal to eight bits is called a byte.
1 byte - informational weight of an alphabet character with a capacity of 256.
1 byte = 8 bits
Bit and byte are "small" units of measure. In practice, larger units are used to measure information volumes:
1 kilobyte = 1 KB = 1024 bytes = 210 bytes
1 megabyte = 1 MB = 1024 KB = 210 KB = 220 bytes
1 GB = 1 GB = 1024 MB = 210 MB = 220 KB = 230 bytes
1 terabyte = 1 TB = 1024 GB = 210 GB = 220 MB = 230 KB = 240 bytes
Task 4. An informational message of 4 KB consists of 4096 characters. What is the informational weight of a character in the alphabet used? How many characters are in the alphabet in which this message is written?
Task 5 . 128 athletes participate in cyclocross. A special device registers the passage by each of the participants of the intermediate finish, writing down its number as a chain of zeros and ones of the minimum length, the same for each athlete.
What will be the information volume of the message recorded by the device after 80 cyclists pass the intermediate finish line?
Solution. The numbers of the 128 participants are encoded using the binary alphabet. The required bit depth of the binary code (chain length) is 7, since 128 = 27. In other words, the message recorded by the device that one cyclist passed the intermediate finish carries 7 bits of information. When 80 athletes pass the intermediate finish, the device will record 80 7 = 560 bits, or 70 bytes of information.
A modern computer can process numerical, textual, graphic, sound and video information. All these types of information in a computer are presented in binary code, that is, only two symbols 0 and 1 are used. This is due to the fact that it is convenient to represent information in the form of a sequence of electrical impulses: there is no impulse (0), there is an impulse (1).
Such coding is usually called binary, and the logical sequences of zeros and ones themselves are called machine language.
How long does the binary code need to be in order to be able to encode your computer keyboard characters?
Thus, the information weight of one character of a sufficient alphabet is 1 byte .
To measure large volumes of information, larger units of information are used:
Units of measurement of the amount of information:
1 byte = 8 bits
1 kilobyte = 1 KB = 1024 bytes
1 megabyte = 1 MB = 1024 KB
1 GB = 1 GB = 1024 GB
Information volume of the text
1. Number of characters in the book:
60 * 40 * 150 = 360,000 characters.
2. 1 character weighs 1 byte, the information volume of the book is
360,000 bytes.
3. Convert bytes to larger units:
360,000 / 1024 = 351.56 Kb
351.56 / 1024 = 0.34 Mb
Answer: The information volume of the text is 0.34 Mb.
Task:
The information volume of the text prepared with the help of a computer is 3.
