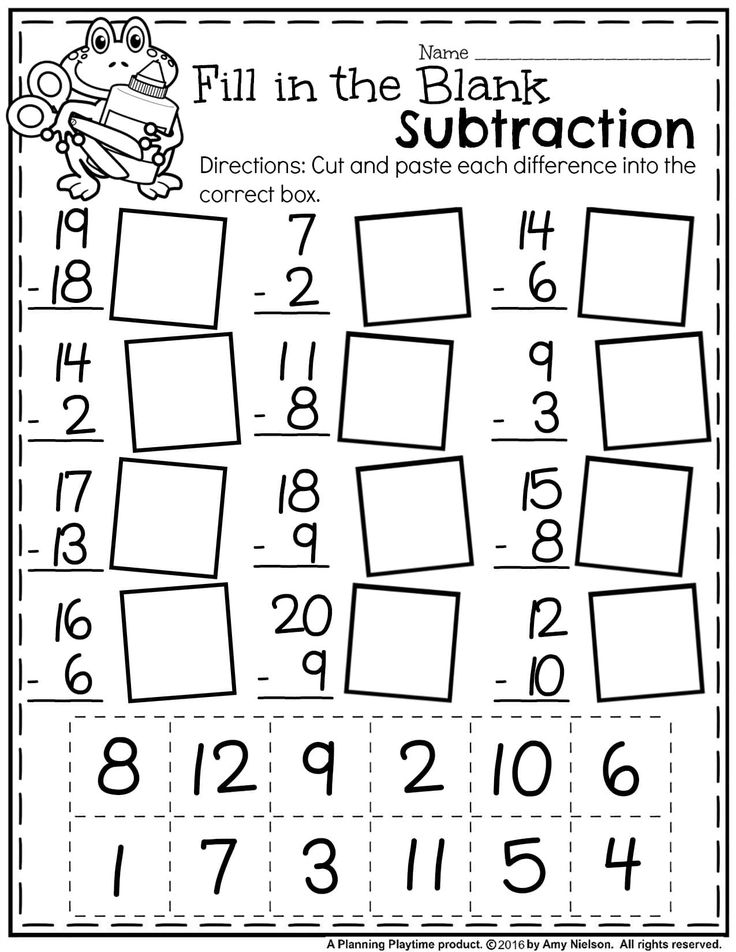
Math counting activities
30 Hands-On Counting Activities for Kids -
Skip to content
Some kids (and adults too!) have negative feelings about math. It can seem abstract and difficult. But there are lots of fun ways to make it less intimidating. Starting with the very basics, using play and activities there are lots of hands-on counting activities for kids! We’ve done so many activities to teach counting! There are way too many to list them all but here are a few of our themed favorites.
30+ Hands-On Counting Activities
More Counting Activities
Below you’ll find some of the best ideas to include counting skills within other activities like games, crafts, stories and sensory play.
Hands-On Counting Activities and GamesMath Caps: A Math Facts Game from Mosswood Connections
Get a full-year of math activities
A full-year of kindergarten math activities: perfect for small groups, partner activities and independent centers.
12 Skill Packs
20+ Activities each
Full Color
Black/white
differentiated
low-prep
click to get the kindergarten math bundleEasy Preschool Watermelon Counting Game from Homeschool Preschool
Spider Web Number Lacing Activity from Artsy Momma
Fine Motor Activity: Turkey Feather Counting from Artsy Momma
Nuts and Bolts More or Less Game from Preschool Powol Packets
Flower Counting Activity from Teaching 2 and 3 Year Olds
Counting Game for One-to-One Correspondence from Buggy and Buddy
Contact Paper Fall Tree Counting Game from Simple Fun for Kids
Felt Leaf Number Line Activity from Something 2 Offer
Foam Cup Construction with Numbers from Simple Fun for Kids
Simple Montessori Counting Activity from My Mundane and Miraculous Life
100 Items to Use to Count to 100 from Edventures with Kids
Learning to Count with Pipe Cleaners from School Time Snippets
Hands-on Preschool Counting with Rings on Fingers from School Time Snippets
Skip Counting Activities from What Do We Do All Day
Gross Motor Counting Activities
Teach Counting with a Stair Jumping Game from Homeschool Preschool
Teach Counting with Simon Says from Homeschool Preschool
Gross Motor Math Game: Counting Action Dice from Buggy and Buddy
Hands-On Crafts for Counting
Recycled K Cup Frog Craft and Counting Activity from Artsy Momma
Spider Counting Craft from Teaching 2 and 3 Year Olds
Pretend Play for Counting
Preschool Math Activity with Bear Counts from Teaching 2 and 3 Year Olds
Personalized Felt Counting Set with Ten Apples Up On Top from Buggy and Buddy
Pretend Play and Number Recognition from My Mundane and Miraculous Life
Counting 1 to 5 with 5 Little Ducks from Red Ted Art
Hands-On Sensory Activities for Counting
Exploring Numbers with Playdough from Simple Fun for Kids
Dinosaur Sensory Bin: Counting and Math from My Mundane and Miraculous Life
Our Favorite Counting Books:
We can’t live without these!
Once your child’s creativity is sparked with this fun activity, take it a step further with these engaging resources:
As an Amazon Associate I earn from qualifying purchases.
Easy Product Displays
Counting Animals on the Farm: Counting book for kids, Learn numbers from 1 to10, Counting Animals Counting Crocodiles Ten Black Dots Hand, Hand, Fingers, Thumb (Bright & Early Board Books) Curious George Learns to Count from 1 to 100 Big Book Chicka Chicka 1, 2, 3
Products here
More from our Shop
TO THE SHOP
Find even more engaging activities in the Life Over C’s shop!
With a little creativity math doesn’t have to be intimidating at all. These hands-on counting activities are sure to be a hit!
More Activities You’ll Love:
Similar Posts
Scroll to top10 Fun And Educational Counting Activities Kids Can Do At Home
Watching your child enter the wonderful world of counting activities can be equal parts amazing and overwhelming. Math is a whole language in and of itself. Learning how to read and “speak” math will take time!
Math is a whole language in and of itself. Learning how to read and “speak” math will take time!
But have no fear — HOMER is here with 10 fun, educational, and exciting counting activities to make your child’s math learning feel less like a roller coaster and more like a walk through the park.
10 Counting Activities To Try At Home
1) Count The Pattern
What You’ll Need
- A piece of paper
- A pen for tracking tallies
What To Do
This counting activity can be done inside your house on a rainy day or during a walk around the neighborhood. All you’ll need is your paper, pen, and sharp eyes.
For our example, we’ll go on a nature walk. You will start by saying, “I spy with my little eye something [color] … how many can you find?” To start, we’ll use the example of yellow objects.
Hearing your hint, your child will rush around to count how many yellow flowers, coats, signs, cars, or other objects they can find.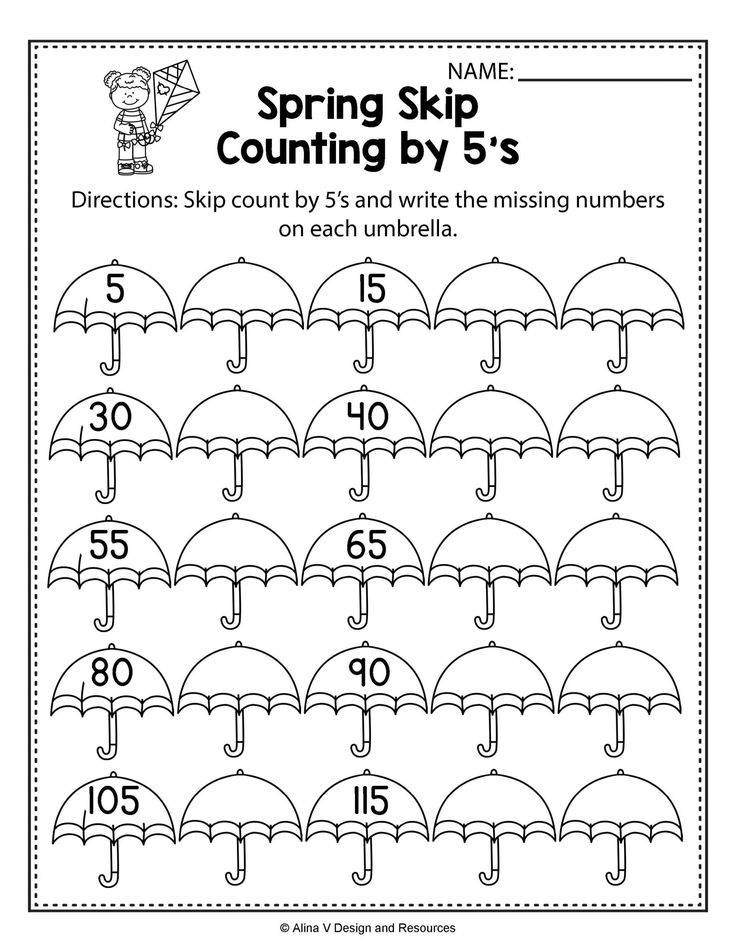
For young kids, their goal can be to find as many yellow items up to 10 as fast as they can. If your child is a little older, their goal can be 20.
You can also switch it up by exchanging the color for other objects. For example, they can try and count the number of dogs, fire hydrants, sidewalk cracks, or birds flying by.
2) Counting Cityscape
What You’ll Need
- Legos or building blocks
- A pair of dice
- Sticky notes
- Pen or marker
What To Do
For this activity, your child will start by rolling the dice.
They’ll count the dots of whatever number they roll and then stack the matching amount of building blocks into a tall tower. Then, they’ll write out the number of blocks on a sticky note and stick it to the top of their tower like a flag.
This will showcase a couple of different things to your child: one-to-one correspondence and subitizing.
Subitizing refers to a child’s ability to see a small collection of objects and innately understand how many there are without meticulously counting.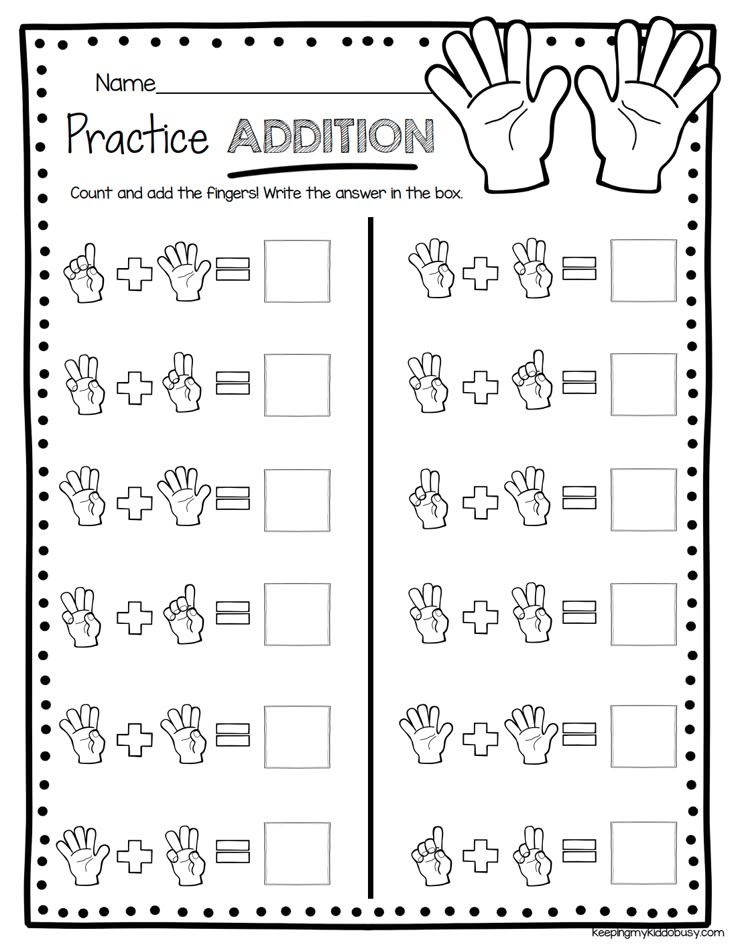 Subitizing works when reading dice as well.
Subitizing works when reading dice as well.
Encourage your child to repeat this process a few times so they begin to build their own cityscape. If all of their numbers are correct, their reward will be to play King Kong and smash it all down!
3) Ice Cream Cone Counting
What You’ll Need
- 5 triangle-shaped paper cut-outs (for the cones)
- 15 different-colored circles (for the ice cream)
- Glue or tape (if you want to preserve their work!)
- A sheet of paper with numbers 1 – 5 written across the bottom
- Leave lots of space in-between!
What To Do
The next best thing to real ice cream cones? Making your own crazy flavors out of paper!
Your child will use the number line on the paper to guide their ice cream assembly. So, for the 1 space, your child will place one ice cream cone and the number of scoops matching the spot on the number line.
They’ll continue up the number line, making ice creams with 2, 3, 4, and eventually 5 scoops. That’s one big ice cream cone! For older kids, you can bump this activity up to 10.
That’s one big ice cream cone! For older kids, you can bump this activity up to 10.
You can take this activity further by turning your ice cream making into a business! Your child can play shopkeeper and you can puppeteer different stuffed animals to come in and order.
Your child will make ice cream cones based on their fuzzy customers’ requests!
4) Penny Toss
What You’ll Need
- 10 pennies
- A plastic cup or jar (for shaking)
- A piece of paper
- A pen
What To Do
Place the pennies in your shaker jar. Tell your child to shake them all around before turning them upside down and throwing the pennies down onto the floor.
You will be playing against one another: one person for heads and one person for tails.
Then, they’ll take a tally of how many pennies land on heads vs. tails. They’ll count their tallies and circle which one got more in each round. The first person to have “their side” of the penny reach 20 wins!
5) Fill The Cup
What You’ll Need
- Popcorn or other light but bulky snack
- 2 plastic cups
- A pair of dice
What To Do
You and your child will each have your own plastic cup and a die.
You’ll start by rolling your die one person at a time. Whatever number you get, you’ll count that many pieces of popcorn into your cup. The idea is to see whose cup fills up first!
The players all get rewarded by eating their whole cup of popcorn at the end. What’s better than snacktime and math time?
6) Number Maze
What You’ll Need
- Chalk
- Sunshine (this activity is done outdoors)
- A stack of cards (face cards removed)
What To Do
You’ll use your chalk to draw out a grid. You can draw the grid in any form you like, but there should be at least 10 blocks. For more advanced counters, you can expand to 20 blocks.
When filling up the grid, you’ll want to mix and match the placement of the numbers. You don’t want to write them in an obvious sequence, as that will defeat the purpose of the game.
You will be the road map for how your child will get out of the maze. Your child must “escape” the maze by hopping between the numbers you call out.
You’ll call out numbers based on whatever card you draw from the pile. There’s no need to do all 40 cards! Start with 10 cards (all 10 numbers) and if your child really enjoys the game, then try 20.
7) Swat That Number
- What You’ll Need
- A fly swatter
- Sticky notes
- A marker
What To Do
Write numbers 1 – 10 (or more if your child is learning larger numbers) onto separate sticky notes. Stick them to a wall with a wide space in front of it so there’s room for your child to play.
Call out a number or roll a die. Whatever number is chosen, your child must swat the corresponding sticky note with the fly swatter as hard as they can.
This counting activity will get them moving, thinking, and having a blast!
8) Planting With Numbers
What You’ll Need
- 10 small cups, numbered 1 – 10
- Clear cups work best
- Seeds for a quick-growing plant
- Snap peas
- Radish
- Squash
- Soil
What To Do
Fill each cup with an appropriate amount of soil. Then, based on the number on each of the cups, your child will plant the same amount of seeds into the labeled cups until all the cups are filled.
Then, based on the number on each of the cups, your child will plant the same amount of seeds into the labeled cups until all the cups are filled.
The best part? They’ll get to watch their seeds flourish over the next couple of weeks!
They can make their own determinations about which cups grew the best. Were the seeds in the 10 cup too crowded? Were they the perfect amount? You’ll have to wait and see together!
9) Counting With PlayDoh
What You’ll Need
- PlayDoh
- Cutouts of numbers 1 – 10 (or plastic fridge magnets)
- Toothpicks (for kids four and up)
What To Do
For this activity, your child will be making some “spiky” PlayDoh hamburgers. They’ll form the PlayDoh into 10 separate patties. The color, shape, and size are up to them!
With the finished patties, they’ll press a number 1 – 10 into each patty. Then, depending on the patty’s number, they’ll add that many spikes (toothpicks) to it, continuing until all of the patties have the correct amount of toothpicks.
Bon appetit!
This activity helps your child see the relationship between the face value of a number and how many objects it represents.
Quick tip: You may want to avoid using toothpicks if your child is younger than four years old. You can use buttons or other small objects instead.
10) Number Olympics
What You’ll Need
- A pair of dice or number spinner
What To Do
This game is a great way to have your child learn and burn some energy at the same time (we know you’ll thank us later!).
You will use the number spinner or dice to roll a random number. That number will dictate how many of a certain athletic move your child will complete.
You can use any move that gets your child excited to play — jumping jacks, squats, log rolls, spins, etc.
You can even take the game outside. For example, your child could do a certain number of jumps on the trampoline or have to score a basketball goal a certain number of times.
Get creative, get jumping, and get counting!
Counting Activities For Endless Fun
We hope these counting activities sparked your imagination for ways to make math exciting and fun for your child.
As your partner in learning, we at HOMER know that there will be weeks when there’s just not enough time in the day to grow snap peas or build Lego cities. For those extra busy days in your routine, our personalized learning center is full of counting activities for your child.
Your young learner doesn’t always have to play a complex game to develop their math skills. Our Learn & Grow App will make sure that they get there (and have a blast while doing it!).
Author
Teaching preschoolers to count by means of project activities
%PDF-1.7 % 10 obj > /Metadata 4 0 R /ViewerPreferences 5 0 R >> endobj 6 0 obj /Title >> endobj 20 obj > endobj 3 0 obj > endobj 40 obj > stream
 D.1.72017-11-27T13:17:05+05:002017-11-27T13:17:05+05:00 endstream endobj 5 0 obj > endobj 70 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] /XObject> >> /MediaBox[0 0 595.
D.1.72017-11-27T13:17:05+05:002017-11-27T13:17:05+05:00 endstream endobj 5 0 obj > endobj 70 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] /XObject> >> /MediaBox[0 0 595. 32 841.92] /Contents[115 0 R 116 0 R 117 0 R] /group> /Tabs /S /StructParents 0 /Annots [118 0R] >> endobj 80 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 119 0R /group> /Tabs /S /StructParents 1 >> endobj 9 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 120 0 R /group> /Tabs /S /StructParents 2 >> endobj 10 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 121 0 R /group> /Tabs /S /StructParents 3 >> endobj 11 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 122 0 R /group> /Tabs /S /StructParents 4 >> endobj 12 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 123 0R /group> /Tabs /S /StructParents 5 >> endobj 13 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents[115 0 R 116 0 R 117 0 R] /group> /Tabs /S /StructParents 0 /Annots [118 0R] >> endobj 80 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 119 0R /group> /Tabs /S /StructParents 1 >> endobj 9 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 120 0 R /group> /Tabs /S /StructParents 2 >> endobj 10 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 121 0 R /group> /Tabs /S /StructParents 3 >> endobj 11 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 122 0 R /group> /Tabs /S /StructParents 4 >> endobj 12 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 123 0R /group> /Tabs /S /StructParents 5 >> endobj 13 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595. 32 841.92] /Contents 125 0 R /group> /Tabs /S /StructParents 6 >> endobj 14 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 128 0 R /group> /Tabs /S /StructParents 7 >> endobj 15 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 129 0 R /group> /Tabs /S /StructParents 8 >> endobj 16 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 130 0R /group> /Tabs /S /StructParents 9 >> endobj 17 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 131 0 R /group> /Tabs /S /StructParents 10 >> endobj 18 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 132 0 R /group> /Tabs /S /StructParents 11 >> endobj 19 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 133 0R /group> /Tabs /S /StructParents 14 >> endobj 20 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 125 0 R /group> /Tabs /S /StructParents 6 >> endobj 14 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 128 0 R /group> /Tabs /S /StructParents 7 >> endobj 15 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 129 0 R /group> /Tabs /S /StructParents 8 >> endobj 16 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 130 0R /group> /Tabs /S /StructParents 9 >> endobj 17 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 131 0 R /group> /Tabs /S /StructParents 10 >> endobj 18 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 132 0 R /group> /Tabs /S /StructParents 11 >> endobj 19 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 133 0R /group> /Tabs /S /StructParents 14 >> endobj 20 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 134 0R /group> /Tabs /S /StructParents 15 >> endobj 21 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 135 0 R /group> /Tabs /S /StructParents 16 >> endobj 22 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 136 0 R /group> /Tabs /S /StructParents 17 >> endobj 23 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 137 0 R /group> /Tabs /S /StructParents 18 >> endobj 24 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 138 0 R /group> /Tabs /S /StructParents 19 >> endobj 25 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 139 0 R /group> /Tabs /S /StructParents 20 >> endobj 26 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 140 0 R /group> /Tabs /S /StructParents 21 >> endobj 27 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 134 0R /group> /Tabs /S /StructParents 15 >> endobj 21 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 135 0 R /group> /Tabs /S /StructParents 16 >> endobj 22 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 136 0 R /group> /Tabs /S /StructParents 17 >> endobj 23 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 137 0 R /group> /Tabs /S /StructParents 18 >> endobj 24 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 138 0 R /group> /Tabs /S /StructParents 19 >> endobj 25 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 139 0 R /group> /Tabs /S /StructParents 20 >> endobj 26 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 140 0 R /group> /Tabs /S /StructParents 21 >> endobj 27 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 141 0 R /group> /Tabs /S /StructParents 22 >> endobj 28 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 142 0 R /group> /Tabs /S /StructParents 12 >> endobj 29 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 143 0 R /group> /Tabs /S /StructParents 23 >> endobj 30 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 144 0 R /group> /Tabs /S /StructParents 24 >> endobj 31 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 145 0 R /group> /Tabs /S /StructParents 25 >> endobj 32 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 146 0 R /group> /Tabs /S /StructParents 26 >> endobj 33 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 147 0 R /group> /Tabs /S /StructParents 27 >> endobj 34 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents 141 0 R /group> /Tabs /S /StructParents 22 >> endobj 28 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 142 0 R /group> /Tabs /S /StructParents 12 >> endobj 29 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 143 0 R /group> /Tabs /S /StructParents 23 >> endobj 30 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 144 0 R /group> /Tabs /S /StructParents 24 >> endobj 31 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 145 0 R /group> /Tabs /S /StructParents 25 >> endobj 32 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 146 0 R /group> /Tabs /S /StructParents 26 >> endobj 33 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 147 0 R /group> /Tabs /S /StructParents 27 >> endobj 34 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595. 32 841.92] /Contents 148 0R /group> /Tabs /S /StructParents 28 >> endobj 35 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 149 0R /group> /Tabs /S /StructParents 29 >> endobj 36 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 150 0 R /group> /Tabs /S /StructParents 13 >> endobj 37 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 151 0 R /group> /Tabs /S /StructParents 30 >> endobj 38 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 152 0 R /group> /Tabs /S /StructParents 31 >> endobj 39 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 153 0 R /group> /Tabs /S /StructParents 32 >> endobj 40 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 154 0 R /group> /Tabs /S /StructParents 33 >> endobj 41 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 148 0R /group> /Tabs /S /StructParents 28 >> endobj 35 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 149 0R /group> /Tabs /S /StructParents 29 >> endobj 36 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 150 0 R /group> /Tabs /S /StructParents 13 >> endobj 37 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 151 0 R /group> /Tabs /S /StructParents 30 >> endobj 38 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 152 0 R /group> /Tabs /S /StructParents 31 >> endobj 39 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 153 0 R /group> /Tabs /S /StructParents 32 >> endobj 40 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 154 0 R /group> /Tabs /S /StructParents 33 >> endobj 41 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 155 0 R /group> /Tabs /S /StructParents 34 >> endobj 42 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 156 0 R /group> /Tabs /S /StructParents 35 >> endobj 43 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 157 0 R /group> /Tabs /S /StructParents 36 >> endobj 44 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 158 0 R /group> /Tabs /S /StructParents 37 >> endobj 45 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 159 0 R /group> /Tabs /S /StructParents 38 >> endobj 46 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 160 0R /group> /Tabs /S /StructParents 39 >> endobj 47 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 161 0R /group> /Tabs /S /StructParents 40 >> endobj 48 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 155 0 R /group> /Tabs /S /StructParents 34 >> endobj 42 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 156 0 R /group> /Tabs /S /StructParents 35 >> endobj 43 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 157 0 R /group> /Tabs /S /StructParents 36 >> endobj 44 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 158 0 R /group> /Tabs /S /StructParents 37 >> endobj 45 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 159 0 R /group> /Tabs /S /StructParents 38 >> endobj 46 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 160 0R /group> /Tabs /S /StructParents 39 >> endobj 47 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 161 0R /group> /Tabs /S /StructParents 40 >> endobj 48 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 162 0 R /group> /Tabs /S /StructParents 41 >> endobj 49 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 163 0R /group> /Tabs /S /StructParents 42 >> endobj 50 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 164 0 R /group> /Tabs /S /StructParents 43 >> endobj 51 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 165 0 R /group> /Tabs /S /StructParents 44 >> endobj 52 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 166 0 R /group> /Tabs /S /StructParents 45 >> endobj 53 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 167 0 R /group> /Tabs /S /StructParents 46 >> endobj 54 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.
32 841.92] /Contents 162 0 R /group> /Tabs /S /StructParents 41 >> endobj 49 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 163 0R /group> /Tabs /S /StructParents 42 >> endobj 50 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 164 0 R /group> /Tabs /S /StructParents 43 >> endobj 51 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 165 0 R /group> /Tabs /S /StructParents 44 >> endobj 52 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 166 0 R /group> /Tabs /S /StructParents 45 >> endobj 53 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 167 0 R /group> /Tabs /S /StructParents 46 >> endobj 54 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841. 92] /Contents 169 0 R /group> /Tabs /S /StructParents 47 >> endobj 55 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 171 0 R /group> /Tabs /S /StructParents 48 >> endobj 56 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 172 0R /group> /Tabs /S /StructParents 49 >> endobj 57 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 173 0 R /group> /Tabs /S /StructParents 50 >> endobj 58 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 174 0 R /group> /Tabs /S /StructParents 51 >> endobj 59 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 175 0R /group> /Tabs /S /StructParents 52 >> endobj 60 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 176 0R /group> /Tabs /S /StructParents 53 >> endobj 61 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 841.
92] /Contents 169 0 R /group> /Tabs /S /StructParents 47 >> endobj 55 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 171 0 R /group> /Tabs /S /StructParents 48 >> endobj 56 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 172 0R /group> /Tabs /S /StructParents 49 >> endobj 57 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 173 0 R /group> /Tabs /S /StructParents 50 >> endobj 58 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 174 0 R /group> /Tabs /S /StructParents 51 >> endobj 59 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 175 0R /group> /Tabs /S /StructParents 52 >> endobj 60 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 176 0R /group> /Tabs /S /StructParents 53 >> endobj 61 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 841. 92 595.32] /Contents 177 0 R /group> /Tabs /S /StructParents 54 >> endobj 62 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 178 0R /group> /Tabs /S /StructParents 55 >> endobj 63 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 179 0 R /group> /Tabs /S /StructParents 56 >> endobj 64 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 841.92 595.32] /Contents 180 0 R /group> /Tabs /S /StructParents 57 >> endobj 65 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 181 0 R /group> /Tabs /S /StructParents 58 >> endobj 66 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 182 0R /group> /Tabs /S /StructParents 59 >> endobj 67 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 183 0 R /group> /Tabs /S /StructParents 60 >> endobj 68 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
92 595.32] /Contents 177 0 R /group> /Tabs /S /StructParents 54 >> endobj 62 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 178 0R /group> /Tabs /S /StructParents 55 >> endobj 63 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 179 0 R /group> /Tabs /S /StructParents 56 >> endobj 64 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 841.92 595.32] /Contents 180 0 R /group> /Tabs /S /StructParents 57 >> endobj 65 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 181 0 R /group> /Tabs /S /StructParents 58 >> endobj 66 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 182 0R /group> /Tabs /S /StructParents 59 >> endobj 67 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 183 0 R /group> /Tabs /S /StructParents 60 >> endobj 68 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 185 0R /group> /Tabs /S /StructParents 61 >> endobj 69 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 187 0R /group> /Tabs /S /StructParents 62 >> endobj 70 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 188 0 R /group> /Tabs /S /StructParents 63 >> endobj 71 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 189 0 R /group> /Tabs /S /StructParents 64 >> endobj 72 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 190 0 R /group> /Tabs /S /StructParents 65 >> endobj 73 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 191 0 R /group> /Tabs /S /StructParents 66 >> endobj 74 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.
32 841.92] /Contents 185 0R /group> /Tabs /S /StructParents 61 >> endobj 69 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 187 0R /group> /Tabs /S /StructParents 62 >> endobj 70 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 188 0 R /group> /Tabs /S /StructParents 63 >> endobj 71 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 189 0 R /group> /Tabs /S /StructParents 64 >> endobj 72 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 190 0 R /group> /Tabs /S /StructParents 65 >> endobj 73 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 191 0 R /group> /Tabs /S /StructParents 66 >> endobj 74 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841. 92] /Contents 192 0R /group> /Tabs /S /StructParents 67 >> endobj 75 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [193 0 R 194 0 R] /MediaBox [0 0 595.32 841.92] /Contents 195 0 R /group> /Tabs /S /StructParents 68 >> endobj 76 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /annotations[196 0 R 197 0 R 198 0 R 199 0 R 200 0 R 201 0 R 202 0 R] /MediaBox [0 0 595.32 841.92] /Contents 203 0R /group> /Tabs /S /StructParents 71 >> endobj 77 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [204 0 R] /MediaBox [0 0 595.32 841.92] /Contents 205 0 R /group> /Tabs /S /StructParents 79 >> endobj 78 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [207 0R] /MediaBox [0 0 595.32 841.92] /Contents 208 0R /group> /Tabs /S /StructParents 81 >> endobj 790 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 209 0 R /group> /Tabs /S /StructParents 83 >> endobj 80 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
92] /Contents 192 0R /group> /Tabs /S /StructParents 67 >> endobj 75 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [193 0 R 194 0 R] /MediaBox [0 0 595.32 841.92] /Contents 195 0 R /group> /Tabs /S /StructParents 68 >> endobj 76 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /annotations[196 0 R 197 0 R 198 0 R 199 0 R 200 0 R 201 0 R 202 0 R] /MediaBox [0 0 595.32 841.92] /Contents 203 0R /group> /Tabs /S /StructParents 71 >> endobj 77 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [204 0 R] /MediaBox [0 0 595.32 841.92] /Contents 205 0 R /group> /Tabs /S /StructParents 79 >> endobj 78 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [207 0R] /MediaBox [0 0 595.32 841.92] /Contents 208 0R /group> /Tabs /S /StructParents 81 >> endobj 790 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 209 0 R /group> /Tabs /S /StructParents 83 >> endobj 80 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 210 0R /group> /Tabs /S /StructParents 84 >> endobj 81 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 211 0R /group> /Tabs /S /StructParents 85 >> endobj 82 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 212 0 R /group> /Tabs /S /StructParents 86 >> endobj 83 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 213 0 R /group> /Tabs /S /StructParents 87 >> endobj 84 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 214 0 R /group> /Tabs /S /StructParents 88 >> endobj 85 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 215 0 R /group> /Tabs /S /StructParents 89 >> endobj 86 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 216 0 R /group> /Tabs /S /StructParents 90 >> endobj 87 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 210 0R /group> /Tabs /S /StructParents 84 >> endobj 81 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 211 0R /group> /Tabs /S /StructParents 85 >> endobj 82 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 212 0 R /group> /Tabs /S /StructParents 86 >> endobj 83 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 213 0 R /group> /Tabs /S /StructParents 87 >> endobj 84 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 214 0 R /group> /Tabs /S /StructParents 88 >> endobj 85 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 215 0 R /group> /Tabs /S /StructParents 89 >> endobj 86 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 216 0 R /group> /Tabs /S /StructParents 90 >> endobj 87 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 217 0 R /group> /Tabs /S /StructParents 91 >> endobj 88 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 218 0R /group> /Tabs /S /StructParents 92 >> endobj 89 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 219 0R /group> /Tabs /S /StructParents 93 >> endobj 90 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 220 0R /group> /Tabs /S /StructParents 94 >> endobj 91 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 221 0R /group> /Tabs /S /StructParents 95 >> endobj 92 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 222 0 R /group> /Tabs /S /StructParents 96 >> endobj 93 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 223 0R /group> /Tabs /S /StructParents 97 >> endobj 94 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents 217 0 R /group> /Tabs /S /StructParents 91 >> endobj 88 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 218 0R /group> /Tabs /S /StructParents 92 >> endobj 89 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 219 0R /group> /Tabs /S /StructParents 93 >> endobj 90 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 220 0R /group> /Tabs /S /StructParents 94 >> endobj 91 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 221 0R /group> /Tabs /S /StructParents 95 >> endobj 92 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 222 0 R /group> /Tabs /S /StructParents 96 >> endobj 93 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 223 0R /group> /Tabs /S /StructParents 97 >> endobj 94 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595. 32 841.92] /Contents 224 0 R /group> /Tabs /S /StructParents 98 >> endobj 95 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 225 0 R /group> /Tabs /S /StructParents 99 >> endobj 96 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 226 0 R /group> /Tabs /S /StructParents 100 >> endobj 97 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 227 0 R /group> /Tabs /S /StructParents 101 >> endobj 98 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 228 0 R /group> /Tabs /S /StructParents 102 >> endobj 99 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 230 0R /group> /Tabs /S /StructParents 103 >> endobj 100 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents 224 0 R /group> /Tabs /S /StructParents 98 >> endobj 95 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 225 0 R /group> /Tabs /S /StructParents 99 >> endobj 96 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 226 0 R /group> /Tabs /S /StructParents 100 >> endobj 97 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 227 0 R /group> /Tabs /S /StructParents 101 >> endobj 98 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 228 0 R /group> /Tabs /S /StructParents 102 >> endobj 99 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 230 0R /group> /Tabs /S /StructParents 103 >> endobj 100 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595. 32 841.92] /Contents 232 0 R /group> /Tabs /S /StructParents 104 >> endobj 101 0 obj > endobj 102 0 obj > endobj 103 0 obj > endobj 104 0 obj > endobj 105 0 obj > endobj 106 0 obj > endobj 107 0 obj > endobj 108 0 obj > endobj 109 0 obj > endobj 110 0 obj > endobj 111 0 obj > endobj 112 0 obj > endobj 113 0 obj > endobj 114 0 obj > stream x
32 841.92] /Contents 232 0 R /group> /Tabs /S /StructParents 104 >> endobj 101 0 obj > endobj 102 0 obj > endobj 103 0 obj > endobj 104 0 obj > endobj 105 0 obj > endobj 106 0 obj > endobj 107 0 obj > endobj 108 0 obj > endobj 109 0 obj > endobj 110 0 obj > endobj 111 0 obj > endobj 112 0 obj > endobj 113 0 obj > endobj 114 0 obj > stream x 


 When they say: "the set of all objects that have the property P", they mean those and only those objects that have this property.
When they say: "the set of all objects that have the property P", they mean those and only those objects that have this property. 
 The word “digit” without specification usually means one of the following ten characters: 0 1 2 3 4 5 6 7 8 9 (so-called “Arabic numerals”). Combinations of these numbers generate two (or more) digit numbers.
The word “digit” without specification usually means one of the following ten characters: 0 1 2 3 4 5 6 7 8 9 (so-called “Arabic numerals”). Combinations of these numbers generate two (or more) digit numbers.  The study of numerals and sets of objects leads to the assimilation of counting activities.
The study of numerals and sets of objects leads to the assimilation of counting activities.  The value is a property of an object perceived by various analyzers: visual, tactile and motor. In this case, the size of an object is most often perceived simultaneously by several analyzers: visual-motor, tactile-motor, etc.
The value is a property of an object perceived by various analyzers: visual, tactile and motor. In this case, the size of an object is most often perceived simultaneously by several analyzers: visual-motor, tactile-motor, etc.  So, for example, in the figure, objects are located in a vertical position and are characterized as high and low, , and in another figure (in a horizontal position), these same objects are characterized as long and short.
So, for example, in the figure, objects are located in a vertical position and are characterized as high and low, , and in another figure (in a horizontal position), these same objects are characterized as long and short. 
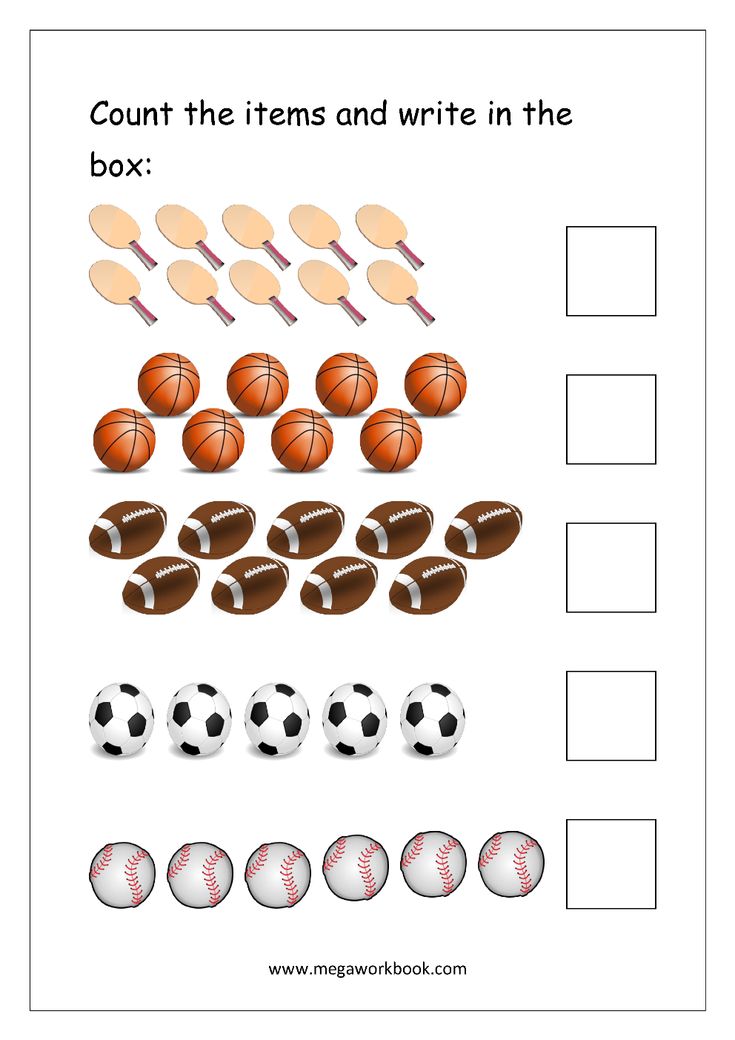


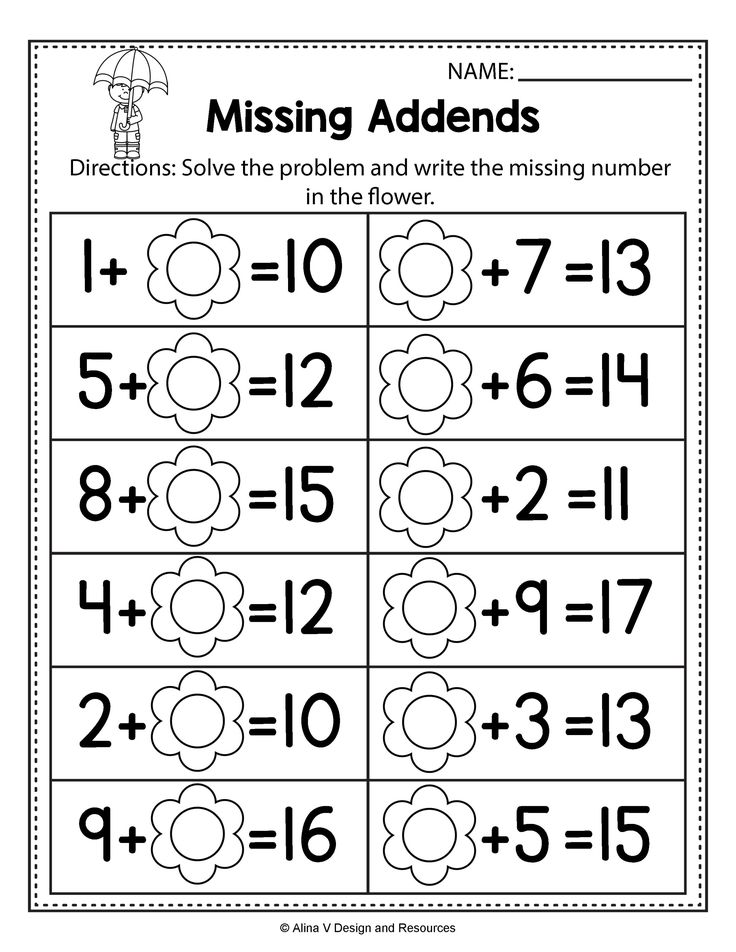


 Various counting rhymes, proverbs, sayings, riddles, nursery rhymes were good material in teaching children to count, they made it possible for the child to form concepts about numbers, shape, size, space.
Various counting rhymes, proverbs, sayings, riddles, nursery rhymes were good material in teaching children to count, they made it possible for the child to form concepts about numbers, shape, size, space. 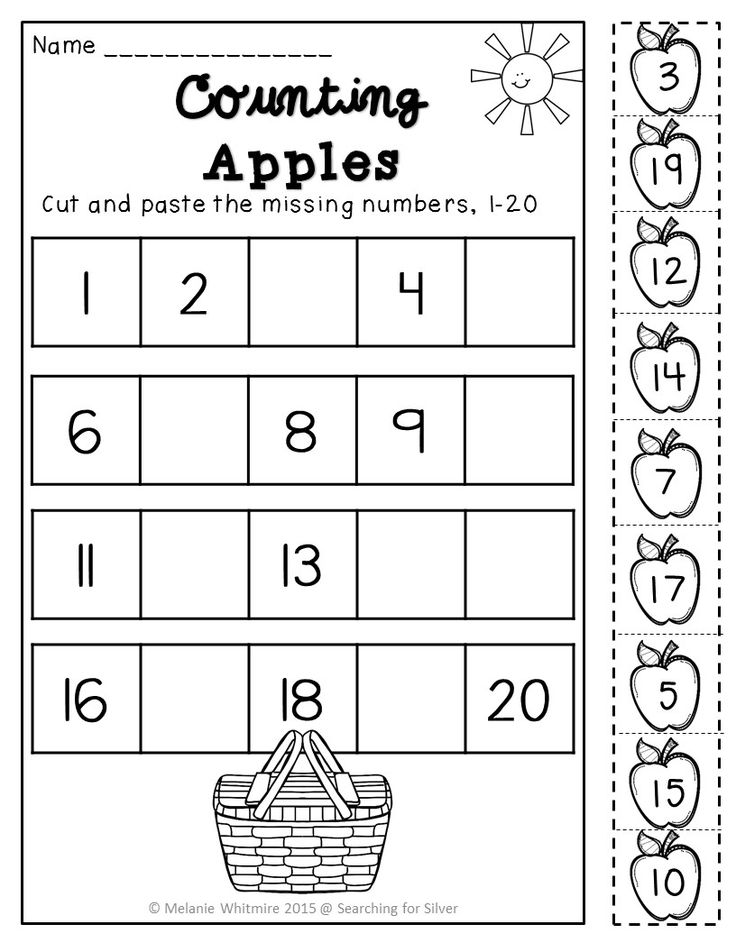 A. Comenius, M.G. Pestalozzi, K.D. Ushinsky, L.N. Tolstoy and others.
A. Comenius, M.G. Pestalozzi, K.D. Ushinsky, L.N. Tolstoy and others. 
 However, all this was just wishes, without any scientific justification.
However, all this was just wishes, without any scientific justification.  He created the famous "Gifts" - a special manual for the development of constructive skills in unity with the knowledge of numbers, shapes, sizes, spatial relationships. F. Fröbel was convinced that the development of "spatial" imagination and thinking at preschool age creates the conditions for the transition to the assimilation of geometry at school. The "gifts" created by F. Fröbel are still being used as didactic material to familiarize children with number, shape, size and spatial relationships.
He created the famous "Gifts" - a special manual for the development of constructive skills in unity with the knowledge of numbers, shapes, sizes, spatial relationships. F. Fröbel was convinced that the development of "spatial" imagination and thinking at preschool age creates the conditions for the transition to the assimilation of geometry at school. The "gifts" created by F. Fröbel are still being used as didactic material to familiarize children with number, shape, size and spatial relationships.  The M. Montessori system provides for the development of the child's sensorimotor sphere and, in the future, intellect. The "golden" mathematical material, which is especially distinguished by its significance, is first mastered by the child as a set of beads in different quantities, then in symbols (numbers), after that - as a means of mastering the ability to compare numbers. Thus, the decimal number system is presented to the child visibly and tangibly, which leads to the successful mastery of arithmetic.
The M. Montessori system provides for the development of the child's sensorimotor sphere and, in the future, intellect. The "golden" mathematical material, which is especially distinguished by its significance, is first mastered by the child as a set of beads in different quantities, then in symbols (numbers), after that - as a means of mastering the ability to compare numbers. Thus, the decimal number system is presented to the child visibly and tangibly, which leads to the successful mastery of arithmetic.  , from the concrete to the abstract), which made mathematics attractive and accessible even for 3-4-year-old children.
, from the concrete to the abstract), which made mathematics attractive and accessible even for 3-4-year-old children. 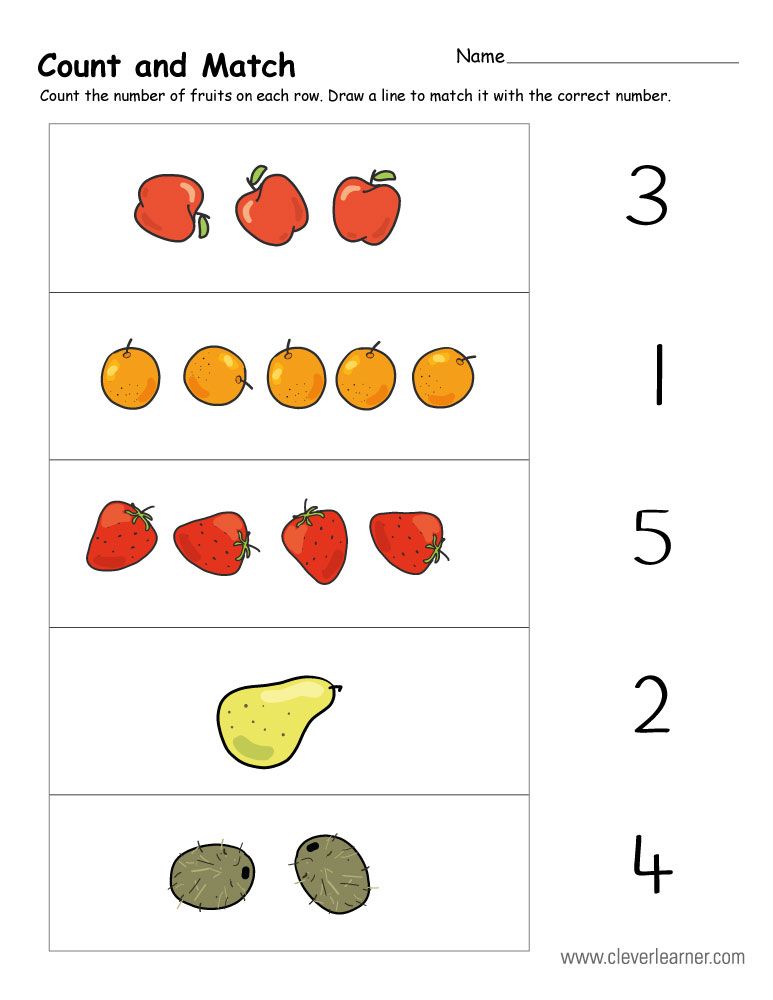 The experience of practical workers was not always scientifically substantiated, but it was tested in practice. Over time, he improved, stronger and more fully revealed progressive pedagogical thought.
The experience of practical workers was not always scientifically substantiated, but it was tested in practice. Over time, he improved, stronger and more fully revealed progressive pedagogical thought.